DOCSLIB.ORG

Chapter 14 Analog Filters

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter 14 Analog Filters Chapter 14 Analog Filters ¾ 14.1 General Considerations ¾ 14.2 First-Order Filters ¾ 14.3 Second-Order Filters ¾ 14.4 Active Filters ¾ 14.5 Approximation of Filter Response 1 Outline of the Chapter CH 14 Analog Filters 2 Why We Need Filters ¾ In order to eliminate the unwanted interference that accompanies a signal, a filter is needed. CH 14 Analog Filters 3 Filter Characteristics sufficiently narrow bad stopband attenuation attenuated amplified ¾ Ideally, a filter needs to have a flat pass band and a sharp roll- off in its transition band. ¾ Realistically, it has a rippling pass/stop band and a transition band. CH 14 Analog Filters 4 Example 14.1: Filter I Problem : Adjacent channel interference is 25 dB above the signal. Determine the required stopband attenuation if Signal to Interference ratio must exceed 15 dB. Solution: A filter with stopband attenuation of 40 dB CH 14 Analog Filters 5 Example 14.2: Filter II Problem: Adjacent 60-Hz channel interference is 40 dB above the signal. Determine the required stopband attenuation to ensure that the signal level remains 20dB above the interferer level. Solution: A high-pass filter with stopband attenuation of 60 dB at 60Hz. CH 14 Analog Filters 6 Example 14.3: Filter III ¾ A bandpass filter around 1.5 GHz is required to reject the adjacent Cellular and PCS signals. CH 14 Analog Filters 7 Classification of Filters I CH 14 Analog Filters 8 Classification of Filters II QCV121= QCV222= Continuous-time Discrete-time if VVC122> , absorbs charge from V 1 and delivers it to V2 ⇒≈a resistor CH 14 Analog Filters 9 Classification of Filters III Passive Active CH 14 Analog Filters 10 Summary of Filter Classifications CH 14 Analog Filters 11 Filter Transfer Function (a) (b) ¾ Filter (a) has a transfer function with -20dB/dec roll-off. ¾ Filter (b) has a transfer function with -40dB/dec roll-off and provides a higher selectivity. CH 14 Analog Filters 12 General Transfer Function (sz−−)( sz)( sz −) Hs()= α 12 m ()()sp−−12 sp() sp −n z = zero frequencies k = σ + jω pk = pole frequencies CH 14 Analog Filters 13 Example 14.4 : Pole-Zero Diagram 1 RC12 s+1 Cs1 Hsa ()= Hsb ()= Hsc ()= 2 R11Cs+1 RC11()1+ C 2 s+ RLCs11 1+ Ls 1+ R 1 CH 14 Analog Filters 14 Example 14.5: Position of the poles Impulse response contains exp(pkkkttjt )= exp(σ )exp(ω ) Poles on the RHP Poles on the jω axis Poles on the LHP Unstable Oscillatory Decaying (no good) (no good) (good) CH 14 Analog Filters 15 Transfer Function ()s −−zsz( ) ( sz −) Hs()= α 12 m ()()s −−psp12 () sp −n ¾ The order of the numerator m ≤ The order of the denominator n Otherwise, H(s)→∞ as s→∞. ¾ For a physically-realizable transfer function, complex zeros or poles occur in conjugate pairs. z11=+σ jω 1z21= σ − jω 1 ¾ If a zero is located on the jω axis, z1,2=± jω1 , H(s) drops to zero at ω1. 22 The numerator contains a product such as (sj−+=+ω11)( sjωω) s 1 , which vanishes at sj= ω1 CH 14 Analog Filters 16 Imaginary Zeros ¾ Imaginary zero is used to create a null at certain frequency. For this reason, imaginary zeros are placed only in the stop band. CH 14 Analog Filters 17 Sensitivity P=Filter Parameter P dP dC SC = P C C=Component Value Example: In simple RC filter, the -3dB corner frequency is given by 1/(R1C1) Errors in the cut-off frequency: (a) the value of components varies with process and temperature in ICs (b) The available values of components deviate from those required by the design ¾ Sensitivity indicates the variation of a filter parameter due to variation of a component value. CH 14 Analog Filters 18 Example 14.6: Sensitivity Problem: Determine the sensitivity of ω0 with respect to R1. ω0 =1/(R1C1 ) dω0 −1 = 2 dR1 R1 C1 dω dR 0 = − 1 ω0 R1 Sω0 = −1 R1 ¾ For example, a +5% change in R1 translates to a -5% error in ω0. CH 14 Analog Filters 19 First-Order Filters sz+ Hs()= α 1 sp+ 1 ¾ First-order filters are represented by the transfer function shown above. ¾ Low/high pass filters can be realized by changing the relative positions of poles and zeros. CH 14 Analog Filters 20 Example 14.8: First-Order. Filter I V RRCs(1)+ out ()s = 211 VRRCCsRRin 12() 1+++ 2 1 2 pCCRR=−[( + ) || ]−1 z111= −/1(RC ), 11212 R2 C ω →⇒0 ω →∞⇒ 1 R + R 12 CC12+ 11 11 < > RC()() C+ C R R RC C+ C R R 11 1 2 1 2 11()() 1 2 1 2 R C > R C CR R2C2 < R1C1 CR 2 2 1 1 11+<+21 11+>+21 CR 12 CR12 CH 14 Analog Filters 21 Example 14.9: First-Order Filter II 1 −||()R2 Vout Cs2 Iin ()s = Iin 1 Vin R1 || Cs1 R RCs+1 virtual short =−211 ⋅ R122RCs+1 R2 C ω →⇒−0 ω →∞⇒− 1 R 1 C2 R2C2 < R1C1 R2C2 > R1C1 CH 14 Analog Filters 22 Second-Order Filters General transfer function αss2 + βγ+ Hs()= ω ss22++n ω Q n ωn 1 pj1,2 =− ±ωn 1 − 2Q 4Q2 ¾ Second-order filters are characterized by the “biquadratic” equation with two complex poles shown above. ¾ When Q increases, the real part decreases while the imaginary part approaches ± ωn. => the poles look very imaginary thereby bringing the circuit closer to instability. CH 14 Analog Filters 23 . Second-Order Low-Pass Filter 2 2 γ Hj()ω = 2 2 α = β = 0 22 ⎛⎞ωn ()ωn −+ωω⎜⎟ ⎝⎠Q H(ω p ) 2 Q> 2 ∂ Hj()ω 2 = 0 H(ω p ) 2 Q> ∂ω 2 γ 2 ωn 2 for Q > 2 Peak magnitude normalized to the passband magnitude: QQ/−1(4)21− CH 14 Analog Filters 24 Example 14.10: Second-Order LPF Problem: Q of a second-order LPF = 3. Estimate the magnitude and frequency of the peak in the frequency response. 2 2 γ Hj()ω = 2 2 2 22 ⎛⎞ωn ()ωωnn−+⎜⎟ ⎝⎠3 Q = 3 QQ/11/(4)− 2 ≈ 3 2 ωnn11/(2)− Q ≈ ω CH 14 Analog Filters 25 Second-Order High-Pass Filter The zero(s) must fall below the poles α s 2 Hs()= ω ss22++n ω β = γ = 0 Q n 2 Frequency of the peak: 2 for Q > ωn /−/11(2)Q 2 Peak magnitude normalized to the passband magnitude: QQ/−1(4)21− CH 14 Analog Filters 26 Second-Order Band-Pass Filter β s Hs()= α = γ = 0 22ωn ss++ωn The magnitude approaches zero Q for both sÆ0 and sÆ ∞, reaching a maximum in between CH 14 Analog Filters 27 Example 14.2: -3-dB Bandwidth Problem: Determine the -3dB bandwidth of a band-pass response. β s Hs()= ω ()ss22++n ω Q n The response reaches 1/ 2 times its peak value at -3dB βω22 β 22Q frequency = ω 2 ()()ωω222−+n ω 22ωn n Q ⎡ 11⎤ ωω1,2=+± 0 ⎢ 1 2 ⎥ ⎣⎢ 4Q 2Q ⎦⎥ ω BW = 0 Q CH 14 Analog Filters 28 LC Realization of Second-Order Filters ω0 Ls 1 1 Z01 = at ω =∞ 0 and ZLs11==()|| 2 Z10=∞ at ωω = Cs1 LC11 s + 1 1/2 ¾ An LC tank realizes two imaginary poles at ±j/(L1C1) , which 1/2 implies infinite impedance at ω=1/(L1C1) . CH 14 Analog Filters 29 Example 14.13: LC Tank 1 Ls1 ZLs11==()|| 2 Cs1 LC11 s + 1 ¾ At ω=0, the inductor acts as a short. Z0= at ω =∞ 0 and ¾ At ω=∞, the capacitor acts as a short. 1 CH 14 Analog Filters 30 RLC Realization of Second-Order Filters Ls111 RLs ZR21==|| 22 LCs11+++1 RLCs 111 Ls 1 R 1 RLs RLs ==11 11 2 11 22ωn RLC111() s++ s RLC111() s++ s ωn RC11 LC 11 Q 1 C1 ωn ==, QR1 LC11 L1 ωn 1 pj1,2 =− ±ωn 1 − 2Q 4Q 2 11 L1 =− ±j 1 − 2 2RC11 LC11 4R11C ¾ With a resistor, the poles are no longer pure imaginary which implies there will be no infinite impedance at any ω. CH 14 Analog Filters 31 Voltage Divider Using General Impedances V Z out ()s = P VZZin S+ P Low-pass High-pass Band-pass CH 14 Analog Filters 32 Low-pass Filter Implementation with Voltage Divider ZLsS = 1 →∞ as s →∞ 1 ZRsP = ||1 →0 as → ∞ Cs1 Vout R1 ()s = 2 Vin RCLs111++ Ls 1 R 1 CH 14 Analog Filters 33 Example 14.14: Frequency Peaking V out R1 ()s = 2 Vin RC111 Ls+ Ls 1+ R 1 2 2 222 Let DRRCLL=−( 1111ω ) + 1ω Voltage gain greater than unity (peaking) occurs when a solution exists for 2 dD 22 =−2(R111CL )( R 1 − RCL 111ω ) + L 1 d()ω2 11 = 0 ⇒=ω −22 >0 LC11 2RC 1 1 C 1 Thus, when QR=⋅1 > , C C 1 2R2 1 > 1 ∵ QR= 1 L1 2 1 L 1 L 1 1 peaking occurs. CH 14 Analog Filters 34 Example 14.15: Low-pass Circuit Comparison (a) (b) Good Bad ¾ The circuit (a) has a -40dB/dec roll-off at high frequency. ¾ However, the circuit (b) exhibits only a -20dB/dec roll-off since the parallel combination of L1 and R1 is dominated by R1 because L1ω→∞, thereby reduces the circuit to R1 and C1. CH 14 Analog Filters 35 High-pass Filter Implementation with Voltage Divider α s 2 ∵ Hs( )= for high pass filter ω ss22++n ω Q n V ()||Ls R LCRs2 out s ==11 111 () 1 2 V in RC111 Ls+ Ls 1+ R 1 ()||Ls11 R + Cs1 CH 14 Analog Filters 36 Band-pass Filter Implementation with Voltage Divider Zp must contain both a capacitor and an inductor so that it approaches zero as s Æ 0 or s Æ ∞ Z β s p ∵ Hs()= ω ss22++n ω Q n 1 ()||Ls V 1 Cs Ls out s ==11 () 1 2 Vin R111CLs+ Ls 1+ R 1 ()||Ls11+ R Cs1 CH 14 Analog Filters 37 Summary ¾ Analog filters prove essential in removing unwanted frequency components that may accompany a desired signal.
Load more

Recommended publications
  • Archived: Labview Digital Filter Design Toolkit User Manual
    LabVIEWTM Digital Filter Design Toolkit User Manual Digital Filter Design Toolkit User Manual February 2005 371353A-01 Support Worldwide Technical Support and Product Information ni.com National Instruments Corporate Headquarters 11500 North Mopac Expressway Austin, Texas 78759-3504 USA Tel: 512 683 0100 Worldwide Offices Australia 1800 300 800, Austria 43 0 662 45 79 90 0, Belgium 32 0 2 757 00 20, Brazil 55 11 3262 3599, Canada (Calgary) 403 274 9391, Canada (Ottawa) 613 233 5949, Canada (Québec) 450 510 3055, Canada (Toronto) 905 785 0085, Canada (Vancouver) 604 685 7530, China 86 21 6555 7838, Czech Republic 420 224 235 774, Denmark 45 45 76 26 00, Finland 385 0 9 725 725 11, France 33 0 1 48 14 24 24, Germany 49 0 89 741 31 30, India 91 80 51190000, Israel 972 0 3 6393737, Italy 39 02 413091, Japan 81 3 5472 2970, Korea 82 02 3451 3400, Malaysia 603 9131 0918, Mexico 01 800 010 0793, Netherlands 31 0 348 433 466, New Zealand 0800 553 322, Norway 47 0 66 90 76 60, Poland 48 22 3390150, Portugal 351 210 311 210, Russia 7 095 783 68 51, Singapore 65 6226 5886, Slovenia 386 3 425 4200, South Africa 27 0 11 805 8197, Spain 34 91 640 0085, Sweden 46 0 8 587 895 00, Switzerland 41 56 200 51 51, Taiwan 886 2 2528 7227, Thailand 662 992 7519, United Kingdom 44 0 1635 523545 For further support information, refer to the Technical Support and Professional Services appendix.
    [Show full text]
  • User Defined Filter Tool 5 Series/6 Series B MSO Option 5-UDFLT/6-UDFLT Application Datasheet
    User Defined Filter Tool 5 Series/6 Series B MSO Option 5-UDFLT/6-UDFLT Application Datasheet In the broad sense, any system that processes a signal can be thought Supported filter types: of as a filter. For example, an oscilloscope channel operates as a low • Low-pass pass filter where its 3 dB down point is referred to as its bandwidth. Given a waveform of any shape, a filter can be designed that can • High-pass transform it into defined shape within the context of some basic rules, • Band-pass assumptions, and limitations. • Band-stop • All-pass Digital filters have some significant advantages over analog filters. For example, the tolerance values of analog filter circuit components are • Hilbert usually large, such that high-order filters are difficult or impossible to • Differentiator implement. With digital filters, high-order filters are easily realized. Supported filter responses: 5 Series and 6 Series MSO allow users to apply filters to math waveforms through a MATH Arbitrary function. The User Defined Filter • Butterworth (UDF) tool, Option 5/6-UDFLT takes this functionality a level deeper, • Chebyshev I providing more than MATH arbitrary basic functions and adds flexibility • Chebyshev II to support standard filters and can be used for application centric filter • Elliptical designs. • Gaussian • Bessel-Thomson Select from the various Filter Types General applications of filters Low-pass filters (LPF) are used to remove background and high- frequency noise. High-pass filters (HPF) can be used to remove DC and low-frequency components. Both LPF and HPF are commonly used in high-speed serial and data communication applications.
    [Show full text]
  • Transition Bandwidth Analysis of Infinite Impulse Response Filters Sujata Prabhakar Department of Electronics and Communication UCOE Punjabi University, Patiala Dr
    Sujata Prabhakar et al./ International Journal of Computer Science & Engineering Technology (IJCSET) Transition Bandwidth Analysis of Infinite Impulse Response Filters Sujata Prabhakar Department of Electronics and Communication UCOE Punjabi University, Patiala Dr. Amandeep Singh Sappal Associate Professor Department of Electronics and Communication UCOE Punjabi University, Patiala Abstract - Infinite impulse response (IIR) is a property applying to many linear time-invariant systems. Digital filters are the common example of linear time invariant systems. Systems with this property are called IIR systems or IIR filters. These filters have infinite length of impulse response and are in contrast to finite impulse response (FIR) filters. The basic IIR filters are – Butterworth filters, Chebyshev filters and Elliptic filters. In this paper we are going to discuss some basic theory of these filters and then we will analyze the properties of these filters. Keywords – IIR filters, FIR filters, Butterworth filters, Chebyshev filters and Elliptic filters. I. INTRODUCTION Filters are electronic devices used to modify amplitude and/or phase response of a signal according to their frequency. IIR filters are used for many applications. In [1] IIR filters are used for the suppression of noise in ECG signal. In diagnosis of ECG signal, signal acquisition must be noise free. So the physicians are able to make correct diagnosis on the condition of heart. IIR filters can be used to remove noise present in ECG signal. Adaptive IIR filters [2] can also be used to control active noise. IIR filters can also be used in Image Processing Applications [3]. IIR filters can be implemented on Xilinx system [4] to enhance the computational speed of filters.
    [Show full text]
  • Frequency Filters
    Frequency Filters By Kenneth A. Kuhn rev. Dec. 27, 2000, rev. March 5, 2013 A filter in general passes a desired quantity and stops an undesired quantity. For example, a fuel filter in a car passes gasoline and stops dirt and junk. An air filter in either a car or home passes air and stops dust and dirt. A ticket collector at a theater passes those with tickets and stops those without. The filters we will focus on pass signals in a desired frequency band and reject signals in an undesired frequency band. These filters are called frequency filters. There are five basic frequency filter types: Low-pass Signals from DC to an upper cutoff frequency are passed and signals at higher frequencies are attenuated. High-pass The inverse of a low-pass filter. Signals below a specified cutoff frequency are attenuated and signals at higher frequencies are passed. No high-pass filter can have response to infinite frequency so there is an upper low-pass response region in practice that is usually not accounted for in our model. Band-pass Signals above a lower cutoff frequency and below an upper cutoff frequency are passed and signals at lower or higher frequencies are attenuated. There are two types of band-pass filters: wide-band and narrow-band. Wide-band filters are built using a cascade of a high-pass filter that cuts off at the low frequency and a low-pass filter that cuts off at the high frequency. Narrow-band filters are built using high-Q resonators at or near the center frequency.
    [Show full text]
  • Compact Microstrip Lowpass Filter with Ultrasharp Response Using a Square-Loaded Modified T-Shaped Resonator
    Turkish Journal of Electrical Engineering & Computer Sciences Turk J Elec Eng & Comp Sci (2018) 26: 1736 – 1746 http://journals.tubitak.gov.tr/elektrik/ © TÜBİTAK Research Article doi:10.3906/elk-1801-127 Compact microstrip lowpass filter with ultrasharp response using a square-loaded modified T-shaped resonator Ali PIRASTEH, Saeed ROSHANI∗, Sobhan ROSHANI Department of Electrical Engineering, Kermanshah Branch, Islamic Azad University, Kermanshah, Iran Received: 13.01.2018 • Accepted/Published Online: 06.04.2018 • Final Version: 27.07.2018 Abstract: A miniaturized lowpass filter (LPF) with ultrasharp response, good figure of merit (FOM), and simple structure is proposed. The designed structure is fabricated and measured with a 2.9 GHz cut-off frequency. The proposed LPF consists of high impedance lines that are loaded by three similar resonators and two uniform suppressing cells. The filter size is only 0.08 × 0.23 λg, which indicates small circuit size. The proposed design exhibits good features, such as an ultrasharp roll-off rate of about 1609 dB/GHz and a good FOM of 162,820. The insertion lossofthe proposed LPF is less than 0.14 dB in the passband. With these excellent obtained specifications and flat group delay, this structure can be used in wireless antennae. Key words: Microstrip, low-pass filters (LPF), sharp roll-off, resonator 1. Introduction Microstrip low-pass filters (LPFs) are important passive elements for the attenuation of unwanted signalsand noise in communication systems [1]. LPFs are widely used to suppress unwanted harmonics in active and passive devices such as power dividers, couplers [2–4], and amplifiers [5,6].
    [Show full text]
  • The Scientist and Engineer's Guide to Digital Signal Processing
    CHAPTER 14 Introduction to Digital Filters Digital filters are used for two general purposes: (1) separation of signals that have been combined, and (2) restoration of signals that have been distorted in some way. Analog (electronic) filters can be used for these same tasks; however, digital filters can achieve far superior results. The most popular digital filters are described and compared in the next seven chapters. This introductory chapter describes the parameters you want to look for when learning about each of these filters. Filter Basics Digital filters are a very important part of DSP. In fact, their extraordinary performance is one of the key reasons that DSP has become so popular. As mentioned in the introduction, filters have two uses: signal separation and signal restoration. Signal separation is needed when a signal has been contaminated with interference, noise, or other signals. For example, imagine a device for measuring the electrical activity of a baby's heart (EKG) while still in the womb. The raw signal will likely be corrupted by the breathing and heartbeat of the mother. A filter might be used to separate these signals so that they can be individually analyzed. Signal restoration is used when a signal has been distorted in some way. For example, an audio recording made with poor equipment may be filtered to better represent the sound as it actually occurred. Another example is the deblurring of an image acquired with an improperly focused lens, or a shaky camera. These problems can be attacked with either analog or digital filters. Which is better? Analog filters are cheap, fast, and have a large dynamic range in both amplitude and frequency.
    [Show full text]
  • How to Compare Your Circuit Requirements to Active-Filter Approximations by Bonnie C
    Analog Applications Journal Industrial How to compare your circuit requirements to active-filter approximations By Bonnie C. Baker WEBENCH® Senior Applications Engineer Figure 1. Example of a low-pass Butterworth filter R1 V+ C2_S1 16 kΩ U3 R2_S1 15 nF V+ C2_S2 OPA342 ++ 14 kΩ U1 R2_S2 15 nF V+ + OPA342 5.17 k U2 + C1 + Ω V – R1_S1 + OPA342 OUT 10 nF C1_S1 + 11.7 kΩ – R1_S2 10 nF C1_S1 Vsignal V– 4.7 kΩ 10 nF – V– V– R4_S1 R3_S1 5.36 kΩ R4_S2 2.49 kΩ R3_S2 5.36 kΩ 2.49 kΩ Introduction Figure 2. Generic frequency response Numerous filter approximations, such as Butterworth, of a low-pass filter Bessel, and Chebyshev, are available in popular filter soft- ware applications; however, it can be time consuming to Transition select the right option for your system. So how do you Passband Region Region focus in on what type of filter you need in your circuit? This article defines the differences between Bessel, Butterworth, Chebyshev, Linear Phase, and traditional RP Gaussian low-pass filters. A typical Butterworth low-pass A filter is shown in Figure 1. 3 dB Generic low-pass filter frequency and time response Figure 2 illustrates the frequency response of a generic A low-pass filter. In this diagram, the x-axis shows the SB frequency in hertz (Hz) and the y-axis shows the circuit gain in volts/volts (V/V) or decibels (dB). Magnitude The low-pass filter has two frequency areas of operation: the passband region and the transition region. In the pass- band region, the input signal passes through with minimum modifications.
    [Show full text]
  • 3F3 – Digital Signal Processing (DSP)
    3F3 Digital Signal Processing Section 2: Digital Filters • A filter is a device which passes some signals 'more' than others (`selectivity’), e.g. a sinewave of one frequency more than one at another frequency. • We will deal with linear time-invariant (LTI) digital filters. • Recall that a linear system is defined by the principle of linear superposition: • If the linear system's parameters (coefficients) are constant, then it is Linear Time Invariant (LTI). [Some of the the material in this section is adapted from notes byDr Punskaya, Dr Doucet and Dr Macleod] TexPoint fonts used in EMF. Read the TexPoint manual before you delete this box.: AA A 3F3 Digital Signal Processing Write the input data sequence as: And the corresponding output sequence as: x 3F3 Digital Signal Processing The linear time-invariant digital filter can then be described by the difference equation: A direct form implementation of (3.1) is: xn = unit delay b0 bM yn a1 aN 3F3 Digital Signal Processing The operations shown in the Figure above are the full set of possible linear operations: • constant delays (by any number of samples), • addition or subtraction of signal paths, • multiplication (scaling) of signal paths by constants - (incl. -1), Any other operations make the system non-linear. Matlab filter functions 3F3 Digital Signal Processing Matlab has a filter command for implementation of linear digital filters. The format is y = filter( b, a, x); where b = [b0 b1 b2 ... bM ]; a = [ 1 a1 a2 a3 ... aN ]; So to compute the first P samples of the filter’s impulse
    [Show full text]
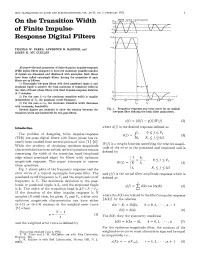
  • On the Transition Width of Finite Impulse- Response Digital Filters I 1
    IEEE TRANSACTIONS ON AUDIO AND ELECTROACOUSTICS, VOL. AU-21, NO. 1, FEBRUARY 1973 1 On the Transition Width of Finite Impulse- Response Digital Filters THOMAS W. PARKS, LAWRENCE R. RABINER, and JAMES H. MC CLELLAN Abstract-Several properties of finite-duration impulse-response (FIR) digital filters designed to have the maximum possible number of ripples are discussed and illustrated with examples. Such filters have been called extraripple filters. Among the properties of such filters are as follows. 1) Ertraripple low-pass filters with fixed passband ripple 61 and stopband ripple 62 achieve the local minimum of transition width in the class of linear phase filters with fixed impulse-response duration of N samples. 2) For the case & =62 the minimum transition width is roughly f independent of F,, the passband cutoff frequency. 3) For the case &<a1, the minimum transition width decreases FP FS with increasing bandwidth. Several figures are included to show the relation between the Fig. 1. Frequency response and error curve for anbptimal transition width and bandwidth forlow-pass filters. low-pass filter defining the basic filter parameters. Introduction The problem of designingfinite impulse-response (FIR) low-pass digital filters with linear phase has re- cently been studied from several pointsof view [1]-[6]. W(f)is a weight function specifying the relative magni- Whilethe problem of obtainingoptimum magnitude tude of the error in the passband and stopband and is characteristics has been solved, several questions remain defined by concerning the width of the transition band (stopband edgeminus passband edge) for filters with optimum magnituderesponse. This paper attempts to answer these questions.
    [Show full text]
  • Design of FIR Filters
    Design of FIR Filters Elena Punskaya www-sigproc.eng.cam.ac.uk/~op205 Some material adapted from courses by Prof. Simon Godsill, Dr. Arnaud Doucet, Dr. Malcolm Macleod and Prof. Peter Rayner 68 FIR as a class of LTI Filters Transfer function of the filter is Finite Impulse Response (FIR) Filters: N = 0, no feedback 69 FIR Filters Let us consider an FIR filter of length M (order N=M-1, watch out! order – number of delays) 70 FIR filters Can immediately obtain the impulse response, with x(n)= δ(n) δ The impulse response is of finite length M, as required Note that FIR filters have only zeros (no poles). Hence known also as all-zero filters FIR filters also known as feedforward or non-recursive, or transversal 71 FIR Filters Digital FIR filters cannot be derived from analog filters – rational analog filters cannot have a finite impulse response. Why bother? 1. They are inherently stable 2. They can be designed to have a linear phase 3. There is a great flexibility in shaping their magnitude response 4. They are easy and convenient to implement Remember very fast implementation using FFT? 72 FIR Filter using the DFT FIR filter: Now N-point DFT (Y(k)) and then N-point IDFT (y(n)) can be used to compute standard convolution product and thus to perform linear filtering (given how efficient FFT is) 73 Linear-phase filters The ability to have an exactly linear phase response is the one of the most important of FIR filters A general FIR filter does not have a linear phase response but this property is satisfied when four linear phase filter types 74 Linear-phase filters – Filter types Some observations: • Type 1 – most versatile • Type 2 – frequency response is always 0 at ω=π – not suitable as a high-pass • Type 3 and 4 – introduce a π/2 phase shift, frequency response is always 0 at ω=0 - – not suitable as a high-pass 75 FIR Design Methods • Impulse response truncation – the simplest design method, has undesirable frequency domain-characteristics, not very useful but intro to … • Windowing design method – simple and convenient but not optimal, i.e.
    [Show full text]
  • A Straightforward One-Seat Stereo Tuning Process and Some Notes About Why It Works
    A Straightforward One-Seat Stereo Tuning Process and Some Notes About Why it Works The Process Note 1: This process assumes the input to your DSP is confirmed as a flat, two-channel and in phase signal, like that of an aftermarket radio. Note 2: In an active system in which your tweeters are driven by an amplifier directly, install a capacitor in series with each tweeter to protect it from erroneous crossover settings, turn on and turn off pops and other failures that may destroy them. Choose a capacitor value that provides a -3dB point about an octave below the tweeter’s Fs. Note 3: This is not an iterative process in which you listen and then make an adjustment or two and then listen again to confirm an improvement. Once you’ve confirmed that all the speakers are connected and playing, there’s no need to listen until after all of the settings have been made and you’ve put away the RTA. Polarity, delay, crossovers, level and EQ, confirmation and additional level adjustments. That’s the order. 1. Confirm that electrical polarity is correct. Use the markings on the speakers and the amps, a polarity checker or the UMI-1 and a scope. Do not set polarity by listening for a center image from speaker pairs! 2. Put the mic in the car. 3. Measure from the center of each speaker to the microphone. Estimate a straight line from the sub to the mic no matter which way the sub is facing. If your system includes passive crossovers for the front speakers, measure to the midbass driver in a 3-way system or the midrange in a 2-way system.
    [Show full text]
  • Download the Entire Design Guide in PDF Format
    Analog and Digital Products Design/Selection Guide TABLE OF CONTENTS Pages Introduction to Frequency Devices 2 ANALOG & DIGITAL FILTER DESIGN GUIDE Analog Filter Design 3 Available Filter Technology 20 Digital Filter Design 22 Signal Reconstruction 28 Choosing a Filter Solution 29 Glossary of Terms 32 We hope the information given here will be helpful. The information is based on data and our best knowledge, and we consider the information to be true and accurate. Please read all statements, recommendations or suggestions herein in conjunction with our conditions of sale, which apply, to all goods supplied by us. We assume no responsibility for the use of these statements, recommendations or suggestions, nor do we intend them as a recommendation for any use, which would infringe any patent or copyright. 1 1784 Chessie Lane, Ottawa, IL 61350 - Tel: 800/252-7074, 815/434-7800 - FAX: 815/434-8176 e-mail: [email protected] • Web Address: http://www.freqdev.com Analog and Digital Products Filter Design Guide THE COMPANY Frequency Devices — founded in 1968 to provide electronic design engineers with analog signal solutions and engineering services — today designs and manufactures standard and custom signal conditioning, signal processing and signal analysis solutions utilizing analog, digital and integrated analog/digital technology. By addressing a wide array of signal processing needs, Frequency Devices continues to provide state-of-the-art solutions to the rapidly changing electronics industry. From prototype to production, we design and manufacture products to agreed-upon performance specifications, utilizing the latest technologies. These module, subassembly and instrument hardware and software solutions include analog and DSP (FIR and IIR) filters, instrumentation grade amplifiers, low distortion signal sources and data conversion products.
    [Show full text]