DOCSLIB.ORG

Lecture 11: Parsing Parsing Arithmetic Grammar Recursive Descent Parser

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Lecture 11: Parsing Parsing Arithmetic Grammar Recursive Descent Parser Parsing Lecture 11: Parsing • Build parse tree from an expression! CSC 131! Interested in abstract syntax tree! Fall, 2014! • ! - drops irrelevant details from parse tree Kim Bruce Arithmetic grammar Recursive Descent Parser Base recognizer (ignore building tree now) on productions:! <exp> ::= <exp> <addop> <term> ! <exp> ::= <exp> <addop> <term>! | <term> ! ! <term> ::= <term> <mulop> <factor> ! addop (fst:rest) = if fst==’+’ or fst==’-‘ then rest! | <factor> ! else error ...! <factor> ::= ( <exp> ) ! ! | NUM ! exp input = let! | ID ! inputAfterExp = exp input! <addop> ::= + | -! inputAfterAddop = addOp inputAfterExp! <mulop> ::= * | / rest = term inputAfterAddop! in ! rest or Look at parse tree & abstract syntax tree for 2 * 3 + 7 fun exp input = term(addOp(exp input)); Problems Rewrite Grammar <exp> ::= <term> <termTail> (1)! <termTail> ::= <addop> <term> <termTail> (2)! | ε (3)! <term> ::= <factor> <factorTail> (4)! <factorTail> ::= <mulop> <factor> <factorTail> (5)! • How do we select which production to use | ε (6)! when alternatives?! <factor> ::= ( <exp> ) (7)! | NUM (8)! Left-recursive - never terminates • | ID (9)! <addop> ::= + | - (10)! <mulop> ::= * | / (11) No lef recursion" How do we know which production to take? Predictive Parsing FIRST Goal: a1a2...an! • Intuition: b ∈ First(X) i% there is a derivation ! X →* bω for some ω.! S → α! 1.First(b) = b for b a terminal or the empty string! ...! 2.If have X ::= ω1 | ω2 | ... | ωn then → a1a2Xβ First(X) = First(ω1) ∪ ... ∪ First(ωn) Want next terminal character derived to be a3! 3.For any right hand side u1u2...un! ! a3 in First(γ) - First(u1) ⊆ First(u1u2...un) ! Need to apply a production X ::= γ where ! if all of u , u ..., u can derive the empty string then 1) γ can eventually derive a string starting with a3 or! - 1 2 i-1 2) If X can derive the empty string, and also ! also First(ui) ⊆ First(u1u2...un) if β can derive a string starting with a3. - empty string is in First(u1u2...un) i% all of u1, u2..., un can derive the empty string a3 in Folow(X) First for Arithmetic Follow • Intuition: A terminal b ∈ Follow(X) i% there is a FIRST(<addop>) = & +, - ' ! derivation S →* vXbω for some v and ω.! FIRST(<mulop>) = & *, / ' ! 1.If S is the start symbol then put EOF ∈ Follow(S) FIRST(<factor>) = & (, NUM, ID ' ! 2.For all rules of the form A ::= wXv,! FIRST(<term>) = & (, NUM, ID ' ! a.Add all elements of First(v) to Follow(X) FIRST(<exp>) = & (, NUM, ID ' ! If v can derive the empty string then add all elts of FIRST(<termTail>) = & +, -, ε ' ! b. Follow(A) to Follow(X)" FIRST(<factorTail>) = & *, /, ε ' • Follow(X) only used if can derive empty string from X. Follow for ArithmeticOnly needed to Predictive Parsing, redux calculate for <termTail>, Goal: a1a2...an! FOLLOW(<exp>) = & EOF, ) ' ! <factorTail> ! ! FOLLOW(<termTail>) = FOLLOW(<exp>) = & EOF, ) ' ! S → α! FOLLOW(<term>) = FIRST(<termTail>) ∪ ! ...! FOLLOW(<exp>) ∪ FOLLOW(<termTail>) ! → a1a2Xβ = & +, -, EOF, ) ' ! Want next terminal character derived to be a FOLLOW(<factorTail>) = & +, -, EOF, ) ' ! 3! ! FOLLOW(<factor>) = & *, /, +, -, EOF ( " Need to apply a production X ::= γ where ! FOLLOW(<addop>) = & (, NUM, ID ( Not needed!" 1) γ can eventually derive a string starting with a3 or! FOLLOW(<mulop>) = & (, NUM, ID ( ' 2) If X can derive the empty string, then see ! if β can derive a string starting with a3. Building Table Need Unambiguous • Put X ::= α in entry (X,a) if either! • No table entry should have more than one production to ensure it’s unambiguous, as otherwise we - a in First(α), or! don’t know which rule to apply.! - e in First(α) and a in Follow(X) • Laws of predictive parsing:! • Consequence: X ::= α in entry (X,a) i% there is - If A ::= α1 | ...| αn then for all i() j, a derivation s.t. applying production can First(αi) ∩ First(αj) = ∅. ! eventually lead to string starting with a. - If X →* ε, then First(X) ∩ Follow(X) = ∅. See ArithParse.hs Non- ID NUM Addop Mulop ( ) EOF • Laws of predictive parsing:! terminals <exp> 1 1 1 - If A ::= α1 | ...| αn then for all i() j, First(αi) ∩ First(αj) = ∅. ! <termTail> 2 3 3 - If X →* ε, then First(X) ∩ Follow(X) = ∅.! <term> 4 4 4 • 2nd is OK for arithmetic:! <factTail> 6 5 6 6 - FIRST(<termTail>) = & +, -, " ' ! ' <factor> 9 8 7 - FOLLOW(<termTail>) = & EOF, ) ' ! no overlap! <addop> 10 - FIRST(<factorTail>) = & *, /, " '! <mulop> 11 - FOLLOW(<factorTail>) = & +, -, EOF, ) ' ' Read o) fom table which production to apply! Table-Driven Stack-based Parser • http://en.wikipedia.org/wiki/LL_parser! • Start with “S $” on stack and “input $” to be recognized.! Alternatives to Recursive Descent • Use table to replace non-terminals on top of Parsers stack.! • If terminal on top of stack matches next input then erase both and proceed.! • Success if end up clearing stack and input! • Show with ID * (NUM + NUM)$ Another alternative More Options • LR(1) parsers -- bottom up, gives right-most derivation. Also stack-based.! Parser Combinators! • YACC is LR(1). ANTLR is LL(1).! • - Domain specific language for parsing.! k in LL(k) and LR(k) indicates how many • - Even easier to tie to grammar than recursive descent! letters of look ahead are necessary -- e.g. length of strings in columns of table.! - Build into Haskell and Scala, definable elsewhere! • Talk about when cover Scala • Compiler writers are happiest with k=1 to avoid exponential blow-up of table. May have to rewrite grammars..
Load more

Recommended publications
  • Syntax-Directed Translation, Parse Trees, Abstract Syntax Trees
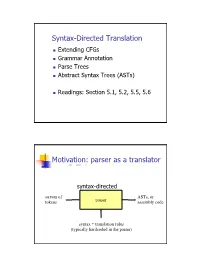
    Syntax-Directed Translation Extending CFGs Grammar Annotation Parse Trees Abstract Syntax Trees (ASTs) Readings: Section 5.1, 5.2, 5.5, 5.6 Motivation: parser as a translator syntax-directed translation stream of ASTs, or tokens parser assembly code syntax + translation rules (typically hardcoded in the parser) 1 Mechanism of syntax-directed translation syntax-directed translation is done by extending the CFG a translation rule is defined for each production given X Æ d A B c the translation of X is defined in terms of translation of nonterminals A, B values of attributes of terminals d, c constants To translate an input string: 1. Build the parse tree. 2. Working bottom-up • Use the translation rules to compute the translation of each nonterminal in the tree Result: the translation of the string is the translation of the parse tree's root nonterminal Why bottom up? a nonterminal's value may depend on the value of the symbols on the right-hand side, so translate a non-terminal node only after children translations are available 2 Example 1: arith expr to its value Syntax-directed translation: the CFG translation rules E Æ E + T E1.trans = E2.trans + T.trans E Æ T E.trans = T.trans T Æ T * F T1.trans = T2.trans * F.trans T Æ F T.trans = F.trans F Æ int F.trans = int.value F Æ ( E ) F.trans = E.trans Example 1 (cont) E (18) Input: 2 * (4 + 5) T (18) T (2) * F (9) F (2) ( E (9) ) int (2) E (4) * T (5) Annotated Parse Tree T (4) F (5) F (4) int (5) int (4) 3 Example 2: Compute type of expr E -> E + E if ((E2.trans == INT) and (E3.trans == INT) then E1.trans = INT else E1.trans = ERROR E -> E and E if ((E2.trans == BOOL) and (E3.trans == BOOL) then E1.trans = BOOL else E1.trans = ERROR E -> E == E if ((E2.trans == E3.trans) and (E2.trans != ERROR)) then E1.trans = BOOL else E1.trans = ERROR E -> true E.trans = BOOL E -> false E.trans = BOOL E -> int E.trans = INT E -> ( E ) E1.trans = E2.trans Example 2 (cont) Input: (2 + 2) == 4 1.
    [Show full text]
  • Derivatives of Parsing Expression Grammars
    Derivatives of Parsing Expression Grammars Aaron Moss Cheriton School of Computer Science University of Waterloo Waterloo, Ontario, Canada [email protected] This paper introduces a new derivative parsing algorithm for recognition of parsing expression gram- mars. Derivative parsing is shown to have a polynomial worst-case time bound, an improvement on the exponential bound of the recursive descent algorithm. This work also introduces asymptotic analysis based on inputs with a constant bound on both grammar nesting depth and number of back- tracking choices; derivative and recursive descent parsing are shown to run in linear time and constant space on this useful class of inputs, with both the theoretical bounds and the reasonability of the in- put class validated empirically. This common-case constant memory usage of derivative parsing is an improvement on the linear space required by the packrat algorithm. 1 Introduction Parsing expression grammars (PEGs) are a parsing formalism introduced by Ford [6]. Any LR(k) lan- guage can be represented as a PEG [7], but there are some non-context-free languages that may also be represented as PEGs (e.g. anbncn [7]). Unlike context-free grammars (CFGs), PEGs are unambiguous, admitting no more than one parse tree for any grammar and input. PEGs are a formalization of recursive descent parsers allowing limited backtracking and infinite lookahead; a string in the language of a PEG can be recognized in exponential time and linear space using a recursive descent algorithm, or linear time and space using the memoized packrat algorithm [6]. PEGs are formally defined and these algo- rithms outlined in Section 3.
    [Show full text]
  • A Typed, Algebraic Approach to Parsing
    A Typed, Algebraic Approach to Parsing Neelakantan R. Krishnaswami Jeremy Yallop University of Cambridge University of Cambridge United Kingdom United Kingdom [email protected] [email protected] Abstract the subject have remained remarkably stable: context-free In this paper, we recall the definition of the context-free ex- languages are specified in BackusśNaur form, and parsers pressions (or µ-regular expressions), an algebraic presenta- for these specifications are implemented using algorithms tion of the context-free languages. Then, we define a core derived from automata theory. This integration of theory and type system for the context-free expressions which gives a practice has yielded many benefits: we have linear-time algo- compositional criterion for identifying those context-free ex- rithms for parsing unambiguous grammars efficiently [Knuth pressions which can be parsed unambiguously by predictive 1965; Lewis and Stearns 1968] and with excellent error re- algorithms in the style of recursive descent or LL(1). porting for bad input strings [Jeffery 2003]. Next, we show how these typed grammar expressions can However, in languages with good support for higher-order be used to derive a parser combinator library which both functions (such as ML, Haskell, and Scala) it is very popular guarantees linear-time parsing with no backtracking and to use parser combinators [Hutton 1992] instead. These li- single-token lookahead, and which respects the natural de- braries typically build backtracking recursive descent parsers notational semantics of context-free expressions. Finally, we by composing higher-order functions. This allows building show how to exploit the type information to write a staged up parsers with the ordinary abstraction features of the version of this library, which produces dramatic increases programming language (variables, data structures and func- in performance, even outperforming code generated by the tions), which is sufficiently beneficial that these libraries are standard parser generator tool ocamlyacc.
    [Show full text]
  • Adaptive LL(*) Parsing: the Power of Dynamic Analysis
    Adaptive LL(*) Parsing: The Power of Dynamic Analysis Terence Parr Sam Harwell Kathleen Fisher University of San Francisco University of Texas at Austin Tufts University [email protected] [email protected] kfi[email protected] Abstract PEGs are unambiguous by definition but have a quirk where Despite the advances made by modern parsing strategies such rule A ! a j ab (meaning “A matches either a or ab”) can never as PEG, LL(*), GLR, and GLL, parsing is not a solved prob- match ab since PEGs choose the first alternative that matches lem. Existing approaches suffer from a number of weaknesses, a prefix of the remaining input. Nested backtracking makes de- including difficulties supporting side-effecting embedded ac- bugging PEGs difficult. tions, slow and/or unpredictable performance, and counter- Second, side-effecting programmer-supplied actions (muta- intuitive matching strategies. This paper introduces the ALL(*) tors) like print statements should be avoided in any strategy that parsing strategy that combines the simplicity, efficiency, and continuously speculates (PEG) or supports multiple interpreta- predictability of conventional top-down LL(k) parsers with the tions of the input (GLL and GLR) because such actions may power of a GLR-like mechanism to make parsing decisions. never really take place [17]. (Though DParser [24] supports The critical innovation is to move grammar analysis to parse- “final” actions when the programmer is certain a reduction is time, which lets ALL(*) handle any non-left-recursive context- part of an unambiguous final parse.) Without side effects, ac- free grammar. ALL(*) is O(n4) in theory but consistently per- tions must buffer data for all interpretations in immutable data forms linearly on grammars used in practice, outperforming structures or provide undo actions.
    [Show full text]
  • Parsing 1. Grammars and Parsing 2. Top-Down and Bottom-Up Parsing 3
    Syntax Parsing syntax: from the Greek syntaxis, meaning “setting out together or arrangement.” 1. Grammars and parsing Refers to the way words are arranged together. 2. Top-down and bottom-up parsing Why worry about syntax? 3. Chart parsers • The boy ate the frog. 4. Bottom-up chart parsing • The frog was eaten by the boy. 5. The Earley Algorithm • The frog that the boy ate died. • The boy whom the frog was eaten by died. Slide CS474–1 Slide CS474–2 Grammars and Parsing Need a grammar: a formal specification of the structures allowable in Syntactic Analysis the language. Key ideas: Need a parser: algorithm for assigning syntactic structure to an input • constituency: groups of words may behave as a single unit or phrase sentence. • grammatical relations: refer to the subject, object, indirect Sentence Parse Tree object, etc. Beavis ate the cat. S • subcategorization and dependencies: refer to certain kinds of relations between words and phrases, e.g. want can be followed by an NP VP infinitive, but find and work cannot. NAME V NP All can be modeled by various kinds of grammars that are based on ART N context-free grammars. Beavis ate the cat Slide CS474–3 Slide CS474–4 CFG example CFG’s are also called phrase-structure grammars. CFG’s Equivalent to Backus-Naur Form (BNF). A context free grammar consists of: 1. S → NP VP 5. NAME → Beavis 1. a set of non-terminal symbols N 2. VP → V NP 6. V → ate 2. a set of terminal symbols Σ (disjoint from N) 3.
    [Show full text]
  • Abstract Syntax Trees & Top-Down Parsing
    Abstract Syntax Trees & Top-Down Parsing Review of Parsing • Given a language L(G), a parser consumes a sequence of tokens s and produces a parse tree • Issues: – How do we recognize that s ∈ L(G) ? – A parse tree of s describes how s ∈ L(G) – Ambiguity: more than one parse tree (possible interpretation) for some string s – Error: no parse tree for some string s – How do we construct the parse tree? Compiler Design 1 (2011) 2 Abstract Syntax Trees • So far, a parser traces the derivation of a sequence of tokens • The rest of the compiler needs a structural representation of the program • Abstract syntax trees – Like parse trees but ignore some details – Abbreviated as AST Compiler Design 1 (2011) 3 Abstract Syntax Trees (Cont.) • Consider the grammar E → int | ( E ) | E + E • And the string 5 + (2 + 3) • After lexical analysis (a list of tokens) int5 ‘+’ ‘(‘ int2 ‘+’ int3 ‘)’ • During parsing we build a parse tree … Compiler Design 1 (2011) 4 Example of Parse Tree E • Traces the operation of the parser E + E • Captures the nesting structure • But too much info int5 ( E ) – Parentheses – Single-successor nodes + E E int 2 int3 Compiler Design 1 (2011) 5 Example of Abstract Syntax Tree PLUS PLUS 5 2 3 • Also captures the nesting structure • But abstracts from the concrete syntax a more compact and easier to use • An important data structure in a compiler Compiler Design 1 (2011) 6 Semantic Actions • This is what we’ll use to construct ASTs • Each grammar symbol may have attributes – An attribute is a property of a programming language construct
    [Show full text]
  • Efficient Recursive Parsing
    Purdue University Purdue e-Pubs Department of Computer Science Technical Reports Department of Computer Science 1976 Efficient Recursive Parsing Christoph M. Hoffmann Purdue University, [email protected] Report Number: 77-215 Hoffmann, Christoph M., "Efficient Recursive Parsing" (1976). Department of Computer Science Technical Reports. Paper 155. https://docs.lib.purdue.edu/cstech/155 This document has been made available through Purdue e-Pubs, a service of the Purdue University Libraries. Please contact [email protected] for additional information. EFFICIENT RECURSIVE PARSING Christoph M. Hoffmann Computer Science Department Purdue University West Lafayette, Indiana 47907 CSD-TR 215 December 1976 Efficient Recursive Parsing Christoph M. Hoffmann Computer Science Department Purdue University- Abstract Algorithms are developed which construct from a given LL(l) grammar a recursive descent parser with as much, recursion resolved by iteration as is possible without introducing auxiliary memory. Unlike other proposed methods in the literature designed to arrive at parsers of this kind, the algorithms do not require extensions of the notational formalism nor alter the grammar in any way. The algorithms constructing the parsers operate in 0(k«s) steps, where s is the size of the grammar, i.e. the sum of the lengths of all productions, and k is a grammar - dependent constant. A speedup of the algorithm is possible which improves the bound to 0(s) for all LL(l) grammars, and constructs smaller parsers with some auxiliary memory in form of parameters
    [Show full text]
  • Conflict Resolution in a Recursive Descent Compiler Generator
    LL(1) Conflict Resolution in a Recursive Descent Compiler Generator Albrecht Wöß, Markus Löberbauer, Hanspeter Mössenböck Johannes Kepler University Linz, Institute of Practical Computer Science, Altenbergerstr. 69, 4040 Linz, Austria {woess,loeberbauer,moessenboeck}@ssw.uni-linz.ac.at Abstract. Recursive descent parsing is restricted to languages whose grammars are LL(1), i.e., which can be parsed top-down with a single lookahead symbol. Unfortunately, many languages such as Java, C++, or C# are not LL(1). There- fore recursive descent parsing cannot be used or the parser has to make its deci- sions based on semantic information or a multi-symbol lookahead. In this paper we suggest a systematic technique for resolving LL(1) conflicts in recursive descent parsing and show how to integrate it into a compiler gen- erator (Coco/R). The idea is to evaluate user-defined boolean expressions, in order to allow the parser to make its parsing decisions where a one symbol loo- kahead does not suffice. Using our extended compiler generator we implemented a compiler front end for C# that can be used as a framework for implementing a variety of tools. 1 Introduction Recursive descent parsing [16] is a popular top-down parsing technique that is sim- ple, efficient, and convenient for integrating semantic processing. However, it re- quires the grammar of the parsed language to be LL(1), which means that the parser must always be able to select between alternatives with a single symbol lookahead. Unfortunately, many languages such as Java, C++ or C# are not LL(1) so that one either has to resort to bottom-up LALR(1) parsing [5, 1], which is more powerful but less convenient for semantic processing, or the parser has to resolve the LL(1) con- flicts using semantic information or a multi-symbol lookahead.
    [Show full text]
  • A Parsing Machine for Pegs
    A Parsing Machine for PEGs ∗ Sérgio Medeiros Roberto Ierusalimschy [email protected] [email protected] Department of Computer Science PUC-Rio, Rio de Janeiro, Brazil ABSTRACT parsing approaches. The PEG formalism gives a convenient Parsing Expression Grammar (PEG) is a recognition-based syntax for describing top-down parsers for unambiguous lan- foundation for describing syntax that renewed interest in guages. The parsers it describes can parse strings in linear top-down parsing approaches. Generally, the implementa- time, despite backtracking, by using a memoizing algorithm tion of PEGs is based on a recursive-descent parser, or uses called Packrat [1]. Although Packrat has guaranteed worst- a memoization algorithm. case linear time complexity, it also has linear space com- We present a new approach for implementing PEGs, based plexity, with a rather large constant. This makes Packrat on a virtual parsing machine, which is more suitable for impractical for parsing large amounts of data. pattern matching. Each PEG has a corresponding program LPEG [7, 11] is a pattern-matching tool for Lua, a dy- that is executed by the parsing machine, and new programs namically typed scripting language [6, 8]. LPEG uses PEGs are dynamically created and composed. The virtual machine to describe patterns instead of the more popular Perl-like is embedded in a scripting language and used by a pattern- "regular expressions" (regexes). Regexes are a more ad-hoc matching tool. way of describing patterns; writing a complex regex is more We give an operational semantics of PEGs used for pat- a trial and error than a systematic process, and their per- tern matching, then describe our parsing machine and its formance is very unpredictable.
    [Show full text]
  • Compiler Construction
    UNIVERSITY OF CAMBRIDGE Compiler Construction An 18-lecture course Alan Mycroft Computer Laboratory, Cambridge University http://www.cl.cam.ac.uk/users/am/ Lent Term 2007 Compiler Construction 1 Lent Term 2007 Course Plan UNIVERSITY OF CAMBRIDGE Part A : intro/background Part B : a simple compiler for a simple language Part C : implementing harder things Compiler Construction 2 Lent Term 2007 A compiler UNIVERSITY OF CAMBRIDGE A compiler is a program which translates the source form of a program into a semantically equivalent target form. • Traditionally this was machine code or relocatable binary form, but nowadays the target form may be a virtual machine (e.g. JVM) or indeed another language such as C. • Can appear a very hard program to write. • How can one even start? • It’s just like juggling too many balls (picking instructions while determining whether this ‘+’ is part of ‘++’ or whether its right operand is just a variable or an expression ...). Compiler Construction 3 Lent Term 2007 How to even start? UNIVERSITY OF CAMBRIDGE “When finding it hard to juggle 4 balls at once, juggle them each in turn instead ...” character -token -parse -intermediate -target stream stream tree code code syn trans cg lex A multi-pass compiler does one ‘simple’ thing at once and passes its output to the next stage. These are pretty standard stages, and indeed language and (e.g. JVM) system design has co-evolved around them. Compiler Construction 4 Lent Term 2007 Compilers can be big and hard to understand UNIVERSITY OF CAMBRIDGE Compilers can be very large. In 2004 the Gnu Compiler Collection (GCC) was noted to “[consist] of about 2.1 million lines of code and has been in development for over 15 years”.
    [Show full text]
  • AST Indexing: a Near-Constant Time Solution to the Get-Descendants-By-Type Problem Samuel Livingston Kelly Dickinson College
    Dickinson College Dickinson Scholar Student Honors Theses By Year Student Honors Theses 5-18-2014 AST Indexing: A Near-Constant Time Solution to the Get-Descendants-by-Type Problem Samuel Livingston Kelly Dickinson College Follow this and additional works at: http://scholar.dickinson.edu/student_honors Part of the Software Engineering Commons Recommended Citation Kelly, Samuel Livingston, "AST Indexing: A Near-Constant Time Solution to the Get-Descendants-by-Type Problem" (2014). Dickinson College Honors Theses. Paper 147. This Honors Thesis is brought to you for free and open access by Dickinson Scholar. It has been accepted for inclusion by an authorized administrator. For more information, please contact [email protected]. AST Indexing: A Near-Constant Time Solution to the Get-Descendants-by-Type Problem by Sam Kelly Submitted in partial fulfillment of Honors Requirements for the Computer Science Major Dickinson College, 2014 Associate Professor Tim Wahls, Supervisor Associate Professor John MacCormick, Reader Part-Time Instructor Rebecca Wells, Reader April 22, 2014 The Department of Mathematics and Computer Science at Dickinson College hereby accepts this senior honors thesis by Sam Kelly, and awards departmental honors in Computer Science. Tim Wahls (Advisor) Date John MacCormick (Committee Member) Date Rebecca Wells (Committee Member) Date Richard Forrester (Department Chair) Date Department of Mathematics and Computer Science Dickinson College April 2014 ii Abstract AST Indexing: A Near-Constant Time Solution to the Get- Descendants-by-Type Problem by Sam Kelly In this paper we present two novel abstract syntax tree (AST) indexing algorithms that solve the get-descendants-by-type problem in near constant time.
    [Show full text]
  • Advanced Parsing Techniques
    Advanced Parsing Techniques Announcements ● Written Set 1 graded. ● Hard copies available for pickup right now. ● Electronic submissions: feedback returned later today. Where We Are Where We Are Parsing so Far ● We've explored five deterministic parsing algorithms: ● LL(1) ● LR(0) ● SLR(1) ● LALR(1) ● LR(1) ● These algorithms all have their limitations. ● Can we parse arbitrary context-free grammars? Why Parse Arbitrary Grammars? ● They're easier to write. ● Can leave operator precedence and associativity out of the grammar. ● No worries about shift/reduce or FIRST/FOLLOW conflicts. ● If ambiguous, can filter out invalid trees at the end. ● Generate candidate parse trees, then eliminate them when not needed. ● Practical concern for some languages. ● We need to have C and C++ compilers! Questions for Today ● How do you go about parsing ambiguous grammars efficiently? ● How do you produce all possible parse trees? ● What else can we do with a general parser? The Earley Parser Motivation: The Limits of LR ● LR parsers use shift and reduce actions to reduce the input to the start symbol. ● LR parsers cannot deterministically handle shift/reduce or reduce/reduce conflicts. ● However, they can nondeterministically handle these conflicts by guessing which option to choose. ● What if we try all options and see if any of them work? The Earley Parser ● Maintain a collection of Earley items, which are LR(0) items annotated with a start position. ● The item A → α·ω @n means we are working on recognizing A → αω, have seen α, and the start position of the item was the nth token. ● Using techniques similar to LR parsing, try to scan across the input creating these items.
    [Show full text]