DOCSLIB.ORG

Contact Modelling in the Material Point Method Msc Thesis

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Contact Modelling in the Material Point Method Msc Thesis Contact modelling in the Material Point Method MSc Thesis Ivaylo Pantev Delft University of Technology CONTACT MODELLING IN THE MATERIAL POINT METHOD MSC THESIS by Ivaylo Pantev in partial fulfillment of the requirements for the degree of Master of Science in Civil Engineering, Geo-Engineering specialisation, at the Delft University of Technology, to be defended publicly on Thursday October 27, 2016 at 16:00 PM. Student number: 4418204 Project duration: January, 2016 – October, 2016 Thesis committee: Dr P.J. Vardon, TU Delft chairman Prof. Dr M. A. Hicks, TU Delft Prof. Dr Ir. L. J. Sluys, TU Delft J.L. Gonzalez Acosta, MSc, TU Delft PREFACE The following work marks the end of my academic career to date and the start of a new chapter in life. It represents the culmination of two wonderful years in Delft, a time to never be forgotten. The topic of this thesis topic embodies a core belief held throughout my studies - never to stray from a challenge. I have consistently found tackling a difficult, broad or novel problem has been the best way to learn and improve. This thirst for knowledge influenced my decision to pursue an MSc at TU Delft, one of the finest technical universities in the world. It is my hope that such challenges will never be too far in the future and that they will provide opportunities for continuous development throughout my career. Here I would like to express my gratitude towards the graduation committee. To my supervisor, Dr Phil Vardon for always remaining positive, even when I was not. You managed to provide inspi- ration and nurture a deep interest in the topic and numerical modelling in general. I am grateful to Prof. Michael Hicks and Prof. Bert Sluys for being ever present, bringing their humbling experience and providing a critical perspective during our meetings. Not least, Leon Acosta was always avail- able for a chat, brainstorming or debugging session - our conversations made me strive to look for solutions and improve. Here I would also like to thank Noor Pruijn, for setting a stellar example with her work on related issues in MPM and exchanging ideas throughout the thesis. Credit is also due to Bin Wang who was instrumental to the MPM research in the Geo-Engineering section and the start of this project. I owe a substantial amount to my fellow graduate students and friends in Delft, for forming a tight-knit and supportive community. Being part of a truly multicultural environment has enriched us all, taught us humility and patience among many other things, creating lasting ties across the globe. For all the friendships that started here, thank you. Finally, I would like to thank my parents and family without whom none of this would have been possible. I am eternally grateful for their unconditional support, timely guidance, wisdom and for giving me the freedom to pursue my own path. This is all one could ever wish for and comprises a debt that can never be repaid. Ivaylo Pantev Delft, October 27th 2016 iii ABSTRACT In recent years, the Material Point Method has emerged as a promising alternative to the Finite Element Method for solving problems involving localised deformations, large displacements or ro- tations, fracture, contact/impact problems and others. FEM has been a staple of engineering disci- plines both in academia and industry for decades, however its shortcomings make it less suitable for certain applications in geotechnical engineering. MPM, bridges the gap between Finite Elements and meshless methods by using a reference background grid and moving material points to rep- resent the discretised material. This gives it the capacity to faithfully reproduce behaviours which would be difficult to capture without involved procedures with other presently available methods. In this work, methods of modelling contact between deformable continua were explored in the context of the Material Point Method with the goal of producing usable code applicable to geotech- nical engineering scenarios, thus supplementing the work of the Geo-Engineering section at TU Delft. A dynamic, explicit computational framework was developed in the FORTRAN programming language allowing efficient modelling of multi-body interactions using different contact conditions. The influence of decisions regarding the contact logic, definition of surface normals and variable update procedures were compared. Coupling between FEM and MPM was explored for solving problems involving regions with small and large deformations. The work presented here aims to extend the applicability of the Material Point Method to soil-structure interaction problems. In addition to the contact algorithms explored, an alternative method for material point gener- ation using Centroidal Voronoi Tessellations was explored. This allowed for improved distribution of material points over domains of generic shape, while achieving results similar to a FEM-based approach, which uses Gauss Points. Placing material points at the integration points brings the in- herent disadvantage that complex domain shapes cannot be easily discretised using a structured grid. The ability of the two methods to reproduce a uniform density field was compared and the novel approach was implemented for a contact problem - an elastic collision between two disks. Results showed a the potential of the CVT-based scheme for use in further analyses. v CONTENTS Abstract v List of Figures xi List of Tables xiii 1 Introduction 1 1.1 Problem Statement......................................2 1.1.1 Methodology.....................................2 1.1.2 Code development goals...............................3 1.2 Report Structure.......................................3 2 Background and Methodology5 2.1 The Finite Element Method.................................5 2.1.1 General Procedure..................................5 2.1.2 Convergence and Stability Criteria.........................6 2.1.3 Contact in FEM....................................7 2.2 The Material Point Method.................................8 2.2.1 Governing Equations.................................9 2.2.2 Solution Procedure.................................. 10 2.2.3 Updating Material Point Properties......................... 13 2.2.4 Implicit and Explicit Integration........................... 13 2.3 Contact in the Material Point Method........................... 14 2.3.1 Detection....................................... 14 2.3.2 Resolution....................................... 14 2.4 Coupling with FEM...................................... 15 2.5 Outstanding Issues in MPM................................. 16 2.5.1 The Explicit MPM code................................ 16 3 Contact Algorithms 17 3.1 Overview of contact algorithms............................... 17 3.1.1 Standard MPM.................................... 17 3.1.2 The Multi-Velocity Field-Based Algorithm..................... 17 3.1.3 Notable developments................................ 18 3.1.4 Other approaches................................... 20 3.2 Contact Detection...................................... 21 3.3 Contact Geometry...................................... 22 3.3.1 Point-To-Point.................................... 22 3.4 Multi Velocity Field...................................... 23 3.4.1 Procedure....................................... 23 3.4.2 Interaction with FEM domain............................ 25 3.5 Point-To-Segment...................................... 25 3.5.1 Procedure....................................... 25 3.5.2 Alternative...................................... 27 vii viii CONTENTS 3.6 The Contact Normal and Tangent.............................. 27 3.6.1 The Normal...................................... 28 3.6.2 Nodal support array................................. 28 3.6.3 Gradient of Nodal Mass............................... 29 3.6.4 Gradient of Density.................................. 29 3.6.5 Geometric Approach................................. 30 3.6.6 The Tangent...................................... 31 3.6.7 Implementation and Comparison.......................... 32 3.6.8 Domain Boundary Treatment............................ 33 4 Material Point Generation 35 4.1 Cell Subdivision....................................... 35 4.2 Tessellations......................................... 36 4.3 Comparison.......................................... 36 4.4 Application.......................................... 40 4.5 Conclusion.......................................... 41 5 Implementation and Benchmark Problems 43 5.1 Dynamic Explicit MPM Formulation............................ 43 5.1.1 Initial Stress Assignment............................... 43 5.1.2 Energy calculation.................................. 44 5.1.3 Simple Motions.................................... 44 5.1.4 Axial Vibration of a Bar................................ 44 5.2 Contact Problems...................................... 46 5.2.1 Elastic Block Collision................................ 46 5.2.2 Elastoplastic Block Collision............................. 49 5.2.3 CVT implementation................................. 49 5.2.4 Block sliding on inclined plane........................... 50 5.2.5 Interaction Between MPM and FEM Domains................... 52 6 Conclusions and Recommendations 55 6.1 General Conclusions..................................... 55 6.2 Conclusions regarding the Multi-Mesh Algorithm..................... 55 6.2.1 Distance between contacting bodies........................ 56 6.2.2 Normal calculation.................................. 56 6.2.3 Stability.......................................
Load more

Recommended publications
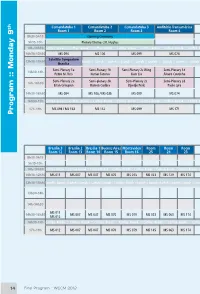
  • Program :: Monday 9
    Comandatuba 1 Comandatuba 2 Comandatuba 3 Auditório Transamérica Una Ilhéus São Paulo 3 São Paulo 2 São Paulo 1 Quito Santiago th Room 1 Room 2 Room 3 Room 4 Room 5 Room 6 Room 7 Room 8 Room 9 Room 10 Room 11 8h30-9h15 Opening Ceremony 9h15-10h Plenary Thomas J.R. Hughes 10h-10h30 Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break 10h30-12h30 MS 094 MS 106 MS 099 MS 074 MS 142 MS 133 MS 001 MS 075 MS 085 MS 002 Satellite Symposium 12h30-13h30 Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch Brasília Semi-Plenary 1a Semi-Plenary 1b Semi-Plenary 2c Wing Semi-Plenary 1d 13h30-14h Pedro M. Reis Kumar Tamma Kam Liu Álvaro Coutinho Semi-Plenary 2a Semi-plenary 2b Semi-Plenary 2c Semi-Plenary 2d 14h-14h30 Eitan Grinspun Ramon Codina Djordje Peric Paulo Lyra 14h30-16h30 MS 094 MS 106 / MS 035 MS 099 MS 074 MS 142 MS 133 MS 001 MS 075 MS 085 MS 002 16h30-17h Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break 17h-19h MS 094 / MS 163 MS 132 MS 099 MS 171 MS 142 / MS 005 MS 116 MS 001 MS 075 MS 085 MS 002 Program :: Monday 9 Brasília 3 Brasília 2 Brasília 1 Buenos Aires Montevideo Room Room Room Room Room Room Room Room
    [Show full text]
  • 14Th U.S. National Congress on Computational Mechanics
    14th U.S. National Congress on Computational Mechanics Montréal • July 17-20, 2017 Congress Program at a Glance Sunday, July 16 Monday, July 17 Tuesday, July 18 Wednesday, July 19 Thursday, July 20 Registration Registration Registration Registration Short Course 7:30 am - 5:30 pm 7:30 am - 5:30 pm 7:30 am - 5:30 pm 7:30 am - 11:30 am Registration 8:00 am - 9:30 am 8:30 am - 9:00 am OPENING PL: Tarek Zohdi PL: Andrew Stuart PL: Mark Ainsworth PL: Anthony Patera 9:00 am - 9.45 am Chair: J.T. Oden Chair: T. Hughes Chair: L. Demkowicz Chair: M. Paraschivoiu Short Courses 9:45 am - 10:15 am Coffee Break Coffee Break Coffee Break Coffee Break 9:00 am - 12:00 pm 10:15 am - 11:55 am Technical Session TS1 Technical Session TS4 Technical Session TS7 Technical Session TS10 Lunch Break 11:55 am - 1:30 pm Lunch Break Lunch Break Lunch Break CLOSING aSPL: Raúl Tempone aSPL: Ron Miller aSPL: Eldad Haber 1:30 pm - 2:15 pm bSPL: Marino Arroyo bSPL: Beth Wingate bSPL: Margot Gerritsen Short Courses 2:15 pm - 2:30 pm Break-out Break-out Break-out 1:00 pm - 4:00 pm 2:30 pm - 4:10 pm Technical Session TS2 Technical Session TS5 Technical Session TS8 4:10 pm - 4:40 pm Coffee Break Coffee Break Coffee Break Congress Registration 2:00 pm - 8:00 pm 4:40 pm - 6:20 pm Technical Session TS3 Poster Session TS6 Technical Session TS9 Reception Opening in 517BC Cocktail Coffee Breaks in 517A 7th floor Terrace Plenary Lectures (PL) in 517BC 7:00 pm - 7:30 pm Cocktail and Banquet 6:00 pm - 8:00 pm Semi-Plenary Lectures (SPL): Banquet in 517BC aSPL in 517D 7:30 pm - 9:30 pm Viewing of Fireworks bSPL in 516BC Fireworks and Closing Reception Poster Session in 517A 10:00 pm - 10:30 pm on 7th floor Terrace On behalf of Polytechnique Montréal, it is my pleasure to welcome, to Montreal, the 14th U.S.
    [Show full text]
  • An Application of the Mortar Method for Patch Coupling in NURBS-Based Isogeometric Analysis
    The weak substitution method – An application of the mortar method for patch coupling in NURBS-based isogeometric analysis W. Dornisch∗, G. Vitucci, S. Klinkel Lehrstuhl f¨urBaustatik und Baudynamik, RWTH Aachen, Mies-van-der-Rohe-Str. 1, 52074 Aachen, Germany Abstract In this contribution a mortar-type method for the coupling of non-conforming NURBS surface patches is proposed. The connection of non-conforming patches with shared degrees of freedom requires mutual refinement, which prop- agates throughout the whole patch due to the tensor-product structure of NURBS surfaces. Thus, methods to handle non-conforming meshes are essential in NURBS-based isogeometric analysis. The main objective of this work is to provide a simple and efficient way to couple the individual patches of complex geometrical models without altering the variational formulation. The deformations of the interface control points of adjacent patches are interrelated with a master-slave relation. This relation is established numerically using the weak form of the equality of mutual defor- mations along the interface. With the help of this relation the interface degrees of freedom of the slave patch can be condensated out of the system. A natural connection of the patches is attained without additional terms in the weak form. The proposed method is also applicable for nonlinear computations without further measures. Linear and ge- ometrical nonlinear examples show the high accuracy and robustness of the new method. A comparison to reference results and to computations with the Lagrange multiplier method is given. Keywords: Nonlinear isogeometric analysis, NURBS, Domain decomposition, Weak substitution method, Multi-patch connection, Mortar methods 1.
    [Show full text]
  • Analysis-Guided Improvements of the Material Point Method
    ANALYSIS-GUIDED IMPROVEMENTS OF THE MATERIAL POINT METHOD by Michael Dietel Steffen A dissertation submitted to the faculty of The University of Utah in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Computing School of Computing The University of Utah December 2009 Copyright c Michael Dietel Steffen 2009 ° All Rights Reserved THE UNIVERSITY OF UTAH GRADUATE SCHOOL SUPERVISORY COMMITTEE APPROVAL of a dissertation submitted by Michael Dietel Steffen This dissertation has been read by each member of the following supervisory committee and by majority vote has been found to be satisfactory. Chair: Robert M. Kirby Martin Berzins Christopher R. Johnson Steven G. Parker James E. Guilkey THE UNIVERSITY OF UTAH GRADUATE SCHOOL FINAL READING APPROVAL To the Graduate Council of the University of Utah: I have read the dissertation of Michael Dietel Steffen in its final form and have found that (1) its format, citations, and bibliographic style are consistent and acceptable; (2) its illustrative materials including figures, tables, and charts are in place; and (3) the final manuscript is satisfactory to the Supervisory Committee and is ready for submission to The Graduate School. Date Robert M. Kirby Chair, Supervisory Committee Approved for the Major Department Martin Berzins Chair/Dean Approved for the Graduate Council Charles A. Wight Dean of The Graduate School ABSTRACT The Material Point Method (MPM) has shown itself to be a powerful tool in the simulation of large deformation problems, especially those involving complex geometries and contact where typical finite element type methods frequently fail. While these large complex problems lead to some impressive simulations and so- lutions, there has been a lack of basic analysis characterizing the errors present in the method, even on the simplest of problems.
    [Show full text]
  • Robust Algorithms for Contact Problems with Constitutive Contact Laws
    Robust Algorithms for Contact Problems with Constitutive Contact Laws Robuste Algorithmen zur Losung¨ von Kontaktproblemen mit konstitutiven Kontaktgesetzen Der Technischen Fakultat¨ der Friedrich-Alexander-Universitat¨ Erlangen-Nurnberg¨ zur Erlangung des Doktorgrades DR.-ING. vorgelegt von Saskia Sitzmann aus Munchen¨ Als Dissertation genehmigt von der Technischen Fakultat¨ der Friedrich-Alexander-Universitat¨ Erlangen-Nurnberg¨ Tag der mundlichen¨ Prufung:¨ 27.11.2015 Vorsitzender des Promotionsorgans: Prof. Dr. Peter Greil Gutachter: Prof. Dr.-Ing. habil. Kai Willner Prof. Dr. rer.nat. habil. Barbara I. Wohlmuth Schriftenreihe Technische Mechanik Band 20 2016 · Saskia Sitzmann Robust Algorithms for Contact Problems with Constitutive Contact Laws Herausgeber: Prof. Dr.-Ing. habil. Paul Steinmann Prof. Dr.-Ing. habil. Kai Willner Erlangen 2016 Impressum Prof. Dr.-Ing. habil. Paul Steinmann Prof. Dr.-Ing. habil. Kai Willner Lehrstuhl fur¨ Technische Mechanik Universitat¨ Erlangen-Nurnberg¨ Egerlandstraße 5 91058 Erlangen Tel: +49 (0)9131 85 28502 Fax: +49 (0)9131 85 28503 ISSN 2190-023X c Saskia Sitzmann Alle Rechte, insbesondere das der Ubersetzung¨ in fremde Sprachen, vorbehalten. Ohne Genehmigung des Autors ist es nicht gestattet, dieses Heft ganz oder teilweise auf photomechanischem, elektronischem oder sonstigem Wege zu vervielfaltigen.¨ Vorwort Die vorliegende Arbeit entstand wahrend¨ meiner Tatigkeit¨ als wissenschaftliche Mitar- beiterin am Zentral Institute fur¨ Scientific Computing und dem Lehrstuhl fur¨ Technis- che Mechanik der Friedrich-Alexander-Universitat¨ Erlangen-Nurnberg¨ in Kooperation mit der MTU Aero Engines AG in Munchen.¨ Mein besonderer Dank gilt meinem Doktorvater, Herrn Prof. Kai Willner, der im- mer ein offenes Ohr fur¨ mich hatte und mich sowohl fachlich als auch mental wahrend¨ meiner gesamten Promotion bestmoglich¨ betreut hat.
    [Show full text]
  • Scalable Large-Scale Fluid-Structure Interaction Solvers in the Uintah Framework Via Hybrid Task-Based Parallelism Algorithms
    1 Scalable Large-scale Fluid-structure Interaction Solvers in the Uintah Framework via Hybrid Task-based Parallelism Algorithms Qingyu Meng, Martin Berzins UUSCI-2012-004 Scientific Computing and Imaging Institute University of Utah Salt Lake City, UT 84112 USA May 7, 2012 Abstract: Uintah is a software framework that provides an environment for solving fluid-structure interaction problems on structured adaptive grids on large-scale science and engineering problems involving the solution of partial differential equations. Uintah uses a combination of fluid-flow solvers and particle-based methods for solids, together with adaptive meshing and a novel asynchronous task-based approach with fully automated load balancing. When applying Uintah to fluid-structure interaction problems with mesh refinement, the combination of adaptive meshing and the move- ment of structures through space present a formidable challenge in terms of achieving scalability on large-scale parallel computers. With core counts per socket continuing to grow along with the prospect of less memory per core, adopting a model that uses MPI to communicate between nodes and a shared memory model on-node is one approach to achieve scalability at full machine capacity on current and emerging large-scale systems. For this approach to be successful, it is necessary to design data-structures that large numbers of cores can simultaneously access without contention. These data structures and algorithms must also be designed to avoid the overhead involved with locks and other synchronization primitives when running on large number of cores per node, as contention for acquiring locks quickly becomes untenable. This scalability challenge is addressed here for Uintah, by the development of new hybrid runtime and scheduling algorithms combined with novel lockfree data structures, making it possible for Uintah to achieve excellent scalability for a challenging fluid-structure problem with mesh refinement on as many as 260K cores.
    [Show full text]
  • Mortar Finite Element Methods for Second Order Elliptic and Parabolic Problems
    MORTAR FINITE ELEMENT METHODS FOR SECOND ORDER ELLIPTIC AND PARABOLIC PROBLEMS Thesis Submitted in partial fulfillment of the requirements For the degree of Doctor of Philosophy by Ajit Patel (02409001) Under the Supervision of Supervisor : Professor Amiya Kumar Pani Co-supervisor : Professor Neela Nataraj DEPARTMENT OF MATHEMATICS INDIAN INSTITUTE OF TECHNOLOGY, BOMBAY 2008 Approval Sheet The thesis entitled \MORTAR FINITE ELEMENT METHODS FOR SECOND ORDER ELLIPTIC AND PARABOLIC PROBLEMS" by Ajit Patel is approved for the degree of DOCTOR OF PHILOSOPHY Examiners Supervisors Chairman Date : Place : Dedicated to My Father Sri Tarachand Patel & My Mother Smt. Latika Patel INDIAN INSTITUTE OF TECHNOLOGY, BOMBAY, INDIA CERTIFICATE OF COURSE WORK This is to certify that Mr. Ajit Patel was admitted to the candidacy of the Ph.D. Degree on 18th July 2002, after successfully completing all the courses required for the Ph.D. Degree programme. The details of the course work done are given below. Sr. No. Course No. Course Name Credits 1. MA 501 Algebra II AU 2. MA 509 Elementary Number Theory 6.00 3. MA 825 Algebra 6.00 4. MA 827 Analysis 6.00 5. MA 530 Nonlinear Analysis AU 6. MA 534 Modern Theory of PDE's 6.00 7. MA 828 Functional Analysis 6.00 8. MA 838 Special Topics in Mathematics II 6.00 I. I. T. Bombay Dy. Registrar (Academic) Dated : Abstract The main objective of this thesis is to analyze mortar finite element methods for elliptic and parabolic initial-boundary value problems. In Chapter 2 of this dissertation, we have discussed a standard mortar finite element method and a mortar element method with Lagrange multiplier for spatial discretization of a class of parabolic initial-boundary value problems.
    [Show full text]
  • The Material-Point Method for Granular Materials
    Comput. Methods Appl. Mech. Engrg. 187 (2000) 529±541 www.elsevier.com/locate/cma The material-point method for granular materials S.G. Bardenhagen a, J.U. Brackbill b,*, D. Sulsky c a ESA-EA, MS P946 Los Alamos National Laboratory, Los Alamos, NM 87545, USA b T-3, MS B216 Los Alamos National Laboratory, Los Alamos, NM 87545, USA c Department of Mathematics and Statistics, University of New Mexico, Albuquerqe, NM 87131, USA Abstract A model for granular materials is presented that describes both the internal deformation of each granule and the interactions between grains. The model, which is based on the FLIP-material point, particle-in-cell method, solves continuum constitutive models for each grain. Interactions between grains are calculated with a contact algorithm that forbids interpenetration, but allows separation and sliding and rolling with friction. The particle-in-cell method eliminates the need for a separate contact detection step. The use of a common rest frame in the contact model yields a linear scaling of the computational cost with the number of grains. The properties of the model are illustrated by numerical solutions of sliding and rolling contacts, and for granular materials by a shear calculation. The results of numerical calculations demonstrate that contacts are modeled accurately for smooth granules whose shape is resolved by the computation mesh. Ó 2000 Elsevier Science S.A. All rights reserved. 1. Introduction Granular materials are large conglomerations of discrete macroscopic particles, which may slide against one another but not penetrate [9]. Like a liquid, granular materials can ¯ow to assume the shape of the container.
    [Show full text]
  • References (In Progress)
    R References (in progress) R–1 Appendix R: REFERENCES (IN PROGRESS) TABLE OF CONTENTS Page §R.1 Foreword ...................... R–3 §R.2 Reference Database .................. R–3 R–2 §R.2 REFERENCE DATABASE §R.1. Foreword Collected references for most Chapters (except those in progress) for books Advanced Finite Element Methods; master-elective and doctoral level, abbrv. AFEM Advanced Variational Methods in Mechanics; master-elective and doctoral level, abbrv. AVMM Fluid Structure Interaction; doctoral level, abbrv. FSI Introduction to Aerospace Structures; junior undergraduate level, abbrv. IAST Matrix Finite Element Methods in Statics; senior-elective and master level, abbrv. MFEMS Matrix Finite Element Methods in Dynamics; senior-elective and master level, abbrv. MFEMD Introduction to Finite Element Methods; senior-elective and master level, abbrv. IFEM Nonlinear Finite Element Methods; master-elective and doctoral level, abbrv. NFEM Margin letters are to facilitate sort; will be removed on completion. Note 1: Many books listed below are out of print. The advent of the Internet has meant that it is easier to surf for used books across the world without moving from your desk. There is a fast search “metaengine” for comparing prices at URL http://www.addall.com: click on the “search for used books” link. Amazon.com has also a search engine, which is poorly organized, confusing and full of unnecessary hype, but does link to online reviews. [Since about 2008, old scanned books posted online on Google are an additional potential source; free of charge if the useful pages happen to be displayed. Such files cannot be downloaded or printed.] Note 2.
    [Show full text]
  • And Smoothed Particle Hydrodynamics (SPH) Computational Techniques
    A strategy to couple the material point method (MPM) and smoothed particle hydrodynamics (SPH) computational techniques The MIT Faculty has made this article openly available. Please share how this access benefits you. Your story matters. Citation Raymond, Samuel J., Bruce Jones, and John R. Williams. “A Strategy to Couple the Material Point Method (MPM) and Smoothed Particle Hydrodynamics (SPH) Computational Techniques.” Computational Particle Mechanics 5, no. 1 (December 10, 2016): 49– 58. As Published http://dx.doi.org/10.1007/s40571-016-0149-9 Publisher Springer International Publishing Version Author's final manuscript Citable link http://hdl.handle.net/1721.1/116233 Terms of Use Creative Commons Attribution-Noncommercial-Share Alike Detailed Terms http://creativecommons.org/licenses/by-nc-sa/4.0/ Computational Particle Mechanics manuscript No. (will be inserted by the editor) A strategy to couple the Material Point Method (MPM) and Smoothed Particle Hydrodynamics (SPH) computational techniques Samuel J. Raymond · Bruce Jones · John R. Williams Received: date / Accepted: date Abstract A strategy is introduced to allow coupling of the Material Point Method (MPM) and Smoothed Particle Hydrodynamics (SPH) for numerical simulations. This new strategy partitions the domain into SPH and MPM regions, particles carry all state variables and as such no special treatment is required for the transition between regions. The aim of this work is to derive and validate the coupling methodology between MPM and SPH. Such coupling allows for general boundary conditions to be used in an SPH simulation without further augmentation. Additionally, as SPH is a purely particle method and MPM is a combination of particles and a mesh, this coupling also permits a smooth transition from particle methods to mesh methods.
    [Show full text]
  • Feel++ : a Computational Framework for Galerkin Methods and Advanced Numerical Methods
    ESAIM: PROCEEDINGS, December 2012, Vol. 38, p. 429-455 F. Coquel, M. Gutnic, P. Helluy, F. Lagoutiere,` C. Rohde, N. Seguin, Editors FEEL++: A COMPUTATIONAL FRAMEWORK FOR GALERKIN METHODS AND ADVANCED NUMERICAL METHODS CHRISTOPHE PRUD’HOMME 2,VINCENT CHABANNES 1,VINCENT DOYEUX 3,MOURAD ISMAIL 3,ABDOULAYE SAMAKE 1 AND GONCALO PENA 4 Abstract. This paper presents an overview of a unified framework for finite element and spectral element methods in 1D, 2D and 3D in C++ called FEEL++. The article is divided in two parts. The first part pro- vides a digression through the design of the library as well as the main abstractions handled by it, namely, meshes, function spaces, operators, linear and bilinear forms and an embedded variational language. In every case, the closeness between the language developed in FEEL++ and the equivalent mathematical ob- jects is highlighted. In the second part, examples using the mortar, Schwartz (non)overlapping, three fields and two fictitious domain-like methods (the Fat Boundary Method and the Penalty Method) are presented and numerically solved in the scope of the library. 1. INTRODUCTION Libraries to solve problems arising from partial differential equations (PDEs) through generalized Galerkin methods are a common tool among mathematicians and engineers. However, most libraries end up specializing in a type of equation, e.g. Navier-Stokes or linear elasticity models, or a specific type of numerical method, e.g. finite elements. The increasing complexity of differential models and the implementation of state of the art robust numerical methods, demand from scientific computing platforms general and clear enough languages to express such problems and provide a wealth of solution algorithms available in a minimal amount of code but maximum mathematical control.
    [Show full text]
  • A Three-Level Bddc Algorithm for Mortar Discretizations ∗
    A THREE-LEVEL BDDC ALGORITHM FOR MORTAR DISCRETIZATIONS ∗ HYEA HYUN KIM y AND XUEMIN TU z March 27, 2008 Abstract. In this paper, a three-level BDDC algorithm is developed for the solutions of large sparse algebraic linear systems arising from the mortar discretization of elliptic boundary value problems. The mortar discretization is considered on geometrically non-conforming subdomain partitions. In two-level BDDC algorithms, the coarse problem needs to be solved exactly. However, its size will increase with the increase of the number of the subdo- mains. To overcome this limitation, the three-level algorithm solves the coarse problem inexactly while a good rate of convergence is maintained. This is an extension of previous work, the three-level BDDC algorithms for standard finite element discretization. Estimates of the condition numbers are provided for the three-level BDDC method and numerical experiments are also discussed. Key words. mortar discretization, BDDC, three-level, domain decomposition, coarse problem, condition num- ber AMS subject classifications. 65N30, 65N55 1. Introduction. Mortar methods were introduced by Bernardi, Maday, and Patera [3] to couple different approximations in different subdomains so as to obtain a good global approximate solution. They are useful for modeling multi-physics, adaptivity, problems with joints, and mesh generation for three dimensional complex structures. The coupling between different subdomains in mortar methods is done by enforcing certain constraints on solutions across the subdomain interface using Lagrange multipliers. We call these constraints the mortar matching conditions. BDDC (Balancing Domain Decomposition by Constraints) methods were introduced and analyzed in [6, 16, 17] for standard finite element discretizations.
    [Show full text]