Lossless Compression with Latent Variable Models
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
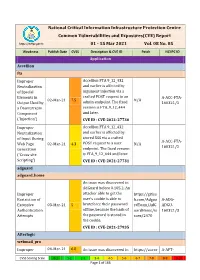
National Critical Information Infrastructure Protection Centre Common Vulnerabilities and Exposures(CVE) Report
National Critical Information Infrastructure Protection Centre Common Vulnerabilities and Exposures(CVE) Report https://nciipc.gov.in 01 - 15 Mar 2021 Vol. 08 No. 05 Weakness Publish Date CVSS Description & CVE ID Patch NCIIPC ID Application Accellion fta Improper Accellion FTA 9_12_432 Neutralization and earlier is affected by of Special argument injection via a Elements in crafted POST request to an A-ACC-FTA- 02-Mar-21 7.5 N/A Output Used by admin endpoint. The fixed 160321/1 a Downstream version is FTA_9_12_444 Component and later. ('Injection') CVE ID : CVE-2021-27730 Improper Accellion FTA 9_12_432 Neutralization and earlier is affected by of Input During stored XSS via a crafted A-ACC-FTA- Web Page 02-Mar-21 4.3 POST request to a user N/A 160321/2 Generation endpoint. The fixed version ('Cross-site is FTA_9_12_444 and later. Scripting') CVE ID : CVE-2021-27731 adguard adguard_home An issue was discovered in AdGuard before 0.105.2. An Improper attacker able to get the https://githu Restriction of user's cookie is able to b.com/Adgua A-ADG- Excessive 03-Mar-21 5 bruteforce their password rdTeam/AdG ADGU- Authentication offline, because the hash of uardHome/is 160321/3 Attempts the password is stored in sues/2470 the cookie. CVE ID : CVE-2021-27935 Afterlogic webmail_pro Improper 04-Mar-21 6.8 An issue was discovered in https://auror A-AFT- CVSS Scoring Scale 0-1 1-2 2-3 3-4 4-5 5-6 6-7 7-8 8-9 9-10 Page 1 of 166 Weakness Publish Date CVSS Description & CVE ID Patch NCIIPC ID Limitation of a AfterLogic Aurora through amail.wordpr WEBM- Pathname to a 8.5.3 and WebMail Pro ess.com/202 160321/4 Restricted through 8.5.3, when DAV is 1/02/03/add Directory enabled. -

An Improved Objective Metric to Predict Image Quality Using Deep Neural Networks
https://doi.org/10.2352/ISSN.2470-1173.2019.12.HVEI-214 © 2019, Society for Imaging Science and Technology An Improved Objective Metric to Predict Image Quality using Deep Neural Networks Pinar Akyazi and Touradj Ebrahimi; Multimedia Signal Processing Group (MMSPG); Ecole Polytechnique Fed´ erale´ de Lausanne; CH 1015, Lausanne, Switzerland Abstract ages in a full reference (FR) framework, i.e. when the reference Objective quality assessment of compressed images is very image is available, is a difference-based metric called the peak useful in many applications. In this paper we present an objec- signal to noise ratio (PSNR). PSNR and its derivatives do not tive quality metric that is better tuned to evaluate the quality of consider models based on the human visual system (HVS) and images distorted by compression artifacts. A deep convolutional therefore often result in low correlations with subjective quality neural networks is used to extract features from a reference im- ratings. [1]. Metrics such as structural similarity index (SSIM) age and its distorted version. Selected features have both spatial [2], multi-scale structural similarity index (MS-SSIM) [3], feature and spectral characteristics providing substantial information on similarity index (FSIM) [4] and visual information fidelity (VIF) perceived quality. These features are extracted from numerous [5] use models motivated by HVS and natural scenes statistics, randomly selected patches from images and overall image qual- resulting in better correlations with viewers’ opinion. ity is computed as a weighted sum of patch scores, where weights Numerous machine learning based objective quality metrics are learned during training. The model parameters are initialized have been reported in the literature. -

An Optimization of JPEG-LS Using an Efficient and Low-Complexity
Received April 26th, 2021. Revised June 27th, 2021. Accepted July 23th, 2021. Digital Object Identifier 10.1109/ACCESS.2021.3100747 LOCO-ANS: An Optimization of JPEG-LS Using an Efficient and Low-Complexity Coder Based on ANS TOBÍAS ALONSO , GUSTAVO SUTTER , AND JORGE E. LÓPEZ DE VERGARA High Performance Computing and Networking Research Group, Escuela Politécnica Superior, Universidad Autónoma de Madrid, Spain. {tobias.alonso, gustavo.sutter, jorge.lopez_vergara}@uam.es This work was supported in part by the Spanish Research Agency under the project AgileMon (AEI PID2019-104451RB-C21). ABSTRACT Near-lossless compression is a generalization of lossless compression, where the codec user is able to set the maximum absolute difference (the error tolerance) between the values of an original pixel and the decoded one. This enables higher compression ratios, while still allowing the control of the bounds of the quantization errors in the space domain. This feature makes them attractive for applications where a high degree of certainty is required. The JPEG-LS lossless and near-lossless image compression standard combines a good compression ratio with a low computational complexity, which makes it very suitable for scenarios with strong restrictions, common in embedded systems. However, our analysis shows great coding efficiency improvement potential, especially for lower entropy distributions, more common in near-lossless. In this work, we propose enhancements to the JPEG-LS standard, aimed at improving its coding efficiency at a low computational overhead, particularly for hardware implementations. The main contribution is a low complexity and efficient coder, based on Tabled Asymmetric Numeral Systems (tANS), well suited for a wide range of entropy sources and with simple hardware implementation. -

Benchmarking JPEG XL Image Compression
Benchmarking JPEG XL image compression a a c a b Jyrki Alakuijala , Sami Boukortt , Touradj Ebrahimi , Evgenii Kliuchnikov , Jon Sneyers , Evgeniy Upenikc, Lode Vandevennea, Luca Versaria, Jan Wassenberg1*a a b Google Switzerland, 8002 Zurich, Switzerland; Cloudinary, Santa Clara, CA 95051, USA; c Multimedia Signal Processing Group, École Polytechnique Fédérale de Lausanne, 1015 Lausanne, Switzerland. ABSTRACT JPEG XL is a practical, royalty-free codec for scalable web distribution and efficient compression of high-quality photographs. It also includes previews, progressiveness, animation, transparency, high dynamic range, wide color gamut, and high bit depth. Users expect faithful reproductions of ever higher-resolution images. Experiments performed during standardization have shown the feasibility of economical storage without perceptible quality loss, lossless transcoding of existing JPEG, and fast software encoders and decoders. We analyse the results of subjective and objective evaluations versus existing codecs including HEVC and JPEG. New image codecs have to co-exist with their previous generations for several years. JPEG XL is unique in providing value for both existing JPEGs as well as new users. It includes coding tools to reduce the transmission and storage costs of JPEG by 22% while allowing byte-for-byte exact reconstruction of the original JPEG. Avoiding transcoding and additional artifacts helps to preserve our digital heritage. Applications require fast and low-power decoding. JPEG XL was designed to benefit from multicore and SIMD, and actually decodes faster than JPEG. We report the resulting speeds on ARM and x86 CPUs. To enable reproduction of these results, we open sourced the JPEG XL software in 2019. Keywords: image compression, JPEG XL, perceptual visual quality, image fidelity 1. -

Denoising-Based Image Compression for Connectomics
bioRxiv preprint doi: https://doi.org/10.1101/2021.05.29.445828; this version posted May 30, 2021. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-NC-ND 4.0 International license. Denoising-based Image Compression for Connectomics David Minnen1,#, Michał Januszewski1,#, Alexander Shapson-Coe2, Richard L. Schalek2, Johannes Ballé1, Jeff W. Lichtman2, Viren Jain1 1 Google Research 2 Department of Molecular and Cellular Biology & Center for Brain Science, Harvard University # Equal contribution Abstract Connectomic reconstruction of neural circuits relies on nanometer resolution microscopy which produces on the order of a petabyte of imagery for each cubic millimeter of brain tissue. The cost of storing such data is a significant barrier to broadening the use of connectomic approaches and scaling to even larger volumes. We present an image compression approach that uses machine learning-based denoising and standard image codecs to compress raw electron microscopy imagery of neuropil up to 17-fold with negligible loss of reconstruction accuracy. Main Text Progress in the reconstruction and analysis of neural circuits has recently been accelerated by advances in 3d volume electron microscopy (EM) and automated methods for neuron segmentation and annotation1,2. In particular, contemporary serial section EM approaches are capable of imaging hundreds of megapixels per second3,4, which has led to the successful acquisition of petabyte-scale volumes of human5 and mouse6 cortex. However, scaling further poses substantial challenges to computational infrastructure; nanometer resolution imaging of a whole mouse brain7 could, for example, produce one million terabytes (an exabyte) of data. -

Comprehensive Assessment of Image Compression Algorithms
Comprehensive Assessment of Image Compression Algorithms Michela Testolina, Evgeniy Upenik, and Touradj Ebrahimi Multimedia Signal Processing Group (MMSPG) Ecole Polytechnique F´ed´eralede Lausanne (EPFL) CH-1015 Lausanne, Switzerland Email: firstname.lastname@epfl.ch ABSTRACT JPEG image coding standard has been a dominant format in a wide range of applications in soon three decades since it has been released as an international standard. The landscape of applications and services based on pictures has evolved since the original JPEG image coding algorithm was designed. As a result of progress in the state of the art image coding, several alternative image coding approaches have been proposed to replace the legacy JPEG with mixed results. The majority among them have not been able to displace the unique position that the legacy JPEG currently occupies as the ubiquitous image coding format of choice. Those that have been successful, have been so in specific niche applications. In this paper, we analyze why all attempts to replace JPEG have been limited so far, and discuss additional features other than compression efficiency that need to be present in any modern image coding algorithm to increase its chances of success. Doing so, we compare rate distortion performance of state of the art conventional and learning based image coding, in addition to other desired features in advanced multimedia applications such as transcoding. We conclude the paper by highlighting the remaining challenges that need to be overcome in order to design a successful future generation image coding algorithm. Keywords: Image compression, lossy compression, deep learning, perceptual visual quality, JPEG standard 1. -

Ukládání a Komprese Obrazu
Úvod Reprezentace barvy Kódování a komprese dat Formáty pro ukládání obrazu Komprese videa Literatura Ukládání a komprese obrazu Pavel Strachota FJFI CVUTˇ v Praze 5. dubna 2021 Úvod Reprezentace barvy Kódování a komprese dat Formáty pro ukládání obrazu Komprese videa Literatura Obsah 1 Úvod 2 Reprezentace barvy 3 Kódování a komprese dat 4 Formáty pro ukládání obrazu 5 Komprese videa Úvod Reprezentace barvy Kódování a komprese dat Formáty pro ukládání obrazu Komprese videa Literatura Obsah 1 Úvod 2 Reprezentace barvy 3 Kódování a komprese dat 4 Formáty pro ukládání obrazu 5 Komprese videa Úvod Reprezentace barvy Kódování a komprese dat Formáty pro ukládání obrazu Komprese videa Literatura Reprezentace obrazu vektorová - popis geometrických objekt˚ua jejich vlastností (polohy, barvy, prekrýváníˇ atd.) nezávisí na rozlišení zobrazovacího zarízeníˇ lze libovnolneˇ škálovat priˇ zachování kvality rastrová - popis obrazu pomocí matice pixel˚u konecnéˇ rozlišení vysoká pamet’ovᡠnárocnostˇ =) snaha o kompresi informace Úvod Reprezentace barvy Kódování a komprese dat Formáty pro ukládání obrazu Komprese videa Literatura Obsah 1 Úvod 2 Reprezentace barvy 3 Kódování a komprese dat 4 Formáty pro ukládání obrazu 5 Komprese videa Úvod Reprezentace barvy Kódování a komprese dat Formáty pro ukládání obrazu Komprese videa Literatura Reprezentace barvy cernobílýˇ obraz - 1 bit na pixel šedotónový obraz - 8 bit˚una pixel, 256 stupn˚ušediˇ RGB reprezentace 5+6+5 bit˚u(565 High Color mode) 8+8+8 bit˚uTrue Color mode reprezentace v jiném barevném prostoru -

Coding of Still Pictures
ISO/IEC JTC 1/SC29/WG1N77011 77th Meeting, Macau, China, October 23-27, 2017 ISO/IEC JTC 1/SC 29/WG 1 (ITU-T SG16) Coding of Still Pictures JBIG JPEG Joint Bi-level Image Joint Photographic Experts Group Experts Group TITLE: Draft Call for Proposals for a Next-Generation Image Coding Standard (JPEG XL) SOURCE: WG1 PROJECT: TBD STATUS: Draft REQUESTED ACTION: Provide feedback and response DISTRIBUTION: Public Contact: ISO/IEC JTC 1/SC 29/WG 1 Convener – Prof. Touradj Ebrahimi EPFL/STI/IEL/GR-EB, Station 11, CH-1015 Lausanne, Switzerland Tel: +41 21 693 2606, Fax: +41 21 693 7600, E-mail: [email protected] - 1 - ISO/IEC JTC 1/SC29/WG1N77011 77th Meeting, Macau, China, October 23-27, 2017 Draft Call for Proposals on Next-Generation Image Coding (JPEG XL) Summary The JPEG Committee has launched the Next-Generation Image Coding activity, also referred to as JPEG XL. This activity aims to develop a standard for image coding that offers substantially better compression efficiency than existing image formats (e.g. >60% over JPEG-1), along with features desirable for web distribution and efficient compression of high-quality images. The JPEG Committee intends to publish a final Call for Proposals (CfP) following its 78th meeting (January 2018), with the objective of seeking technologies that fulfil the objectives and scope of the Next- Generation Image Coding activity. This document is a draft of the CfP, and is offered for a public review period ending 19 January 2018. Comments are welcome and should be submitted to the contacts listed in Section 10. -

A Standard Framework For
Vrije Universiteit Brussel JPEG Pleno: a standard framework for representing and signaling plenoptic modalities Schelkens, Peter; Alpaslan, Zahir Y.; Ebrahimi, Touradj; Oh, Kwan-Jung; Pereira, Fernando ; Pinheiro, Antonio; Tabus, Ioan; Chen, Zhibo Published in: Proceedings of SPIE Optics + Photonics: Applications of Digital Image Processing XLI DOI: 10.1117/12.2323404 Publication date: 2018 License: CC BY Document Version: Final published version Link to publication Citation for published version (APA): Schelkens, P., Alpaslan, Z. Y., Ebrahimi, T., Oh, K-J., Pereira, F., Pinheiro, A., ... Chen, Z. (2018). JPEG Pleno: a standard framework for representing and signaling plenoptic modalities. In A. G. Tescher (Ed.), Proceedings of SPIE Optics + Photonics: Applications of Digital Image Processing XLI (Vol. 10752, pp. 107521P). [107521P] (APPLICATIONS OF DIGITAL IMAGE PROCESSING XLI). SPIE. https://doi.org/10.1117/12.2323404 General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain • You may freely distribute the URL identifying the publication in the public portal Take down policy If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. -

Standards Action
PUBLISHED WEEKLY BY THE AMERICAN NATIONAL STANDARDS INSTITUTE 25 WEST 43RD STREET NY, NY 10036 VOL. 52| NO. 33 August 13, 2021 CONTENTS American National Standards Project Initiation Notification System (PINS) ............................................................... 2 Call for Comment on Standards Proposals .................................................................. 5 Final Actions - (Approved ANS) .................................................................................. 17 Call for Members (ANS Consensus Bodies) ................................................................ 25 Accreditation Announcements (Standards Developers) ............................................ 27 Meeting Notices (Standards Developers) .................................................................. 28 American National Standards (ANS) Process ............................................................. 29 ANS Under Continuous Maintenance ........................................................................ 30 ANSI-Accredited Standards Developer Contact Information ..................................... 31 International Standards ISO and IEC Draft Standards ....................................................................................... 34 ISO Newly Published Standards ................................................................................. 39 International Organization for Standardization (ISO) ................................................ 41 Registration of Organization Names in the United States ......................................... -

Evaluating Image Compression Methods on Two Dimensional Height Representations
Linköping University | Department of Electrical Engineering Master’s thesis, 30 ECTS | Information Coding 2020 | LIU-ISY/ISY-A-EX-A--20/5344--SE Evaluating Image Compression Methods on Two Dimensional Height Representations Oscar Sjöberg Supervisor : Harald Nautsch Examiner : Ingemar Ragnemalm External supervisor : Filip Thorardsson Linköpings universitet SE–581 83 Linköping +46 13 28 10 00 , www.liu.se Upphovsrätt Detta dokument hålls tillgängligt på Internet - eller dess framtida ersättare - under 25 år från publicer- ingsdatum under förutsättning att inga extraordinära omständigheter uppstår. Tillgång till dokumentet innebär tillstånd för var och en att läsa, ladda ner, skriva ut enstaka ko- pior för enskilt bruk och att använda det oförändrat för ickekommersiell forskning och för undervis- ning. Överföring av upphovsrätten vid en senare tidpunkt kan inte upphäva detta tillstånd. All annan användning av dokumentet kräver upphovsmannens medgivande. För att garantera äktheten, säker- heten och tillgängligheten finns lösningar av teknisk och administrativ art. Upphovsmannens ideella rätt innefattar rätt att bli nämnd som upphovsman i den omfattning som god sed kräver vid användning av dokumentet på ovan beskrivna sätt samt skydd mot att dokumentet ändras eller presenteras i sådan form eller i sådant sammanhang som är kränkande för upphovsman- nens litterära eller konstnärliga anseende eller egenart. För ytterligare information om Linköping University Electronic Press se förlagets hemsida http://www.ep.liu.se/. Copyright The publishers will keep this document online on the Internet - or its possible replacement - for a period of 25 years starting from the date of publication barring exceptional circumstances. The online availability of the document implies permanent permission for anyone to read, to down- load, or to print out single copies for his/hers own use and to use it unchanged for non-commercial research and educational purpose. -

Coding of Still Pictures
ISO/IEC JTC 1/SC29/WG1 N83058 83rd JPEG Meeting, Geneva, Switzerland, 17-22 March 2019 ISO/IEC JTC 1/SC 29/WG 1 (ITU-T SG16) Coding of Still Pictures JBIG JPEG Joint Bi-level Image Joint Photographic Experts Group Experts Group TITLE: Report on the State-of-the-art of Learning based Image Coding SOURCE: Requirements EDITORS: João Ascenso, Pinar Akayzi STATUS: Final REQUESTED ACTION: Distribute DISTRIBUTION: Public Contact: ISO/IEC JTC 1/SC 29/WG 1 Convener – Prof. Touradj Ebrahimi EPFL/STI/IEL/GR-EB, Station 11, CH-1015 Lausanne, Switzerland Tel: +41 21 693 2606, Fax: +41 21 693 7600, E-mail: [email protected] Page 1 1. Purpose of This Document In the last few years, several learning-based image coding solutions have been proposed to take advantage of recent advances in this field. The driving force was the development of improved neural network models for several image processing areas, such as denoising and super-resolution, which have taken advantage of the availability of large image datasets and special hardware, such as the highly parallelizable graphic processing units (GPUs). This document marks the beginning of the work to be conducted in JPEG and has the following objectives: • Present a list of learning-based image coding solutions from the literature in an organized way. • Present a list of software implementations of deep learning-based image codecs public available. • Present a list of data sets that may be used for exploration studies. Despite the advances, there are several challenges in this type of coding solutions, namely which encoder/decoder architectures are more promising (e.g.