Ground Interpolation for the Theory of Equality
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Group Developed Weighing Matrices∗
AUSTRALASIAN JOURNAL OF COMBINATORICS Volume 55 (2013), Pages 205–233 Group developed weighing matrices∗ K. T. Arasu Department of Mathematics & Statistics Wright State University 3640 Colonel Glenn Highway, Dayton, OH 45435 U.S.A. Jeffrey R. Hollon Department of Mathematics Sinclair Community College 444 W 3rd Street, Dayton, OH 45402 U.S.A. Abstract A weighing matrix is a square matrix whose entries are 1, 0 or −1,such that the matrix times its transpose is some integer multiple of the identity matrix. We examine the case where these matrices are said to be devel- oped by an abelian group. Through a combination of extending previous results and by giving explicit constructions we will answer the question of existence for 318 such matrices of order and weight both below 100. At the end, we are left with 98 open cases out of a possible 1,022. Further, some of the new results provide insight into the existence of matrices with larger weights and orders. 1 Introduction 1.1 Group Developed Weighing Matrices A weighing matrix W = W (n, k) is a square matrix, of order n, whose entries are in t the set wi,j ∈{−1, 0, +1}. This matrix satisfies WW = kIn, where t denotes the matrix transpose, k is a positive integer known as the weight, and In is the identity matrix of size n. Definition 1.1. Let G be a group of order n.Ann×n matrix A =(agh) indexed by the elements of the group G (such that g and h belong to G)issaidtobeG-developed if it satisfies the condition agh = ag+k,h+k for all g, h, k ∈ G. -

Wearable-Based Pedestrian Inertial Navigation with Constraints Based on Biomechanical Models
Wearable-based pedestrian inertial navigation with constraints based on biomechanical models Dina Bousdar Ahmed∗ and Kai Metzger† ∗ Institute of Communications and Navigation German Aerospace Center (DLR), Munich, Germany Email: [email protected] † Technical University of Munich, Germany Email: kai [email protected] Abstract—Our aim in this paper is to analyze inertial nav- sensor to correct the heading estimation [4]. The combina- igation systems (INSs) from the biomechanical point of view. tion of inertial sensors and WiFi measurements is useful in We wanted to improve the performance of a thigh INS by indoor environments. Chen et al. use the position estimated applying biomechanical constraints. To that end, we propose a biomechanical model of the leg. The latter establishes a through WiFi measurements to correct the position estimates relationship between the orientation of the thigh INS and the of an inertial navigation system [5]. The latter is based on a kinematic motion of the leg. This relationship allows to observe smartphone. the effect that the orientation errors have in the expected motion The detection of known landmarks, e.g. turns, elevators, etc, of the leg. We observe that the errors in the orientation estimation can improve the position estimation. Chen et al. [5] incorporate of an INS translate into incoherent human motion. Based on this analysis, we proposed a modified thigh INS to integrate landmarks to improve the performance of their navigation biomechanical constraints. The results show that the proposed system. Munoz et al. [6] use also landmarks to correct directly system outperforms the thigh INS in 50% regarding distance the heading estimation of a thigh-mounted inertial navigation error and 32% regarding orientation error. -

Preparation and Investigation of Highly Charged Ions in a Penning Trap for the Determination of Atomic Magnetic Moments
Preparation and Investigation of Highly Charged Ions in a Penning Trap for the Determination of Atomic Magnetic Moments Präparation und Untersuchung von hochgeladenen Ionen in einer Penning-Falle zur Bestimmung atomarer magnetischer Momente Dissertation approved by the Fachbereich Physik of the Technische Universität Darmstadt in fulfillment of the requirements for the degree of Doctor of Natural Sciences (Dr. rer. nat.) by Dipl.-Phys. Marco Wiesel from Neustadt an der Weinstraße June 2017 — Darmstadt — D 17 Preparation and Investigation of Highly Charged Ions in a Penning Trap for the Determination of Atomic Magnetic Moments Dissertation approved by the Fachbereich Physik of the Technische Universität Darmstadt in fulfillment of the requirements for the degree of Doctor of Natural Sciences (Dr. rer. nat.) by Dipl.-Phys. Marco Wiesel from Neustadt an der Weinstraße 1. Referee: Prof. Dr. rer. nat. Gerhard Birkl 2. Referee: Privatdozent Dr. rer. nat. Wolfgang Quint Submission date: 18.04.2017 Examination date: 24.05.2017 Darmstadt 2017 D 17 Title: The logo of ARTEMIS – AsymmetRic Trap for the measurement of Electron Magnetic moments in IonS. Bitte zitieren Sie dieses Dokument als: URN: urn:nbn:de:tuda-tuprints-62803 URL: http://tuprints.ulb.tu-darmstadt.de/id/eprint/6280 Dieses Dokument wird bereitgestellt von tuprints, E-Publishing-Service der TU Darmstadt http://tuprints.ulb.tu-darmstadt.de [email protected] Die Veröffentlichung steht unter folgender Creative Commons Lizenz: Namensnennung – Keine kommerzielle Nutzung – Keine Bearbeitung 4.0 International https://creativecommons.org/licenses/by-nc-nd/4.0/ Abstract The ARTEMIS experiment aims at measuring magnetic moments of electrons bound in highly charged ions that are stored in a Penning trap. -

Operating Manual R&S NRP-Z22
Operating Manual Average Power Sensor R&S NRP-Z22 1137.7506.02 R&S NRP-Z23 1137.8002.02 R&S NRP-Z24 1137.8502.02 Test and Measurement 1137.7870.12-07- 1 Dear Customer, R&S® is a registered trademark of Rohde & Schwarz GmbH & Co. KG Trade names are trademarks of the owners. 1137.7870.12-07- 2 Basic Safety Instructions Always read through and comply with the following safety instructions! All plants and locations of the Rohde & Schwarz group of companies make every effort to keep the safety standards of our products up to date and to offer our customers the highest possible degree of safety. Our products and the auxiliary equipment they require are designed, built and tested in accordance with the safety standards that apply in each case. Compliance with these standards is continuously monitored by our quality assurance system. The product described here has been designed, built and tested in accordance with the EC Certificate of Conformity and has left the manufacturer’s plant in a condition fully complying with safety standards. To maintain this condition and to ensure safe operation, you must observe all instructions and warnings provided in this manual. If you have any questions regarding these safety instructions, the Rohde & Schwarz group of companies will be happy to answer them. Furthermore, it is your responsibility to use the product in an appropriate manner. This product is designed for use solely in industrial and laboratory environments or, if expressly permitted, also in the field and must not be used in any way that may cause personal injury or property damage. -

Z1 Z2 Z4 Z5 Z6 Z7 Z3 Z8
Illinois State Police Division of Criminal Investigation JO DAVIESS STEPHENSON WINNEBAGO B McHENRY LAKE DIVISION OF CRIMINAL INVESTIGATION - O O Colonel Mark R. Peyton Pecatonica 16 N E Chicago Lieutenant Colonel Chris Trame CARROLL OGLE Chief of Staff DE KALB KANE Elgin COOK Lieutenant Jonathan Edwards NORTH 2 Z1DU PAGE C WHITESIDE LEE 15 1 Z2 NORTH COMMAND - Sterling KENDALL WILL Major Michael Witt LA SALLE 5 Zone 1 - (Districts Chicago and 2) East Moline HENRY BUREAU Captain Matthew Gainer 7 17 Joliet ROCK ISLAND GRUNDY Zone 2 - (Districts 1, 7, 16) LaSalle MERCER Captain Christopher Endress KANKAKEE PUTNAM Z3 Zone 3 - (Districts 5, 17, 21) KNOX STARK Captain Richard Wilk H MARSHALL LIVINGSTON E WARREN Statewide Gaming Command IROQUOIS N PEORIA 6 Captain Sean Brannon D WOODFORD E Pontiac Ashkum CENTRAL R 8 Metamora S 21 O McLEAN N FULTON CENTRAL COMMAND - McDONOUGH HANCOCK TAZEWELL Captain Calvin Brown, Interim Macomb FORD VERMILION Zone 4 - (Districts 8, 9, 14, 20) 14 MASON CHAMPAIGN Captain Don Payton LOGAN DE WITT SCHUYLER Zone 5 - (Districts 6, 10) PIATT ADAMS Captain Jason Henderson MENARD Investigative Support Command CASS MACON Pesotum BROWN Captain Aaron Fullington Z4 10 SANGAMON Medicaid Fraud Control Bureau MORGAN DOUGLAS EDGAR PIKE 9 Z5 Captain William Langheim Pittsfield SCOTT MOULTRIE Springfield 20 CHRISTIAN COLES SHELBY GREENE MACOUPIN SOUTH COMMAND - CLARK Major William Sons C CUMBERLAND A MONTGOMERY L Zone 6 - (Districts 11, 18) H Litchfield 18 O Lieutenant Abigail Keller, Interim JERSEY FAYETTE EFFINGHAM JASPER U Zone 7 - (Districts 13, 22) N Effingham 12 CRAWFORD Z6 BOND Captain Nicholas Dill MADISON Zone 8 - (Districts 12, 19) CLAY Collinsville RICHLAND LAWRENCE Captain Ryan Shoemaker MARION 11 Special Operations Command ST. -

Konrad Zuse Und Die Schweiz
Research Collection Report Konrad Zuse und die Schweiz Relaisrechner Z4 an der ETH Zürich : Rechenlocher M9 für die Schweizer Remington Rand : Eigenbau des Röhrenrechners ERMETH : Zeitzeugenbericht zur Z4 : unbekannte Dokumente zur M9 : ein Beitrag zu den Anfängen der Schweizer Informatikgeschichte Author(s): Bruderer, Herbert Publication Date: 2011 Permanent Link: https://doi.org/10.3929/ethz-a-006517565 Rights / License: In Copyright - Non-Commercial Use Permitted This page was generated automatically upon download from the ETH Zurich Research Collection. For more information please consult the Terms of use. ETH Library Konrad Zuse und die Schweiz Relaisrechner Z4 an der ETH Zürich Rechenlocher M9 für die Schweizer Remington Rand Eigenbau des Röhrenrechners ERMETH Zeitzeugenbericht zur Z4 Unbekannte Dokumente zur M9 Ein Beitrag zu den Anfängen der Schweizer Informatikgeschichte Herbert Bruderer ETH Zürich Departement Informatik Professur für Informationstechnologie und Ausbildung Zürich, Juli 2011 Adresse des Verfassers: Herbert Bruderer ETH Zürich Informationstechnologie und Ausbildung CAB F 14 Universitätsstrasse 6 CH-8092 Zürich Telefon: +41 44 632 73 83 Telefax: +41 44 632 13 90 [email protected] www.ite.ethz.ch privat: Herbert Bruderer Bruderer Informatik Seehaldenstrasse 26 Postfach 47 CH-9401 Rorschach Telefon: +41 71 855 77 11 Telefax: +41 71 855 72 11 [email protected] Titelbild: Relaisschränke der Z4 (links: Heinz Rutishauser, rechts: Ambros Speiser), ETH Zürich 1950, © ETH-Bibliothek Zürich, Bildarchiv Bild 4. Umschlagseite: Verabschiedungsrede von Konrad Zuse an der Z4 am 6. Juli 1950 in der Zuse KG in Neukirchen (Kreis Hünfeld) © Privatarchiv Horst Zuse, Berlin Eidgenössische Technische Hochschule Zürich Departement Informatik Professur für Informationstechnologie und Ausbildung CH-8092 Zürich www.abz.inf.ethz.ch 1. -

P the Pioneers and Their Computers
The Videotape Sources: The Pioneers and their Computers • Lectures at The Compp,uter Museum, Marlboro, MA, September 1979-1983 • Goal: Capture data at the source • The first 4: Atanasoff (ABC), Zuse, Hopper (IBM/Harvard), Grosch (IBM), Stibitz (BTL) • Flowers (Colossus) • ENIAC: Eckert, Mauchley, Burks • Wilkes (EDSAC … LEO), Edwards (Manchester), Wilkinson (NPL ACE), Huskey (SWAC), Rajchman (IAS), Forrester (MIT) What did it feel like then? • What were th e comput ers? • Why did their inventors build them? • What materials (technology) did they build from? • What were their speed and memory size specs? • How did they work? • How were they used or programmed? • What were they used for? • What did each contribute to future computing? • What were the by-products? and alumni/ae? The “classic” five boxes of a stored ppgrogram dig ital comp uter Memory M Central Input Output Control I O CC Central Arithmetic CA How was programming done before programming languages and O/Ss? • ENIAC was programmed by routing control pulse cables f ormi ng th e “ program count er” • Clippinger and von Neumann made “function codes” for the tables of ENIAC • Kilburn at Manchester ran the first 17 word program • Wilkes, Wheeler, and Gill wrote the first book on programmiidbBbbIiSiing, reprinted by Babbage Institute Series • Parallel versus Serial • Pre-programming languages and operating systems • Big idea: compatibility for program investment – EDSAC was transferred to Leo – The IAS Computers built at Universities Time Line of First Computers Year 1935 1940 1945 1950 1955 ••••• BTL ---------o o o o Zuse ----------------o Atanasoff ------------------o IBM ASCC,SSEC ------------o-----------o >CPC ENIAC ?--------------o EDVAC s------------------o UNIVAC I IAS --?s------------o Colossus -------?---?----o Manchester ?--------o ?>Ferranti EDSAC ?-----------o ?>Leo ACE ?--------------o ?>DEUCE Whirl wi nd SEAC & SWAC ENIAC Project Time Line & Descendants IBM 701, Philco S2000, ERA.. -

Nonlinear Control of Underactuated Mechanical Systems with Application to Robotics and Aerospace Vehicles
Nonlinear Control of Underactuated Mechanical Systems with Application to Robotics and Aerospace Vehicles by Reza Olfati-Saber Submitted to the Department of Electrical Engineering and Computer Science in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Electrical Engineering and Computer Science at the MASSACHUSETTS INSTITUTE OF TECHNOLOGY February 2001 © Massachusetts Institute of Technology 2001. All rights reserved. Author ................................................... Department of Electrical Engineering and Computer Science January 15, 2000 C ertified by.......................................................... Alexandre Megretski, Associate Professor of Electrical Engineering Thesis Supervisor Accepted by............................................ Arthur C. Smith Chairman, Department Committee on Graduate Students Nonlinear Control of Underactuated Mechanical Systems with Application to Robotics and Aerospace Vehicles by Reza Olfati-Saber Submitted to the Department of Electrical Engineering and Computer Science on January 15, 2000, in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Electrical Engineering and Computer Science Abstract This thesis is devoted to nonlinear control, reduction, and classification of underac- tuated mechanical systems. Underactuated systems are mechanical control systems with fewer controls than the number of configuration variables. Control of underactu- ated systems is currently an active field of research due to their broad applications in Robotics, Aerospace Vehicles, and Marine Vehicles. The examples of underactuated systems include flexible-link robots, nobile robots, walking robots, robots on mo- bile platforms, cars, locomotive systems, snake-type and swimming robots, acrobatic robots, aircraft, spacecraft, helicopters, satellites, surface vessels, and underwater ve- hicles. Based on recent surveys, control of general underactuated systems is a major open problem. Almost all real-life mechanical systems possess kinetic symmetry properties, i.e. -

Bridge Measurement Analysis
Bridge Measurement Analysis Svetlana Avramov-Zamurovic1, Bryan Waltrip2 and Andrew Koffman2 1United States Naval Academy, Weapons and Systems Engineering Department Annapolis, MD 21402, Telephone: 410 293 6124 Email: [email protected] 2National Institute of Standards and Technology†, Electricity Division Gaithersburg, MD 21899. Telephone: 301 975 2438, Email: [email protected] Introduction At the United States Academy there are several engineering majors, including Systems Engineering. This program offers excellent systems integration education. In particular the major concentrates on control of electrical, computer and mechanical systems. In addition to several tracks, students have the opportunity to independently research a field of interest. This is a great opportunity for teachers and students to pursue more in-depth analyses. This paper will describe one such experiment in the field of metrology. Very often engineering laboratories at undergraduate schools are well equipped with power supplies, signal generators, oscilloscopes and general-purpose multimeters. This set allows teachers and students to set up test-beds for most of the basic electronics circuits studied in different engineering tracks. Modern instrumentation is in general user-friendly and students like using the equipment. However, students are often not aware that there are two pieces of information necessary to establish a measurement result: the numerical value of the measured quantity and the uncertainty with which that measurement was performed. In order to achieve high measurement accuracy, more complex measurement systems must be developed. This paper will describe the process of analyzing a bridge measurement using MATLAB‡. Measurement Bridge One of the basic circuits that demonstrate the concept of a current/voltage divider is a Wheatstone bridge (given in Figure 1.) A source voltage is applied to a parallel connection of impedances. -

Konrad Zuse the Computer- My Life
Konrad Zuse The Computer- My Life Konrad Zuse The Computer- My Life With Forewords byEL.Bauer and H. Zemanek Springer-Verlag Berlin Heidelberg GmbH Professor Dr. Ing. E. h. Dr. mult. rer. nat. h.c. Konrad Zuse 1m Haselgrund 21, D-36088 Hunfeld, Germany Editor: Dr. Hans Wossner, Springer-Verlag Heidelberg Translators: Patricia McKenna, New York J.Andrew Ross, Springer-Verlag Heidelberg Titl e of the original German edition: Der Computer - Mein Lebenswerk, 1993 © Springer-Verlag Berlin Heidelberg 1984, 1986, 1990, 1993 Computing Reviews Classification (1991) : K. 2, A. 0 With 68 Figures ISBN 978-3-642-08 151 -4 ISBN 978-3-662-02931-2 (eBook) DOI 10.1007/978-3-662-02931-2 Libary of Congress Cataloging-in-Publication Data . Zuse, Konr ad . (Computer. mein Lebensw erk . English) Th e computer, my life / Konrad Zuse;with for eword s bv F.L. Bauer and H. Zemanek. p. cm. Includes bibliographical references and index. I. Zuse, Konrad. 2. Computers -Germany - History . 3. Computer engineers - Germany - Biography. I. Titl e. TK7885.22.Z87A3 1993 62I.39'092-dc20 [B] 93-18574 This work is subject to copyright. All rights are reserved , whether the whole world or part for the mat erial is concerned , specifically the rights of translation, reprinting, reuse ofillustrati- ons, recitation, broadcasting , reproduction on microfilm or in any ot her way, and storage in data banks. Dupli cation of this publication or parts thereof is permitted only under the pro- visions of German Copyr ight Law of September 9, 1965, in its current version , and permissi- on for use must always be obtained from Springer-Verlag. -

The Z1: Architecture and Algorithms of Konrad Zuse's First Computer
The Z1: Architecture and Algorithms of Konrad Zuse’s First Computer Raul Rojas Freie Universität Berlin June 2014 Abstract This paper provides the first comprehensive description of the Z1, the mechanical computer built by the German inventor Konrad Zuse in Berlin from 1936 to 1938. The paper describes the main structural elements of the machine, the high-level architecture, and the dataflow between components. The computer could perform the four basic arithmetic operations using floating-point numbers. Instructions were read from punched tape. A program consisted of a sequence of arithmetical operations, intermixed with memory store and load instructions, interrupted possibly by input and output operations. Numbers were stored in a mechanical memory. The machine did not include conditional branching in the instruction set. While the architecture of the Z1 is similar to the relay computer Zuse finished in 1941 (the Z3) there are some significant differences. The Z1 implements operations as sequences of microinstructions, as in the Z3, but does not use rotary switches as micro- steppers. The Z1 uses a digital incrementer and a set of conditions which are translated into microinstructions for the exponent and mantissa units, as well as for the memory blocks. Microinstructions select one out of 12 layers in a machine with a 3D mechanical structure of binary mechanical elements. The exception circuits for mantissa zero, necessary for normalized floating-point, were lacking; they were first implemented in the Z3. The information for this article was extracted from careful study of the blueprints drawn by Zuse for the reconstruction of the Z1 for the German Technology Museum in Berlin, from some letters, and from sketches in notebooks. -
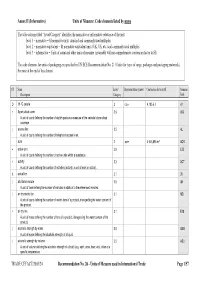
Units of Measure Used in International Trade Page 1/57 Annex II (Informative) Units of Measure: Code Elements Listed by Name
Annex II (Informative) Units of Measure: Code elements listed by name The table column titled “Level/Category” identifies the normative or informative relevance of the unit: level 1 – normative = SI normative units, standard and commonly used multiples level 2 – normative equivalent = SI normative equivalent units (UK, US, etc.) and commonly used multiples level 3 – informative = Units of count and other units of measure (invariably with no comprehensive conversion factor to SI) The code elements for units of packaging are specified in UN/ECE Recommendation No. 21 (Codes for types of cargo, packages and packaging materials). See note at the end of this Annex). ST Name Level/ Representation symbol Conversion factor to SI Common Description Category Code D 15 °C calorie 2 cal₁₅ 4,185 5 J A1 + 8-part cloud cover 3.9 A59 A unit of count defining the number of eighth-parts as a measure of the celestial dome cloud coverage. | access line 3.5 AL A unit of count defining the number of telephone access lines. acre 2 acre 4 046,856 m² ACR + active unit 3.9 E25 A unit of count defining the number of active units within a substance. + activity 3.2 ACT A unit of count defining the number of activities (activity: a unit of work or action). X actual ton 3.1 26 | additional minute 3.5 AH A unit of time defining the number of minutes in addition to the referenced minutes. | air dry metric ton 3.1 MD A unit of count defining the number of metric tons of a product, disregarding the water content of the product.