DOCSLIB.ORG

Nuclear Equations

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Nuclear Equations Nuclear Equations In nuclear equations, we balance nucleons (protons and neutrons). The atomic number (number of protons) and the mass number (number of nucleons) are conserved during the reaction. Nuclear Equations Alpha Decay Nuclear Equations Beta Decay Nuclear Equations Beta Decay Nuclear Equations Positron Emission: A positron is a particle equal in mass to an electron but with opposite charge. Nuclear Equations Electron Capture: A nucleus absorbs an electron from the inner shell. Nuclear Equations EXAMPLE 4.1 Balancing Nuclear Equations Write balanced nuclear equations for each of the following processes. In each case, indicate what new element is formed. a. Plutonium-239 emits an alpha particle when it decays. b. Protactinium-234 undergoes beta decay. c. Carbon-11 emits a positron when it decays. d. Carbon-11 undergoes electron capture. EXAMPLE 4.1 Balancing Nuclear Equations continued Exercise 4.1 Write balanced nuclear equations for each of the following processes. In each case, indicate what new element is formed. a. Radium-226 decays by alpha emission. b. Sodium-24 undergoes beta decay. c. Gold-188 decays by positron emission. d. Argon-37 undergoes electron capture. EXAMPLE 4.2 More Nuclear Equations 5 In the upper atmosphere, a nitrogen-14 nucleus absorbs a neutron. A carbon-14 nucleus and another particle are formed. What is the other particle? Half-Life Half-life of a radioactive sample is the time required for ½ of the material to undergo radioactive decay. Half-Life Half-Life Fraction Remaining = 1/2n Half-life T1/2 = 0.693/ k(decay constant) If you know how much you started with and how much you ended with, then you can determine the number of half-lives. If you also know the start and end time, you can divide the time by the number of half- lives to give you the T1/2. Half-life To determine starting amounts or ending amounts: ln(Nt/No) = -kt Nt is the number of radioactive nuclei at your ending No is the number of radioactive nuclei at the start K is the decay constant Radioisotopic Dating Radioisotopic Dating Carbon-14 Dating: The half-life of carbon-14 is 5730 years. Carbon-14 is formed in the upper atmosphere by the bombardment of ordinary nitrogen atoms by neutrons from cosmic rays. Radioisotopic Dating Tritium Dating: Tritium is a radioactive isotope of hydrogen. It has a half-life of 12.26 years and can be used for dating objects up to 100 years old. Nuclear Chain Reaction Fission of one nucleus produces neutrons that can cause the fission of other nuclei, thus setting off a chain reaction. Manhattan Project The Manhattan Project was launched by President Roosevelt in 1939. It consisted of 4 separate research teams attempting to: a. Sustain the nuclear fission reaction. b. Enrich uranium. c. Make fissionable plutonium-239. d. Construct a fission atomic bomb. Manhattan Project Replicas of “Little Boy” (dropped on Hiroshima) and “Fat Man” (dropped on Nagasaki). Manhattan Project Mushroom cloud over Nagasaki from the detonation of “Fat Man,” August 9, 1945. Radioactive Fallout Many radioactive isotopes are produced in a nuclear bomb blast. Some are particularly harmful to humans. Among these are strontium-90 and iodine-131. Strontium-90: Half-life = 28.5 years, chemically similar to calcium. Obtained from dairy and vegetable products and accumulates in bone. Iodine-131: Half-life = 8 days. Concentrates in the thyroid glands. Nuclear Power Plants Civilian nuclear power plants use less enriched uranium (2.5-3.5% uranium-235 rather than 90% for weapons-grade). The nuclear chain reaction is controlled for the slow release of heat energy. The heat is used to make steam, which turns a turbine to produce electricity. The Nuclear Age .
Load more

Recommended publications
  • Chapter 3 the Fundamentals of Nuclear Physics Outline Natural
    Outline Chapter 3 The Fundamentals of Nuclear • Terms: activity, half life, average life • Nuclear disintegration schemes Physics • Parent-daughter relationships Radiation Dosimetry I • Activation of isotopes Text: H.E Johns and J.R. Cunningham, The physics of radiology, 4th ed. http://www.utoledo.edu/med/depts/radther Natural radioactivity Activity • Activity – number of disintegrations per unit time; • Particles inside a nucleus are in constant motion; directly proportional to the number of atoms can escape if acquire enough energy present • Most lighter atoms with Z<82 (lead) have at least N Average one stable isotope t / ta A N N0e lifetime • All atoms with Z > 82 are radioactive and t disintegrate until a stable isotope is formed ta= 1.44 th • Artificial radioactivity: nucleus can be made A N e0.693t / th A 2t / th unstable upon bombardment with neutrons, high 0 0 Half-life energy protons, etc. • Units: Bq = 1/s, Ci=3.7x 1010 Bq Activity Activity Emitted radiation 1 Example 1 Example 1A • A prostate implant has a half-life of 17 days. • A prostate implant has a half-life of 17 days. If the What percent of the dose is delivered in the first initial dose rate is 10cGy/h, what is the total dose day? N N delivered? t /th t 2 or e Dtotal D0tavg N0 N0 A. 0.5 A. 9 0.693t 0.693t B. 2 t /th 1/17 t 2 2 0.96 B. 29 D D e th dt D h e th C. 4 total 0 0 0.693 0.693t /th 0.6931/17 C.
    [Show full text]
  • Electron Capture in Stars
    Electron capture in stars K Langanke1;2, G Mart´ınez-Pinedo1;2;3 and R.G.T. Zegers4;5;6 1GSI Helmholtzzentrum f¨urSchwerionenforschung, D-64291 Darmstadt, Germany 2Institut f¨urKernphysik (Theoriezentrum), Department of Physics, Technische Universit¨atDarmstadt, D-64298 Darmstadt, Germany 3Helmholtz Forschungsakademie Hessen f¨urFAIR, GSI Helmholtzzentrum f¨ur Schwerionenforschung, D-64291 Darmstadt, Germany 4 National Superconducting Cyclotron Laboratory, Michigan State University, East Lansing, Michigan 48824, USA 5 Joint Institute for Nuclear Astrophysics: Center for the Evolution of the Elements, Michigan State University, East Lansing, Michigan 48824, USA 6 Department of Physics and Astronomy, Michigan State University, East Lansing, Michigan 48824, USA E-mail: [email protected], [email protected], [email protected] Abstract. Electron captures on nuclei play an essential role for the dynamics of several astrophysical objects, including core-collapse and thermonuclear supernovae, the crust of accreting neutron stars in binary systems and the final core evolution of intermediate mass stars. In these astrophysical objects, the capture occurs at finite temperatures and at densities at which the electrons form a degenerate relativistic electron gas. The capture rates can be derived in perturbation theory where allowed nuclear transitions (Gamow-Teller transitions) dominate, except at the higher temperatures achieved in core-collapse supernovae where also forbidden transitions contribute significantly to the rates. There has been decisive progress in recent years in measuring Gamow-Teller (GT) strength distributions using novel experimental techniques based on charge-exchange reactions. These measurements provide not only data for the GT distributions of ground states for many relevant nuclei, but also serve as valuable constraints for nuclear models which are needed to derive the capture rates for the arXiv:2009.01750v1 [nucl-th] 3 Sep 2020 many nuclei, for which no data exist yet.
    [Show full text]
  • 2.3 Neutrino-Less Double Electron Capture - Potential Tool to Determine the Majorana Neutrino Mass by Z.Sujkowski, S Wycech
    DEPARTMENT OF NUCLEAR SPECTROSCOPY AND TECHNIQUE 39 The above conservatively large systematic hypothesis. TIle quoted uncertainties will be soon uncertainty reflects the fact that we did not finish reduced as our analysis progresses. evaluating the corrections fully in the current analysis We are simultaneously recording a large set of at the time of this writing, a situation that will soon radiative decay events for the processes t e'v y change. This result is to be compared with 1he and pi-+eN v y. The former will be used to extract previous most accurate measurement of McFarlane the ratio FA/Fv of the axial and vector form factors, a et al. (Phys. Rev. D 1984): quantity of great and longstanding interest to low BR = (1.026 ± 0.039)'1 I 0 energy effective QCD theory. Both processes are as well as with the Standard Model (SM) furthermore very sensitive to non- (V-A) admixtures in prediction (Particle Data Group - PDG 2000): the electroweak lagLangian, and thus can reveal BR = (I 038 - 1.041 )*1 0-s (90%C.L.) information on physics beyond the SM. We are currently analyzing these data and expect results soon. (1.005 - 1.008)* 1W') - excl. rad. corr. Tale 1 We see that even working result strongly confirms Current P1IBETA event sxpelilnentstatistics, compared with the the validity of the radiative corrections. Another world data set. interesting comparison is with the prediction based on Decay PIBETA World data set the most accurate evaluation of the CKM matrix n >60k 1.77k element V d based on the CVC hypothesis and ihce >60 1.77_ _ _ results
    [Show full text]
  • Theory of Nuclear Excitation by Electron Capture for Heavy Ions
    Theory of nuclear excitation by electron capture for heavy ions Inaugural Dissertation zur Erlangung des Doktorgrades der Naturwissenschaften der Justus-Liebig-Universit¨at Gießen Fachbereich 07 vorgelegt von Adriana Gagyi-P´alffy aus Bukarest, Rum¨anien Gießen 2006 Dekan: Prof. Dr. Volker Metag 1. Berichterstatter: Prof. Dr. Werner Scheid 2. Berichterstatter: Prof. Dr. Alfred Muller¨ Tag der mundlic¨ hen Prufung:¨ Contents Introduction 5 Aim and motivation of this thesis . 6 Contents of this thesis . 7 1 Theory of electron recombination 9 1.1 Decomposition of the Fock space . 11 1.2 The total Hamiltonian of the system . 12 1.3 Expansion of the transition operator . 14 1.4 Total cross section for NEEC . 18 2 Theory of NEEC 21 2.1 Nuclear model . 21 2.2 NEEC rates for electric transitions . 27 2.3 NEEC rates for magnetic transitions . 29 3 Total cross sections for NEEC 31 3.1 Numerical results . 31 3.2 Possible experimental observation of NEEC . 37 3.2.1 Electron Beam Ion Traps . 37 3.2.2 Ion Accelerators . 40 4 Interference between NEEC and RR 45 4.1 Interference term in the total cross section . 45 4.2 Electric transitions . 50 4.3 Magnetic transitions . 52 4.4 Numerical results . 54 5 Angular distribution of emitted radiation 59 5.1 Alignment of the excited nuclear state . 60 5.2 Radiative decay of the excited nuclear state . 62 5.3 Numerical results . 65 Summary and Outlook 73 Summary . 73 Outlook . 74 Deutschsprachige Zusammenfassung 77 3 CONTENTS Appendix A The magnetic Hamiltonian 81 B Magnetic transitions in the nuclear collective model 85 C Calculation of matrix elements involving spherical tensors 89 Bibliography 95 Acknowledgments 107 4 Introduction When Niels Bohr proposed in 1913 his first model of the atom, he depicted it as having a small and dense positively charged nucleus, surrounded by the orbiting electrons.
    [Show full text]
  • Introduction to Nuclear Physics and Nuclear Decay
    NM Basic Sci.Intro.Nucl.Phys. 06/09/2011 Introduction to Nuclear Physics and Nuclear Decay Larry MacDonald [email protected] Nuclear Medicine Basic Science Lectures September 6, 2011 Atoms Nucleus: ~10-14 m diameter ~1017 kg/m3 Electron clouds: ~10-10 m diameter (= size of atom) water molecule: ~10-10 m diameter ~103 kg/m3 Nucleons (protons and neutrons) are ~10,000 times smaller than the atom, and ~1800 times more massive than electrons. (electron size < 10-22 m (only an upper limit can be estimated)) Nuclear and atomic units of length 10-15 = femtometer (fm) 10-10 = angstrom (Å) Molecules mostly empty space ~ one trillionth of volume occupied by mass Water Hecht, Physics, 1994 (wikipedia) [email protected] 2 [email protected] 1 NM Basic Sci.Intro.Nucl.Phys. 06/09/2011 Mass and Energy Units and Mass-Energy Equivalence Mass atomic mass unit, u (or amu): mass of 12C ≡ 12.0000 u = 19.9265 x 10-27 kg Energy Electron volt, eV ≡ kinetic energy attained by an electron accelerated through 1.0 volt 1 eV ≡ (1.6 x10-19 Coulomb)*(1.0 volt) = 1.6 x10-19 J 2 E = mc c = 3 x 108 m/s speed of light -27 2 mass of proton, mp = 1.6724x10 kg = 1.007276 u = 938.3 MeV/c -27 2 mass of neutron, mn = 1.6747x10 kg = 1.008655 u = 939.6 MeV/c -31 2 mass of electron, me = 9.108x10 kg = 0.000548 u = 0.511 MeV/c [email protected] 3 Elements Named for their number of protons X = element symbol Z (atomic number) = number of protons in nucleus N = number of neutrons in nucleus A A A A (atomic mass number) = Z + N Z X N Z X X [A is different than, but approximately equal to the atomic weight of an atom in amu] Examples; oxygen, lead A Electrically neural atom, Z X N has Z electrons in its 16 208 atomic orbit.
    [Show full text]
  • Double-Beta Decay of 96Zr and Double-Electron Capture of 156Dy to Excited Final States
    Double-Beta Decay of 96Zr and Double-Electron Capture of 156Dy to Excited Final States by Sean W. Finch Department of Physics Duke University Date: Approved: Werner Tornow, Supervisor Calvin Howell Kate Scholberg Berndt Mueller Albert Chang Dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the Department of Physics in the Graduate School of Duke University 2015 Abstract Double-Beta Decay of 96Zr and Double-Electron Capture of 156Dy to Excited Final States by Sean W. Finch Department of Physics Duke University Date: Approved: Werner Tornow, Supervisor Calvin Howell Kate Scholberg Berndt Mueller Albert Chang An abstract of a dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the Department of Physics in the Graduate School of Duke University 2015 Copyright c 2015 by Sean W. Finch All rights reserved except the rights granted by the Creative Commons Attribution-Noncommercial License Abstract Two separate experimental searches for second-order weak nuclear decays to excited final states were conducted. Both experiments were carried out at the Kimballton Underground Research Facility to provide shielding from cosmic rays. The first search is for the 2νββ decay of 96Zr to excited final states of the daughter nucleus, 96Mo. As a byproduct of this experiment, the β decay of 96Zr was also investigated. Two coaxial high-purity germanium detectors were used in coincidence to detect γ rays produced by the daughter nucleus as it de-excited to the ground state. After collecting 1.92 years of data with 17.91 g of enriched 96Zr, half-life limits at the level of 1020 yr were produced.
    [Show full text]
  • Nuclear Chemistry Why? Nuclear Chemistry Is the Subdiscipline of Chemistry That Is Concerned with Changes in the Nucleus of Elements
    Nuclear Chemistry Why? Nuclear chemistry is the subdiscipline of chemistry that is concerned with changes in the nucleus of elements. These changes are the source of radioactivity and nuclear power. Since radioactivity is associated with nuclear power generation, the concomitant disposal of radioactive waste, and some medical procedures, everyone should have a fundamental understanding of radioactivity and nuclear transformations in order to evaluate and discuss these issues intelligently and objectively. Learning Objectives λ Identify how the concentration of radioactive material changes with time. λ Determine nuclear binding energies and the amount of energy released in a nuclear reaction. Success Criteria λ Determine the amount of radioactive material remaining after some period of time. λ Correctly use the relationship between energy and mass to calculate nuclear binding energies and the energy released in nuclear reactions. Resources Chemistry Matter and Change pp. 804-834 Chemistry the Central Science p 831-859 Prerequisites atoms and isotopes New Concepts nuclide, nucleon, radioactivity, α− β− γ−radiation, nuclear reaction equation, daughter nucleus, electron capture, positron, fission, fusion, rate of decay, decay constant, half-life, carbon-14 dating, nuclear binding energy Radioactivity Nucleons two subatomic particles that reside in the nucleus known as protons and neutrons Isotopes Differ in number of neutrons only. They are distinguished by their mass numbers. 233 92U Is Uranium with an atomic mass of 233 and atomic number of 92. The number of neutrons is found by subtraction of the two numbers nuclide applies to a nucleus with a specified number of protons and neutrons. Nuclei that are radioactive are radionuclides and the atoms containing these nuclei are radioisotopes.
    [Show full text]
  • Chapter 16 Nuclear Chemistry
    Chapter 16 275 Chapter 16 Nuclear Chemistry Review Skills 16.1 The Nucleus and Radioactivity Nuclear Stability Types of Radioactive Emissions Nuclear Reactions and Nuclear Equations Rates of Radioactive Decay Radioactive Decay Series The Effect of Radiation on the Body 16.2 Uses of Radioactive Substances Medical Uses Carbon-14 Dating Other Uses for Radioactive Nuclides 16.3 Nuclear Energy Nuclear Fission and Electric Power Plants Nuclear Fusion and the Sun Special Topic 16.1: A New Treatment for Brain Cancer Special Topic 16.2: The Origin of the Elements Chapter Glossary Internet: Glossary Quiz Chapter Objectives Review Questions Key Ideas Chapter Problems 276 Study Guide for An Introduction to Chemistry Section Goals and Introductions Section 16.1 The Nucleus and Radioactivity Goals To introduce the new terms nucleon, nucleon number, and nuclide. To show the symbolism used to represent nuclides. To explain why some nuclei are stable and others not. To provide you with a way of predicting nuclear stability. To describe the different types of radioactive decay. To show how nuclear reactions are different from chemical reactions. To show how nuclear equations are different from chemical equations. To show how the rates of radioactive decay can be described with half-life. To explain why short-lived radioactive atoms are in nature. To describe how radiation affects our bodies.. This section provides the basic information that you need to understand radioactive decay. It will also help you understand the many uses of radioactive atoms, including how they are used in medicine and in electricity generation. Section 16.2 Uses of Radioactive Substances Goal: To describe many of the uses of radioactive atoms, including medical uses, archaeological dating, smoke detectors, and food irradiation.
    [Show full text]
  • Enhancement Mechanisms of Low Energy Nuclear Reactions
    Enhancement Mechanisms of Low Energy Nuclear Reactions Gareev F.A., Zhidkova I.E. Joint Institute for Nuclear Research, 141980, Dubna, Russia [email protected] [email protected] 1 Introduction One of the fundamental presentations of nuclear physics since the very early days of its study has been the common assumption that the radioactive process (the half-life or decay constant) is independent of external conditions. Rutherford, Chadwick and Ellis [1] came to the conclusion that: • ≪the value of λ (the decay constant) for any substance is a characteristic constant inde- pendent of all physical and chemical conditions≫. This very important conclusion (still playing a negative role in cold fusion phenomenon) is based on the common expectation (P. Curie suggested that the decay constant is the etalon of time) and observation that the radioactivity is a nuclear phenomenon since all our actions affect only states of the atom but do not change the nucleus states. We cannot hope to mention even a small part of the work done to establish the constancy of nuclear decay rates. For example, Emery G.T. stated [2]: • ≪Early workers tried to change the decay constants of various members of the natural radioactive series by varying the temperature between 24◦K and 1280◦K, by applying pressure of up to 2000 atm, by taking sources down into mines and up to the Jungfraujoch, by applying magnetic fields of up to 83,000 Gauss, by whirling sources in centrifuges, and by many other ingenious techniques. Occasional positive results were usually understood, arXiv:nucl-th/0505021v1 8 May 2005 in time, as result of changes in the counting geometry, or of the loss of volatile members of the natural decay chains.
    [Show full text]
  • International Symposium on Ion-Atom Collisions
    Double-electron capture in low-energy H+ + H− collisions Y Wu1,2*, JW Gao1,3†,J G Wang1, A Dubois3 and N Sisourat3 1Institute of Applied Physics and Computational Mathematics, 100088 Beijing, China 2HEDPS, Center for Applied Physics and Technology, Peking University, 100084 Beijing, China 3Sorbonne Universitè, CNRS, Laboratoire de Chimie Physique-Matière et Rayonnement, F-75005 Paris, France Synopsis In this talk, I shall present our latest work [1] on the double-electron capture process in the H+-H- collision in the low energy range, from 60 eV to 20 keV. A fully correlated two-active-electron semi-classical atomic-orbital close-coupling approach (AOCC) is employed, using a large basis set ensuring a reasonable con- vergence in the whole energy domain. Our results reproduce well the experimental data for the first time in both magnitude and shape. Furthermore, the oscillation structures phenomenon observed in the experiments has been interpreted as coherence effects between double electron capture and the transfer-excitation processes. In ion-atom/molecule collisions, one-electron clear oscillatory structure whose period increases processes for systems such as H+ + H [2] and He2+ with increasing impact energies. It is demonstrated + + H2 [3], have been fairly well understood [4], to be stem from coherence effects between double while the knowledge on multi-electron ones is still electron capture and other two-electron inelastic far from complete. As a benchmark of double elec- channels (transfer-excitation). From the view of a tron collision system, H+ + H− collision has been molecular picture, the oscillation period can be well extensively investigated for more than five decades.
    [Show full text]
  • Comments on Evaluation of Al Electron-Capture and Positron
    26 Comments on evaluation – CEA ISBN 2 7272 0211 3 Al Comments on evaluation of 26Al Electron-Capture and Positron Decay Data by Shiu-Chin Wu and E. Browne The Limitation of Relative Statistical Weight [2] (LWM) method, used for averaging numbers throughout this evaluation, provided a uniform approach for the analysis of discrepant data. The uncertainty assigned to the recommended values was always greater than or equal to the smallest uncertainty of the values used to calculate the average. Decay Scheme 26Al decays 100% by EC + b+ to 26Mg 2+ states at 1808.72 and 2938.41 keV. A measured relative emission probability for the positron annihilation radiation (511 keV) produced a total b+ branching of 82(2)% (72Sa02). This branching agrees well with a value of 81.7% predicted by theory[1]. Nuclear Data The recommended half-life of 26Al, 7.17(24) ´ 105 y, is a weighted average (c2/N-1=0.64, LWM) of 5 + 5 + 7.16(32) ´ 10 y, from partial T1/2 (b )= 8.73(30) ´ 10 y, b counting and mass spectrometric analysis [3], combined with b+(%)=82(2) from measurement of positron annihilation radiation (72Sa02)); 7.05(24) ´ 105 y, by specific activity and mass spectrometric analysis [4]; 7.8 (5) ´ 105 y, by specific activity from a source produced by 26Mg(p,n) 26Al (the number of 26Al atoms in the source were estimated by using the reaction cross section) [5]; and 7.02 (56) ´ 105 y, by counting the atoms of 26Al that did not disintegrate in the source (Accelerator Mass Spectrometry) [6].
    [Show full text]
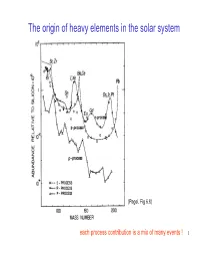
  • The Origin of Heavy Elements in the Solar System
    The origin of heavy elements in the solar system (Pagel, Fig 6.8) each process contribution is a mix of many events ! 1 Abundance pattern: “Finger print ” of the r-process ? Tellurium and Xenon Peak Platinum Peak Solar abundance of the elements r-process only (subtract s,p processes) ) 6 Abundance (Si(Si = =Abundance Abundance 10 10 Element number (Z) But: sun formed ~10 billion years after big bang: many stars contributed to elements This could be an accidental combination of many different “fingerprints ” ? Find a star that is much older than the sun to find “fingerprint ” of single event 2 Heavy elements in Metal Poor Halo Stars CS22892-052 red (K) giant located in halo distance: 4.7 kpc mass ~0.8 M_sol [Fe/H]= −−−3.0 recall: [Dy/Fe]= +1.7 [X/Y]=log(X/Y)-log(X/Y) solar old stars - formed before Galaxy was mixed they preserve local pollution from individual nucleosynthesis events 3 A single (or a few) r -process event(s) CS22892-052 (Sneden et al. 2003) 1 solar r Cosmo Chronometer 0 -1 NEW: CS31082-001 with U (Cayrel et al. 2001) -2 40 50 60 70 80 90 Age: 16+ - 3 Gyr element number (Schatz et al. 2002 other, second ApJ 579, 626) r-process to fill main r-process this up ? matches exactly solar r-pattern (weak r-process) conclusions ? 4 More rII stars Solar r-process elements from many events J. Cowan 5 A surprise J. Cowan A new process contributing to Y, Sr, Zr (early Galaxy only? Solar? In this case: some traditional “r-contributions” to solar are not (main) r-process) Call it LEPP (Light Element Primary Process) 6 Overview heavy
    [Show full text]