Knowledge Discovery with Bayesian Networks Li
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

CONVERGENCE OR COLLISION? Navigating the Creative, Commercial and Regulatory Challenges Facing Media Over the Next Decade
WEDNESDAY 19 JANUARY 2011 SAÏD BUSINESS SCHOOL, UNIVERSITY OF OXFORD CONVERGENCE OR COLLISION? Navigating the creative, commercial and regulatory challenges facing media over the next decade guardian.co.uk/oxfordmediaconvention Event partner Event organisers PROGRAMME 08:50 REGISTRATION AND COFFEE 09:45 INTRODUCTION AND WELCOME Nick Pearce, director, ippr 09:50 A CITIZEN’S COMMUNICATION ACT: WHAT THE PUBLIC WANT FROM OUR MEDIA A short vox pop film 10:00 KEYNOTE SPEECH MEDIA POLICY: THE COALITION’S 10 YEAR PLAN Rt Hon Jeremy Hunt MP, secretary of state, culture, Olympics, media and sport 10:40 PLENARY PANEL MEDIA 2011: WHAT NEEDS TO CHANGE? A conversation between the public and providers In this, the Oxford Media Convention’s ninth year, we ask a panel of public representatives and a panel of providers to discuss and debate the current and future course of Britain’s media and creative industries. • How will public service provision, diversity, plurality and media literacy be preserved and promoted over the next decade? • How can public and private entities secure the UK’s position in the global media market place? • What does the future look like? How will audiences be consuming content, how will businesses be making money and what role will government have in shaping media policy and facilitating the creation of growth and infrastructure? In little over an hour and a half can these figures plot out a blueprint for creating an effective environment for growth and public provision? Moderator: Jon Snow, presenter, Channel 4 News Panel 1: Dawn Airey, president, CLT-UFA UK TV (part of the RTL Group) Richard Halton, chief executive, YouView Ashley Highfield, managing director & vice president, consumer & online UK, Microsoft Caroline Thomson, chief operating officer, BBC Panel 2: Sam Conniff, co-founder, Livity Mark Damazer, master, St. -
Channel Guide August 2018
CHANNEL GUIDE AUGUST 2018 KEY HOW TO FIND WHICH CHANNELS YOU HAVE 1 PLAYER PREMIUM CHANNELS 1. Match your ENTERTAINMENT package 1 2 3 4 5 6 2 MORE to the column 100 Virgin Media Previews 3 M+ 101 BBC One If there’s a tick 4 MIX 2. 102 BBC Two in your column, 103 ITV 5 FUN you get that 104 Channel 4 6 FULL HOUSE channel ENTERTAINMENT SPORT 1 2 3 4 5 6 1 2 3 4 5 6 100 Virgin Media Previews 501 Sky Sports Main Event 101 BBC One HD 102 BBC Two 502 Sky Sports Premier 103 ITV League HD 104 Channel 4 503 Sky Sports Football HD 105 Channel 5 504 Sky Sports Cricket HD 106 E4 505 Sky Sports Golf HD 107 BBC Four 506 Sky Sports F1® HD 108 BBC One HD 507 Sky Sports Action HD 109 Sky One HD 508 Sky Sports Arena HD 110 Sky One 509 Sky Sports News HD 111 Sky Living HD 510 Sky Sports Mix HD 112 Sky Living 511 Sky Sports Main Event 113 ITV HD 512 Sky Sports Premier 114 ITV +1 League 115 ITV2 513 Sky Sports Football 116 ITV2 +1 514 Sky Sports Cricket 117 ITV3 515 Sky Sports Golf 118 ITV4 516 Sky Sports F1® 119 ITVBe 517 Sky Sports Action 120 ITVBe +1 518 Sky Sports Arena 121 Sky Two 519 Sky Sports News 122 Sky Arts 520 Sky Sports Mix 123 Pick 521 Eurosport 1 HD 132 Comedy Central 522 Eurosport 2 HD 133 Comedy Central +1 523 Eurosport 1 134 MTV 524 Eurosport 2 135 SYFY 526 MUTV 136 SYFY +1 527 BT Sport 1 HD 137 Universal TV 528 BT Sport 2 HD 138 Universal -

Discovery Communications to Launch First Channel on Freeview in UK
Discovery Communications to Launch First Channel on Freeview in UK October 17, 2008 - Company Wins Competitive Auction for Position on SDN Multiplex - LONDON, Oct. 17 /PRNewswire-FirstCall/ -- Discovery Communications today announced it has secured a channel position on Freeview, the UK's digital terrestrial television (DTT) platform. The deal with UK multiplex operator, SDN Ltd, a wholly owned subsidiary of ITV plc, will see the channel launch in early 2009. (Logo: http://www.newscom.com/cgi-bin/prnh/20080918/NETH035LOGO ) The channel will draw upon Discovery Communications' vast library of high-quality factual, entertainment and lifestyle programming and also includes scripted acquisitions especially for the new channel. Discovery Communications launched its first international channel in the UK in 1989. The UK business has grown to a robust portfolio of 11 pay-TV channels available through SKY, Virgin Media and other platforms. David Zaslav, president and CEO of Discovery Communications, said, "Discovery Communications is very proud to bring its first channel to Freeview. Our first international channel launched in the UK nearly 20 years ago and the company always has been 'platform neutral' in its distribution strategy. Discovery Communications' Freeview channel will both complement and enhance our offerings and portfolio position in the critical UK market." Dan Brooke, managing director of Discovery Networks UK, added, "The UK now has the most competitive and diverse TV market in the world and the launch of a Freeview channel is an important element in expanding consumer reach. We have talked to Freeview viewers: they love our programming, and once they have sampled it, we are confident they will want to experience the richness and variety of our content on other media platforms." Jeff Henry, managing director, ITV Consumer, said: "SDN is delighted to be working with Discovery Communications to enhance Freeview's channel offering even further. -

SIMPLESTREAM SECURES FURTHER £2M FUNDING to GROW INTERNATIONALLY and ROLLOUT TVPLAYER Submitted By: Simplestream Thursday, 5 February 2015
SIMPLESTREAM SECURES FURTHER £2m FUNDING TO GROW INTERNATIONALLY AND ROLLOUT TVPLAYER Submitted by: SimpleStream Thursday, 5 February 2015 LONDON, 5th February 2015 – Simplestream, a leading provider of ‘Over-the-Top’ (OTT) live streaming services for broadcast TV channels, is pleased to announce it has secured an additional £2m in equity funding from a consortium including Beringea, a leading growth capital firm with a focus on media and technology companies, and YOLO Leisure and Technology, an AIM listed investment company. The investment will accelerate the expansion of Simplestream’s video streaming platform in the UK and internationally, and the continued development of TVPlayer, Simplestream’s B2C live TV streaming service, which is to be made available on a white-label basis. Simplestream is a leading provider of live streaming and live-to-VOD services, whose broadcast clients include Discovery Networks, Scripps Networks, Box Television, QVC, At The Races and Turner Broadcasting amongst others. Simplestream’s cloud-based Media Manager solution enables broadcasters to securely live stream broadcast content to any device with minimal latency and gain significant workflow efficiencies through the automated creation of multi-bitrate, multi-platform video files from the live stream. The generation of long-form “catchup” programming, with or without ad-breaks, and the creation of short-form video clips are supported via a single system. Such is the growth in demand for live streaming services; Simplestream has seen 100% revenue growth year on year since its Media Manager was introduced to the UK market in 2012. The company now delivers services across Europe and North America, with a focus on sport, music, news, faith and teleshopping channels. -

Highlights December 2012
If you do not currently receive our monthly highlights and would like to, please email: [email protected] Click here for press office contacts Click on logo to go directly to channel Highlights December 2012 Ben Fogle has battled scorching sands in the they try their hand at the ultimate rock climbing Sahara, taken on the seas to row the Atlantic and experience at the world famous Castleton Tower Ben Fogle’s has crossed the frozen wastes of the Antarctic in Utah. Along the way Ben will even tackle his to reach the South Pole. Now, he’s ready for his personal fears of heights with adventures such next mission as he explores the world’s greatest as cliff diving as well as a solo skydive from Year of Adventures adventures. He will take himself to towering 10,000 feet. In the first episode Ben heads to the heights and down to plunging lows as well as to Australian wilderness to take part in the world’s UK SERIES PREMIERE extreme regions where temperatures soar and largest adventure race, where he will run, bike, THURSDAYS FROM 7TH FEBRUARY, 9.00PM never see the light of day. Although all of his swim and kayak to the finishing line. To prepare he exploits are spectacular and breath taking, he is takes on an urban assault course in London and determined that they will all be adventures that attempts to swim from the infamous island prison anyone can experience. of Alcatraz in San Francisco. With his enthusiasm and determination, this action packed series is all Ben embarks on a series of challenges all across about the voyage into the unknown, facing fear the world, from ice climbing and scuba diving in and the thrill of the new. -

TV & Radio Channels Astra 2 UK Spot Beam
UK SALES Tel: 0345 2600 621 SatFi Email: [email protected] Web: www.satfi.co.uk satellite fidelity Freesat FTA (Free-to-Air) TV & Radio Channels Astra 2 UK Spot Beam 4Music BBC Radio Foyle Film 4 UK +1 ITV Westcountry West 4Seven BBC Radio London Food Network UK ITV Westcountry West +1 5 Star BBC Radio Nan Gàidheal Food Network UK +1 ITV Westcountry West HD 5 Star +1 BBC Radio Scotland France 24 English ITV Yorkshire East 5 USA BBC Radio Ulster FreeSports ITV Yorkshire East +1 5 USA +1 BBC Radio Wales Gems TV ITV Yorkshire West ARY World +1 BBC Red Button 1 High Street TV 2 ITV Yorkshire West HD Babestation BBC Two England Home Kerrang! Babestation Blue BBC Two HD Horror Channel UK Kiss TV (UK) Babestation Daytime Xtra BBC Two Northern Ireland Horror Channel UK +1 Magic TV (UK) BBC 1Xtra BBC Two Scotland ITV 2 More 4 UK BBC 6 Music BBC Two Wales ITV 2 +1 More 4 UK +1 BBC Alba BBC World Service UK ITV 3 My 5 BBC Asian Network Box Hits ITV 3 +1 PBS America BBC Four (19-04) Box Upfront ITV 4 Pop BBC Four (19-04) HD CBBC (07-21) ITV 4 +1 Pop +1 BBC News CBBC (07-21) HD ITV Anglia East Pop Max BBC News HD CBeebies UK (06-19) ITV Anglia East +1 Pop Max +1 BBC One Cambridge CBeebies UK (06-19) HD ITV Anglia East HD Psychic Today BBC One Channel Islands CBS Action UK ITV Anglia West Quest BBC One East East CBS Drama UK ITV Be Quest Red BBC One East Midlands CBS Reality UK ITV Be +1 Really Ireland BBC One East Yorkshire & Lincolnshire CBS Reality UK +1 ITV Border England Really UK BBC One HD Channel 4 London ITV Border England HD S4C BBC One London -

016Cd9e416e4569af696511dd3
The current issue and full text archive of this journal is available on Emerald Insight at: www.emeraldinsight.com/2056-4945.htm AAM “ ” 5,2 Show us your moves : trade rituals of television marketing Paul Grainge and Catherine Johnson 126 Department of Culture, Film and Media, University of Nottingham, Nottingham, UK Received 25 June 2014 Revised 5 September 2014 Abstract Accepted 20 November 2014 Purpose – The purpose of this paper is to examine the professional culture of television marketing in the UK, the sector of arts marketing responsible for the vast majority of programme trailers and channel promos seen on British television screens. Design/methodology/approach – In research approach, it draws on participant observation at Promax UK, the main trade conference and award ceremony of the television marketing community. Developing John Caldwell’s analysis of the cultural practices of worker groups, it uses Promax as a site of study itself, exploring how a key trade gathering forges, legitimates and ritualizes the identity and practice of those involved in television marketing. Findings – Its findings show how Promax transmits industrial lore, not only about “how to do” the job of television marketing but also “how to be” in the professional field. If trade gatherings enable professional communities to express their own values to themselves, Promax members are constructed as “TV people” rather than just “marketing people”; the creative work of television marketing is seen as akin to the creative work of television production and positioned as part of the television industry. Originality/value – The value of the paper is the exploration of television marketing as a professional and creative discipline. -

Basic-Cable-Channels.Pdf
TV INSTRUCTIONS You do not need a cable box to access these channels, you should be able to plug your TV directly into the wall with a standard coaxial cable* and begin watching. Not getting any channels? Your TV must be equipped with an “HRC” digital tuner in order to receive these channels. Most TV’s manufactured after 2010 have this tuner, however, there are some that do not. If you think your TV has an “HRC” digital tuner and you are not receiving any channels, please try the following steps: 1. Go to your Menu 2. Go to Options/Settings 3. Go to Tuner/Frequency 4. You should see different selections such as “Standard”/”HRC”/”IRC” 5. Select “HRC” 6. Run a channel scan Please note, the channels will look like decimal points rather than normal channel numbers. If you are still unsuccessful after trying these steps, please contact your RSO for further assistance. *Cable cords are not provided by UCR Housing, and may need to be purchased. UC RIVERSIDE Digital chANNEL gUIdE SD Digital Direct ChDHD Digital irect Ch HD Digital Direct Ch 3Government Access 21-606 2KCBS - CBS 12-41280Hallmark Channel50-873 14 KTBN - TBN 20-594KNBC - NBC 11-40282Turner Classic Movies 10-887 15 KILM - IND 25-4545KTLA - CW 13-42183LMN 51-880 18 KSCI - IND 20-527 6KMEX - UNV 22-47084OWN 51-913 19 KRCA - Estrella 20-530 7KABC - ABC 23-43185 Oxygen 51-883 20 KXLA - IND 19-503 8QVC 31-7 62 fx 9-841 21 KVMD - IND 19-502 9KCAL - IND 12-41163 BET 49-875 24 KVCR - PBS 25-455 10 KDOC - IND 24-44264Comedy Central28-862 25 KLCS - PBS 20-526 11 KTTV - FOX 13-42265 Nickelodeon-West -

Estudio Sobre El Mercado De Servicios De Televisión
hdrb ESTUDIO SOBRE EL MER CADO DE SERVICIOS DE TELEVISIÓN ABIE RTA EN MÉXICO COMISIÓN FEDERAL DE TE LECOMUNICACIONES “ Condiciones del mercado de televisión abierta en México” MÉXICO D.F., SEPTIEMBRE DE 2011 ÍNDICE RESUMEN EJECUTIVO .......................................................................................................................... 2 INTRODUCCIÓN ................................................................................................................................. 13 CONDICIONES DEL MERCADO DE LA TELEVISIÓN ABIERTA EN MÉXICO ........................................... 16 CRÓNICA DE LAS CONCESIONES OTORGADAS .................................................................................. 18 OFERTA .............................................................................................................................................. 23 Televisión abierta pública ............................................................................................................. 24 Televisión abierta privada ............................................................................................................. 25 Televisión de paga ......................................................................................................................... 27 El futuro de la televisión ............................................................................................................... 28 DEMANDA ........................................................................................................................................ -

GEITF Programme 2010.Pdf
MediaGuardian Edinburgh International Television Festival 27–29 August 2010 Programme of Events ON TV Contents Welcome to Edinburgh 02 Schedule at a Glance 28 Social Events 06 Friday Sessions 20 Friday Night Opening Reception / Saturday Meet Highlights include: TV’s Got to Dance / This is England and Greet / Saturday Night Party / Channel of the ‘86 plus Q&A / The Richard Dunn Memorial Lecture: Year Awards Jimmy Mulville / The James MacTaggart Memorial Lecture: Mark Thompson Sponsors 08 Saturday Sessions 30 Information 13 Extras 14 Workshops 16 EICC Orientation Guide 18 Highlights include: 50 Years of Coronation Street: A Masterclass / The Alternative MacTaggart: Paul Abbott / Venues 19 The Futureview: Sandy Climan / EastEnders at 25: A Masterclass The Network 44 Sunday Sessions 40 Fast Track 46 Executive Committee 54 Advisory Committee 55 Festival Team 56 Highlights include: Doctor Who: A Masterclass / Katie Price: Shrink Rap / The Last Laugh Keynote Speaker Biographies 52 Mark Thompson / Paul Abbott / Jimmy Mulville / Sandy Climan Welcome to Edinburgh man they call “Hollywood’s Mr 3D” Sandy Climan bacon sarnies. The whole extravaganza will be for this year's Futureview keynote to answer the hosted by Mark Austin who will welcome guests DEFINING question Will it Go Beyond Football, Films and onto his own Sunday morning sofa. Michael Grade F****ng?. In a new tie-up between the TV Festival will give us his perspective on life in his first public and the Edinburgh Interactive Festival we’ve appearance since leaving ITV. Steven Moffat will THE YEAR’S brought together the brightest brains from the be in conversation in a Doctor Who Masterclass. -

Media Nations 2020 UK Report
Media Nations 2020 UK report Published 5 August 2020 Contents Section Overview 3 1. Covid-19 media trends: consumer behaviour 6 2. Covid-19 media trends: industry impact and response 44 3. Production trends 78 4. Advertising trends 90 2 Media Nations 2020 Overview This is Ofcom’s third annual Media Nations, a research report for industry, policy makers, academics and consumers. It reviews key trends in the TV and online video sectors, as well as radio and other audio sectors. Accompanying this report is an interactive report that includes an extensive range of data. There are also separate reports for Northern Ireland, Scotland and Wales. This year’s publication comes during a particularly eventful and challenging period for the UK media industry. The Covid-19 pandemic and the ensuing lockdown period has changed consumer behaviour significantly and caused disruption across broadcasting, production, advertising and other related sectors. Our report focuses in large part on these recent developments and their implications for the future. It sets them against the backdrop of longer-term trends, as laid out in our five-year review of public service broadcasting (PSB) published in February, part of our Small Screen: Big Debate review of public service media. Media Nations provides further evidence to inform this, as well as assessing the broader industry landscape. We have therefore dedicated two chapters of this report to analysis of Covid-19 media trends, and two chapters to wider market dynamics in key areas that are shaping the industry: • The consumer behaviour chapter examines the impact of the Covid-19 pandemic on media consumption trends across television and online video, and radio and online audio. -
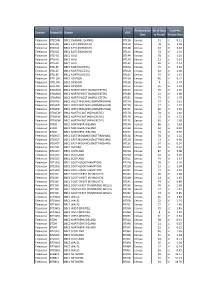
Broadcast Website Info D183 MCPS.Xlsx
Performance No of Days Total Per Domain Station IDStation UDC Date in Period Minute Rate Television BT1CHN BBC1 CHANNEL ISLANDS BT11A Census 51£ 0.11 Television BT1EAS BBC1 EAST (NORWICH) BT12A Census 78£ 3.04 Television BT1EAS BBC1 EAST (NORWICH) BT12B Census 13£ 2.18 Television BT1EAS BBC1 EAST (NORWICH) BT12C Census 74£ 1.31 TelevisionBT1HUL BBC1 HULL BT14A Census 78£ 0.33 TelevisionBT1HUL BBC1 HULL BT14B Census 13£ 0.24 TelevisionBT1HUL BBC1 HULL BT14C Census 65£ 0.14 Television BT1LEE BBC1 NORTH (LEEDS) BT16A Census 77£ 3.32 Television BT1LEE BBC1 NORTH (LEEDS) BT16B Census 12£ 2.38 Television BT1LEE BBC1 NORTH (LEEDS) BT16C Census 74£ 1.42 Television BT1LON BBC1 LONDON BT15A Census 46£ 5.22 Television BT1LON BBC1 LONDON BT15B Census 4£ 3.74 Television BT1LON BBC1 LONDON BT15C Census 65£ 2.24 Television BT1MAN BBC1 NORTH WEST (MANCHESTER) BT18A Census 78£ 4.16 Television BT1MAN BBC1 NORTH WEST (MANCHESTER) BT18B Census 13£ 2.98 Television BT1MAN BBC1 NORTH WEST (MANCHESTER) BT18C Census 73£ 1.79 Television BT1MID BBC1 WEST MIDLANDS (BIRMINGHAM) BT27A Census 74£ 3.23 Television BT1MID BBC1 WEST MIDLANDS (BIRMINGHAM) BT27B Census 12£ 2.32 Television BT1MID BBC1 WEST MIDLANDS (BIRMINGHAM) BT27C Census 60£ 1.39 Television BT1NEW BBC1 NORTH EAST (NEWCASTLE) BT17A Census 78£ 2.40 Television BT1NEW BBC1 NORTH EAST (NEWCASTLE) BT17B Census 13£ 1.72 Television BT1NEW BBC1 NORTH EAST (NEWCASTLE) BT17C Census 65£ 1.03 Television BT1NI BBC1 NORTHERN IRELAND BT19A Census 86£ 1.29 Television BT1NI BBC1 NORTHERN IRELAND BT19B Census 33£ 0.92 Television