Four-Component Relativistic Density-Functional Theory Calculations of Nuclear Spin–Rotation Constants: Relativistic Effects in P-Block Hydrides
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

1 9729/01/TJC Prelim/2018 [Turn Over
1 CHEMISTRY 9729/01 Paper 1 Multiple Choice 15th September 2018 1 hour Additional materials: Multiple Choice Answer Sheet Data Booklet READ THESE INSTRUCTIONS FIRST Write in soft pencil. Do not use staples, paper clips, glue or correction fluid. Write your name and Civics Group Write and shade your index number There are thirty questions on this paper. Answer all questions. For each question there are four possible answers A, B, C and D. Choose the one you consider correct and record your choice in soft pencil on the separate Answer Sheet. Read the instructions on the Answer Sheet very carefully. Each correct answer will score one mark. A mark will not be deducted for a wrong answer. Any rough working should be done in this booklet. The use of an approved scientific calculator is expected, where appropriate. This document consists of 13 printed pages. 9729/01/TJC Prelim/2018 [Turn Over 2 Section A For each question there are four possible answers, A, B, C and D. Choose the one you consider correct and record your choice in soft pencil on the separate Answer Sheet (OMS). 1 Some isotopes are unstable and undergo nuclear (radioactive) reactions. In one type of reaction, an unstable nucleus assimilates an electron from an inner orbital of its electron cloud. The net effect is the conversion of a proton and an electron into a neutron. Which of the following describes this type of reaction? A 11C 12C B 111I 111Te C 76Br 75Br D 76Kr 75Br 2 Sodium hydrogencarbonate can be prepared from sodium sulfate by a three-step process: Na2SO4(s) + 4C(s) -

Inorganic Chemistry
AS-Level INORGANIC CHEMISTRY Q1 A mixture of the oxides of two elements of the third period is dissolved in water. The solution is approximately neutral. What could be the constituents of the mixture? A Al2O3 and MgO B Na2O and MgO C Na2O and P4O10 D SO3 and P4O10 Q2 Aluminium chloride catalyses certain reactions by forming carbocations (carbonium ions) with chloroalkanes as shown. Which property makes this reaction possible? A AlCl3 is a covalent molecule. B AlCl3 exists as the dimer Al2Cl6 in the vapour. C The aluminium atom in AlCl3 has an incomplete octet of electrons. D The chlorine atom in RCl has a vacant p orbital. Q3 What are the products of the thermal decomposition of magnesium nitrate? A magnesium nitride and oxygen B magnesium oxide and nitrogen C magnesium oxide, nitrogen and oxygen D magnesium oxide, nitrogen dioxide and oxygen Q4 Chlorine compounds show oxidation states ranging from –1 to +7. What are the reagent(s) and conditions necessary for the oxidation of elemental chlorine into a compound containing chlorine in the +5 oxidation state? A AgNO3(aq) followed by NH3(aq) at room temperature B concentrated H2SO4 at room temperature C cold dilute NaOH(aq) D hot concentrated NaOH(aq) Q5 Which gaseous hydride most readily decomposes into its elements on contact with a hot glass rod? A ammonia B hydrogen chloride C hydrogen iodide D steam Q6 Which reagent, when mixed and heated with ammonium sulphate, liberates ammonia? A aqueous bromine B dilute hydrochloric acid C limewater D acidified potassium dichromate(VI) Q7 Which pollutant -

WO 2016/074683 Al 19 May 2016 (19.05.2016) W P O P C T
(12) INTERNATIONAL APPLICATION PUBLISHED UNDER THE PATENT COOPERATION TREATY (PCT) (19) World Intellectual Property Organization International Bureau (10) International Publication Number (43) International Publication Date WO 2016/074683 Al 19 May 2016 (19.05.2016) W P O P C T (51) International Patent Classification: (81) Designated States (unless otherwise indicated, for every C12N 15/10 (2006.01) kind of national protection available): AE, AG, AL, AM, AO, AT, AU, AZ, BA, BB, BG, BH, BN, BR, BW, BY, (21) International Application Number: BZ, CA, CH, CL, CN, CO, CR, CU, CZ, DE, DK, DM, PCT/DK20 15/050343 DO, DZ, EC, EE, EG, ES, FI, GB, GD, GE, GH, GM, GT, (22) International Filing Date: HN, HR, HU, ID, IL, IN, IR, IS, JP, KE, KG, KN, KP, KR, 11 November 2015 ( 11. 1 1.2015) KZ, LA, LC, LK, LR, LS, LU, LY, MA, MD, ME, MG, MK, MN, MW, MX, MY, MZ, NA, NG, NI, NO, NZ, OM, (25) Filing Language: English PA, PE, PG, PH, PL, PT, QA, RO, RS, RU, RW, SA, SC, (26) Publication Language: English SD, SE, SG, SK, SL, SM, ST, SV, SY, TH, TJ, TM, TN, TR, TT, TZ, UA, UG, US, UZ, VC, VN, ZA, ZM, ZW. (30) Priority Data: PA 2014 00655 11 November 2014 ( 11. 1 1.2014) DK (84) Designated States (unless otherwise indicated, for every 62/077,933 11 November 2014 ( 11. 11.2014) US kind of regional protection available): ARIPO (BW, GH, 62/202,3 18 7 August 2015 (07.08.2015) US GM, KE, LR, LS, MW, MZ, NA, RW, SD, SL, ST, SZ, TZ, UG, ZM, ZW), Eurasian (AM, AZ, BY, KG, KZ, RU, (71) Applicant: LUNDORF PEDERSEN MATERIALS APS TJ, TM), European (AL, AT, BE, BG, CH, CY, CZ, DE, [DK/DK]; Nordvej 16 B, Himmelev, DK-4000 Roskilde DK, EE, ES, FI, FR, GB, GR, HR, HU, IE, IS, IT, LT, LU, (DK). -

Characterization of At- Species in Simple and Biological Media by High Performance Anion Exchange Chromatography Coupled to Gamma Detector
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by HAL-Univ-Nantes Characterization of At- species in simple and biological media by high performance anion exchange chromatography coupled to gamma detector. A. Sabati´e-Gogova, Julie Champion, Sandrine Huclier, N. Michel, F. Pottier, N. Galland, Z. Asfari, M. Ch´erel,Gilles Montavon To cite this version: A. Sabati´e-Gogova, Julie Champion, Sandrine Huclier, N. Michel, F. Pottier, et al.. Charac- terization of At- species in simple and biological media by high performance anion exchange chromatography coupled to gamma detector.. Analytica Chimica Acta, Elsevier Masson, 2012, 721, pp.182. <10.1016/j.aca.2012.01.052>. <in2p3-00681129> HAL Id: in2p3-00681129 http://hal.in2p3.fr/in2p3-00681129 Submitted on 20 Mar 2012 HAL is a multi-disciplinary open access L'archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destin´eeau d´ep^otet `ala diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publi´esou non, lished or not. The documents may come from ´emanant des ´etablissements d'enseignement et de teaching and research institutions in France or recherche fran¸caisou ´etrangers,des laboratoires abroad, or from public or private research centers. publics ou priv´es. 1 Characterization of At- species in simple and biological media by high performance 2 anion exchange chromatography coupled to gamma detector. 3 4 5 A. Sabatié-Gogovaa, J. Championa, S. Hucliera, N. Michela, F. Pottiera, N. Gallandb, Z. 6 Asfaric, M. Chéreld, G. Montavona* 7 8 9 a Laboratoire SUBATECH, UMR CNRS 6457 IN2P3 Ecole des Mines de Nantes, 4 rue A. -
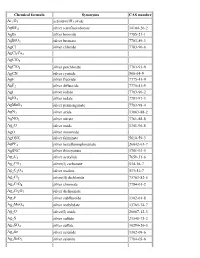
List of Chemical Formulas
Chemical formula Synonyms CAS number Ac2O3 actinium(III) oxide AgBF4 silver tetrafluoroborate 14104-20-2 AgBr silver bromide 7785-23-1 AgBrO3 silver bromate 7783-89-3 AgCl silver chloride 7783-90-6 AgCl3Cu2 AgClO3 AgClO4 silver perchlorate 7783-93-9 AgCN silver cyanide 506-64-9 AgF silver fluoride 7775-41-9 AgF2 silver difluoride 7775-41-9 AgI silver iodide 7783-96-2 AgIO3 silver iodate 7783-97-3 AgMnO4 silver permanganate 7783-98-4 AgN3 silver azide 13863-88-2 AgNO3 silver nitrate 7761-88-8 Ag2O silver oxide 1301-96-8 AgO silver monoxide AgONC silver fulminate 5610-59-3 AgPF6 silver hexafluorophosphate 26042-63-7 AgSNC silver thiocyanate 1701-93-5 Ag2C2 silver acetylide 7659-31-6 Ag2CO3 silver(I) carbonate 534-16-7 Ag2C2O4 silver oxalate 533-51-7 Ag2Cl2 silver(II) dichloride 75763-82-5 Ag2CrO4 silver chromate 7784-01-2 Ag2Cr2O7 silver dichromate Ag2F silver subfluoride 1302-01-8 Ag2MoO4 silver molybdate 13765-74-7 Ag2O silver(I) oxide 20667-12-3 Ag2S silver sulfide 21548-73-2 Ag2SO4 silver sulfate 10294-26-5 Ag2Se silver selenide 1302-09-6 Ag2SeO3 silver selenite 7784-05-6 Ag2SeO4 silver selenate 7784-07-8 Ag2Te silver(I) telluride 12002-99-2 Ag3Br2 silver dibromide 11078-32-3 Ag3Br3 silver tribromide 11078-33-4 Ag3Cl3 silver(III) trichloride 12444-96-1 Ag3I3 silver(III) triiodide 37375-12-5 Ag3PO4 silver phosphate 7784-09-0 AlBO aluminium boron oxide 12041-48-4 AlBO2 aluminium borate 61279-70-7 AlBr aluminium monobromide 22359-97-3 AlBr3 aluminium tribromide 7727-15-3 AlCl aluminium monochloride 13595-81-8 AlClF aluminium chloride fluoride -

GROUP 7 Halogen the Group of Halogens Is the Only Periodic Table
GROUP 7 Halogen The group of halogens is the only periodic table group that contains elements in all three familiar states of matter at standard temperature and pressure. All of the halogens form acids when bonded to hydrogen. Most halogens are typically produced from minerals of salts. The middle halogens, that is, chlorine, bromine and iodine, are often used as disinfectants. The halogens are also all toxic. Characteristics Chemical The halogens show trends in chemical bond energy moving from top to bottom of the periodic table column with fluorine deviating slightly. (It follows trend in having the highest bond energy in compounds with other atoms, but it has very weak bonds within the diatomic F2 element molecules.) Halogen bond energies (kJ/mol)[4] X X2 HX BX3 AlX3 CX4 F 159 574 645 582 456 Cl 243 428 444 427 327 Br 193 363 368 360 272 1 I 151 294 272 285 239 Halogens are highly reactive, and as such can be harmful or lethal to biological organisms in sufficient quantities. This high reactivity is due to the high electronegativity of the atoms due to their high effective nuclear charge. They can gain an electron by reacting with atoms of other elements. Fluorine is one of the most reactive elements in existence, attacking otherwise-inert materials such as glass, and forming compounds with the heavier noble gases. It is a corrosive and highly toxic gas. The reactivity of fluorine is such that, if used or stored in laboratory glassware, it can react with glass in the presence of small amounts of water to form silicon tetrafluoride (SiF4). -

2012-AJC-CH-H2-P1-Prelim.Pdf
ANDERSON JUNIOR COLLEGE Preliminary Examinations 2012 CHEMISTRY 9647/01 Higher 2 19 September 2012 Paper 1 Multiple Choice 1 hour Additional Materials: Multiple Choice Answer Sheet Data Booklet READ THESE INSTRUCTIONS FIRST Write in soft pencil. Do not use staples, paper clips, highlighters, glue or correction fluid. There are forty questions on this paper. Answer all questions. For each question there are four possible answers A, B, C and D. Choose the one you consider correct and record your choice in soft pencil on the Multiple Choice Answer Sheet. Each correct answer will score one mark. A mark will not be deducted for a wrong answer. Any rough working should be done in this booklet. Multiple Choice Answer Sheet Write your name, PDG and NRIC/FIN number, including the reference letter. Shade the NRIC / FIN number. Exam Title: JC 2 Prelim Exam Details: H2 Chem / Paper 1 Date: 19/09/2012 This document consists of 17 printed pages. AJC Prelim 2012 9647/01/H2 [Turn over 2 Section A For each question there are four possible answers, A, B, C and D. Choose the one you consider to be correct. 1 The first stage in the manufacture of nitric acid is the oxidation of ammonia by oxygen. aNH3(g) + bO2(g) cNO(g) + dH2O(g) What are the values for a, b, c and d? a b c d A 4 5 4 6 B 4 6 4 5 C 5 6 5 4 D 6 5 6 4 2 The nickel–cadmium rechargeable battery is based on the following overall reaction. -

(12) Patent Application Publication (10) Pub. No.: US 2011/0309017 A1 Hassler Et Al
US 2011 0309017A1 (19) United States (12) Patent Application Publication (10) Pub. No.: US 2011/0309017 A1 Hassler et al. (43) Pub. Date: Dec. 22, 2011 (54) METHODS AND DEVICES FOR ENHANCING CO2F I/44 (2006.01) CONTAMINANT REMOVAL BY RARE CO2F I/72 (2006.01) EARTHIS CO2F L/70 (2006.01) CO2F I/52 (2006.01) (75) Inventors: Carl R. Hassler, Gig Harbor, WA CO2F I/42 (2006.01) (US); John L. Burba, III, Parker, CO2F I/26 (2006.01) CO (US); Charles F. Whitehead, CO2F I/68 (2006.01) Henderson, NV (US); Joseph CO2F IOI/30 (2006.01) Lupo, Henderson, NV (US); CO2F IOI/2O (2006.01) Timothy L. Oriard, Issaquah, WA CO2F IOI/22 (2006.01) (US) CO2F IOI/12 (2006.01) CO2F IOI/14 (2006.01) (73) Assignee: MOLYCORP MINERALS, LLC, CO2F IOI/IO (2006.01) Greenwood Village, CO (US) CO2F IOI/38 (2006.01) CO2F IOI/16 (2006.01) (21) Appl. No.: 13/086,247 CO2F IOI/36 (2006.01) CO2F IOI/34 2006.O1 (22) Filed: Apr. 13, 2011 ( ) Related U.S. Application Data (52) U.S. Cl. ......... 210/638; 210/749; 210/753: 210/758: (60) Provisional application No. 61/323,758, filed on Apr. 210/757: 210/723; 210/668; 295.839; 13, 2010, provisional application No. 61/325,996, s filed on Apr. 20, 2010. Publication Classification (57) ABSTRACT (51) Int. Cl. Embodiments are provided for removing a variety of con CO2F I/00 (2006.01) taminants using both rare earth and non-rare earth-containing CO2F I/76 (2006.01) treatment elements. -
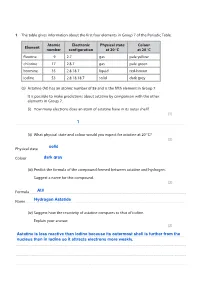
Group 7 Halogens Questions
Save My Exams! – The Home of Revision For more awesome GCSE and A level resources, visit us at www.savemyexams.co.uk/ The table gives information about the first four elements in Group 7 of the Periodic Table. Atomic Electronic Physical state Colour Element number configuration at 20 C at 20 C fluorine 9 2.7 gas pale yellow chlorine 17 2.8.7 gas pale green bromine 35 2.8.18.7 liquid red-brown iodine 53 2.8.18.18.7 solid dark grey (a) Astatine (At) has an atomic number of 85 and is the fifth element in Group 7. It is possible to make predictions about astatine by comparison with the other elements in Group 7. (i) How many electrons does an atom of astatine have in its outer shell? (1) .................................................................................................................................................................................................................................................................................... (ii) What physical state and colour would you expect for astatine at 20 C? (2) Physical state .............................................................................................................................. ................................................................................................................. Colour ................................................................................................................................................................................................................................................................ -
Combined Paper
Cambridge International Examinations Cambridge International Advanced Subsidiary and Advanced Level CHEMISTRY 9701/12 Paper 1 Multiple Choice February/March 2016 1 hour Additional Materials: Multiple Choice Answer Sheet *4624495401 Soft clean eraser Soft pencil (type B or HB is recommended) Data Booklet READ THESE INSTRUCTIONS FIRST Write in soft pencil. Do not use staples, paper clips, glue or correction fluid. * Write your name, Centre number and candidate number on the Answer Sheet in the spaces provided unless this has been done for you. DO NOT WRITE IN ANY BARCODES. There are forty questions on this paper. Answer all questions. For each question there are four possible answers A, B, C and D. Choose the one you consider correct and record your choice in soft pencil on the separate Answer Sheet. Read the instructions on the Answer Sheet very carefully. Each correct answer will score one mark. A mark will not be deducted for a wrong answer. Any rough working should be done in this booklet. Electronic calculators may be used. This document consists of 16 printed pages. IB16 03_9701_12/4RP © UCLES 2016 [Turn over 2 Section A For each question there are four possible answers, A, B, C, and D. Choose the one you consider to be correct. Use of the Data Booklet may be appropriate for some questions. 1 Which compound contains two different elements with identical oxidation states? A HCl O B Mg(OH)2 C Na2SO4 D NH4Cl 2 For the element sulfur, which pair of ionisation energies has the largest difference between them? A third and fourth ionisation energies B fourth and fifth ionisation energies C fifth and sixth ionisation energies D sixth and seventh ionisation energies 3 Which ion has both more electrons than protons and more protons than neutrons? 1 2 16 [H = 1H; D = 1 H; O = 8 O] – + – – A D B H3O C OD D OH 4 Which species contains the smallest number of electrons? A B3+ B Be2+ C H– D He+ © UCLES 2016 9701/12/F/M/16 3 5 Nitric oxide, NO, and bromine vapour react together according to the following equation. -

Prior Knowledge Answers
Prior knowledge Answers Test yourself (page 2) 1 The more reactive metal displaces the less reactive metal from its compound, e.g. Zn(s)CuSO4(aq) → ZnSO4(aq) + Cu(s) 2 A metal or hydrogen 3 Carbon dioxide is produced. acid + carbonate → metal compound (salt) + carbon dioxide + water 4 They are all white crystalline solids. Test yourself (page 6) 5 Oxides of nitrogen split into oxygen and nitrogen on heating. Any ionic salt, such as sodium chloride or aluminium oxide, can be split into elements by electrolysis when molten. 6 Test yourself (page 7) 7 a) H–Cl , HCl b) S=C=S, CS2 8 a) Hydrogen and sulfur, H2S b) Chlorine and oxygen, Cl2O c) Hydrogen and nitrogen, H3N or more usually NH3 © Andrew Hunt, Graham Curtis, Graham Hill 2019 Prior knowledge Answers Test yourself (page 8) 9 a) Copper, steel b) Salt, limestone c) Ice, sugar 10 a) C2H6O2 b) CH3O 11 Because Al(OH)3 contains one Al atom combined with 3 O atoms and 3 H atoms, whereas AlOH3 would contain one Al atom combined with only one O atom and 3 H atoms. 12 a) K2SO4 b) Al2O3 c) PbCO3 b) PbCO3 b) Fe2(SO4)3 Test yourself (page 9) 13 Molecules a) Copper, steel c) Salt, limestone e) Ice, sugar Ions b) copper (i) oxide d) lithium fluoride 14 Test yourself (page 10) 15 a) CH4(g) + 2O2(g) → CO2(g) + 2H2O(g) b) 16 a) H2(g) + Cl2(g) → 2HCl(aq) b) Zn(s) + 2HCl(aq) → ZnCl2(aq) + H2(g) c) 2C2H6(g) + 7O2(g) → 4CO2(g) + 6H2O(l) d) 2Fe(s) + 3Cl2(g) → 2FeCl3(s) Test yourself (page 11) 17 a) Zn(s) + 2HCl(aq)→ ZnCl2(aq) + H2(g) b) CaO(s) + 2HCl(aq) → CaCl2(aq) + H2O(l) c) KOH(aq) + HCl(aq) → KCl(aq) + H2O(l) © Andrew Hunt, Graham Curtis, Graham Hill 2019 Prior knowledge Answers d) ZnCO3(s) + 2HCl(aq) → ZnCl2(aq) + CO2(g) + H2O(l) 18 a) Potassium nitrate b) Calcium chloride c) Copper(ii) sulfate d) Copper(ii) sulfate © Andrew Hunt, Graham Curtis, Graham Hill 2019 1 Atomic structure and the Periodic Table Answers Test yourself (page 13) 1 a) The third and fourth points are still thought to be correct. -

A Review on Non-Relativistic, Fully Numerical Electronic Structure Calculations on Atoms and Diatomic Molecules
A review on non-relativistic, fully numerical electronic structure calculations on atoms and diatomic molecules Susi Lehtola April 23, 2019 Department of Chemistry, University of Helsinki, P.O. Box 55 (A. I. Virtasen aukio 1), FI-00014 University of Helsinki, Finland [email protected].fi Abstract The need for accurate calculations on atoms and diatomic molecules is motivated by the opportunities and challenges of such studies. The most commonly-used ap- proach for all-electron electronic structure calculations in general – the linear combina- tion of atomic orbitals (LCAO) method – is discussed in combination with Gaussian, Slater a.k.a. exponential, and numerical radial functions. Even though LCAO calcu- lations have major benefits, their shortcomings motivate the need for fully numerical approaches based on, e.g. finite differences, finite elements, or the discrete variable representation, which are also briefly introduced. Applications of fully numerical approaches for general molecules are briefly reviewed, and their challenges are discussed. It is pointed out that the high level of symmetry present in atoms and diatomic molecules can be exploited to fashion more efficient fully numerical approaches for these special cases, after which it is possible to routinely per- form all-electron Hartree–Fock and density functional calculations directly at the basis set limit on such systems. Applications of fully numerical approaches to calculations on atoms as well as diatomic molecules are reviewed. Finally, a summary and outlook is given.