Spatial-Temporal Characteristics and the Epidemiology of Haemorrhagic Fever with Renal Syndrome from 2007 to 2016 in Zhejiang Pr
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Risk Factors for Carbapenem-Resistant Pseudomonas Aeruginosa, Zhejiang Province, China
Article DOI: https://doi.org/10.3201/eid2510.181699 Risk Factors for Carbapenem-Resistant Pseudomonas aeruginosa, Zhejiang Province, China Appendix Appendix Table. Surveillance for carbapenem-resistant Pseudomonas aeruginosa in hospitals, Zhejiang Province, China, 2015– 2017* Years Hospitals by city Level† Strain identification method‡ excluded§ Hangzhou First 17 People's Liberation Army Hospital 3A VITEK 2 Compact Hangzhou Red Cross Hospital 3A VITEK 2 Compact Hangzhou First People’s Hospital 3A MALDI-TOF MS Hangzhou Children's Hospital 3A VITEK 2 Compact Hangzhou Hospital of Chinese Traditional Hospital 3A Phoenix 100, VITEK 2 Compact Hangzhou Cancer Hospital 3A VITEK 2 Compact Xixi Hospital of Hangzhou 3A VITEK 2 Compact Sir Run Run Shaw Hospital, School of Medicine, Zhejiang University 3A MALDI-TOF MS The Children's Hospital of Zhejiang University School of Medicine 3A MALDI-TOF MS Women's Hospital, School of Medicine, Zhejiang University 3A VITEK 2 Compact The First Affiliated Hospital of Medical School of Zhejiang University 3A MALDI-TOF MS The Second Affiliated Hospital of Zhejiang University School of 3A MALDI-TOF MS Medicine Hangzhou Second People’s Hospital 3A MALDI-TOF MS Zhejiang People's Armed Police Corps Hospital, Hangzhou 3A Phoenix 100 Xinhua Hospital of Zhejiang Province 3A VITEK 2 Compact Zhejiang Provincial People's Hospital 3A MALDI-TOF MS Zhejiang Provincial Hospital of Traditional Chinese Medicine 3A MALDI-TOF MS Tongde Hospital of Zhejiang Province 3A VITEK 2 Compact Zhejiang Hospital 3A MALDI-TOF MS Zhejiang Cancer -

2.21 Zhejiang Province Zhejiang Donglian Group Co., Ltd.,1 Affiliated
2.21 Zhejiang Province Zhejiang Donglian Group Co., Ltd.,1 affiliated to Zhejiang Provincial Prison Administration Bureau, has 17 prison enterprises Legal representative of the prison company: Hu Fangrui, Chairman of Zhejiang Donglian Group Co., Ltd His official positions in the prison system: Director of Zhejiang Provincial Prison Administration Bureau2 No. Company Name of the Legal Person Legal Registered Business Scope Company Notes on the Prison Name Prison, to and representative/Title Capital Address which the Shareholder(s) Company Belongs 1 Zhejiang Zhejiang Zhejiang Hu Fangrui 11.95 million Capital management; industrial 15th – 17th Zhejiang Provincial Prison Administration Donglian Group Provincial Provincial Chairman of Zhejiang yuan investment and development; Floors, No. Bureau is a deputy department-level Co., Ltd. Prison Government Donglian Group Co., production, processing and sale 276 Jianguo administrative agency, which is in charge of Administration Ltd; Director of of electromechanical equipment, North Road, implementing penalties and running prison Bureau Zhejiang Provincial hardware and electrical Hangzhou City enterprises. It is under the jurisdiction of Prison Administration equipment, chemical raw the Provincial Department of Justice. Bureau3 materials and products Address: 110 Tianmushan Road, Hangzhou (excluding dangerous goods and City. precursor chemicals), metallic The bureau assigns responsibilities of materials, decorative building production, operation and management to materials, daily necessities and -

Domestic and International Challenges for the Textile Industry in Shaoxing (Zhejiang)
Special feature China perspectives Domestic and International Challenges for the Textile Industry in Shaoxing (Zhejiang) SHI LU ABSTRACT: This article recounts the transformations that have taken place in the textile industry in Shaoxing, Zhejiang Province, over the course of the past 30 years. It reveals the importance of the local setup and the links that have built up between companies, mar - kets, and the state and its departments. It also exposes the difficulties experienced by companies as they try to adapt to their changing environment, whether in terms of opportunities offered by the domestic or international markets, or new regulations. KEYWORDS: textile industry, clusters, developmental state, governance, market. Introduction markets increased, the cost of labour rose, and new environmental require - ments were imposed. This contribution looks back over the transformations he developmental state concept was developed by Chalmers Johnson and the ways in which companies have adapted to these changes in the in the early 1980s to describe the role of the state in the economic case of the textile industry in Zhejiang Province and, more particularly, in successes enjoyed by Japan, which he considered to have been un - the city of Shaoxing. T (1) derestimated. It was subsequently used to refer to the ability of economic In 2013, 15% of companies in Zhejiang Province were operating in the bureaucracies to guide development in South Korea and Taiwan, channelling textile and clothing industries, making it one of China’s main centres for private investment towards growth sectors and allowing these economies manufacturing textile products at that time. (4) The city of Shaoxing, a for - to benefit from a comparative advantage in international competition. -

The Superfamily Calopterygoidea in South China: Taxonomy and Distribution. Progress Report for 2009 Surveys Zhang Haomiao* *PH D
International Dragonfly Fund - Report 26 (2010): 1-36 1 The Superfamily Calopterygoidea in South China: taxonomy and distribution. Progress Report for 2009 surveys Zhang Haomiao* *PH D student at the Department of Entomology, College of Natural Resources and Environment, South China Agricultural University, Guangzhou 510642, China. Email: [email protected] Introduction Three families in the superfamily Calopterygoidea occur in China, viz. the Calo- pterygidae, Chlorocyphidae and Euphaeidae. They include numerous species that are distributed widely across South China, mainly in streams and upland running waters at moderate altitudes. To date, our knowledge of Chinese spe- cies has remained inadequate: the taxonomy of some genera is unresolved and no attempt has been made to map the distribution of the various species and genera. This project is therefore aimed at providing taxonomic (including on larval morphology), biological, and distributional information on the super- family in South China. In 2009, two series of surveys were conducted to Southwest China-Guizhou and Yunnan Provinces. The two provinces are characterized by karst limestone arranged in steep hills and intermontane basins. The climate is warm and the weather is frequently cloudy and rainy all year. This area is usually regarded as one of biodiversity “hotspot” in China (Xu & Wilkes, 2004). Many interesting species are recorded, the checklist and photos of these sur- veys are reported here. And the progress of the research on the superfamily Calopterygoidea is appended. Methods Odonata were recorded by the specimens collected and identified from pho- tographs. The working team includes only four people, the surveys to South- west China were completed by the author and the photographer, Mr. -

Tonatory Patterns in Taizhou Wu Tones
TONATORY PATTERNS IN TAIZHOU WU TONES Phil Rose Emeritus Faculty, Australian National University [email protected] ABSTRACT 台州 subgroup of Wu to which Huángyán belongs. The issue has significance within descriptive Recordings of speakers of the Táizhou subgroup of tonetics, tonatory typology and historical linguistics. Wu Chinese are used to acoustically document an Wu dialects – at least the conservative varieties – interaction between tone and phonation first attested show a wide range of tonatory behaviour [11]. One in 1928. One or two of their typically seven or eight finds breathy or ventricular phonation in groups of tones are shown to have what sounds like a mid- tones characterising natural tonal classes of Rhyme glottal-stop, thus demonstrating a new importance for phonotactics and Wu’s complex tone pattern in Wu tonatory typology. Possibly reflecting sandhi. One also finds a single tone characterised by gradual loss, larygealisation appears restricted to the a different non-modal phonation type [12]; or even north and north-west, and is absent in Huángyán two different non-modal phonation types in two dialect where it was first described. A perturbatory tones. However, the Huangyan-type tonation seems model of the larygealisation is tested in an to involve a new variation, with the same phonation experiment determining how much of the complete type in two different tones from the same historical tonal F0 contour can be restored from a few tonal category, thus prompting speculation that it centiseconds of modal F0 at Rhyme onset and offset. developed before the tonal split. The results are used both to acoustically quantify laryngealised tonal F0, with its problematic jitter and 2. -
Review of Dicrotendipes Kieffer from China (Diptera, Chironomidae)
A peer-reviewed open-access journal ZooKeys 183: 23–36Review (2012) of Dicrotendipes Kieffer from China (Diptera, Chironomidae) 23 doi: 10.3897/zookeys.183.2834 RESEARCH ARTICLE www.zookeys.org Launched to accelerate biodiversity research Review of Dicrotendipes Kieffer from China (Diptera, Chironomidae) Xin Qi1,†, Xiao-Long Lin2,‡, Xin-Hua Wang2,§ 1 College of Life Science, Taizhou University, Linhai, Zhejiang 317000, China 2 College of Life Science, Nankai University, Tianjin 300071, China † urn:lsid:zoobank.org:author:C902B210-CE50-4C13-885B-CE172F2F633B ‡ urn:lsid:zoobank.org:author:AC3964DC-0709-4DCB-96AA-6EBEDFA04C07 § urn:lsid:zoobank.org:author:37612E15-93C0-4263-80F7-5322036240F9 Corresponding author: Xin-Hua Wang ([email protected]) Academic editor: V. Blagoderov | Received 5 February 2012 | Accepted 11 April 2012 | Published 19 April 2012 urn:lsid:zoobank.org:pub:6150473B-3A02-4926-BFD1-201002F7A198 Citation: Qi X, Lin XL, Wang XH (2012) Review of Dicrotendipes Kieffer from China (Diptera, Chironomidae). ZooKeys 183: 23–36. doi: 10.3897/zookeys.183.2834 Abstract The genus Dicrotendipes Kieffer from China, including 8 species, is reviewed. Two new species, D. nudus sp. n. and D. saetanumerosus sp. n. are described and the male imagines are illustrated; the record of D. fusconotatus (Kieffer) is the first for China. A key to the males of Dicrotendipes in China is given. Keywords Chironomidae, Dicrotendipes, new species, key, China Introduction The genusDicrotendipes was erected by Kieffer in 1913, with Dicrotendipes septem- maculatus (Becker, 1908) as type species. Adults of Dicrotendipes have been considered as pests due to large emergences (Frommer and Rauch 1971; Epler 1988), and have been implicated in allergic reactions in humans in Africa (Cranston et al. -

Request for Recruitment Program of Foreign Experts Zheijang Final
EDUCATION & RESEARCH Request for Recruitment Program of Foreign Experts 1 Client : Zhejiang Normal University Industry : Higher Education Region : Jinhua, Zhejiang Province Zhejiang Normal University(ZNU) is one of the key universities of Zhejiang Province. ZNU emphasizes in teacher education with multiple branches of learning. The University consists of 19 colleges offering 61 undergraduate programs. It has an enrolment over Client Information (main 25,700 undergraduates, 5,000 postgraduates, and 15,000 adult students in various adult areas of activity, etc. ): education programs. The total staff is about 2,700. In 2009, ZNU became a doctoral degree project construction unit. Now there are 23 senior subject master degree programs and 11 professional degree Master programs. There are complete infrastructure, rich library resources, and advanced equipment in ZNU. 1. Leverage the key discipline platform of pure and applied mathematics to strengthen international and mainland academic exchange. Invite internationally well-known scholars to visit, give seminars or short courses to introduce research results and directions in Nature of Activity frontiers of mathematics. Elevate discipline’s international recognition and influence. Requirement for 2. Carefully select research topics. Choose topics with theoretical depth or those with Experts (main task, goal prospect of wide application and in the mainstream of mathematics with research content keeping with international frontiers. Initiate and develop new research direction. to be attained, etc. ): 3. Train high quality researchers. Strengthen the training of graduate students and young faculty members; improve their creativity and implementation skills. Thru short courses to systematically introduce the current state of research, research topics and research methods. Broaden the horizon and area of our research team. -

Oktober 2019 Land Name Adresse Warengruppe Mitarbeiteranzahl
Produktionsstätten nach Land Letzte Aktualisierung: Oktober 2019 Land Name Adresse Warengruppe Mitarbeiteranzahl Ägypten Arab Novelties Weaving Terry Co. El Rahbeen Industrial Zone-Front Of Moubark Cool, El-Mahalla El-Kubra, Al Gharbiyah Heimtextilien 0-500 Mac Carpet 10th Ramadad City, Zone B1B3, 1o th of Ramadan Heimtextilien 3001-4000 Oriental Weavers 10th of Ramadan City, Industrial A1, Industrial 1 El Sharkeya, Kairo Heimtextilien >5000 The Egyptian Company for Trade Industry Canal Suez St. Moharam Bey, Manshia Guededah, 00203 Alexandria Bekleidungstextilien 0-500 Bangladesch ABM Fashions Ltd. Kashimpur Road, Holding No. 1143-1145, Konabari, 1751 Gazipur Bekleidungstextilien 3001-4000 AKH Stitch Art Ltd. Chandanpur, Rajfulbaria,Hemayetpur, Savar, 1340 Dhaka Bekleidungstextilien 2001-3000 Ananta Jeanswear Ltd. Kabi Jashim Uddin Road No. 134/123, Pagar, Tongi, 1710 Gazipur Bekleidungstextilien 3001-4000 Aspire Garments Ltd. 491, Dhalla Bazar, Singair,1820 Manikganj Bekleidungstextilien 2001-3000 BHIS Apparels Ltd. Dattapara No. 671, 0-5 Floor, Tongi, Hossain Market, 1712 Gazipur/Dhaka Bekleidungstextilien 2001-3000 Blue Planet Knitwear Ltd. P.O: Tengra, Sreepur, Sreepur, Gazipur District 1740, Dhaka Bekleidungstextilien 1001-2000 Chaity Composite Ltd. Chotto Silmondi, Tirpurdi, Sonargaon, Narayangonj, 1440 Dhaka Bekleidungstextilien 4001-5000 Chorka Textile Ltd. Kazirchor, Danga, Polas, Narshingdi,1720 Narshingdi-Dhaka Bekleidungstextilien 4001-5000 Citadel Apparels Ltd. Joy Bangla Road, Kunia, K.B. Bazar, Gazipur Sadar, Gazipur 1704 Dhaka Bekleidungstextilien 501-1000 Cotton Dyeing & Finishing Mills Ltd. Amtoli Union No. 10, Habirbari, P. O-Seedstore Bazar, P.S.-Valuka, Mymensingh-2240, Bekleidungstextilien 1001-2000 Mymensingh, 2240 Dhaka Crossline Factory (Pvt) Ltd. Vadam 25, Uttarpara, Nishatnagar, Tongi, Gazipur, 1711 Dhaka Bekleidungstextilien 1001-2000 Crossline Knit Fabrics Ltd. -

Shop Direct Factory List Dec 18
Factory Factory Address Country Sector FTE No. workers % Male % Female ESSENTIAL CLOTHING LTD Akulichala, Sakashhor, Maddha Para, Kaliakor, Gazipur, Bangladesh BANGLADESH Garments 669 55% 45% NANTONG AIKE GARMENTS COMPANY LTD Group 14, Huanchi Village, Jiangan Town, Rugao City, Jaingsu Province, China CHINA Garments 159 22% 78% DEEKAY KNITWEARS LTD SF No. 229, Karaipudhur, Arulpuram, Palladam Road, Tirupur, 641605, Tamil Nadu, India INDIA Garments 129 57% 43% HD4U No. 8, Yijiang Road, Lianhang Economic Development Zone, Haining CHINA Home Textiles 98 45% 55% AIRSPRUNG BEDS LTD Canal Road, Canal Road Industrial Estate, Trowbridge, Wiltshire, BA14 8RQ, United Kingdom UK Furniture 398 83% 17% ASIAN LEATHERS LIMITED Asian House, E. M. Bypass, Kasba, Kolkata, 700017, India INDIA Accessories 978 77% 23% AMAN KNITTINGS LIMITED Nazimnagar, Hemayetpur, Savar, Dhaka, Bangladesh BANGLADESH Garments 1708 60% 30% V K FASHION LTD formerly STYLEWISE LTD Unit 5, 99 Bridge Road, Leicester, LE5 3LD, United Kingdom UK Garments 51 43% 57% AMAN GRAPHIC & DESIGN LTD. Najim Nagar, Hemayetpur, Savar, Dhaka, Bangladesh BANGLADESH Garments 3260 40% 60% WENZHOU SUNRISE INDUSTRIAL CO., LTD. Floor 2, 1 Building Qiangqiang Group, Shanghui Industrial Zone, Louqiao Street, Ouhai, Wenzhou, Zhejiang Province, China CHINA Accessories 716 58% 42% AMAZING EXPORTS CORPORATION - UNIT I Sf No. 105, Valayankadu, P. Vadugapal Ayam Post, Dharapuram Road, Palladam, 541664, India INDIA Garments 490 53% 47% ANDRA JEWELS LTD 7 Clive Avenue, Hastings, East Sussex, TN35 5LD, United Kingdom UK Accessories 68 CAVENDISH UPHOLSTERY LIMITED Mayfield Mill, Briercliffe Road, Chorley Lancashire PR6 0DA, United Kingdom UK Furniture 33 66% 34% FUZHOU BEST ART & CRAFTS CO., LTD No. 3 Building, Lifu Plastic, Nanshanyang Industrial Zone, Baisha Town, Minhou, Fuzhou, China CHINA Homewares 44 41% 59% HUAHONG HOLDING GROUP No. -

Table of Codes for Each Court of Each Level
Table of Codes for Each Court of Each Level Corresponding Type Chinese Court Region Court Name Administrative Name Code Code Area Supreme People’s Court 最高人民法院 最高法 Higher People's Court of 北京市高级人民 Beijing 京 110000 1 Beijing Municipality 法院 Municipality No. 1 Intermediate People's 北京市第一中级 京 01 2 Court of Beijing Municipality 人民法院 Shijingshan Shijingshan District People’s 北京市石景山区 京 0107 110107 District of Beijing 1 Court of Beijing Municipality 人民法院 Municipality Haidian District of Haidian District People’s 北京市海淀区人 京 0108 110108 Beijing 1 Court of Beijing Municipality 民法院 Municipality Mentougou Mentougou District People’s 北京市门头沟区 京 0109 110109 District of Beijing 1 Court of Beijing Municipality 人民法院 Municipality Changping Changping District People’s 北京市昌平区人 京 0114 110114 District of Beijing 1 Court of Beijing Municipality 民法院 Municipality Yanqing County People’s 延庆县人民法院 京 0229 110229 Yanqing County 1 Court No. 2 Intermediate People's 北京市第二中级 京 02 2 Court of Beijing Municipality 人民法院 Dongcheng Dongcheng District People’s 北京市东城区人 京 0101 110101 District of Beijing 1 Court of Beijing Municipality 民法院 Municipality Xicheng District Xicheng District People’s 北京市西城区人 京 0102 110102 of Beijing 1 Court of Beijing Municipality 民法院 Municipality Fengtai District of Fengtai District People’s 北京市丰台区人 京 0106 110106 Beijing 1 Court of Beijing Municipality 民法院 Municipality 1 Fangshan District Fangshan District People’s 北京市房山区人 京 0111 110111 of Beijing 1 Court of Beijing Municipality 民法院 Municipality Daxing District of Daxing District People’s 北京市大兴区人 京 0115 -

Rhinogobius Immaculatus, a New Species of Freshwater Goby (Teleostei: Gobiidae) from the Qiantang River, China
ZOOLOGICAL RESEARCH Rhinogobius immaculatus, a new species of freshwater goby (Teleostei: Gobiidae) from the Qiantang River, China Fan Li1,2,*, Shan Li3, Jia-Kuan Chen1 1 Institute of Biodiversity Science, Ministry of Education Key Laboratory for Biodiversity Science and Ecological Engineering, Fudan University, Shanghai 200433, China 2 Shanghai Ocean University, Shanghai 200090, China 3 Shanghai Natural History Museum, Branch of Shanghai Science & Technology Museum, Shanghai 200041, China ABSTRACT non-diadromous (landlocked) (Chen et al., 1999a, 2002; Chen A new freshwater goby, Rhinogobius immaculatus sp. & Kottelat, 2005; Chen & Miller, 2014; Huang & Chen, 2007; Li & Zhong, 2009). nov., is described here from the Qiantang River in In total, 44 species of Rhinogobius have been recorded in China. It is distinguished from all congeners by the China (Chen et al., 2008; Chen & Miller, 2014; Huang et al., following combination of characters: second dorsal-fin 2016; Huang & Chen, 2007; Li et al., 2007; Li & Zhong, 2007, rays I, 7–9; anal-fin rays I, 6–8; pectoral-fin rays 2009; Wu & Zhong, 2008; Yang et al., 2008), eight of which 14–15; longitudinal scales 29–31; transverse scales have been reported from the Qiantang River basin originating 7–9; predorsal scales 2–5; vertebrae 27 (rarely 28); in southeastern Anhui Province to eastern Zhejiang Province. These species include R. aporus (Zhong & Wu, 1998), R. davidi preopercular canal absent or with two pores; a red (Sauvage & de Thiersant, 1874), R. cliffordpopei (Nichols, oblique stripe below eye in males; branchiostegal 1925), R. leavelli (Herre, 1935a), R. lentiginis (Wu & Zheng, membrane mostly reddish-orange, with 3–6 irregular 1985), R. -
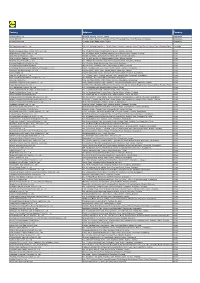
Factory Address Country
Factory Address Country Durable Plastic Ltd. Mulgaon, Kaligonj, Gazipur, Dhaka Bangladesh Lhotse (BD) Ltd. Plot No. 60&61, Sector -3, Karnaphuli Export Processing Zone, North Potenga, Chittagong Bangladesh Bengal Plastics Ltd. Yearpur, Zirabo Bazar, Savar, Dhaka Bangladesh ASF Sporting Goods Co., Ltd. Km 38.5, National Road No. 3, Thlork Village, Chonrok Commune, Korng Pisey District, Konrrg Pisey, Kampong Speu Cambodia Ningbo Zhongyuan Alljoy Fishing Tackle Co., Ltd. No. 416 Binhai Road, Hangzhou Bay New Zone, Ningbo, Zhejiang China Ningbo Energy Power Tools Co., Ltd. No. 50 Dongbei Road, Dongqiao Industrial Zone, Haishu District, Ningbo, Zhejiang China Junhe Pumps Holding Co., Ltd. Wanzhong Villiage, Jishigang Town, Haishu District, Ningbo, Zhejiang China Skybest Electric Appliance (Suzhou) Co., Ltd. No. 18 Hua Hong Street, Suzhou Industrial Park, Suzhou, Jiangsu China Zhejiang Safun Industrial Co., Ltd. No. 7 Mingyuannan Road, Economic Development Zone, Yongkang, Zhejiang China Zhejiang Dingxin Arts&Crafts Co., Ltd. No. 21 Linxian Road, Baishuiyang Town, Linhai, Zhejiang China Zhejiang Natural Outdoor Goods Inc. Xiacao Village, Pingqiao Town, Tiantai County, Taizhou, Zhejiang China Guangdong Xinbao Electrical Appliances Holdings Co., Ltd. South Zhenghe Road, Leliu Town, Shunde District, Foshan, Guangdong China Yangzhou Juli Sports Articles Co., Ltd. Fudong Village, Xiaoji Town, Jiangdu District, Yangzhou, Jiangsu China Eyarn Lighting Ltd. Yaying Gang, Shixi Village, Shishan Town, Nanhai District, Foshan, Guangdong China Lipan Gift & Lighting Co., Ltd. No. 2 Guliao Road 3, Science Industrial Zone, Tangxia Town, Dongguan, Guangdong China Zhan Jiang Kang Nian Rubber Product Co., Ltd. No. 85 Middle Shen Chuan Road, Zhanjiang, Guangdong China Ansen Electronics Co. Ning Tau Administrative District, Qiao Tau Zhen, Dongguan, Guangdong China Changshu Tongrun Auto Accessory Co., Ltd.