DOCSLIB.ORG

A New Approach in Assignment Problem

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A New Approach in Assignment Problem International Journal of Pure and Applied Mathematics Volume 113 No. 13 2017, 122 { 131 ISSN: 1311-8080 (printed version); ISSN: 1314-3395 (on-line version) url: http://www.ijpam.eu Special Issue ijpam.eu A NEW APPROACH IN ASSIGNMENT PROBLEM P. Sumathi1, V. Preethy2 1Department of Mathematics, Bharath University Chennai - 600 073, Tamilnadu, India psumathi16@rediffmail.com 2Department of Mathematics, Bharath University Chennai - 600 073, Tamilnadu, India [email protected] Abstract This paper discusses the Kaprekar constant and Kaprekar numbers in number theory. A brief account of kaprekar procedure and its number of convergence of different digits of number is also being explained. An interesting innovation of connecting Kaprekar procedure and Kaprekar constant with assignment problem to find the optimum solution and the corresponding number of iterations to the respective numbers will be converged is also being portrayed. AMS Subject Classification: 11E76, 11E81, 90C08. Key Words and Phrases: Kaprekar Number, Kaprekar Constant, Kaprekar Procedure, Assignment problem. 1 Introduction Number theory is an ancient subject but we still cannot answer the integers in Number theory. It has extensive applications in recent 30 years. There are different types of numbers which add beauty to number theory. One among such fascinating numbers is Kaprekar numbers whose brief account has been portrayed. ijpam.eu 122 2017 International Journal of Pure and Applied Mathematics Special Issue This paper deals about the Kaprekar number and Kaprekar constant .and a new innovative method is proposed using Kaprekar procedure in assignment problem. In this paper Section 2 deals with the concept of Kaprekar Numbers with examples. Section 3 and Section 4 portrays the Algebraic expression of Kaprekar Numbers and the Procedure for splitting the Kaprekar Numbers in two cases. A brief account on Kaprekar Constant and Kaprekar Procedure is dealt in Section 5 and Section 6. In Section 7, an innovative approach of combining Kaprekar Procedure with Assignment problem is clearly discussed. 2 Kaprekar Numbers A Kaprekar number for a given base is a non-negative integer, the representation of whose square in that base can be split up into two parts such that add up to the original number again. In other words, a Kaprekar number n is such that n2 can be split into two so that the two parts sum to n. Example 1. 452 =2025 20+25=45 7032 =494209 494+209=703 3 Algebraic Expression of Kaprekar Number Let n be a k-digit integer in base b. Then n is said to be a Kaprekar number in base b, if n2 has the property such that when we add the number formed by its right hand digits to that formed by its left hand digits, we get n. In algebraic form, an integer n such that in a given base b has k 1 − 2 i n = dib i=0 X where, K - number of digits in square of the given number. ijpam.eu 123 2017 International Journal of Pure and Applied Mathematics Special Issue di - digits with d0 the least significant digit and dk 1 the most − significant digit. Example 2. Consider the number n = 297, n2 = 88209. Apply the formula, k 1 − 2 i n = dib i=0 X Here, k =5,d0 =9,d1 =0,d2 =2,d3 =8,d4 =8,b = 10 Hence, k 1 − 2 i 297 = dib i=0 X0 1 2 0 1 = d0b + d1b + d2b + d3b + d4b =9 100 +0 102 +2 102 +8 103 +8 104 × × × × × = 9+0+200+8000+80000 2972 = 88209 4 Procedure for Splitting of Square of a Kaprekar Number Consider a Kaprekar number. Let it be denoted as n. Find the square of n. Let it be n2. Let the number of digits in n2 be k. Now, here arises two cases, Case (1): If k is odd, then [k/2] k 1 − i i [k/2] 1 n = dib + dib − − i=0 X i=[Xk/2]+1 Case (ii): If k is even, then k 2 1 k 1 − − i i k n = dib + dib − 2 i=0 i= k X X2 ijpam.eu 124 2017 International Journal of Pure and Applied Mathematics Special Issue 5 Kaprekar Constant A number that remain unchanged on applying the Kaprekar process on it is known as Kaprekar constant. 5.1 Kaprekar constant for various digit numbers The Kaprekar constant for Three digit numbers is 495 Four digit numbers is 6174 Six digit numbers is 549945, 631764 Eight digit number is 63317664, 97508421 Nine digit number is 554999445, 864197532 Ten digit number is 6333176664, 9753086421 6 Kaprekar Process Procedure for three digit numbers to reach the Kaprekar constant Choose any three digit number consisting of three distinct digits. Rearrange the digits into descending order and then into ascending order including leading zeroes. Find the difference of these digits. It may be 495. If not, repeat the same procedure to the answer obtained from the differences of those digits. The end result will terminate to a number 495 which is the Kaprekar Constant for three digit numbers. The Procedure is similar for different digits of numbers. 7 Coupling Kaprekar Procedure with Assignment Problem This concept provokes an interesting gateway of getting solution of number of iterations of four digit numbers to reach the Kaprekar constant in assignment problem procedure. ijpam.eu 125 2017 International Journal of Pure and Applied Mathematics Special Issue Algorithm: Step 1: Consider any four digit numbers at least two of its number is distinct. Step 2: The number of iterations for those numbers to reach the Kaprekar constant 6174 should be calculated initially using simple method. Step 3: The numbers are arranged in 4 4 matrix by placing × any two of the numbers in ascending order and the remaining two numbers in descending order. Step 4: The actual numbers are taken along the column wise and the corresponding iterations are taken along row wise outside the matrix. Step 5: Now by applying the procedure of the assignment problem, the optimum solution is obtained and the corresponding number of iterations to the respective numbers will be converged. Example 3. Consider the following numbers with their corresponding number of iterations 1467-1, 3087-2, 1432-3, 5238-4 Step 1: Step 2: Row Minima Step 3: Column Minima ijpam.eu 126 2017 International Journal of Pure and Applied Mathematics Special Issue Number of lines = Order of matrix, Hence the optimality is not obtained. 6 Add 1 to the numbers in the lines of intersection and sub 1 to the numbers not on the line. Step 4: Number of lines = Order of matrix Hence the optimality is obtained. Step 5: Finally the numbers are converged to their respective number of iterations. 1467 1 3087 → 2 → 1432 3 5238 → 4 → ijpam.eu 127 2017 International Journal of Pure and Applied Mathematics Special Issue 8 Conclusion In this paper Kaprekar Constant and Kaprekar Numbers were discussed in detailed with some examples. An interesting new innovative method of connecting Kaprekar procedure and Kaprekar constant with assignment problem was proposed. Using assignment problem the optimum solution is obtained and the corresponding number of iterations to the respective numbers will be converged. References [1] D.R. Kaprekar, An interesting property of the number 6174 scriptamathematica, 15 (1955), 244-245. [2] D.RKaprekar, On Kaprekar Numbers, Journal of Recreational Math, 13, No. 2 (1980), 81-82. [3] D. Lannucci, TheKaprekar Numbers, Journal of Integer Sequence, 3 (2000). [4] P.K. Srinivasan, The wonder world of Kaprekar Numbers, First edition AMTI (2004). [5] S. Paulraj, P. Sumathi, A comparative study of redundant constraints identification methods in linear programming problems, Mathematical Problems in Engineering, 2010, Article ID 723402, (2010), 16 pages. [6] K. Kadhirvel, K. Balamurugan, Method For Solving Hungar- ian Assignment Problems Using Triangular And Trapezoidal Fuzzy Number, International Journal of Engineering, 2, No. 5 (2012), 399-403. [7] Shweta Singh, G.C. Dubey, Rajesh Shrivastava, A Com- parative Analysis of Assignment Problem, IOSR Journal of Engineering (IOSRJEN), 2, No. 8 (2012), 1-15. [8] S. Paulraj, P. Sumathi, A new approach for selecting a constraint in linear programming problems to identify the redundant Constraints, International Journal of Scientific and Engineering Research, 3, No. 3 (2012). ijpam.eu 128 2017 International Journal of Pure and Applied Mathematics Special Issue [9] P. Sumathi, S. Paulraj, Identification of redundant constraints in large s cale linear programming problems with minimal computational effort, Applied Mathematical Sciences, 7, No. 80 (2013), 3963-3974. [10] Kanjana Thongsanit, Solving the Course Classroom Assign- ment Problem for a University, Silpakorn U & Tech J, 8, No. 1 (2014), 46-52. [11] A. Karpagam, P. Sumathi, Innovative Method for Solv- ing Fuzzy Linear Programming Problems with Symmetric Trapezoidal Fuzzy Numbers, International Journal of Latest Research in Science and Technology, 3, No. 6 (2014), 95-98. [12] A. Karpagam, P. Sumathi, New Approach to Solve Fuzzy Linear Programming Problems by the Ranking Function, Bonfring International Journal of Data Mining, 4, No. 4 (2014), 22-25. [13] P. Sumathi, A. Gangadharan, Selection of constraints with a new approach in linear programming problems, Applied Mathematical Sciences, 8, No. 27 (2014), 1311-1321. [14] P. Sumathi, A. Gangadhara, New technique to detect redundant constraints in large scale linear programming problems, International Journal of Scientific Research, 3, No. 6 (2014), 236-238. [15] P. Sumathi, A New Tactic for Finding Irrelevant Constraints in Linear Programming Problems, International Journal of Scientific and Engineering Research, 6, No. 3 (2015), 66-69. [16] Duˇsan Teichmann, Michal Dorda, KarelGolc, Helena Bnova, Locom otive assignment problem with heterogeneous vehicle fleet and hiringexternal locomotives, Mathematical Problems in Engineering (2015), Article ID 583909, 7 pages. [17] K. Yuvarekha, V. Nandakumar, Dr.
Load more

Recommended publications
  • Monthly Science and Maths Magazine 01
    1 GYAN BHARATI SCHOOL QUEST….. Monthly Science and Mathematics magazine Edition: DECEMBER,2019 COMPILED BY DR. KIRAN VARSHA AND MR. SUDHIR SAXENA 2 IDENTIFY THE SCIENTIST She was an English chemist and X-ray crystallographer who made contributions to the understanding of the molecular structures of DNA , RNA, viruses, coal, and graphite. She was never nominated for a Nobel Prize. Her work was a crucial part in the discovery of DNA, for which Francis Crick, James Watson, and Maurice Wilkins were awarded a Nobel Prize in 1962. She died in 1958, and during her lifetime the DNA structure was not considered as fully proven. It took Wilkins and his colleagues about seven years to collect enough data to prove and refine the proposed DNA structure. RIDDLE TIME You measure my life in hours and I serve you by expiring. I’m quick when I’m thin and slow when I’m fat. The wind is my enemy. Hard riddles want to trip you up, and this one works by hitting you with details from every angle. The big hint comes at the end with the wind. What does wind threaten most? I have cities, but no houses. I have mountains, but no trees. I have water, but no fish. What am I? This riddle aims to confuse you and get you to focus on the things that are missing: the houses, trees, and fish. 3 WHY ARE AEROPLANES USUALLY WHITE? The Aeroplanes might be having different logos and decorations. But the colour of the aeroplane is usually white.Painting the aeroplane white is most practical and economical.
    [Show full text]
  • Eureka Issue 61
    Eureka 61 A Journal of The Archimedeans Cambridge University Mathematical Society Editors: Philipp Legner and Anja Komatar © The Archimedeans (see page 94 for details) Do not copy or reprint any parts without permission. October 2011 Editorial Eureka Reinvented… efore reading any part of this issue of Eureka, you will have noticed The Team two big changes we have made: Eureka is now published in full col- our, and printed on a larger paper size than usual. We felt that, with Philipp Legner Design and Bthe internet being an increasingly large resource for mathematical articles of Illustrations all kinds, it was necessary to offer something new and exciting to keep Eu- reka as successful as it has been in the past. We moved away from the classic Anja Komatar Submissions LATEX-look, which is so common in the scientific community, to a modern, more engaging, and more entertaining design, while being conscious not to Sean Moss lose any of the mathematical clarity and rigour. Corporate Ben Millwood To make full use of the new design possibilities, many of this issue’s articles Publicity are based around mathematical images: from fractal modelling in financial Lu Zou markets (page 14) to computer rendered pictures (page 38) and mathemati- Subscriptions cal origami (page 20). The Showroom (page 46) uncovers the fundamental role pictures have in mathematics, including patterns, graphs, functions and fractals. This issue includes a wide variety of mathematical articles, problems and puzzles, diagrams, movie and book reviews. Some are more entertaining, such as Bayesian Bets (page 10), some are more technical, such as Impossible Integrals (page 80), or more philosophical, such as How to teach Physics to Mathematicians (page 42).
    [Show full text]
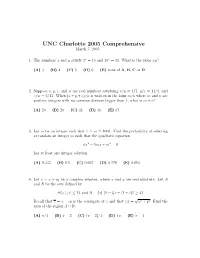
  • The 2005 Exam, Problems Only
    UNC Charlotte 2005 Comprehensive March 7, 2005 1. The numbers x and y satisfy 2x = 15 and 15y = 32. What is the value xy? (A) 3 (B) 4 (C) 5 (D) 6 (E) none of A, B, C or D 2. Suppose x, y, z, and w are real numbers satisfying x/y = 4/7, y/z = 14/3, and z/w = 3/11. When (x + y + z)/w is written in the form m/n where m and n are positive integers with no common divisors bigger than 1, what is m + n? (A) 20 (B) 26 (C) 32 (D) 36 (E) 37 3. Let m be an integer such that 1 ≤ m ≤ 1000. Find the probability of selecting at random an integer m such that the quadratic equation 6x2 − 5mx + m2 = 0 has at least one integer solution. (A) 0.333 (B) 0.5 (C) 0.667 (D) 0.778 (E) 0.883 4. Let z = x + iy be a complex number, where x and y are real numbers. Let A and B be the sets defined by A{z | |z| ≤ 2} and B = {z| (1 − i)z + (1 + i)¯z ≥ 4}. √ Recall that z = x − iy is the conjugate of z and that |z| = x2 + y2. Find the area of the region A ∩ B. (A) π/4 (B) π − 2 (C) (π − 2)/4 (D) 4π (E) π − 4 UNC Charlotte 2005 Comprehensive 6 5. The area of the a × b rectangle shown in the picture below is 5π of the area of b the circle. Assuming b > a, what is the value of a ? ..........................
    [Show full text]
  • Figure It out Number Sense Book 2
    Answers and Teachers’ Notes Introduction 2 Answers 3 contents Teachers’ Notes 10 The books for years 7–8 in the Figure It Out series are issued by the Ministry of Education to provide support material for use in New Zealand year 7–8 classrooms. The books have been developed and trialled by classroom teachers and mathematics educators and follow on from the successful series for levels 2–4 in primary schools. introduction Student books The student books in the series are divided into three curriculum levels: levels 2–3 (linking material), level 4, and level 4+ (extension material). All the books are aimed at year 7–8 students in terms of context and presentation. The following books are included in the series: Number (two linking, three level 4, one level 4+) Number Sense (one linking, one level 4) Algebra (one linking, two level 4, one level 4+) Geometry (one level 4, one level 4+) Measurement (one level 4, one level 4+) Statistics (one level 4, one level 4+) Themes (level 4): Disasters Strike!, Getting Around These 20 books will be distributed to schools with year 7–8 students over a period of two years, starting with the six Number books that were distributed in October 2002. The activities in the student books are set in meaningful contexts, including real-life and imaginary scenarios. The books have been written for New Zealand students, and the contexts reflect their ethnic and cultural diversity and life experiences that are meaningful to students aged 11–13 years. The activities can be used as the focus for teacher-led lessons, as independent bookwork, or as the catalyst for problem solving in groups.
    [Show full text]
  • The Secret Code of God
    The Secret Code of God Abul Hassan Copy Rights and 19 19 – The Secret Code of God By: Abul Hassan 1st Edition: 2010 No Part of this book may be reproduced in any form or by any means electronic, mechanical, photocopying, recording, or otherwise, without the prior written permission of the publisher or author. However any one can download the electronic version of this book, i.e. free eBook from any website on the internet without our permission for the purposes of reading and research or from our website – www.ali-pi.com. Abul Hassan www.ali-pi.com [email protected] [email protected] Price: US$ 19.00/CAN$ 19.00 19 – The Secret Code of God Page 2 Contents and 19 Topics Page 1. Copy Rights and 19 2 2. Abul Hassan’s Desk and 19 5 3. Dedication and 19 7 4. Coding and 19 8 5. Religions of the world and 19 10 6. Bahai’s and 19 11 7. Hinduism and 19 12 8. Symbolism and 19 12 9. Judaism and 19 13 10. Other faiths and 19 16 11. Christianity and 19 17 12. Islam and 19 25 13. Security Code and 19 29 14. Holy Quran and 19 30 15. 99 Names of Allah and 19 73 16. Arabic Alphabets and 19 87 17. Everything and 19 90 18. Mathematics and 19 94 19. Mathematical Properties of 19 97 20. Prime Numbers and 19 102 21. Perfect Numbers and 19 111 22. Powerful Numbers and 19 115 23. Enneadecagon and 19 116 24.
    [Show full text]
  • Numbers 1 to 100
    Numbers 1 to 100 PDF generated using the open source mwlib toolkit. See http://code.pediapress.com/ for more information. PDF generated at: Tue, 30 Nov 2010 02:36:24 UTC Contents Articles −1 (number) 1 0 (number) 3 1 (number) 12 2 (number) 17 3 (number) 23 4 (number) 32 5 (number) 42 6 (number) 50 7 (number) 58 8 (number) 73 9 (number) 77 10 (number) 82 11 (number) 88 12 (number) 94 13 (number) 102 14 (number) 107 15 (number) 111 16 (number) 114 17 (number) 118 18 (number) 124 19 (number) 127 20 (number) 132 21 (number) 136 22 (number) 140 23 (number) 144 24 (number) 148 25 (number) 152 26 (number) 155 27 (number) 158 28 (number) 162 29 (number) 165 30 (number) 168 31 (number) 172 32 (number) 175 33 (number) 179 34 (number) 182 35 (number) 185 36 (number) 188 37 (number) 191 38 (number) 193 39 (number) 196 40 (number) 199 41 (number) 204 42 (number) 207 43 (number) 214 44 (number) 217 45 (number) 220 46 (number) 222 47 (number) 225 48 (number) 229 49 (number) 232 50 (number) 235 51 (number) 238 52 (number) 241 53 (number) 243 54 (number) 246 55 (number) 248 56 (number) 251 57 (number) 255 58 (number) 258 59 (number) 260 60 (number) 263 61 (number) 267 62 (number) 270 63 (number) 272 64 (number) 274 66 (number) 277 67 (number) 280 68 (number) 282 69 (number) 284 70 (number) 286 71 (number) 289 72 (number) 292 73 (number) 296 74 (number) 298 75 (number) 301 77 (number) 302 78 (number) 305 79 (number) 307 80 (number) 309 81 (number) 311 82 (number) 313 83 (number) 315 84 (number) 318 85 (number) 320 86 (number) 323 87 (number) 326 88 (number)
    [Show full text]
  • UNC Charlotte 2005 Comprehensive March 7, 2005
    UNC Charlotte 2005 Comprehensive March 7, 2005 1. The numbers x and y satisfy 2x = 15 and 15y = 32. What is the value xy? (A) 3 (B) 4 (C) 5 (D) 6 (E) none of A, B, C or D Solution: C. Note that (2x)y = 15y = 32 so 2xy = 25 and xy = 5. 2. Suppose x, y, z, and w are real numbers satisfying x/y = 4/7, y/z = 14/3, and z/w = 3/11. When (x + y + z)/w is written in the form m/n where m and n are positive integers with no common divisors bigger than 1, what is m + n? (A) 20 (B) 26 (C) 32 (D) 36 (E) 37 Solution: D. Calculate x/w, y/w and compute the sum. For example, x/w = 4/7 · 14/3 · 3/11 = 8/11 and y/w = 14/3 · 3/11 = 14/11, so (x + y + z)/w = (8 + 14 + 3)/11. 3. Let m be an integer such that 1 ≤ m ≤ 1000. Find the probability of selecting at random an integer m such that the quadratic equation 6x2 − 5mx + m2 = 0 has at least one integer solution. (A) 0.333 (B) 0.5 (C) 0.667 (D) 0.778 (E) 0.883 Solution: C. The quadratic equation has two solutions m x = 2 m x = 3 There are 500 multiples of 2, 333 multiples of 3, and 166 multiples of 6 between 1 and 1000. Therefore, the probability is 500 + 333 − 166 p = = 0.667 1000 4. Let z = x + iy be a complex number, where x and y are real numbers.
    [Show full text]
  • Numerical Methods, Mathematics in Daily Life and Study of Indian Mathematician
    International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056 Volume: 07 Issue: 04 | Apr 2020 www.irjet.net p-ISSN: 2395-0072 Numerical Methods, Mathematics in Daily Life and Study of Indian Mathematician Tejaswini Smita Sanjay Sawant1, Sujata Milind Gupte 2, Rizvi Syed Ismat Fatima3 1Tejaswini Smita Sanjay Sawant, VPM's Polytechnic Thane, Maharashtra, India 2Sujata Milind Gupte, VPM's Polytechnic Thane, Maharashtra, India 3Rizvi Syed Ismat Fatima, VPM's Polytechnic Thane, Maharashtra, India ---------------------------------------------------------------------***---------------------------------------------------------------------- Abstract - In this journal we study numerical methods and the NUMERICAL INTEGRATION: uses of mathematics in our daily life. Most of the time students are considering the mathematics is not important in current The computation of definite integral from the set of or future life. Mathematics is not only use in daily life but also numerical values of the integrand is called numerical essential part of our lives. The different methods of finding integration. approximately numerical solutions through the computation are called numerical methods. According to some people, Mathamatics is just the use of complicated formulas, The three formulae for numerical integration are derivations, Calculations which won’t be ever applied in real (1) Trapezoidal rule: life. But, Mathamatics is the universal language which is The interval [a,b] is divided into n(even or applied in almost every aspect of life. Basic mathematical odd)number of sub-intervals of equal width, then concepts are followed in every day our life. You would be amazed to see the emerging of maths from unexpected situations. Key Words: Numerical methods, Mathematics, Universal language, Daily life.
    [Show full text]
  • A Crossnumber Meta: Nose Functions
    A CROSSNUMBER META: NOSE FUNCTIONS 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 NOSE FUNCTIONS: A CROSSNUMBER: PAGE 1/3 In the clues below, n represents the number being clued and k and m represent unspecified positive integers. In neither case is there a connection between these values in different clues. Across 1. the smallest conductor of an elliptic curve over the rational numbers 3. the sum of the first k Sophie Germain primes 8. (the number of primes between two consecutive powers of 2) + (the floor of (k=e)k=e) 10. a divisor of 99999999 11. an even non-totient number 12. (a tribonacci number) + (the number of conjugacy classes in GL8(F2)) 13. 2n contains no zeros 14. (the average of the divisors of n is itself a divisor of n) + (a semiprime tribonacci number) 15. a palindrome with exactly 5 palindromic prime factors (counted with multiplicity) 16. a sum of four consecutive cubes 17. the kissing number in dimension 4 19. the number of permutations of length k with exactly 2 distinct cycle lengths (e.g. any transposition) 21. a palindromic even semiprime not expressible as the sum of two squares 22. a repdigit in base 10 that is also a repdigit when expressed in some smaller base larger than 1. Down 1. (a Sophie Germain prime equal to the sum of the first k Sophie Germain primes) · (the number of directed graphs with m unlabeled vertices and no self-loops or multiple edges in the same direction) 2.
    [Show full text]
  • Some Properties of the Kaprekar Numbers and a Means of Generation
    R ESEARCH ARTICLE ScienceAsia 27 (2001) : 133-136 Some Properties of the Kaprekar Numbers and a Means of Generation Colin G Black Mechanical Engineering Program, Sirindhorn International Institute of Technology at Thammasat University, Pathum Thani 12121, Thailand. Corresponding author, E-mail: [email protected] Received 31 Jul 2000 Accepted 26 Jan 2001 ABSTRACT This note describes what is believed to be a novel and easily implemented method for generating integer Kaprekar numbers. The starting point for the method is the observation made here, that a necessary condition for an integer k to be a Kaprekar number is that k must be congruent to k2 modulo-9. Moreover, it is also shown here that a Kaprekar number k is either a member of the residue class [0] or residue class [1] modulo-9. For an integer k congruent to k2 modulo-9, further steps are then established to find any integer values: q, r and n, such that k = q + r, and k2 = q x 10n + r. The method described here is implemented using the computer algebra software package: Mathcad. A list of the entire integer Kaprekar numbers lying between 1 and 106 is generated. In addition, some results relating to the properties of the Kaprekar numbers are also presented. KEYWORDS: Kapreka numbers, modulo arithmetic, congruent. INTRODUCTION In fact, 9, 55 and 95121 are 1-Kaprekar, 2-Kaprekar and 5-Kaprekar numbers, respectively. The n-Kaprekar numbers are named after DR Kaprekar, who first introduced them in 1980.1 They In this note, a new scheme for generating all the are formally defined as follows: an n-Kaprekar n-Kaprekar numbers less than or equal to a specified number k 1 (n = 1,2, …) satisfies the pair of value is obtained.
    [Show full text]
  • A Set of Mathematical Equivoques Ken Suman, [email protected]
    A Set of Mathematical Equivoques Ken Suman [email protected] last updated on 1/7/2007 A 9 12 Abelian – 10 or 10 depending on whether you studied math or maths at school Abscissa – a person who is self absorbed with their abs Absolute Geometry – geometry that doesn’t play fair Absolute Value – nonnegotiable price Absorbing State – “You can check in any time you like, but you can never leave.” Abundant Number – a lot Acceptance Sampling – launching a trial balloon Acousmatic – someone who is quick to point fingers Adding Machine – a good summer Additive Identity – alias Adèle Group – the Astaire’s Adenine – nucleotide that tells us how to go from 1 to 10 Adiabatic Law – always monitor your glucose level Affine Variety – what a good store carries Agonic – someone who lives in the past Airport Problem – when you lose your in flight internet connection Page 1 A Set of Mathematical Equivoques Ken Suman, [email protected] Alethic – stout Alexander Polynomial – Iksander, Richard Burton, Colin Farrell, but apparently not Leonardo DiCaprio ALGOL – what Julius Caesar divided into three parts Aliorelative – onion Aliter – a little more than a quart Aliquot – “float like a butterfly, sting like a bee” Allegory – Tipper’s husband when in Rome Almost Surely – Shirley Almost Everywhere – where kudzu grows Alternating Group – Animagi Alternation – Vatican City Amenable Group – The Beatles Amicable Pair – good friends Amphibology – switch pitching Analemma Curve – slant eight Anallagmatic – Wrangler blue jeans Analysis – denouement Analysis of Variance
    [Show full text]
  • Proceedings Cover
    Sharing Mathematics A tribute to Jim Totten Editors Richard C. Brewster John Grant McLoughlin May 13–15, 2009 Thompson Rivers University, Kamloops, BC Sharing Mathematics – A tribute to Jim Totten, Conference Proceedings Edited by Richard C Brewster & John Grant McLoughlin The copyright for each article is held by the respective presenter. This program is made available under a Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 Unported Canada License. Printed by the Thompson Rivers University Printshop. c Richard C Brewster, John Grant McLoughlin, 2010 ! Contents Editors’ note .................................................................v Plenary Talks ..................................................................1 A Mathematical Musing: Wonder, Elegance and Beauty of Numbers John Grant McLoughlin . 3 Hands-free Teaching Jennifer Hyndman . 13 Some New Initiatives at Math Central Harley Weston . .19 Contributed Papers ..........................................................23 Mathematical engagement: Moving beyond the classroom Richard C. Brewster, Susan Kinniburgh, Laura Teshima . 25 Preliminary Research Report: The Relationship Between Missing Graded Homework and Student Outcomes in Undergraduate Math Courses Lorraine Dame, Michelle Edwards, Gary MacGillivray . 32 Motivating Conceptual Learning Through Mathematical Misconcep- tions Nora Franzova, John Grant McLoughlin . 44 Mathematics and Critical Thinking Lee Keener . 50 The British Columbia Secondary School Mathematics Contest Clint Lee........................................................................54
    [Show full text]