Development of Prefabricated Timber-Concrete Composite Floors
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Concrete Support Structures for Offshore Wind Turbines: Current Status, Challenges, and Future Trends
energies Review Concrete Support Structures for Offshore Wind Turbines: Current Status, Challenges, and Future Trends Alexandre Mathern 1,2,* , Christoph von der Haar 3 and Steffen Marx 4 1 Department of Architecture and Civil Engineering, Chalmers University of Technology, Sven Hultins Gata 6, SE-41296 Gothenburg, Sweden 2 Research and Innovation, NCC AB, Lilla Bomen 3c, SE-41104 Gothenburg, Sweden 3 grbv Ingenieure im Bauwesen GmbH & Co. KG, Expo Plaza 10, 30539 Hannover, Germany; [email protected] 4 Institute of Concrete Structures, Technische Universität Dresden, August-Bebel-Straße 30/30A, 01219 Dresden, Germany; [email protected] * Correspondence: [email protected] or [email protected] Abstract: Today’s offshore wind turbine support structures market is largely dominated by steel structures, since steel monopiles account for the vast majority of installations in the last decade and new types of multi-leg steel structures have been developed in recent years. However, as wind turbines become bigger, and potential sites for offshore wind farms are located in ever deeper waters and ever further from the shore, the conditions for the design, transport, and installation of support structures are changing. In light of these facts, this paper identifies and categorizes the challenges and future trends related to the use of concrete for support structures of future offshore wind projects. To do so, recent advances and technologies still under development for both bottom-fixed and floating concrete support structures have been reviewed. It was found that these new developments meet the Citation: Mathern, A.; von der Haar, challenges associated with the use of concrete support structures, as they will allow the production C.; Marx, S. -

CRSI-Design Guide for Voided Concrete Slabs
Addendum – Design Guide for Voided Concrete Slabs Supplemental Information for the First Edition Printing Featuring New and Updated Voided Slab Design Considerations, and Project Case Studies. Concrete Reinforcing Steel Institute 2019 Founded in 1924, the Concrete Reinforcing Steel Institute (CRSI) is a technical institute and an ANSI-accredited Standards Developing Organization (SDO) that stands as the authoritative resource for information related to steel reinforced concrete construction. Serving the needs of engineers, architects and construction professionals, CRSI offers many industry-trusted technical publications, standards documents, design aids, reference materials and educational opportunities. CRSI Industry members include manufacturers, fabricators, material suppliers and placers of steel reinforcing bars and related products. Our Professional members are involved in the research, design, and construction of steel reinforced concrete. CRSI also has a broad Region Manager network that supports both members and industry professionals and creates awareness among the design/construction community through outreach activities. Together, they form a complete network of industry information and support. Design Guide for Voided Concrete Slabs – Addendum Overview This addendum contains revised content to the first edition of this Design Guide. In particular, the following items are new or have been updated (denoted in bold text on the Contents page): 1. New information and design aids on vibration analysis in Section 3.6.3. 2. Updated information on fire resistance in Section 3.7. 3. The example in Section 3.9 has been updated to the provisions of ACI 318-14, and now includes headed shear stud design. 4. Updated information on concrete placement in Section 4.1. 5. Updated specifications in Section 5.2. -

Concrete 2021 Program Book
5–8 September 2021 • Virtual Conference Smart & Innovative Concrete from Disruption 30TH BIENNIAL NATIONAL CONFERENCE OF THE CONCRETE INSTITUTE OF AUSTRALIA PROGRAM BOOK www.ciaconference.com.au #inthemix #Concrete2021 CONFERENCE PARTNERS The Organising Committee for the Concrete 2021 Conference extends its appreciation to the following partners for their invaluable commitment and support: Sika Australia Fosroc ANZ Ramset, Reid, Danley Major Partner Major Partner Major Partner Leviat Duratec Australia Bluey Technologies Supporting Partner Supporting Partner Supporting Partner BCRC BG&E Master Builders Solutions Invited Speaker Partner Keynote Speaker Partner Keynote Speaker Partner - Mr Oscar Antommattei - Dr Stuart Matthews - Dr Kefei Li Aptus SRIA National Precast Partner Advertising Partner Advertising Partner BOSFA Madewell Products Mapei PCTE Exhibitor Exhibitor Exhibitor Exhibitor VIRTUAL CONFERENCE PROGRAM BOOK P2 CONFERENCE CHAIR’S MESSAGE WELCOME! As the Conference Chair for the Concrete Institute of Australia’s Biennial National Conference, Concrete 2021, it is my pleasure to have you join us virtually from 5 – 8 September 2021. You will experience an engaging and exciting virtual program including keynote speakers, invited speakers and over 140 technical presentations. This year you can plan the program around your own schedule giving you greater access to more presentations than ever before – what’s even better is you will have access to 100% of the program content, on demand post Conference! Engage through virtual networking with industry leaders and strengthen your professional contacts as a part of our dynamic online community to create new industry contacts. Under the theme “Smart & Innovative Concrete from Disruption” the Conference is covering all aspects of concrete materials, design, construction, repair, and maintenance. -

Injection 3D Concrete Printing (I3DCP): Basic Principles and Case Studies
materials Article Injection 3D Concrete Printing (I3DCP): Basic Principles and Case Studies Norman Hack 1,* , Inka Dressler 2 , Leon Brohmann 1, Stefan Gantner 1, Dirk Lowke 2 and Harald Kloft 1 1 Institute of Structural Design, Technische Universität Braunschweig, Pockelsstr. 4, 38104 Braunschweig, Germany; [email protected] (L.B.); [email protected] (S.G.); [email protected] (H.K.) 2 Institute of Building Materials, Concrete Construction and Fire Safety, Technische Universität Braunschweig, Beethovenstr. 52, 38106 Braunschweig, Germany; [email protected] (I.D.); [email protected] (D.L.) * Correspondence: [email protected] Received: 25 January 2020; Accepted: 27 February 2020; Published: 1 March 2020 Abstract: Today, the majority of research in 3D concrete printing focuses on one of the three methods: firstly, material extrusion; secondly, particle-bed binding; and thirdly, material jetting. Common to all these technologies is that the material is applied in horizontal layers. In this paper, a novel 3D concrete printing technology is presented which challenges this principle: the so-called Injection 3D Concrete Printing (I3DCP) technology is based on the concept that a fluid material (M1) is robotically injected into a material (M2) with specific rheological properties, causing material M1 to maintain a stable position within material M2. Different to the layered deposition of horizontal strands, intricate concrete structures can be created through printing spatially free trajectories, that are unconstrained by gravitational forces during printing. In this paper, three versions of this method were investigated, described, and evaluated for their potential in construction: A) injecting a fine grain concrete into a non-hardening suspension; B) injecting a non-hardening suspension into a fine grain concrete; and C) injecting a fine grain concrete with specific properties into a fine grain concrete with different properties. -

Design of Concrete Buildings
EUROCODE 2: BACKGROUND & APPLICATIONS DESIGN OF CONCRETE BUILDINGS Worked examples Authors: F.Biasioli, G.Mancini, M.Just, M.Curbach, J.Walraven, S.Gmainer, J.Arrieta, R.Frank, C.Morin, F.Robert Editors: F.Biasioli, M.Poljanšek, B.Nikolova, S.Dimova, A.Pinto 2014 ReportReport EUR EUR xxxxx 26566 EN EN European Commission Joint Research Centre Institute for the Protection and Security of the Citizen Contact information Address: Joint Research Centre, Via Enrico Fermi 2749, TP 480, 21027 Ispra (VA), Italy E-mail: [email protected] Tel.: +39 0332 78 9989 Fax: +39 0332 78 9049 http://ipsc.jrc.ec.europa.eu/ http://www.jrc.ec.europa.eu/ Legal Notice Neither the European Commission nor any person acting on behalf of the Commission is responsible for the use which might be made of this publication. Europe Direct is a service to help you find answers to your questions about the European Union Freephone number (*): 00 800 6 7 8 9 10 11 (*) Certain mobile telephone operators do not allow access to 00 800 numbers or these calls may be billed. A great deal of additional information on the European Union is available on the Internet. It can be accessed through the Europa server http://europa.eu/. JRC89037 EUR 26566 EN ISBN 978-92-79-36548-5 ISSN 1831-9424 doi:10.2788/35386 Luxembourg: Publications Office of the European Union, 2014 © European Union, 2014 Reproduction is authorised provided the source is acknowledged. Printed in Italy Contents List of authors and editors ....................................................................................................... vii Foreword ..................................................................................................................................... ix CHAPTER 1 .................................................................................................................................. 1 CONCEPTUAL AND PRELIMINARY DESIGN 1.1 Introduction ....................................................................................................................... -
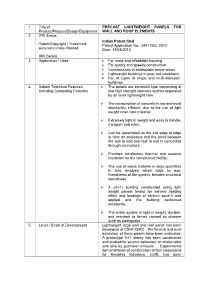
1. Title of Product/Process/Design/Equipment
1. Title of PRECAST LIGHTWEIGHT PANELS FOR Product/Process/Design/Equipment WALL AND ROOF ELEMENTS 2. IPR Status Indian Patent filed Patent/Copyright / Trademark Patent Application No.: 2441 DEL 2013 secured in India /Abroad Date: 19/08/2013 IPR Details 3. Application / Uses For mass and affordable housing For quality and speedy construction Constructions in earthquake prone areas Lightweight buildings in poor soil conditions For all types of single and multi-storeyed buildings 4. Salient Technical Features The panels are sandwich type comprising of including Competing Features two high strength concrete wythes separated by an inner lightweight core The consumption of concrete is low and most structurally efficient, due to the use of light weight inner core material Extremely light in weight and easy to handle, transport and erect. Can be assembled on the site edge to edge to form an enclosure and the joints between the wall to wall and roof to wall is connected through connectors. Provides satisfactory thermal and acoustic insulation for the constructed facility. The use of waste material in large quantities is also involved which adds to eco- friendliness of the system, besides structural soundness A (G+1) building constructed using light weight panels tested for seismic loading effect and loadings of seismic zone-5 was applied and the building performed excellently. The entire system is light in weight, durable, and resistant to forces caused by disaster such as earthquake. 5. Level / Scale of Development Lightweight large wall and roof panel has been developed at CSIR-SERC. The flexural and axial behaviour of these panels have been evaluated. -

Product Comparison.Pdf
Introduction to BubbleDeck BubbleDeck® is a pre-fabricated structure with superior characteristics to solid slab. Plastic balls serve the purpose of eliminating concrete which has weight but no carrying effect. BubbleDeck can reduce construction material weight up to 50%. ECONOMIC ADVANTAGES The amount of materials - concrete, columns, rebar, transfer beams and other materials is reduced by up to 50%: 1 kg recycled plastic replaces 100 kg concrete. Slabs are factory produced and shipped to site as required. Transportation costs are substantially reduced. Shoring is considerably reduced and BubbleDeck slabs replace expensive formwork. Pre-fabrication and easy installation result in faster construction time. Less man hours equals lower costs and overhead. Clients get a design they want for a better price. Interior finishing is less costly. Life span of buildings is greater. The potential saving of a building designed in BubbleDeck is 25% of the structural cost. SUPERIOR DESIGN BubbleDeck allows for superior design flexibility - dramatic architectual shapes, larger spans and overhangs.No dr op beams or carrying walls and fewer columns are required allowing for spa- cious and flexible interior layouts. Interior layouts are easily altered throughout a BubbleDeck building's lifetime. BubbleDeck conforms to engineering designs and building codes, has less weight and less seismic load. Build what you want not what you must - BubbleDeck has you thinking outside the box. THE GREEN DECK Less energy consumption - in production, transportation and construction. Less emissions - ex- haust gases and vapors during production, transport and on-site; (CO2 and other emissions - re- duced up to 50%). Less material consumption - cement, aggregates, water, steel. -

Development of Novel Low-Clinker High-Performance Concrete Elements Prestressed with High Modulus Carbon Fibre Reinforced Polymers
Development of novel low-clinker high-performance concrete elements prestressed with high modulus carbon fibre reinforced polymers DISS. ETH NO. – 25890 Tobias Dominik Lämmlein March 2019 Empa – Mechanical Systems Engineering Laboratory ETH Zurich – Institute for Building Materials (IfB) DISS. ETH NO. – 25890 Development of novel low-clinker high-performance concrete elements prestressed with high modulus carbon fibre reinforced polymers A thesis submitted to attain the degree of DOCTOR OF SCIENCES of ETH ZURICH (Dr. sc. ETH Zurich) presented by TOBIAS DOMINIK LÄMMLEIN MSc ETH ME, ETH Zurich born on 20.09.1985 citizen of Germany accepted on the recommendation of Prof. Dr. Pietro Lura Dr. Giovanni P. Terrasi Prof. Dr. Janet M. Lees Prof. Dr. Guillaume Habert 2019 Acknowledgements Firstly, I`d like to thank both of my excellent supervisors Prof. Dr. P. Lura and Dr. G. P. Terrasi for their great guidance, their continuous support and their never-ending inspiration during many talks and steps of this Thesis. Further, I would like to express my gratitude to Prof. Dr. J. M. Lees and Prof. Dr. G. Habert for serving in my PhD committee and their support during the final stage of this Thesis. A special thanks goes to Dr. Michele Griffa, Lee Völker, Vanessa Rohr, Iurii Burda, Francesco Messina and Dr. Mateusz Wyrzykowski for their direct support of this Thesis and their fruitful discussions and inputs. Moreover, I would like to thank the whole work group in the joint Concrete Solution project. Especially, I would like to address my gratitude to Sharon Zingg and Francesco Pittau for managing the project and their support while performing the LCA analysis. -

Review on Bubble Deck Slabs Technology and Their Applications
INTERNATIONAL JOURNAL OF SCIENTIFIC & TECHNOLOGY RESEARCH VOLUME 8, ISSUE 10, OCTOBER 2019 ISSN 2277-8616 Review On Bubble Deck Slabs Technology And Their Applications Samantha.Konuri, Dr.T.V.S.Varalakshmi Abstract: A structural system of Tremendous importance in constructions are slabs or floor systems, it is called two dimensional slab structural elements, where the third dimension is small compared with the other two basic dimensions. Loads acting perpendicular slabs, to the flat principal, may be from different shapes Y configurations relying on the need for which apply at all times seeks to make them lighter but covering the greatest possible distances and always seeking to improve productivity and energy savings in construction. A widely used type slabs are currently slabs reinforced concrete, these systems have several advantages such as high resistance to compressive stresses and flexural actions, in addition to a particularly low value in the construction of the elements. However, it has certain disadvantages in terms of weight and maintenance of structures, renovation in large- scale constructions. In this area, the mid-20th century systems relieved hollow concrete slabs were created in order to reduce high ratios weight- resistance of conventional systems. These systems reduce or change the concrete within the middle of the slab by a lighter material to from reduce the weight own from the structure. But nevertheless these relieved as in slabs reduce the strength thereof before exposure to shear forces and fire. In the early 90s German engineer Jorgen Breuning found a way to improve these drawbacks in slabs, linking the air space, steel and concrete in a hollow slab bidirectional, using spheres made of plastic thus giving rise to the BDT. -

Structural Design of Underground Garage - Breadth
Residence Inn By Marriott 2345 Mill Rd, Alexandria, VA Julia E. Phillips Construction Management Analysis 1: Structural Design of Underground Garage - Breadth Background The underground garage is entirely constructed of cast in place concrete with an 8” slab and 5.5” drop panels at the columns totaling a 13.5” slab at the deepest sections. The cast in place floor area was averaged to 14,700 SF per floor. The rebar in the beams was estimated by the specifications in the drawings by using 2/3 the length of the beam for the top rebar and the full length for the bottom rebar. An original floor plan can be found in Appendix D. This system was designed to minimize the floor depth, to be able to help maximize the total number of floors in the building, enabling construction of 15 floors compared to 14 floors. Unexpected water problems associated with excavation pushed the project behind schedule. The added time for curing the cast in place concrete to the full 28 day strength only slowed the project more. The project has a relatively tight schedule of approximately a year and a half, so any time that can be saved once the schedule is behind, needs to be saved or the project will not finish on time. One possible solution is to switch the cast in place concrete to a Filigree concrete system. Filigree virtually eliminates formwork and is very easy and quick to install. This system uses a small amount of shoring to support the pre-stressed prefabricated Filigree panels. The Filigree panels once supported act as the “formwork” for the topping slab that ties the system together structurally. -

Mpact S T I U E S T I U E
Re-con Zero.pdf 1 5/22/2013 9:15:33 AM S S I I N N G G A A P P O O R R E E C C O O N N C C R R E E T T E E I I N N S S T T I I T T U U T T Returned Concrete at Zero Impact E E STEP STEP 1155 NNOOVV 1133 •• MMIICCAA ((PP)) NNoo.. 005511//OO99//22001133 VVooll 55 NNoo 11 Component B Component A 6 kg/m3 3 Mix for 0.5 kg/m 3 minutes Mix for 1 kg 1 kg 1 kg 4 minutes 0.5 kg 1 kg 1 kg 1 kg C M S S C C I I Y C C O O N N STEP C C R R CM E E T T U U S S MY • • CONCRETE V V o o l l CY 5 5 N N o o 1 1 CMY K DISCHARGE RE-CON ZERØ The innovative product for the sustainable recovery of returned concrete • No waste produced • Added directly into the truck mixer • No treatment plants required • Re-usable aggregate for concrete • Minimize environment impact 1 1 5 5 N N • Reduce overall operating cost O O V V 1 1 3 3 • • Discover our world of Mapei: www.mapei.com.sg M M I I C C A A ( ( P P ) ) N N Mapei Far East Pte Ltd o o . 28 Tuas West Road, Singapore 638383 0 0 SSIINNGGAAPPOORREE 5 5 1 1 Tel: +65 68623488 Fax: +65 68621012/13 / / 0 0 9 9 CCOONNCCRREETTEE Website: www.mapei.com.sg Email: [email protected] / / 2 2 0 0 1 1 3 3 IINNSSTTIITTUUTTEE CONTENTS PRESIDENT’S MESSAGE 2 BOARD OF DIRECTORS 2013/2014 3 CATEGORY 1: CONCRETE TECHNOLOGIES AND STANDARDS • If Concrete Can Speak – Health Testing 4 • Thermal behaviour of concrete mixes with diff erent pozzolanic additions 5 SCI Concretus CATEGORY 2: STRUCTURAL HEALTH MONITORING, TESTING AND REPAIR Issue 5.1 Nov 2013 • Investigation and Repair Advisory Services 10 www.SCI-Concretus.com • SilverSchmidt Hammer 13 Honorary Chief Editor • DY‐2 Family Pull-off Tester 13 Dr. -

Channels and Accessories
REINFORCEMENT FACADE CONNECTION FASTENING TECHNOLOGY TECHNOLOGY CONNECTOR TECHNOLOGY SYSTEMS MOUNTING TECHNOLOGY Channels and Accessories JORDAHL® Channels and Accessories Making Light Work of the Heaviest Loads. Technical Information anchored in quality FASTENING TECHNOLOGY REINFORCEMENT FACADE CONNECTION FASTENING TECHNOLOGY TECHNOLOGY CONNECTOR TECHNOLOGY SYSTEMS MOUNTING TECHNOLOGY Quality Since 1907 JORDAHL – The Company JORDAHL connects: steel, heavy loads, and a whole lot more. Many customers around the world have already decided on high-quality products for fastening, reinforcement, shear connections, framing, and facade connection systems. Customers who choose JORDAHL want more – higher quality, broader choice, better consulting services, wider experience. They get all of this from JORDAHL. Since our company was founded in Germany in 1907, we have been at the forefront of connection and shear reinforcement system development. JORDAHL products, such as anchor channels, have become milestones in the evolution of structural engineering and have brought lasting changes to construction, shaping the way buildings are designed and making them safer, around the world. JORDAHL’s registered office and administrative headquarters in Berlin JORDAHL Advice We not only set high standards with our products, but with technical consultation as well. Our competent and experienced JORDAHL experts are always aware of the latest developments and offer modern, flexible, and customised solutions to cater to all your needs. The more than 700 emails and calls to JORDAHL experts every day at our technical department in Berlin show just how much our customers appreciate the advice. We have more than 50 engineers available around the world, who can also develop the right solution for your very specific application.