DOCSLIB.ORG

Chapter 8 Natural and Step Responses of RLC Circuits

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter 8 Natural and Step Responses of RLC Circuits Chapter 8 Natural and Step Responses of RLC Circuits 8.1-2 The Natural Response of a Parallel RLC Circuit 8.3 The Step Response of a Parallel RLC Circuit 8.4 The Natural and Step Response of a Series RLC Circuit 1 Key points What do the response curves of over-, under-, and critically-damped circuits look like? How to choose R, L, C values to achieve fast switching or to prevent overshooting damage? What are the initial conditions in an RLC circuit? How to use them to determine the expansion coefficients of the complete solution? Comparisons between: (1) natural & step responses, (2) parallel, series, or general RLC. 2 Section 8.1, 8.2 The Natural Response of a Parallel RLC Circuit 1. ODE, ICs, general solution of parallel voltage 2. Over-damped response 3. Under-damped response 4. Critically-damped response 3 The governing ordinary differential equation (ODE) V0, I0, v(t) must satisfy the passive sign convention. dv 1 t v By KCL: C I0 v() t d t 0 . 0 dt L R Perform time derivative, we got a linear 2nd- E of order ODv(t) with constant coefficients: d2 v 1 dv v 0 . dt2 RCdt LC 4 The two initial conditions (ICs) The capacitor voltage cannot change abruptly, (v 0 ) V0 ( 1 ) The inductor current cannot change abruptly, ( 0i )L I, i 0 (C 0 ) iL ( i 0R ) 0 ( I 0 0 V ) , R dvC I0V 0 i(C 0 ) C, v(C 0 ) v ( 0 ) ( 2 ) dt t0 C RC 5 General solution Assume the solution vis () t Ae st , where A, s are unknown constants to be solved. Substitute into the ODE, we got an algebraic (characteristic) equation of s determined by the circuit parameters: s 1 s2 0 . RC LC Since the ODE is linear, linear combination of solutions remains a solution to the equation. The general solution of v(t) must be of the form: s1 t s2 t v t() A1 e 2 A, e where the expansion constants A1, A2 will be determined by the two initial conditions. 6 Neper and resonance frequencies In general, s has two roots, which can be (1) distinct real, (2) degenerate real, or (3) complex conjugate pair. 2 1 1 1 2 2 1s , 2 0 , 2RC RC 2 LC where 1 , …neper frequency 2RC 1 …resonance (natural) frequency 0 LC 7 Three types of natural response How the circuit reaches its steady state depends on the relative magnitudes of and 0: The Circuit is When Solutions real, distinct Over-damped roots s1, s2 complex roots Under-damped * s1 = (s2) real, equal roots Critically-damped s1 = s2 8 Over-damped response ( >0) The complete solution and its derivative are of the form: s1 t s2 t v t () A1 e 2 A, e s1 t s2 t v t () A1 s 1 e 2 A 2 . s e 2 2 where 1s , 2 0 are distinct real. Substitute the two ICs: v( 0 A ) A ( V 1 ) 1 2 0 solve I0V 0 A1, A2. v( 0 s )1 A 1 2 s 2 A ( 2 ) C RC 9 Example 8.2: Discharging a parallel RLC circuit (1) Q: v(t), iC( t), iL( t), iR( t)=? 12 V 30 mA 1 1 12 . 5 kHz ,> , 22 (RC 200 )( 27 10 ) 0 over- 1 1 10 kHz.damped 0 2 7 (LC 5 10 )( 2 10 ) 10 Example 8.2: Solving the parameters (2) The 2 distinct real roots of s are: 2 2 s 1 50 kHz …|s1|< , (slow) 2 2 …|s |>(fast) s 2 200 kHz 2 . The 2 expansion coefficients are: AAV1 2 0 AA 1 2 12 I0V 0 s1 A 1 s 2 A2 5AA 1 20 2 450 C RC 14A1 V ,A2 26 V. 11 Example 8.2: The parallel voltage evolution (3) s1 t s2 t 5000t 20000t v t() A e1 A2 e 14 26 e e V. |s2|>(fast) Converge dominates to zero “Over” |s1|<(slow) damp dominates 12 Example 8.2: The branch currents evolution (4) The branch current through R is: v() t i() t 70e5000130t e20000t mA. R 200 The branch current through L is: t 1 5000t 20000t ( )iL t 30 mA v( t ) d t 56 e26 e mA. 5 0 mH0 The branch current through C is: dv ( )i ( t 0 . 2μ F)14e5000104t e20000t mA. C dt 13 Example 8.2: The branch currents evolution (5) Converge to zero 14 General solution to under-damped response ( <0) The two roots of s are complex conjugate pair: 2 2 1s , 2 0 j d , 2 2 where d 0 is the damped frequency. The general solution is reformulated as: ()j d t ()j d t v() t A1 e A2 e t e A1cos td jsin d t 2 Acosd sin td j t t e A1 A 2 cosd t j1 A 2 sin Ad t t e B1 cosd t 2sin Bd . t 15 Solving the expansion coefficients B1, B2 by ICs The derivative of v(t) is: t t v t() B1 ecos d t d sin ed t t t B2 esin d t d ecos d t t e B 1 Bd 2 cos d t 2 B d 1 sin Bd . t Substitute the two ICs: v( 0 ) B V( 1 ) 1 0 solve I V 0 0 B , B . (v 0 )BB 1 d 2 ( 2 ) 1 2 C RC 16 Example 8.4: Discharging a parallel RLC circuit (1) Q: v(t), iC( t), iL( t), iR( t)=? 0 V -12.25 mA 1 1 0 . 2 kHz , 4 7 < , 2 (2 RC 10 )( 1 . 25 10 ) 0 1 1 under- 1 kHz. 0 7 damped (LC 8 )( 1 . 25 10 ) 17 Example 8.4: Solving the parameters (2) The damped frequency is: 2 2 2 2 d 1 0 0 . 2 0 . 98 kHz . The 2 expansion coefficients are: BV 10 0 ( 1 ) B1 0 , I0V 0 BB 1 d 2 ( 2 ) B2100 V C RC 18 Example 8.4: The parallel voltage evolution (3) t t 200t v t() B e1 cosd t 2 B100sin ed t sin e 980t V . The voltage oscillates (~d ) and approaches the final value (~), different from the over- damped case (no oscillation, 2 decay constants). 19 Example 8.4: The branch currents evolutions (4) The three branch currents are: 20 Rules for circuit designers If one desires the circuit reaches the final value as fast as possible while the minor oscillation is of less concern, choosing R, L, C values to satisfy under-damped condition. If one concerns that the response not exceed its final value to prevent potential damage, designing the system to be over-damped at the cost of slower response. 21 General solution to critically-damped response (=0) Two identical real roots of s make st st st st vtAe() 1 Ae2 (),1 A 2 Ae0 Ae not possible to satisfy 2 independent ICs (V0, I0) with a single expansion constant A0. The general solution is reformulated as: t v t() e D1 t 2. D You can prove the validity of this form by substituting it into the ODE: v()( t RC ) ()(1 v t 1 LC )()0. v t 22 Solving the expansion coefficients D1, D2 by ICs The derivative of v(t) is: t t t t v t D() e1 te D 2 e 1 D 2 D1 . D t e Substitute the two ICs: v( 0 ) D V( 1 ) 2 0 solve D , D . I0V 0 1 2 v( 0 ) D 1 2 D ( 2 ) C RC 23 Example 8.5: Discharging a parallel RLC circuit (1) Q: What is R such that the circuit is critically- damped? Plot the corresponding v(t). R 0 V -12.25 mA 1 1 1 L 1 8 , , R 4 k . 0 2RC LC 2 C 12 . 25 7 10 Increasing R tends to bring the circuit from over- to critically- nd even under-damped. a 24 Example 8.5: Solving the parameters (2) The neper frequency is: 1 1 1 kHz , 2 (2 4RC 10 )(3 1 . 257 10 ) 1 1 ms. The 2 expansion coefficients are: DV 20 0 ( 1 ) -12.25 mA D981 kV s I0V 0 DD1 2 ( 2 ) D2 0 C RC 0.125 F 25 Example 8.5: The parallel voltage evolution (3) t t 1000t v t() D1 te 298 D , e 000te V . 98 V/ms 26 Procedures of solving nature response of parallel RLC 1 Calculate parameters ( 2 RC ) and 0 1 LC. Write the form of v(t) by comparing and : A es1 t A, s2 e t s - 2 , 2 if , 1 2 1 , 2 0 0 t 2 2 v() te B1 cosd t sin2 B d , td 0 , if 0 , et D t, Dif . 1 2 0 Find the expansion constants (A1, A2), (B1, B2), or (D1, D2) by two ICs:(v 0 ) V ( 1 ), 0 I0V 0 (v 0 ) ( 2 ) C RC 27 Section 8.3 The Step Response of a Parallel RLC Circuit 1. Inhomogeneous ODE, ICs, and general solution 28 The homogeneous ODE + Is V0 I0 dv 1 t v By KCL: C I0 v() t d t Is. 0 dt L R Perform time derivative, we got a homogeneous ODE of v(t) independent of the source current Is: 2 d v 1 dv v 0 . dt2 RCdt LC 29 The inhomogeneous ODE i Is L V0 I0 Change the unknown to the inductor current iL( t): dv v C i I , dt L R s d2 i 1 di i I L L L s di dt2 RCdt LC LC v L L , dt 30 The two initial conditions (ICs) i Is L V0 I0 The inductor current cannot change abruptly, (i 0L ) I0 ( 1 ) The capacitor voltage cannot change abruptly, (v 0C ) V0 L ( v 0 ), diL V0 ( 0v )L L , i (L 0 ) ( 2 ) dt t0 L 31 General solution The solution is the sum of final current If =Is and the nature response iL,nature (t): iL() tf I L i, nature( ), t where the three types of nature responses were elucidated in Section 8.2: s1 t s2 t I f A 1 e 2, A if e 0 , t iL()I t ef B1cosd tsin2 Bd , if t 0 , t I ef D1 t, 2 Dif 0 .
Load more

Recommended publications
  • LABORATORY 3: Transient Circuits, RC, RL Step Responses, 2Nd Order Circuits
    Alpha Laboratories ECSE-2010 LABORATORY 3: Transient circuits, RC, RL step responses, 2nd Order Circuits Note: If your partner is no longer in the class, please talk to the instructor. Material covered: RC circuits Integrators Differentiators 1st order RC, RL Circuits 2nd order RLC series, parallel circuits Thevenin circuits Part A: Transient Circuits RC Time constants: A time constant is the time it takes a circuit characteristic (Voltage for example) to change from one state to another state. In a simple RC circuit where the resistor and capacitor are in series, the RC time constant is defined as the time it takes the voltage across a capacitor to reach 63.2% of its final value when charging (or 36.8% of its initial value when discharging). It is assume a step function (Heavyside function) is applied as the source. The time constant is defined by the equation τ = RC where τ is the time constant in seconds R is the resistance in Ohms C is the capacitance in Farads The following figure illustrates the time constant for a square pulse when the capacitor is charging and discharging during the appropriate parts of the input signal. You will see a similar plot in the lab. Note the charge (63.2%) and discharge voltages (36.8%) after one time constant, respectively. Written by J. Braunstein Modified by S. Sawyer Spring 2020: 1/26/2020 Rensselaer Polytechnic Institute Troy, New York, USA 1 Alpha Laboratories ECSE-2010 Written by J. Braunstein Modified by S. Sawyer Spring 2020: 1/26/2020 Rensselaer Polytechnic Institute Troy, New York, USA 2 Alpha Laboratories ECSE-2010 Discovery Board: For most of the remaining class, you will want to compare input and output voltage time varying signals.
    [Show full text]
  • Experiment 12: AC Circuits - RLC Circuit
    Experiment 12: AC Circuits - RLC Circuit Introduction An inductor (L) is an important component of circuits, on the same level as resistors (R) and capacitors (C). The inductor is based on the principle of inductance - that moving charges create a magnetic field (the reverse is also true - a moving magnetic field creates an electric field). Inductors can be used to produce a desired magnetic field and store energy in its magnetic field, similar to capacitors being used to produce electric fields and storing energy in their electric field. At its simplest level, an inductor consists of a coil of wire in a circuit. The circuit symbol for an inductor is shown in Figure 1a. So far we observed that in an RC circuit the charge, current, and potential difference grew and decayed exponentially described by a time constant τ. If an inductor and a capacitor are connected in series in a circuit, the charge, current and potential difference do not grow/decay exponentially, but instead oscillate sinusoidally. In an ideal setting (no internal resistance) these oscillations will continue indefinitely with a period (T) and an angular frequency ! given by 1 ! = p (1) LC This is referred to as the circuit's natural angular frequency. A circuit containing a resistor, a capacitor, and an inductor is called an RLC circuit (or LCR), as shown in Figure 1b. With a resistor present, the total electromagnetic energy is no longer constant since energy is lost via Joule heating in the resistor. The oscillations of charge, current and potential are now continuously decreasing with amplitude.
    [Show full text]
  • ELECTRICAL CIRCUIT ANALYSIS Lecture Notes
    ELECTRICAL CIRCUIT ANALYSIS Lecture Notes (2020-21) Prepared By S.RAKESH Assistant Professor, Department of EEE Department of Electrical & Electronics Engineering Malla Reddy College of Engineering & Technology Maisammaguda, Dhullapally, Secunderabad-500100 B.Tech (EEE) R-18 MALLA REDDY COLLEGE OF ENGINEERING AND TECHNOLOGY II Year B.Tech EEE-I Sem L T/P/D C 3 -/-/- 3 (R18A0206) ELECTRICAL CIRCUIT ANALYSIS COURSE OBJECTIVES: This course introduces the analysis of transients in electrical systems, to understand three phase circuits, to evaluate network parameters of given electrical network, to draw the locus diagrams and to know about the networkfunctions To prepare the students to have a basic knowledge in the analysis of ElectricNetworks UNIT-I D.C TRANSIENT ANALYSIS: Transient response of R-L, R-C, R-L-C circuits (Series and parallel combinations) for D.C. excitations, Initial conditions, Solution using differential equation and Laplace transform method. UNIT - II A.C TRANSIENT ANALYSIS: Transient response of R-L, R-C, R-L-C Series circuits for sinusoidal excitations, Initial conditions, Solution using differential equation and Laplace transform method. UNIT - III THREE PHASE CIRCUITS: Phase sequence, Star and delta connection, Relation between line and phase voltages and currents in balanced systems, Analysis of balanced and Unbalanced three phase circuits UNIT – IV LOCUS DIAGRAMS & RESONANCE: Series and Parallel combination of R-L, R-C and R-L-C circuits with variation of various parameters.Resonance for series and parallel circuits, concept of band width and Q factor. UNIT - V NETWORK PARAMETERS:Two port network parameters – Z,Y, ABCD and hybrid parameters.Condition for reciprocity and symmetry.Conversion of one parameter to other, Interconnection of Two port networks in series, parallel and cascaded configuration and image parameters.
    [Show full text]
  • Lecture 4: RLC Circuits and Resonant Circuits
    Lecture 4: R-L-C Circuits and Resonant Circuits RLC series circuit: ● What's VR? ◆ Simplest way to solve for V is to use voltage divider equation in complex notation: V R X L X C V = in R R + XC + XL L C R Vin R = Vin = V0 cosω t 1 R + + jωL jωC ◆ Using complex notation for the apply voltage V = V cosωt = Real(V e jωt ): j t in 0 0 V e ω R V = 0 R $ 1 ' € R + j& ωL − ) % ωC ( ■ We are interested in the both the magnitude of VR and its phase with respect to Vin. ■ First the magnitude: jωt V0e R € V = R $ 1 ' R + j& ωL − ) % ωC ( V R = 0 2 2 $ 1 ' R +& ωL − ) % ωC ( K.K. Gan L4: RLC and Resonance Circuits 1 € ■ The phase of VR with respect to Vin can be found by writing VR in purely polar notation. ❑ For the denominator we have: 0 * 1 -4 2 ωL − $ 1 ' 2 $ 1 ' 2 1, /2 R + j& ωL − ) = R +& ωL − ) exp1 j tan− ωC 5 % C ( % C( , R / ω ω 2 , /2 3 + .6 ❑ Define the phase angle φ : Imaginary X tanφ = Real X € 1 ωL − = ωC R ❑ We can now write for VR in complex form: V R e jωt V = o R 2 € jφ 2 % 1 ( e R +' ωL − * Depending on L, C, and ω, the phase angle can be & ωC) positive or negative! In this example, if ωL > 1/ωC, j(ωt−φ) then VR(t) lags Vin(t). = VR e ■ Finally, we can write down the solution for V by taking the real part of the above equation: j(ωt−φ) V R e V R cos(ωt −φ) V = Real 0 = 0 R 2 2 € 2 % 1 ( 2 % 1 ( R +' ωL − * R +' ωL − * & ωC ) & ωC ) K.K.
    [Show full text]
  • Lecture 14 - AC Circuits, Resonance Y&F Chapter 31, Sec
    Physics 121 - Electricity and Magnetism Lecture 14 - AC Circuits, Resonance Y&F Chapter 31, Sec. 3 - 8 • The Series RLC Circuit. Amplitude and Phase Relations • Phasor Diagrams for Voltage and Current • Impedance and Phasors for Impedance • Resonance • Power in AC Circuits, Power Factor • Examples • Transformers • Summaries Copyright R. Janow – Fall 2013 Current & voltage phases in pure R, C, and L circuits Current is the same everywhere in a single branch (including phase) Phases of voltages in elements are referenced to the current phasor • Apply sinusoidal voltage E (t) = EmCos(wDt) • For pure R, L, or C loads, phase angles are 0, +p/2, -p/2 • Reactance” means ratio of peak voltage to peak current (generalized resistances). VR& iR in phase VC lags iC by p/2 VL leads iL by p/2 Resistance Capacitive Reactance Inductive Reactance 1 V /i R Vmax /iC C Vmax /iL L wDL max R wDC Copyright R. Janow – Fall 2013 The impedance is the ratio of peak EMF to peak current peak applied voltage Em Z [Z] ohms peak current that flows im 2 2 2 Magnitude of Em: Em VR (VL VC) 1 Reactances: L wDL C wDC L VL /iL C VC /iC R VR /iR im iR,max iL,max iC,max For series LRC circuit, divide Em by peak current 2 2 1/2 Applies to a single Magnitude of Z: Z [ R (L C) ] branch with L, C, R VL VC L C Phase angle F: tan(F) see diagram VR R F measures the power absorbed by the circuit: P Em im Em im cos(F) • R ~ 0 tiny losses, no power absorbed im normal to Em F ~ +/- p/2 • XL=XC im parallel to Em F 0 Z=R maximum currentCopyright (resonance) R.
    [Show full text]
  • AC Power • Resonant Circuits • Phasors (2-Dim Vectors, Amplitude and Phase) What Is Reactance ? You Can Think of It As a Frequency-Dependent Resistance
    Physics-272 Lecture 20 • AC Power • Resonant Circuits • Phasors (2-dim vectors, amplitude and phase) What is reactance ? You can think of it as a frequency-dependent resistance. 1 For high ω, χ ~0 X = C C ωC - Capacitor looks like a wire (“short”) For low ω, χC∞ - Capacitor looks like a break For low ω, χL~0 - Inductor looks like a wire (“short”) XL = ω L For high ω, χL∞ - Inductor looks like a break (inductors resist change in current) ("XR "= R ) An RL circuit is driven by an AC generator as shown in the figure. For what driving frequency ω of the generator, will the current through the resistor be largest a) ω large b) ω small c) independent of driving freq. The current amplitude is inversely proportional to the frequency of the ω generator. (X L= L) Alternating Currents: LRC circuit Figure (b) has XL>X C and (c) has XL<X C . Using Phasors, we can construct the phasor diagram for an LRC Circuit. This is similar to 2-D vector addition. We add the phasors of the resistor, the inductor, and the capacitor. The inductor phasor is +90 and the capacitor phasor is -90 relative to the resistor phasor. Adding the three phasors vectorially, yields the voltage sum of the resistor, inductor, and capacitor, which must be the same as the voltage of the AC source. Kirchoff’s voltage law holds for AC circuits. Also V R and I are in phase. Phasors R ε ω Problem : Given Vdrive = m sin( t), C L find VR, VL, VC, IR, IL, IC ε ∼ Strategy : We will use Kirchhoff’s voltage law that the (phasor) sum of the voltages VR, VC, and VL must equal Vdrive .
    [Show full text]
  • Chapter 14 Frequency Response
    CHAPTER 14 FREQUENCYRESPONSE One machine can do the work of fifty ordinary men. No machine can do the work of one extraordinary man. — Elbert G. Hubbard Enhancing Your Career Career in Control Systems Control systems are another area of electrical engineering where circuit analysis is used. A control system is designed to regulate the behavior of one or more variables in some desired manner. Control systems play major roles in our everyday life. Household appliances such as heating and air-conditioning systems, switch-controlled thermostats, washers and dryers, cruise controllers in automobiles, elevators, traffic lights, manu- facturing plants, navigation systems—all utilize control sys- tems. In the aerospace field, precision guidance of space probes, the wide range of operational modes of the space shuttle, and the ability to maneuver space vehicles remotely from earth all require knowledge of control systems. In the manufacturing sector, repetitive production line opera- tions are increasingly performed by robots, which are pro- grammable control systems designed to operate for many hours without fatigue. Control engineering integrates circuit theory and communication theory. It is not limited to any specific engi- neering discipline but may involve environmental, chemical, aeronautical, mechanical, civil, and electrical engineering. For example, a typical task for a control system engineer might be to design a speed regulator for a disk drive head. A thorough understanding of control systems tech- niques is essential to the electrical engineer and is of great value for designing control systems to perform the desired task. A welding robot. (Courtesy of Shela Terry/Science Photo Library.) 583 584 PART 2 AC Circuits 14.1 INTRODUCTION In our sinusoidal circuit analysis, we have learned how to find voltages and currents in a circuit with a constant frequency source.
    [Show full text]
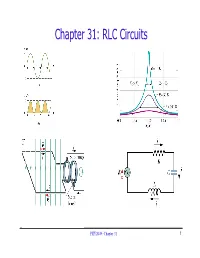
  • Chapter 31: RLC Circuits
    Chapter 31: RLC Circuits PHY2049: Chapter 31 1 Topics ÎLC Oscillations Conservation of energy ÎDamped oscillations in RLC circuits Energy loss ÎAC current RMS quantities ÎForced oscillations Resistance, reactance, impedance Phase shift Resonant frequency Power ÎTransformers Impedance matching PHY2049: Chapter 31 2 LC Oscillations ÎWork out equation for LC circuit (loop rule) qdi C −−L =0 L Cdt ÎRewrite using i = dq/dt dq22 q dq 1 Lq+=⇒00 +ω 2 = ω = dt22C dt LC ω (angular frequency) has dimensions of 1/t ÎIdentical to equation of mass on spring dx22 dx k mkx+=⇒00 +ω 2 x = ω = dt22 dt m PHY2049: Chapter 31 3 LC Oscillations (2) ÎSolution is same as mass on spring ⇒ oscillations k qq=+max cos()ω tθ ω = m qmax is the maximum charge on capacitor θ is an unknown phase (depends on initial conditions) ÎCalculate current: i = dq/dt iq=−ω maxsin(ωθ t +) =− i max sin( ωθ t + ) ÎThus both charge and current oscillate Angular frequency ω, frequency f = ω/2π Period: T = 2π/ω PHY2049: Chapter 31 4 Plot Charge and Current vs t ω =12T = π qt( ) it( ) PHY2049: Chapter 31 5 Energy Oscillations ÎTotal energy in circuit is conserved. Let’s see why di q L +=0 Equation of LC circuit dt C di q dq Li+=0 Multiply by i = dq/dt dt C dt 2 Ld221 d dx dx iq+=0 Use = 2x 22dt( ) C dt ( ) dt dt 2 2 dq⎛⎞ 112 q 11Li2 +=0 Li +=const ⎜⎟22 22C dt⎝⎠ C UL + UC = const PHY2049: Chapter 31 6 Oscillation of Energies ÎEnergies can be written as (using ω2 = 1/LC) 2 2 q q 2 Ut==max cos ()ω +θ C 22CC 2 2222q 2 ULiLq==11ω sin()ωθ t +=max sin () ωθ t + L 22max 2C q2 ÎConservation
    [Show full text]
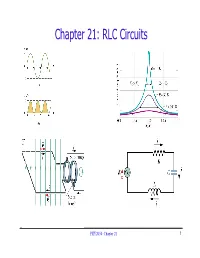
  • Chapter 21: RLC Circuits
    Chapter 21: RLC Circuits PHY2054: Chapter 21 1 Voltage and Current in RLC Circuits ÎAC emf source: “driving frequency” f ε = εωm sin t ω = 2π f ÎIf circuit contains only R + emf source, current is simple ε ε iI==sin()ω tI =m () current amplitude R mmR ÎIf L and/or C present, current is not in phase with emf ε iI=−=sin()ωφ t I m mmZ ÎZ, φ shown later PHY2054: Chapter 21 2 AC Source and Resistor Only ÎDriving voltage is ε = εωm sin t i ÎRelation of current and voltage iR= ε / ε ~ R ε iI==sinω tI m mmR Current is in phase with voltage (φ = 0) PHY2054: Chapter 21 3 AC Source and Capacitor Only q ÎVoltage is vt==ε sinω CmC ÎDifferentiate to find current i qC= εm sinω t idqdtCV==/cosω C ω t ε ~ C ÎRewrite using phase (check this!) iCVt=+°ω C sin()ω 90 ÎRelation of current and voltage εm iI=+°=mmsin()ω t 90 I ( XC =1/ωC) XC ΓCapacitive reactance”: XCC =1/ω Current “leads” voltage by 90° PHY2054: Chapter 21 4 AC Source and Inductor Only ÎVoltage is vLm== Ldi/sin dtε ω t ÎIntegrate di/dt to find current: i di//sin dt= ()εm Lω t iLt=−()εm /cosωω ε ~ L ÎRewrite using phase (check this!) iLt=−°()εm /sin90ωω( ) ÎRelation of current and voltage εm iI=−°=mmsin()ω t 90 I ( XLL = ω ) X L ΓInductive reactance”: XLL = ω Current “lags” voltage by 90° PHY2054: Chapter 21 5 General Solution for RLC Circuit ÎWe assume steady state solution of form iI= m sin(ω t−φ ) Im is current amplitude φ is phase by which current “lags” the driving EMF Must determine Im and φ ÎPlug in solution: differentiate & integrate sin(ωt-φ) iI=−m sin()ω tφ di Substitute di q
    [Show full text]
  • MAGNETIC FIELD SHIELDING by METAMATERIALS Mustafa Boyvat
    Progress In Electromagnetics Research, Vol. 136, 647{664, 2013 MAGNETIC FIELD SHIELDING BY METAMATERIALS Mustafa Boyvat* and Christian Hafner Department of Information Technology and Electrical Engineering, ETH Zurich, Gloriastrasse 35, Zurich 8092, Switzerland Abstract|Magnetic ¯eld shielding at low frequencies is a problem of high importance that is known for a long time. Metamaterials, which are known from fancy applications such as the so-called perfect lens and cloaking, also o®er a new way to create e±cient magnetic shielding by means of anisotropic metamaterials with low permeability in one direction. Such metamaterials can be constructed by assembling arrays of relatively simple LC circuits. In this paper, we analyze di®erent metamaterials and show how they may be designed. We show that typical resistive losses in the coils and capacitors of the LC circuits reduce the shielding quality. Then, we consider the possibility of active electronic loss compensation and discuss the drawbacks of this concept. After this, we propose a purely passive way that bene¯ts from the inhomogeneity of the magnetic ¯eld to be shielded. Finally, we present experimental results, which show the performance of metamaterial shields. 1. INTRODUCTION Metamaterials are materials which can provide unusual or extraordi- narily strong electromagnetic properties, which cannot be found in natural materials [1, 2]. In 2000, Pendry theoretically showed that one can make a perfect lens, which is not limited by di®raction limit, by using metamaterials with negative permittivity and negative perme- ability [3]. After this, metamaterials attracted much attention and also experimental work has been done to demonstrate negative refrac- tion and superlensing e®ects [4{9].
    [Show full text]
  • Frequency Responses in RLC Circuits
    Frequency Responses in RLC Circuits Dalton Eaton and Uladzimir Kasacheuski Indiana University - Purdue University Indianapolis (Dated: February 11, 2017) The bandpass filter and the notch filter, the 'inverse' of the bandpass filter, are circuits for valued for their utility in attenuating specific frequencies of a signal. In this paper we create the two filters, in the forms of resistor-inductor-capacitor (RLC) circuits, and examine both circuits from experimental and theoretical views. The filters are shown to accurately attenuated selective frequencies based on chosen component values. The results demonstrate that these filters are highly predictable: the theoretical and experimental values match very well even in non-ideal circumstances. I. INTRODUCTION AND BACKGROUND X = j!L (1) Filters are commonly used circuits for the selective L attenuation of specific frequencies. A band-pass filter is designed to attenuate all frequencies except those lying within a certain band. A notch filter, or band-reject XC = −1=(j!C) (2) filter, is the 'inverse' of the band pass filter; all frequen- cies are passed in a notch filter except for those lying Equations 1 and 2 determine the impedance of the in- with a certain range, the 'notch'. An RLC circuit is a ductor and capacitor, the analogue of resistance for the simple yet effective method for the construction of both transient components of the two. At a specific value of ! of these common and powerful filters. designated by !o, the two terms will be equal and oppo- site. Using Ohm's law, the voltage found on the capaci- tor and inductor will sum to zero and thus Vsource will be equivalent to the voltage found across the resistor.
    [Show full text]
  • Chapter 32 Lecture
    3/25/2019 PHYSICS FOR SCIENTISTS AND ENGINEERS A STRATEGIC APPROACH 4/ E Chapter 32 Lecture RANDALL D. KNIGHT Chapter 32 AC Circuits IN THIS CHAPTER, you will learn about and analyze AC circuits. © 2017 Pearson Education, Inc. Slide 32-2 Chapter 32 Preview © 2017 Pearson Education, Inc. Slide 32-3 1 3/25/2019 Chapter 32 Preview © 2017 Pearson Education, Inc. Slide 32-4 Chapter 32 Preview © 2017 Pearson Education, Inc. Slide 32-5 Chapter 32 Preview © 2017 Pearson Education, Inc. Slide 32-6 2 3/25/2019 Chapter 32 Preview © 2017 Pearson Education, Inc. Slide 32-7 Chapter 32 Reading Questions © 2017 Pearson Education, Inc. Slide 32-8 Reading Question 32.1 In Chapter 32, “AC” stands for A. Air cooling. B. Air conditioning. C. All current. D. Alternating current. E. Analog current. © 2017 Pearson Education, Inc. Slide 32-9 3 3/25/2019 Reading Question 32.1 In Chapter 32, “AC” stands for A. Air cooling. B. Air conditioning. C. All current. D. Alternating current. E. Analog current. © 2017 Pearson Education, Inc. Slide 32-10 Reading Question 32.2 The analysis of AC circuits uses a rotating vector called a A. Rotor. B. Wiggler. C. Phasor. D. Motor. E. Variator. © 2017 Pearson Education, Inc. Slide 32-11 Reading Question 32.2 The analysis of AC circuits uses a rotating vector called a A. Rotor. B. Wiggler. C. Phasor. D. Motor. E. Variator. © 2017 Pearson Education, Inc. Slide 32-12 4 3/25/2019 Reading Question 32.3 In a capacitor, the peak current and peak voltage are related by the A.
    [Show full text]