Selection of Open Pit Excavating Equipment - a Systems Approach
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Stannaries
THE STANNARIES A STUDY OF THE MEDIEVAL TIN MINERS OF CORNWALL AND DEVON G. R. LEWIS First published 1908 PREFACE THEfollowing monograph, the outcome of a thesis for an under- graduate course at Harvard University, is the result of three years' investigation, one in this country and two in England, - for the most part in London, where nearly all the documentary material relating to the subject is to be found. For facilitating with ready courtesy my access to this material I am greatly indebted to the officials of the 0 GEORGE RANDALL LEWIS British Museum, the Public Record Office, and the Duchy of Corn- wall Office. I desire also to acknowledge gratefully the assistance of Dr. G. W. Prothero, Mr. Hubert Hall, and Mr. George Unwin. My thanks are especially due to Professor Edwin F. Gay of Harvard University, under whose supervision my work has been done. HOUGHTON,M~CHIGAN, November, 1907. CONTENTS INTRODUCTION purpose of the essay. Reasons for choice of subject. Sources of informa- tion. Plan of treatment . xiii CHAPTER I Nature of tin ore. Stream tinning in early times. Early methods of searching for ore. Forms assumed by the primitive mines. Drainage and other features of medizval mine economy. Preparation of the ore. Carew's description of the dressing of tin ore. Early smelting furnaces. Advances in mining and smelt- ing in the latter half of the seventeenth century. Preparation of the ore. Use of the steam engine for draining mines. Introduction of blasting. Pit coal smelting. General advance in ore dressing in the eighteenth century. Other improvements. -

Cc21-102 Addendum #2 Bear Valley Road
Kris J. Kofoed From: Sanchez, Jason L <[email protected]> Sent: Monday, June 14, 2021 1:27 PM To: Jamie Formico Cc: Kris J. Kofoed; Townlian, Cheryl L Subject: FW: City of Victorville- Bear Valley out to Bid Attachments: C&M Agreement.pdf; Pages from C&M Agreement (Executed).pdf; Pages from IIPlans.pdf CAUTION: This email originated from outside of the organization. Do not click links or open attachments unless you recognize the sender and know the content is safe. Hi Jamie: Per our recent conversation, the shoring system is 12 feet from the face to centerline of track. Even though this is less than the 15’ feet called out in C&M Agreement, this reduced clearance is only temporary (no more than 6 hours) and not an issue. During the construction of the shoring wall, a work window will be established to eliminate train traffic on the adjacent track for that short duration. Once installed, the shoring system will be at the same elevation or lower than the top of rail, making the 12 feet clearance moot. Any questions, please ask. Thank you, Jason L. Sanchez BNSF Railway Manager Engineering 740 E. Carnegie Drive San Bernardino, CA 92408 909-386-4470 [email protected] From: Jamie Formico <[email protected]> Sent: Wednesday, May 19, 2021 9:32 AM To: Sanchez, Jason L <[email protected]>; Townlian, Cheryl L <[email protected]>; Kris J. Kofoed <[email protected]> Subject: City of Victorville‐ Bear Valley out to Bid *** This email includes an ATTACHMENT from outside of BNSF and could contain malicious links. -

~ Coal Mining in Canada: a Historical and Comparative Overview
~ Coal Mining in Canada: A Historical and Comparative Overview Delphin A. Muise Robert G. McIntosh Transformation Series Collection Transformation "Transformation," an occasional paper series pub- La collection Transformation, publication en st~~rie du lished by the Collection and Research Branch of the Musee national des sciences et de la technologic parais- National Museum of Science and Technology, is intended sant irregulierement, a pour but de faire connaitre, le to make current research available as quickly and inex- plus vite possible et au moindre cout, les recherches en pensively as possible. The series presents original cours dans certains secteurs. Elle prend la forme de research on science and technology history and issues monographies ou de recueils de courtes etudes accep- in Canada through refereed monographs or collections tes par un comite d'experts et s'alignant sur le thenne cen- of shorter studies, consistent with the Corporate frame- tral de la Societe, v La transformation du CanadaLo . Elle work, "The Transformation of Canada," and curatorial presente les travaux de recherche originaux en histoire subject priorities in agricultural and forestry, communi- des sciences et de la technologic au Canada et, ques- cations and space, transportation, industry, physical tions connexes realises en fonction des priorites de la sciences and energy. Division de la conservation, dans les secteurs de: l'agri- The Transformation series provides access to research culture et des forets, des communications et de 1'cspace, undertaken by staff curators and researchers for develop- des transports, de 1'industrie, des sciences physiques ment of collections, exhibits and programs. Submissions et de 1'energie . -
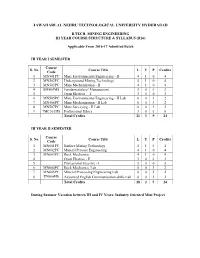
Iii Year Course Structure & Syllabus (R16)
JAWAHARLAL NEHRU TECHNOLOGICAL UNIVERSITY HYDERABAD B.TECH. MINING ENGINEERING III YEAR COURSE STRUCTURE & SYLLABUS (R16) Applicable From 2016-17 Admitted Batch III YEAR I SEMESTER Course S. No Course Title L T P Credits Code 1 MN501PC Mine Environmental Engineering - II 4 1 0 4 2 MN502PC Underground Mining Technology 4 1 0 4 3 MN503PC Mine Mechanization - II 4 1 0 4 4 SM504MS Fundamentals of Management 3 0 0 3 5 Open Elective – I 3 0 0 3 6 MN505PC Mine Environmental Engineering - II Lab 0 0 3 2 7 MN506PC Mine Mechanization - II Lab 0 0 3 2 8 MN507PC Mine Surveying - II Lab 0 0 3 2 9 *MC500HS Professional Ethics 3 0 0 0 Total Credits 21 3 9 24 III YEAR II SEMESTER Course S. No Course Title L T P Credits Code 1 MN601PC Surface Mining Technology 4 1 0 4 2 MN602PC Mineral Process Engineering 4 1 0 4 3 MN603PC Rock Mechanics 4 1 0 4 4 Open Elective - II 3 0 0 3 5 Professional Elective - I 3 0 0 3 6 MN604PC Rock Mechanics Lab 0 0 3 2 7 MN605PC Mineral Processing Engineering Lab 0 0 3 2 8 EN606HS Advanced English Communication skills Lab 0 0 3 2 Total Credits 18 3 9 24 During Summer Vacation between III and IV Years: Industry Oriented Mini Project Professional Elective - I MN611PE Mine Systems Engineering MN612PE Remote Sensing and GIS in Mining MN613PE Dimensional Stone Technology MN614PE Mineral Exploration *Open Elective subjects’ syllabus is provided in a separate document. -

ABB's Long History of Making Mining Operations More Efficient
ABB’s long history of making mining operations more efficient Innovative technologies have improved productivity for mining since the 1890s ABB’s comprehensive automation and power delivery at Boliden’s Aitik copper concentrator plant is the latest chapter in the company’s rich history of improving the operations of all types of mines and ore processing plants. The company has provided solutions that make mining operations more efficient, productive and safe for almost 120 years, since delivering the first drives and controls for a mine hoist at the Kolningsberget iron mine in Norberg, Sweden, in 1891. Drives and controls help mine hoists operate more efficiently and consistently as they haul tons of ore from lower levels of a mine to the surface. Over the years, ABB has made other breakthroughs in mine hoist technology including hydraulic disc brakes, controlled braking and Rope Oscillation Control, all of which have made mine hoists more reliable and safer to operate. ABB has delivered more than 600 new hoists and modernized hundreds of existing plants. A mine hoist delivered around 1930 by ASEA, a predecessor of ABB, to the Zinkgruvan zinc mine in Sweden is still in operation today. Pioneer of gearless mill drives ABB pioneered the development of gearless mill drive (GMD) systems, which are giant motor and drive systems that power ore-crushing mills. They are more reliable and energy efficient than traditional mill drive systems, and increase mill productivity. ABB delivered the world’s first gearless machine drive to Lafarge Cement in France in 1969. The 6.4 megawatt (MW) equipment is still operating today. -

Department of the Interior
DEPARTMENTOF THE INTERIOR UNITED STATES BUREAU OF MINES JOHNW. FINCH*DIRCC~OFI INFORMATION CIRCULAR - PLACER MINING IN THE WESTERN UNlTED STATES - - PART Ill. DREDGING AND OTHER FORMS OF MECHANICAL. HANDLING OF GRAVEL, AND DRIFT MINING 1 I . .C. 6788. February 1935 Part I11 . .Dredeing and Other Forms of Mechanical Handling of Eravel . and Drift Miniqg CONTENTS Introduction ....................................................................................:..................... Acknowledgments ..................................................................:................................. Excavating by teams or power equipment ...................................................... General statement...................................................................................... Team or traotors...................................................................................... Teams .................................................................................................... Tractors.............................................................................................. Scrapers and hoists.................................................................................. Drag scrapers...... : ............................................................................. Slaokline on oablewags .................................................................. Power shovels and draglines.................................................................. Stationary washing plants........................................................... -

Methods and Results of Strip-Mine Reclamation in Germany1
No. 2 GEOLOGY OF COAL OVERBURDEN 75 METHODS AND RESULTS OF STRIP-MINE RECLAMATION IN GERMANY1 WILHELM KNABE2 Federal Research Organization for Forestry and Forest Products, Reinbek Hamburg, Germany All over the world industry is growing rapidly. This growth includes a great increase of surface mining or strip mining, as you call it. In the last 20 years, it has increased much more than underground mining, which, in some of the old industrial countries, is decreasing substantially. A number of factors have con- tributed to this trend; these include the development of heavy equipment, lower costs, more complete recovery of the coal, and smaller labor requirements. The American strip mines for bituminous coal and the German opencast mines for brown coal (also called lignite) are among the most important examples. This report will present the facts and trends of mining and reclamation in Germany only; it will not at this time make any direct comparison with the situation in Ohio. As you will see, there are very different conditions and solutions, but also very similar trends and problems in the two countries. Let me take three examples. (1) In both countries the mining industry is forced to go deeper and deeper into the earth, because many of the most favor- 1Presented at the Strip-mine Symposium held at the Ohio Agricultural Experiment Station on August 13-14, 1962. 2Summer 1962: Post-Doctoral Fellow, Ohio Agricultural Experiment Station, Wooster, Ohio. This opportunity was made possible by a Fulbright Travel Grant-Senior program of U. S. Educational Commission, Bad Godesberg, Germany. THE OHIO JOURNAL OF SCIENCE 64(2): 75, March, 1964. -

Dragline Maintenance Engineering
University of Southern Queensland Faculty of Engineering and Surveying Dragline Maintenance Engineering A dissertation submitted by Bruce Thomas Jones in fulfilment of the requirements of Courses ENG4111 and 4112 Research Project towards the degree of Bachelor of Engineering (Mechanical) Submitted November, 2007 1 ABSTRACT This research project ‘Dragline Maintenance Engineering’ explores the maintenance strategies for large walking draglines over the past 30 years in the Australian coal industry. Many draglines built since the 1970’s are still original in configuration and utilize original component technology. ie electrical drives, gear configurations. However, there have been many innovative enhancements, configuration changes and upgrading of components The objective is to critically analyze the maintenance strategies, and to determine whether these strategies are still supportive of optimizing the availability and reliability of the draglines. The maintenance strategies associated with dragline maintenance vary, dependent on fleet size and mine conditions; they are aligned with the Risk Based Model. The effectiveness of the maintenance strategy implemented with dragline maintenance is highly dependent on the initial effort demonstrated at the commencement of planning for the mining operation. Mine size, productivity requirements, machinery configuration and economic factors drive the maintenance strategies associated with Dragline Maintenance Engineering. 2 University of Southern Queensland Faculty of Engineering and Surveying ENG4111 -

Structural Health Monitoring of Walking Dragline Excavator Using Acoustic Emission
applied sciences Article Structural Health Monitoring of Walking Dragline Excavator Using Acoustic Emission Vera Barat 1,2, Artem Marchenkov 1,* , Dmitry Kritskiy 3, Vladimir Bardakov 1,2, Marina Karpova 1, Mikhail Kuznetsov 1, Anastasia Zaprudnova 1, Sergey Ushanov 1,2 and Sergey Elizarov 2 1 Moscow Power Engineering Institute, 14, Krasnokazarmennaya Str., 111250 Moscow, Russia; [email protected] (V.B.); [email protected] (V.B.); [email protected] (M.K.); [email protected] (M.K.); [email protected] (A.Z.); [email protected] (S.U.) 2 LLC “Interunis-IT”, 20b, Entuziastov Sh., 111024 Moscow, Russia; [email protected] 3 JSC “SUEK”: 20b, Lenin Str., 660049 Krasnoyarsk, Russia; [email protected] * Correspondence: [email protected] Abstract: The article is devoted to the organization of the structural health monitoring of a walking dragline excavator using the acoustic emission (AE) method. Since the dragline excavator under study is a large and noisy industrial facility, preliminary prospecting researches were carried out to conduct effective control by the AE method, including the study of AE sources, AE waveguide, and noise parameters analysis. In addition, AE filtering methods were improved. It is shown that application of the developed filtering algorithms allows to detect AE impulses from cracks and defects against a background noise exceeding the useful signal in amplitude and intensity. Using the proposed solutions in the monitoring of a real dragline excavator during its operation made it possible to identify a crack in one of its elements (weld joint in a dragline back leg). Citation: Barat, V.; Marchenkov, A.; Kritskiy, D.; Bardakov, V.; Karpova, M.; Kuznetsov, M.; Zaprudnova, A.; Keywords: acoustic emission; structure health monitoring; walking excavator; AE impulse detection Ushanov, S.; Elizarov, S. -

King Coal Historic Mine Byway
King Coal Historic Mine Byway Interpretive Plan “Wyodak coal mine near Gillette, WY, Val Kuska July – Aug 1930” (Wyoming State Archives, Kuska Collection, File 661-680) T O X E Y • M C M I L L A N D E S I G N A S S O C I A T E S • L L C 218 Washington Street, San Antonio, TX 78204 • O: 210-225-7066 • C: 817-368-2750 http://www.tmdaexhibits.com • [email protected] Interpretive Plan 1 “Coal? Wyoming has enough with which to run the forges of Vulcan, weld every tie that binds, drive every wheel, change the North Pole into a tropical region or smelt all Hell.” —Fenimore Chatterton, Wyoming Secretary of State, 1902 This interpretive plan was developed by Toxey/McMillan Design Associates between 2014 and 2017 under contract from the Wyoming State Historic Preservation Office. The project scope was revised in 2016 at the request of the Wyoming SHPO and local project participants. This document reflects a historical perspective on the Campbell County Coal Industry rather than current events and economic conditions. Interpretive Plan 2 Table of Contents Introduction to the Project p. 5 Interpretive Significance p. 6 Project Goal p. 9 Intent of the Interpretive Plan p. 10 Methodology and Development Process p. 10 Audience Profile p. 11 Visitor Needs p. 18 Project Objectives p. 19 Underlying Theme p. 21 Name Considerations p. 21 Interpretation Topics and Subtopics p. 22 Storyline Development p. 24 Route Recommendation p. 118 Media Plan and Recommendations p. 130 Cost Estimates p. 135 References p. -

<Pea~ Cvistrict ~Iries Chistorical C-Societycltd
<pea~ CVistrict ~iries CHistorical C-SocietyCLtd. NEWSLETTER No 96 OCTOBER 2000 SUMMARY OF DATES FOR YOUR DIARY 22 October U/ground meet - Rochdale Page 2 19 November Ecton Mines Page 3 25 November AGM and Anual Dinner Page 1 22-23 September 2000 NAMHO Field Meet Pagell TO ALL MEMBERS MrN Potter+ ~otice is hereby given that the Twenty Sixth Annual Mr J R Thorpe*(Acting Hon secretary) General Meeting of the Peak District Mines Historical Those whose names are marked (*) are retiring as Society Ltd will be held at 6.00pm on Saturday required by the Articles of Association and are eligible for 25 November 2000 at the Peak District Mining Museum, re-election. Those whose names are marked (+) are Grand Pavilion, Matlock Bath, Derbyshire. retiring and are not eligible for re-election. The Agenda will be distributed at the start of the Fully paid up members of the Society, who are aged meeting. 18 years and over, are invited to nominate Members of the By Order Society (who themselves are fully paid up and who have J Thorpe consented to the nomination) for the vacant positions on Hon Secretary the Committee. Nominations are required for the position of: THE COMPANIES ACT 1985 As required under Article 24 of the Articles of Chairman Association of the Company, the following Directors will Deputy Chairman retire at the Annual General Meeting: Hon Secretary 1. The Hon Secretary (acting) Hon Treasurer 2. The Chairman Hon Recorder 3. The Deputy Chairman Hon Editor 4. The Hon Treasurer Two Ordinary Members 5. The Hon Editor 6. -

Application of Mcda in Selection of Different Mining Methods and Solutions
Advances in Science and Technology Research Journal Volume 12, Issue 1, March 2018, pages 171–180 Research Article DOI: 10.12913/22998624/85804 APPLICATION OF MCDA IN SELECTION OF DIFFERENT MINING METHODS AND SOLUTIONS Dejan Stevanović1, Milena Lekić1, Daniel Kržanović2, Ivica Ristović1 1 Faculty of Mining and Geology, Djusina 7, 11000 Belgrade, Serbia, e-mail: [email protected]; [email protected]; [email protected] 2 Mining and Metallurgy Institute Bor, Zeleni bulevar 35 19210 Bor, Serbia, e-mail: [email protected] Received: 2018.01.15 ABSTRACT Accepted: 2018.02.01 As mine planning is one of the most complicated steps, which depends on a lot Published: 2018.03.01 of factors as geology, economy etc., consequently, the decision-making process is difficult, due to the existence of a lot of factors for choosing the optimal mining system. In this paper, the method and the result of Analytical Hierarchical Process is presented, shown on a case study – Open pit Drmno, as one of the largest lignite mines in Serbia. The analysis included 6 criteria and two alternatives were applied as Variant 1 and Variant 2. The results show that the suitable mining system for this case study – open pit Drmno is Variant 2. Keywords: mining systems, mining equipment, excavation, analytical hierarchy process. INTRODUCTION In a micro scale Drmno deposit does not differ from the regional characteristics in the number of The purpose of this paper is to rank mining plies for main coal III Seam. The III Seam and its systems in open pit Drmno as one of the most two plies are present in 60% of drill holes, while in stable mining system for production of lignite the rest of 40% drill holes layering is present with for electricity in power plant in Serbia.