DOCSLIB.ORG

Oxford Philosophy

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Oxford Philosophy OXFORD 2019-20 PHILOSOPHY More pleasant to recollect, at the beginning of the academic 2019-20 Welcome year we welcomed a number of new colleagues as tutorial OXFORD From the Chair of the Faculty Board fellows—Catharine Abell (aesthetics at Queen’s); Alexander Bown and Marion Durand (ancient philosophy at Balliol PHILOSOPHY and Corpus respectively); Will Davies and Matt Parrot (philosophy of mind at St Anne’s and St Hilda’s respectively); and Natalia Waights Hickman (philosophy of action at Worcester). Several of these appointments represented the bringing-back-up-to-number of the fellows in philosophy CONTENTS at the relevant college, following a gap—with St Anne’s and Worcester returning to two fellows after a number of 2 Welcome From the Chair of the Faculty Board: Chris Timpson years, and Balliol (of course, a much-storied college for philosophy) returning to three. 4 News 5 New People Sad news gathered over the winter, however, as we learnt of the deaths of a number of greatly esteemed emeritus 6 Aesthetics in the 21st Century: Catharine Abell, James Grant & Alison Hills colleagues: David Bostock, Myles Burnyeat, Jim Griffin, 10 Philosophy at Oxford 1979-2020: Anita Avramides Rom Harré, John Lucas, and Brian McGuinness. Many of you will have personal memories of these gifted 13 The Story of Academia.edu: Richard Price philosophers and teachers, or will have studied their 16 A Mind Still Valid: Katherine Parkinson works. In my own case, I think particularly of Rom Harré and John Lucas, who were amongst my very first teachers 15 AI Ethics at Oxford: Peter Millican in philosophy of physics (I, conversely, would have been 22 Minds That Speak: Philip Pettit amongst the very last of the students they taught in Oxford). Both played a very significant role in establishing the 25 Recent Books joint schools of Maths and Philosophy and Physics and 26 Obituaries Philosophy in the late 1960s. The very first edition of this magazine, back in 2009, carried a piece about the then-anticipated move of the Faculty to a large, new Humanities building to be built on the Radcliffe Observatory site. This building project ran aground shortly thereafter, in large part a victim to fallout of the 2008 I hope this finds you and yours as well as may be in these financial crisis. A combined Humanities building remained coronavirus-blighted times. Lockdown began a week after an ambition for the Humanities Division, however, and the end of Hilary Full Term. By then the term’s teaching had planning for it was revived over the last couple of years. finished, as had the Hilary Term examinations in philosophy Last June we were delighted to hear of a £150 million (for Psychology, Philosophy, and Linguistics Prelims, and donation from Stephen Schwarzman to fund this new Classics Mods). The great majority of students, following building, which will house seven Humanities Faculties— University and Government guidance, had already gone including Philosophy—and a combined Humanities library. —or were going—out of residence; those unable to do In addition, there will be graduate study spaces, flexible so (including those self-isolating with symptoms) were research space, lecture theatres and performance spaces. looked after in their colleges. Colleagues, both academic The architects (Hopkins) have now been appointed and are and non-academic, worked tremendously hard over the finalising the detailed design, in consultation with Faculties. CONTACT US CREDITS ACKNOWLEDGEMENTS Easter vacation to adjust to home working, and to the needs We still anticipate that the building will open in 2024. As for remote teaching and remote examination in Trinity. well as to us, it will be a home to new activities, some of Oxford Philosophy Editor Paul Lodge The Faculty would like to thank the Library staff in particular pulled off extraordinary feats in which have already begun, including a new initiative in Faculty of Philosophy following people for their kind help making great quantities of study and research material Ethics and AI, which is planned to lead to the foundation Radcliffe Humanities Art Direction Keiko Ikeuchi and assistance: available online, at very short notice. I am very proud of of a new Institute for Ethics in AI within the Faculty. Peter Radcliffe Observatory Quarter & Design www.keiko.camera how everyone has responded. These are testing times, most Millican writes about current Ethics and AI activities at Woodstock Road Jo Kay, Mark Starling, Printed by Oxuniprint especially for our students, who have shown courage and Oxford later in the magazine. Oxford, OX2 6GG UK Bronwyn Travers, Elina Cotterill resilience. As I write, our finalists are embarking on the Chris Timpson first ever online set of exams. Our thoughts are with them, email: [email protected] Professor of the Philosophy of Physics Views expressed in this publication are especially those in the most difficult circumstances, as they Tutorial Fellow in Philosophy, Brasenose College tel: +44 (0)1865 276926 not necessarily those of the Faculty of face up to this unfamiliar challenge. www.philosophy.ox.ac.uk Philosophy or the University of Oxford. 2 | Oxford Philosophy Oxford Philosophy | 3 NEWS NEW PEOPLE Catharine Abell The Queen’s College Catharine joins the Faculty from the University of Manchester, where she was Lecturer, Senior Lecturer and then Reader in Philosophy. From 2006-2010, she was a Macquarie University Research Fellow. She has a PhD from Flinders University and an undergraduate degree from The University of Adelaide. Her research focusses on aesthetics. She has written on the nature and value of art, the expression of emotion, and the nature of genre and its interpretative and evaluative roles. Her research also addresses issues specific to the representational arts, including the nature of depiction, and of cinematic and photographic representation. She has recently completed a book, Fiction, in which she develops an account of fiction as a social practice. Her next research project will address the nature and importance of artistic style. Alexander Bown Balliol College Jake Quilty-Dunn Martin Pickup Amia Srinivasan Rafal Banka Before joining the faculty, Alex had already spent a couple of years at Oxford, as a Career wins the 2020 William wins the Marc Sanders elected as the Chichele joins the Faculty as Development Fellow at The Queen’s College. He was also an undergraduate at Oxford, but James Prize Prize in Metaphysics Professor of Social and recipient of an received his PhD in 2018 from the University of Geneva. He mainly works on issues related to Political Theory ERC Starter Grant logic, epistemology and ontology in ancient philosophy; he is especially interested by the views of at All Souls Hellenistic philosophers and Aristotle on these topics. In recent years, most of his research has focused on the Epicurean school and their attempts to deal with problems such as the status of future contingents, the truth conditions of conditionals, and (something like) the problem of Jake Quilty-Dunn, a Martin Pickup, Turpin Amia Srinivasan, previously The Faculty is delighted induction. postdoctoral research fellow Junior Research Fellow Associate Professor of to begin hosting Rafal on the European Research at Oriel College, has won Philosophy and Tutorial Banka’s three-year research Council-funded project, the Marc Sanders Prize in Fellow at St John’s College, project in comparative Will Davies St Anne’s College Metacognition of Concepts, Metaphysics, a biennial prize was recently elected as the philosophy, which is funded has won the 2020 William awarded by the Marc Sanders Chichele Professor of Social by a prestigious European Will joins the Faculty from the University of Birmingham, where he was Lecturer in Philosophy from James Prize. Foundation to philosophers and Political Theory at All Research Council Starter 2017-19. He studied for the BPhil and DPhil at Balliol College, during which time he was appointed as a Junior Research Fellow at Churchill College, Cambridge. He later held postdoctoral positions who are within 15 years of Souls College. Grant. at the Universities of Antwerp and Oxford. Will’s main research interests are in the philosophy The prize is awarded by the the completion of their PhD. of mind, broadly construed. His main focus is on colour perception; in particular, the nature of Association for the Scientific She is the first woman Rafal, who has expertise colour constancy, and the relationship between colour and form. He is also working on a project Study of Consciousness for Martin was awarded the to hold this prestigious in Chinese philosophy, concerning social explanation in psychiatry. “the most outstanding single prize for his paper ‘The chair, which was previously has joined the Faculty as published contribution to the Situationalist Account of occupied by Isaiah Berlin, a research fellow for the empirical or philosophical Change’. He received a cash Charles Taylor, and Jerry duration of the project from study of consciousness”. prize of $5000 and his paper Cohen. After a BA at Yale, the Jagiellonian University in Marion Durand Corpus Christi College Jake’s winning paper, ‘Is will be published in Oxford Amia completed her BPhil and Cracow. His project aims to Marion joins the faculty from the University of Toronto, where she spent seven years, first as a Iconic Memory Iconic?’, is Studies in Metaphysics. DPhil in Philosophy at Oxford, bring contemporary analytic PhD student and then as a lecturer in the Department of Classics and the Collaborative Program published in Philosophy and More information and a copy initially as a Rhodes Scholar, metaphysics into dialogue in Ancient and Medieval Philosophy. Before that, she had studied Classics as an undergraduate at Phenomenological Research of the paper is available at and then as a Prize Fellow with Chinese philosophy Cambridge. Marion’s primary research is in Stoic philosophy of language with forays into ancient logic and grammar as well as contemporary philosophy of language.
Load more

Recommended publications
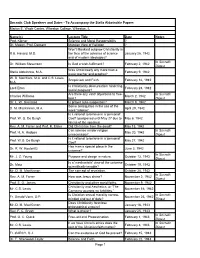
  • Socratic Club Speakers and Dates from the Marion E. Wade Center
    Socratic Club Speakers and Dates - To Accompany the Stella Aldwinckle Papers Marion E. Wade Center, Wheaton College, Wheaton, IL Name(s) Lecture Title Date Notes Prof. Krner Science and Moral Responsibility ? Dr. Mason, Prof. Demant Marxian View of Religion ? Won't Mankind outgrow Christianity in R.E. Havard, M.D. the face of the advance of science January 26, 1942 and of modern ideologies? In Socratic Dr. William Stevenson Is God a wish-fulfilment? February 2, 1942 Digest Was Christ really any more than a Stella Aldwinckle, M.A. February 9, 1942 great teacher and prophet? W. B. Merchant, M.A. and C.S. Lewis, Scepticism and Faith. February 16, 1942 M.A. Is Christianity obscurantism hindering Lord Elton February 23, 1942 social progress? Are there any valid objections to free- In Socratic Charles Williams March 2, 1942 love? Digest Dr. L. W. Grensted Is prayer auto-suggestion? March 9, 1942 Some ambiguities in the use of the D. M. MacKinnon, M.A. April 29, 1942 word 'rational.' Is it rational to believe in a 'personal' Prof. W. G. De Burgh God? (postponed until May 27 due to May 6, 1942 illness of the speaker) Rev. A. M. Farrer and Prof. R. Eisler Did Christ rise from the dead? May 13, 1942 Can science render religion In Socratic Prof. H. A. Hodges May 20, 1942 unnecessary? Digest Is it rational to believe in a 'personal' Prof. W.G. De Burgh May 27, 1942 God? Has man a special place in the Dr. R. W. Kosterlitz June 3, 1942 universe? In Socratic Mr.
    [Show full text]
  • Moral Reason
    Moral Reason OXFORD PHILOSOPHICAL MONOGRAPHS Editorial Committee ANITA AVRAMIDES R. S. CRISP WILLIAM CHILD ANTONY EAGLE STEPHEN MULHALL OTHER TITLES IN THIS SERIES INCLUDE Nietzsche and Metaphysics Peter Poellner Understanding Pictures Dominic Lopes Things That Happen Because They Should: A Teleological Approach to Action Rowland Stout The Ontology of Mind: Events, Processes, and States Helen Steward Wittgenstein, Finitism, and the Foundations of Mathematics Mathieu Marion Semantic Powers: Meaning and the Means of Knowing in Classical Indian Philosophy Jonardon Ganeri Hegel’s Idea of Freedom Alan Patten Metaphor and Moral Experience A. E. Denham Kant’s Empirical Realism Paul Abela Against Equality of Opportunity Matt Cavanagh The Grounds of Ethical Judgement: New Transcendental Arguments in Moral Philosophy Christian Illies Of Liberty and Necessity: The Free Will Debate in Eighteenth-Century British Philosophy James A. Harris Plato and Aristotle in Agreement? Platonists on Aristotle from Antiochus to Porphyry George E. Karamanolis Aquinas on Friendship Daniel Schwartz The Brute Within: Appetitive Desire in Plato and Aristotle Hendrik Lorenz Moral Reason Julia Markovits 1 1 Great Clarendon Street, Oxford, ox2 6dp, United Kingdom Oxford University Press is a department of the University of Oxford. It furthers the University’s objective of excellence in research, scholarship, and education by publishing worldwide. Oxford is a registered trade mark of Oxford University Press in the UK and in certain other countries © Julia Markovits 2014 The moral rights of the author have been asserted First Edition published in 2014 Impression: 1 All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, without the prior permission in writing of Oxford University Press, or as expressly permitted by law, by licence or under terms agreed with the appropriate reprographics rights organization.
    [Show full text]
  • A Simplified Version of Gödel's Theorem Michael Redhead
    A Simplified Version of Gödel’s Theorem Michael Redhead “Isn’t it a bad thing to be deceived about the truth and a good thing to know what the truth is?” Plato Abstract The Lucas - Penrose argument is considered. As a special case we consider sorites arithmetic and explain how the argument actually works. A comparison with Gödel’s own treatment is made. Truth is valuable. But certifiable truth is hard to come by! The Case of Mathematics Does truth equate with proof? No: Gödel showed famously that truth outruns proof, even in the case of the natural numbers 0, 1, 2, 3, … The Lucas-Penrose argument The argument that ascertainable truth outruns proof in mathematics has been used by John Lucas and Roger Penrose to claim that human minds can do things which computers can’t do, and hence that minds can’t be (digital) machines. Quote from Lucas and myself: We are dealing with a different style of reasoning… an informal semantics concerned with truth rather than proof. Sceptics deny that we have such a concept of truth. We cannot prove to them that we have… (but) we have many intimations of truth, not all of which can be articulated as proofs. Sorites arithmetic This is the sort of arithmetic you learnt at school. The basic operation is moving from one number to the next along the number line and repeating the operation a finite number of times. Addition and multiplication are defined recursively in the usual way. So, addition is effectively reduced to adding one and one and one… repeatedly, and multiplication is repeated addition.
    [Show full text]
  • Blackwell Guide to the Philosophy of Religion Blackwell Philosophy Guides Series Editor: Steven M
    The Blackwell Guide to the Philosophy of Religion Blackwell Philosophy Guides Series Editor: Steven M. Cahn, City University of New York Graduate School Written by an international assembly of distinguished philosophers, the Blackwell Philosophy Guides create a groundbreaking student resource – a complete critical survey of the central themes and issues of philosophy today. Focusing and advancing key arguments throughout, each essay incorporates essential background material serving to clarify the history and logic of the relevant topic. Accordingly, these volumes will be a valuable resource for a broad range of students and readers, including professional philosophers. 1 The Blackwell Guide to EPISTEMOLOGY Edited by John Greco and Ernest Sosa 2 The Blackwell Guide to ETHICAL THEORY Edited by Hugh LaFollette 3 The Blackwell Guide to the MODERN PHILOSOPHERS Edited by Steven M. Emmanuel 4 The Blackwell Guide to PHILOSOPHICAL LOGIC Edited by Lou Goble 5 The Blackwell Guide to SOCIAL AND POLITICAL PHILOSOPHY Edited by Robert L. Simon 6 The Blackwell Guide to BUSINESS ETHICS Edited by Norman E. Bowie 7 The Blackwell Guide to the PHILOSOPHY OF SCIENCE Edited by Peter Machamer and Michael Silberstein 8 The Blackwell Guide to METAPHYSICS Edited by Richard M. Gale 9 The Blackwell Guide to the PHILOSOPHY OF EDUCATION Edited by Nigel Blake, Paul Smeyers, Richard Smith, and Paul Standish 10 The Blackwell Guide to PHILOSOPHY OF MIND Edited by Stephen P. Stich and Ted A. Warfield 11 The Blackwell Guide to the PHILOSOPHY OF THE SOCIAL SCIENCES Edited by Stephen P. Turner and Paul A. Roth 12 The Blackwell Guide to CONTINENTAL PHILOSOPHY Edited by Robert C.
    [Show full text]
  • B Academy Review
    The British Academy THE NATIONAL ACADEMY FOR THE HUMANITIES AND SOCIAL SCIENCES REVIEW July – December 2000 The British Academy 10 Carlton House Terrace, London SW1Y 5AH Telephone:020 7969 5200 Fax: 020 7969 5300 Email: [email protected] Web site: www.britac.ac.uk © The British Academy 2001 Some contents of the Review may also be found in electronic form on the Academy’s web site at www.britac.ac.uk Cover illustration: ??????? iii Foreword The British Academy publishes a regular account of its activities by means of its biannual Review. Some readers may be unfamiliar with what the Academy is and what it does.The following pages seek to give a flavour of the variety of Academy activities, which range across a broad spectrum of scholarly endeavour both within the UK and on the international stage. First and foremost, the Academy is a Fellowship of scholars, elected for outstanding academic achievement in one or more of the disciplines of the humanities and social sciences. The active participation of these Fellows enables the Academy to conduct a wide variety of activities to support academic research, to stimulate scholarly debate and to promote the role of the humanities and social sciences to a wider audience. The activities undertaken by the Academy include the organisation of lectures and conferences, the sponsoring of major infrastructural projects that are adopted as Academy Research Projects, running a flourishing publications programme, facilitating international networks, and allocating research awards.This Review contains a section on each of the major areas of the Academy’s work. As well as material customarily to be found in a formal Annual Report, extracts from lectures and publications and specially commissioned articles are included that seek to offer an insight into the variety of academic endeavour promoted by the Academy.
    [Show full text]
  • Gödelian Arguments Against AI
    Gödelian arguments against AI Master’s Thesis ARTIFICIAL INTELLIGENCE Department of Information and Computing Sciences Faculty of Science Utrecht University Author: Jesús Rodríguez Pérez Supervisor: Dr. Gerard Vreeswijk Second reviewer: Prof. Dr. Albert Visser 2015 ii Acknowledgements I would like to thank my supervisor Dr. Gerard Vreeswijk for his guidance and support in this project; for pointing to multiple suggestions and possible improvements regarding not only the content of this thesis, and in particular technical inaccuracies, but most valuably its form and discursive structure. His personal guidance on writing argumentative essays have proved to be a valuable source. I am also indebted to Prof. Dr. Albert Visser for proofreading this text and providing useful feedback in the form of sticky notes. I hope this work reflects the advice that in such respect I received from him. Last, but not least, a word of gratitude goes to my sisters and parents, for the contin- uous loving support they demonstrated me along the way. Without their everyday words of encouragement this thesis would not have come about in its current shape. iii Contents I Predicate logic, axiomatic systems and Gödel’s theorems 4 1 Preliminaries 5 2 The undecidability results 9 2.1 Generalization and acceptance . 10 3 An informal exposition of the proof 15 II The Gödelian arguments and learning systems 21 4 The arguments against Computationalism 22 4.1 Lucas’ argument . 23 4.2 Goedel’s argument . 27 4.3 The counter-argument from the standpoint of mathematical cognition
    [Show full text]
  • BASIL MITCHELL Basil George Mitchell 1917–2011
    BASIL MITCHELL Basil George Mitchell 1917–2011 Career Outline ALTHOUGH BASIL MITCHELL was eventually to make his reputation as a philosopher of religion, his first interests suggested a somewhat different trajectory, perhaps in comparative religion. Born on 9 April 1917 to middle class parents in Bath (his father was a quantity surveyor), it was while living in Southampton that his mother became permanently confined to bed as a result of severe rheumatoid arthritis and remained there for the last twenty years of her life (1928–47). Although Basil was confirmed in the Church of England, his parents’ search for some relief for his mother’s condition led him along with the rest of his family to attend Sufi services of universal worship that included extracts from the sacred texts of all the major religions. Indeed, that search included taking his mother in 1938 to the Paris headquarters of Hazrat Inayat Khan who had brought this par­ ticular version of Sufism from India. Although Basil’s decision to read Greats at The Queen’s College, Oxford was quite conventional, it is signifi­ cant that he confesses to not finding the way philosophy was then taught particularly interesting and that the real satisfaction of his desires came when he was awarded a scholarship to study Indian philosophy under Radhakrishnan, then a professor at Oxford, and began to learn Sanskrit.1 1 Further details are available in Basil’s autobiography, B. G. Mitchell, Looking Back: on Faith, Philosophy and Friends in Oxford (Durham, 2009), and, more briefly, in ‘War and friendship’, in K.
    [Show full text]
  • Oxfordcolleges
    Oxford colleges Oxford University is made up of different colleges. Colleges are academic communities. They are where students usually have their tutorials. Each one has its own dining hall, bar, common room and library, and lots of college groups and societies. If you study here you will be a member of a college, and probably have your tutorials in that college. You will also be a member of the wider University, with access to University and department facilities like laboratories and libraries, as well as hundreds of University groups and societies. You would usually have your lectures and any lab work in your department, with other students from across the University. There is something to be said for an academic atmosphere wherein everyone you meet is both passionate about what they are studying and phenomenally clever to boot. Ziad 144| Does it matter which college I go to? What is a JCR? No. Colleges have a lot more in common than Junior Common Room, or JCR, means two they have differences. Whichever college you go different things. Firstly, it is a room in college: to, you will be studying for the same degree at the a lively, sociable place where you can take time end of your course. out, eat, watch television, play pool or table football, and catch up with friends. The term Can I choose my college? JCR also refers to all the undergraduates in a college. The JCR elects a committee which Yes, you can express a preference. When you organises parties, video evenings and other apply through UCAS (see ‘how to apply’ on p 6) events, and also concerns itself with the serious you can choose a college, or you can make an side of student welfare, including academic ‘open application’.
    [Show full text]
  • Dasgupta UMBC, 1000 Hilltop Circle, Baltimore, Maryland 21250
    A New Approach Refuting Penrose’s Gödelian Argument Arghya Dasgupta UMBC, 1000 Hilltop Circle, Baltimore, Maryland 21250 Abstract Background Related Work Possible Approaches Sir Roger Penrose, though one of the greatest minds in pure In the case of Peano arithmetic or any familiar explicitly Hilary Putnam, G.Boolos and others have already pointed out to know this, we must also prove (or know) that ∀e ∀x(A(e, x) mathematics and physics, is known for his insistence in using axiomatized theory T, it is possible to define the consistency "Con some of Penrose’s technical errors, and he has conceded several ⇒ Φ(e, x)↑ That is, we have to know that A is a sound method Gödel’s incompleteness theorems to support a non-computationist (T)" of T in terms of the non-existence of a number with a certain of the technical points, but there does not seem to be a complete for deciding that our own computations fail to halt: whenever it and even a non-algorithmic view point in studying consciousness. property, as follows: "there does not exist an integer coding a statement of the fundamental problems with this kind of argument. claims that a computation is non-terminating, then in fact that Repeatedly, in books like “The Emperor’s New Mind” (1989), sequence of sentences, such that each sentence is either one of Benacerraf (1967) made two points against the original Lucas computation does not terminate. An alternative resolution of the “Shadows of the Mind” (1994) and “The Large, the Small and the the (canonical) axioms of T, a logical axiom, or an immediate argument, both of which we will develop more precisely here.
    [Show full text]
  • 1 Zuse's Thesis, Gandy's Thesis, and Penrose's Thesis Jack Copeland
    Zuse's Thesis, Gandy's Thesis, and Penrose's Thesis Jack Copeland, Oron Shagrir, Mark Sprevak 1. Introduction Computer pioneer Konrad Zuse (1910-1995) built the world's first working program- controlled general-purpose digital computer in Berlin in 1941. After the Second World War he supplied Europe with cheap relay-based computers, and later transistorized computers. Mathematical logician Robin Gandy (1919-1995) proved a number of major results in recursion theory and set theory. He was Alan Turing's only PhD student. Mathematician Roger Penrose (1931- ) is famous for his work with Stephen Hawking. What we call Zuse's thesis, Gandy's thesis, and Penrose's thesis are three fundamental theses concerning computation and physics. Zuse hypothesized that the physical universe is a computer. Gandy offered a profound analysis supporting the thesis that every discrete deterministic physical assembly is computable (assuming that there is an upper bound on the speed of propagation of effects and signals, and a lower bound on the dimensions of an assembly's components). Penrose argued that the physical universe is in part uncomputable. We explore these three theses. Zuse's thesis we believe to be false: the universe might have consisted of nothing but a giant computer, but in fact does not. Gandy viewed his claim as a relatively apriori one, provable on the basis of a set-theoretic argument that makes only very general physical assumptions about decomposability into parts and the nature of causation. We maintain that Gandy's argument does not work, and that Gandy's thesis is best viewed, like Penrose's, as an open empirical hypothesis.
    [Show full text]
  • 2016 Clifton Henry.Pdf
    The Foundations of Mathematics History, Concepts, and Applications in Higher Level Mathematics by Clifton Henry A CAPSTONE PROJECT submitted in partial fulfillment of the requirements for the acknowledgement Honors Distinction Mathematics School of Engineering, Mathematics, and Science TYLER JUNIOR COLLEGE Tyler, Texas 2016 When people hear the word mathematics, some think numbers and others think solving for x and y. In all truth, the field of mathematics is more than numbers and equations. Mathematics was founded based off the principle of counting in 50,000 B.C.E. Mathematical contributions and ideas increased from the Babylonian Empire in 2000 BC to the 18th century, where mathematicians and philosophers developed ideas in algebra, geometry and calculus. It can be argued that mathematical contributions in the 19th century shaped the field of mathematics and set in place the true foundations of mathematics. In the 19th century, mathematical logic was founded, followed by the development of set theory, and then came the concept of mathematical function. Logic, set theory, and function are some of the foundations of mathematics, and the three revolutionized the field of mathematics as a whole. Mathematical fields, such as topology, abstract algebra, and probability rely heavily on the three foundations. Instead of being seen as numbers and equations, mathematics is the field of logic and proof that is based off the mathematical foundations of logic, set theory, and function. It is important to know how the ideas were developed and put to use in order for mathematics to have its meaning and significance. After understanding how the foundations were developed, it is important to understand how they apply in advanced mathematical fields such as topology, abstract algebra, and probability.
    [Show full text]
  • Logic in Philosophy of Mathematics
    Logic in Philosophy of Mathematics Hannes Leitgeb 1 What is Philosophy of Mathematics? Philosophers have been fascinated by mathematics right from the beginning of philosophy, and it is easy to see why: The subject matter of mathematics| numbers, geometrical figures, calculation procedures, functions, sets, and so on|seems to be abstract, that is, not in space or time and not anything to which we could get access by any causal means. Still mathematicians seem to be able to justify theorems about numbers, geometrical figures, calcula- tion procedures, functions, and sets in the strictest possible sense, by giving mathematical proofs for these theorems. How is this possible? Can we actu- ally justify mathematics in this way? What exactly is a proof? What do we even mean when we say things like `The less-than relation for natural num- bers (non-negative integers) is transitive' or `there exists a function on the real numbers which is continuous but nowhere differentiable'? Under what conditions are such statements true or false? Are all statements that are formulated in some mathematical language true or false, and is every true mathematical statement necessarily true? Are there mathematical truths which mathematicians could not prove even if they had unlimited time and economical resources? What do mathematical entities have in common with everyday objects such as chairs or the moon, and how do they differ from them? Or do they exist at all? Do we need to commit ourselves to the existence of mathematical entities when we do mathematics? Which role does mathematics play in our modern scientific theories, and does the em- pirical support of scientific theories translate into empirical support of the mathematical parts of these theories? Questions like these are among the many fascinating questions that get asked by philosophers of mathematics, and as it turned out, much of the progress on these questions in the last century is due to the development of modern mathematical and philosophical logic.
    [Show full text]