DOCSLIB.ORG

Search and Learning Algorithms for Two-Player Games with Application to the Game of Hex Chao

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Search and Learning Algorithms for Two-Player Games with Application to the Game of Hex Chao Search and Learning Algorithms for Two-Player Games with Application to the Game of Hex by Chao Gao A thesis submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy Department of Computing Science University of Alberta c Chao Gao, 2020 Abstract Two-Player alternate-turn perfect-information zero-sum games have been suggested as a testbed for Artificial Intelligence research since Shannon in 1950s. In this thesis, we summarize and develop algorithms for this line of research. We focus on the game of Hex | a game created by Piet Hein in 1942 and popularized by Jonh Nash in 1949. We continue on previous research, further bringing the strength of machine learning techniques | specifically deep neural networks | to the game of Hex. We develop new methods and apply them to solving and playing Hex. We present state-of-the-art results for Hex and discuss relevant research on other domains. In particular, we develop solving and playing algorithm by combining search and deep learning methods. As a result of our algorithmic innovations, we produce stronger solver and player, winning gold medal at the Computer Olympiad Hex tournaments in 2017 and 2018. ii What I believe is that if it takes 200 years to achieve artificial intelligence, and finally there is a textbook that explains how it is done; the hardest part of that textbook to write will be the part that explains why people didn't think of it 200 years ago, because we are really talking about how to make machines do things that are on the surface of our minds. It is just that our ability to observe our mental processes is not very good and has not been very good. | John McCarthy iii Acknowledgements Many people deserve to be acknowledged for assisting me directly or indirectly in creating this thesis. First of all, I thank my supervisors Ryan Hayward and Martin M¨ullerfor supervising me. My initial interest in games were motivated by my keen interest in playing Chinese chess as a hobby. Even though I roughly know how computers play chess games, I was surprised to learn that super-human strength program does not exist for the game of Hex, especially when considering its simplest rules and straightforward goals. The other aspect of Hex that lures me is its close tie to combinatorics and graphs; these properties have enabled many aspects of Hex be studied in a rigorous mathematical manner rather than mostly empirical as in many other games; I was intrigued to learn more about them, even though I finally did not pursue these directions for my thesis. My study of Hex with deep neural networks was inspired by the consecutive suc- cesses of using deep learning techniques as a general tool for bringing advancement in a number of areas, in particular the early breakthrough in playing the game of Go. By 2016, it becomes clear to me that the next step of research in Hex should be including deep learning to the game. Rather than straightforwardly adapting deep networks into existing Hex algorithms, I tried to understand the essence of each technique thus to invent new paradigms that should be more applicable to Hex and probably other challenging games as well, and this thesis is a reflection of my endeavour towards such an aspiration. In the process, I greatly appreciate the support of Martin M¨uller for his expertise in multiple domains; his critical questions on my work often pushed me to explore important things otherwise I would have neglected. I am greatly grateful to Ryan Hayward for buying two GPU machines to support my research; most experiments in this thesis were carried out on these machines. His attention on writing also influenced me; the little book he gave to me, The Elements of Style, which I originally thought of little use, turned out to be a treasure for providing valuable guidance to me. iv I am also thankful to a number of people who have aided me. Previous re- searchers in Hex including Jakub Pawlewicz, Broderick Arneson, Philip Henderson and Aja Huang have provided me useful comments on codebase benzene. In particu- lar, in 2018 summer, Jakub Pawlewicz helped me greatly for preparing the Computer Hex tournament. Thanks Siqi Yan, Xutong Zhao, Jiahao Li, Paul Banse, Joseph Meleshko, Wai Yi Low and Mengliao Wang for either doing tournament test for me or temporarily contributing their GPU computation for the testing. Nicolas Fabi- ano further discovered more pruning patterns in 2019 summer though these are not discussed in this thesis. Thanks Kenny Young for passing me the working code of MoHex 2.0. I am grateful to Noah Weninger for operating MoHex-CNN in 2017 and helping me produce some training games. Thanks Cybera.ca for providing cloud instances. Thanks Jing Yang for providing his pattern set and useful instructions for 9 9 Hex solution. × I thank the useful discussion on a variety of general topics with Farhad Haqiqat, Chenjun Xiao, Jincheng Mei, Gaojian Fan, Xuebin Qin, Chenyang Huang and Yun- peng Tang; researchers that I known of while I was interning at Borealis AI: Bilal Kartal, Pablo Hernandez Leal, and manager Matt Taylor; my manager at Huawei Edmonton research office Henshuai Yao. Finally, I am deeply grateful to my family for being supportive of my pursuit | I am indebted to my parents, my brother, my sister, and in particular my wife Sitong Li for her great companion, unconditional support and priceless patience. v Contents 1 Introduction 1 1.1 The Game of Hex as a Benchmark for AI . .1 1.2 Searching for Solutions with the Help of Knowledge . .4 1.2.1 Learning Heuristic Knowledge in Games . .6 1.2.2 Principles for Heuristic Search in Games . .9 1.3 Contributions and Organization of This Thesis . .9 2 General and Specific Techniques for Solving and Playing Games 13 2.1 Strategy Representation . 13 2.1.1 Minimax Strategy and Solution Graphs . 13 2.1.2 Strategy Decomposition . 15 2.2 Search and Learning Formulations . 18 2.2.1 State and Problem Space Graphs . 19 2.2.2 Markov Decision Processes and Alternating Markov Games . 21 2.3 Techniques for Strategy Discovery . 23 2.3.1 Informed Best-first Search . 23 2.3.2 Reinforcement Learning . 27 2.3.3 Deep Neural Networks . 30 2.3.4 Combining Learning and Search: Monte Carlo Tree Search . 32 2.4 Hex Specific Research . 33 2.4.1 Complexity of Hex . 33 2.4.2 Graph Properties and Inferior Cell Analysis . 34 2.4.3 Bottom Up Connection Strategy Computation . 37 2.4.4 Iterative Knowledge Computation . 39 2.4.5 Automated Player and Solver . 40 3 Supervised Learning and Policy Gradient Reinforcement Learning in Hex 44 3.1 Supervised Learning with Deep CNNs for Move Prediction . 44 3.1.1 Background . 44 3.1.2 Input Features . 45 3.1.3 Architecture . 45 3.1.4 Data for Learning . 47 3.1.5 Configuration . 48 3.1.6 Results . 48 3.1.7 Discussion . 55 3.2 Policy Gradient Reinforcement Learning . 56 3.2.1 Background . 56 3.2.2 The Policy Gradient in MDPs . 57 3.2.3 An Adversarial Policy Gradient Method for AMGs . 58 3.2.4 Experiment Results in Hex . 61 3.2.5 Setup . 61 3.2.6 Data and Supervised Learning for Initialization . 61 3.2.7 Results of Various Policy Gradient Algorithms . 62 3.2.8 Discussion . 63 vi 4 Three-Head Neural Network Architecture for MCTS and Its Ap- plication to Hex 66 4.1 Background: AlphaGo and Its Successors . 66 4.2 Sample Efficiency of AlphaGo Zero and AlphaZero . 71 4.3 Three-Head Neural Network Architecture for More Efficient MCTS . 73 4.3.1 PV-MCTS with Delayed Node Expansion . 74 4.3.2 Training 3HNN . 76 4.4 Results on 13 13 Hex with a Fixed Dataset . 78 4.4.1 ResNet× for Hex . 78 4.4.2 Setup . 78 4.4.3 Prediction Accuracy of 3HNN . 79 4.4.4 Evaluation in the Integration of PV-MCTS . 81 4.5 Transferring Knowledge Using 3HNN . 83 4.5.1 Setup . 84 4.5.2 Prediction Accuracy In Different Board Sizes . 84 4.5.3 Usefulness When Combined with Search . 85 4.5.4 Effect of Fine-tuning . 87 4.6 Closed Loop Training with 3HNN . 88 4.6.1 Training For 2018 Computer Olympiad . 88 4.6.2 Zero-style Learning . 90 4.7 Discussion . 96 5 Solving Hex with Deep Neural Networks 98 5.1 Focused Proof Number Search for Solving Hex . 98 5.2 Focused Proof Number Search with Deep Neural Networks . 100 5.3 Results on 8 8Hex ........................... 101 5.3.1 Preparation× of Data . 101 5.3.2 Policy and Value Neural Networks . 101 5.3.3 Empirical Comparison of DFPN, FDFPN and FDFPN-CNN 103 5.3.4 Using Three-Head ResNet . 106 5.4 Solving by Strategy Decomposition . 107 6 Conclusions and Future Work 113 References 116 Appendix A Additional Documentation 129 A.1 Neurobenzene . 129 A.2 Visualization for a Human Identified 9 9 Solution . 130 A.3 Published Dataset . .× . 131 A.4 From GBFS to AO* and PNS . 132 A.5 Computing True Proof/Disproof Number is NP-hard . 141 vii List of Tables 2.1 Approximate number of estimated states for N N Hex, N = 9; 10; 11; 13. .......................................× 34 2.2 Evolution of Computer Programs for Playing Hex. 42 3.1 Input features; form bridge are empty cells that playing there forms a bridge pattern. Similarly, an empty cell is save bridge if it can be played as a response to the opponent's move in the bridge carrier.
Load more

Recommended publications
  • Elements of DSAI: Game Tree Search, Learning Architectures
    Introduction Games Game Search Evaluation Fns AlphaGo/Zero Summary Quiz References Elements of DSAI AlphaGo Part 2: Game Tree Search, Learning Architectures Search & Learn: A Recipe for AI Action Decisions J¨orgHoffmann Winter Term 2019/20 Hoffmann Elements of DSAI Game Tree Search, Learning Architectures 1/49 Introduction Games Game Search Evaluation Fns AlphaGo/Zero Summary Quiz References Competitive Agents? Quote AI Introduction: \Single agent vs. multi-agent: One agent or several? Competitive or collaborative?" ! Single agent! Several koalas, several gorillas trying to beat these up. BUT there is only a single acting entity { one player decides which moves to take (who gets into the boat). Hoffmann Elements of DSAI Game Tree Search, Learning Architectures 3/49 Introduction Games Game Search Evaluation Fns AlphaGo/Zero Summary Quiz References Competitive Agents! Quote AI Introduction: \Single agent vs. multi-agent: One agent or several? Competitive or collaborative?" ! Multi-agent competitive! TWO players deciding which moves to take. Conflicting interests. Hoffmann Elements of DSAI Game Tree Search, Learning Architectures 4/49 Introduction Games Game Search Evaluation Fns AlphaGo/Zero Summary Quiz References Agenda: Game Search, AlphaGo Architecture Games: What is that? ! Game categories, game solutions. Game Search: How to solve a game? ! Searching the game tree. Evaluation Functions: How to evaluate a game position? ! Heuristic functions for games. AlphaGo: How does it work? ! Overview of AlphaGo architecture, and changes in Alpha(Go) Zero. Hoffmann Elements of DSAI Game Tree Search, Learning Architectures 5/49 Introduction Games Game Search Evaluation Fns AlphaGo/Zero Summary Quiz References Positioning in the DSAI Phase Model Hoffmann Elements of DSAI Game Tree Search, Learning Architectures 6/49 Introduction Games Game Search Evaluation Fns AlphaGo/Zero Summary Quiz References Which Games? ! No chance element.
    [Show full text]
  • ELF: an Extensive, Lightweight and Flexible Research Platform for Real-Time Strategy Games
    ELF: An Extensive, Lightweight and Flexible Research Platform for Real-time Strategy Games Yuandong Tian1 Qucheng Gong1 Wenling Shang2 Yuxin Wu1 C. Lawrence Zitnick1 1Facebook AI Research 2Oculus 1fyuandong, qucheng, yuxinwu, [email protected] [email protected] Abstract In this paper, we propose ELF, an Extensive, Lightweight and Flexible platform for fundamental reinforcement learning research. Using ELF, we implement a highly customizable real-time strategy (RTS) engine with three game environ- ments (Mini-RTS, Capture the Flag and Tower Defense). Mini-RTS, as a minia- ture version of StarCraft, captures key game dynamics and runs at 40K frame- per-second (FPS) per core on a laptop. When coupled with modern reinforcement learning methods, the system can train a full-game bot against built-in AIs end- to-end in one day with 6 CPUs and 1 GPU. In addition, our platform is flexible in terms of environment-agent communication topologies, choices of RL methods, changes in game parameters, and can host existing C/C++-based game environ- ments like ALE [4]. Using ELF, we thoroughly explore training parameters and show that a network with Leaky ReLU [17] and Batch Normalization [11] cou- pled with long-horizon training and progressive curriculum beats the rule-based built-in AI more than 70% of the time in the full game of Mini-RTS. Strong per- formance is also achieved on the other two games. In game replays, we show our agents learn interesting strategies. ELF, along with its RL platform, is open sourced at https://github.com/facebookresearch/ELF. 1 Introduction Game environments are commonly used for research in Reinforcement Learning (RL), i.e.
    [Show full text]
  • Improved Policy Networks for Computer Go
    Improved Policy Networks for Computer Go Tristan Cazenave Universite´ Paris-Dauphine, PSL Research University, CNRS, LAMSADE, PARIS, FRANCE Abstract. Golois uses residual policy networks to play Go. Two improvements to these residual policy networks are proposed and tested. The first one is to use three output planes. The second one is to add Spatial Batch Normalization. 1 Introduction Deep Learning for the game of Go with convolutional neural networks has been ad- dressed by [2]. It has been further improved using larger networks [7, 10]. AlphaGo [9] combines Monte Carlo Tree Search with a policy and a value network. Residual Networks improve the training of very deep networks [4]. These networks can gain accuracy from considerably increased depth. On the ImageNet dataset a 152 layers networks achieves 3.57% error. It won the 1st place on the ILSVRC 2015 classifi- cation task. The principle of residual nets is to add the input of the layer to the output of each layer. With this simple modification training is faster and enables deeper networks. Residual networks were recently successfully adapted to computer Go [1]. As a follow up to this paper, we propose improvements to residual networks for computer Go. The second section details different proposed improvements to policy networks for computer Go, the third section gives experimental results, and the last section con- cludes. 2 Proposed Improvements We propose two improvements for policy networks. The first improvement is to use multiple output planes as in DarkForest. The second improvement is to use Spatial Batch Normalization. 2.1 Multiple Output Planes In DarkForest [10] training with multiple output planes containing the next three moves to play has been shown to improve the level of play of a usual policy network with 13 layers.
    [Show full text]
  • Unsupervised State Representation Learning in Atari
    Unsupervised State Representation Learning in Atari Ankesh Anand⇤ Evan Racah⇤ Sherjil Ozair⇤ Mila, Université de Montréal Mila, Université de Montréal Mila, Université de Montréal Microsoft Research Yoshua Bengio Marc-Alexandre Côté R Devon Hjelm Mila, Université de Montréal Microsoft Research Microsoft Research Mila, Université de Montréal Abstract State representation learning, or the ability to capture latent generative factors of an environment, is crucial for building intelligent agents that can perform a wide variety of tasks. Learning such representations without supervision from rewards is a challenging open problem. We introduce a method that learns state representations by maximizing mutual information across spatially and tem- porally distinct features of a neural encoder of the observations. We also in- troduce a new benchmark based on Atari 2600 games where we evaluate rep- resentations based on how well they capture the ground truth state variables. We believe this new framework for evaluating representation learning models will be crucial for future representation learning research. Finally, we com- pare our technique with other state-of-the-art generative and contrastive repre- sentation learning methods. The code associated with this work is available at https://github.com/mila-iqia/atari-representation-learning 1 Introduction The ability to perceive and represent visual sensory data into useful and concise descriptions is con- sidered a fundamental cognitive capability in humans [1, 2], and thus crucial for building intelligent agents [3]. Representations that concisely capture the true state of the environment should empower agents to effectively transfer knowledge across different tasks in the environment, and enable learning with fewer interactions [4].
    [Show full text]
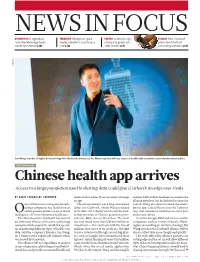
  • Chinese Health App Arrives Access to a Large Population Used to Sharing Data Could Give Icarbonx an Edge Over Rivals
    NEWS IN FOCUS ASTROPHYSICS Legendary CHEMISTRY Deceptive spice POLITICS Scientists spy ECOLOGY New Zealand Arecibo telescope faces molecule offers cautionary chance to green UK plans to kill off all uncertain future p.143 tale p.144 after Brexit p.145 invasive predators p.148 ICARBONX Jun Wang, founder of digital biotechnology firm iCarbonX, showcases the Meum app that will use reams of health data to provide customized medical advice. BIOTECHNOLOGY Chinese health app arrives Access to a large population used to sharing data could give iCarbonX an edge over rivals. BY DAVID CYRANOSKI, SHENZHEN medical advice directly to consumers through another $400 million had been invested in the an app. alliance members, but he declined to name the ne of China’s most intriguing biotech- The announcement was a long-anticipated source. Wang also demonstrated the smart- nology companies has fleshed out an debut for iCarbonX, which Wang founded phone app, called Meum after the Latin for earlier quixotic promise to use artificial in October 2015 shortly after he left his lead- ‘my’, that customers would use to enter data Ointelligence (AI) to revolutionize health care. ership position at China’s genomics pow- and receive advice. The Shenzhen firm iCarbonX has formed erhouse, BGI, also in Shenzhen. The firm As well as Google, IBM and various smaller an ambitious alliance with seven technology has now raised more than US$600 million in companies, such as Arivale of Seattle, Wash- companies from around the world that special- investment — this contrasts with the tens of ington, are working on similar technology. But ize in gathering different types of health-care millions that most of its rivals are thought Wang says that the iCarbonX alliance will be data, said the company’s founder, Jun Wang, to have invested (although several big play- able to collect data more cheaply and quickly.
    [Show full text]
  • Fml-Based Dynamic Assessment Agent for Human-Machine Cooperative System on Game of Go
    Accepted for publication in International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems in July, 2017 FML-BASED DYNAMIC ASSESSMENT AGENT FOR HUMAN-MACHINE COOPERATIVE SYSTEM ON GAME OF GO CHANG-SHING LEE* MEI-HUI WANG, SHENG-CHI YANG Department of Computer Science and Information Engineering, National University of Tainan, Tainan, Taiwan *[email protected], [email protected], [email protected] PI-HSIA HUNG, SU-WEI LIN Department of Education, National University of Tainan, Tainan, Taiwan [email protected], [email protected] NAN SHUO, NAOYUKI KUBOTA Dept. of System Design, Tokyo Metropolitan University, Japan [email protected], [email protected] CHUN-HSUN CHOU, PING-CHIANG CHOU Haifong Weiqi Academy, Taiwan [email protected], [email protected] CHIA-HSIU KAO Department of Computer Science and Information Engineering, National University of Tainan, Tainan, Taiwan [email protected] Received (received date) Revised (revised date) Accepted (accepted date) In this paper, we demonstrate the application of Fuzzy Markup Language (FML) to construct an FML- based Dynamic Assessment Agent (FDAA), and we present an FML-based Human–Machine Cooperative System (FHMCS) for the game of Go. The proposed FDAA comprises an intelligent decision-making and learning mechanism, an intelligent game bot, a proximal development agent, and an intelligent agent. The intelligent game bot is based on the open-source code of Facebook’s Darkforest, and it features a representational state transfer application programming interface mechanism. The proximal development agent contains a dynamic assessment mechanism, a GoSocket mechanism, and an FML engine with a fuzzy knowledge base and rule base.
    [Show full text]
  • Spy on Me #2 – Artistic Manoevres for the Digital Present
    Spy on Me Artistic Manoeuvres for the Digital Present #2 19. –29.3.2020 Spy on Me #2 – Artistic Manoeuvres for the Digital Present 19.–29.3.2020 / HAU1, HAU2, HAU3 We have arrived in the reality of digital transformation. Life with screens, apps and algorithms influences our behaviour, our atten - tion and desires. Meanwhile the idea of the public space and of democracy is being reorganized by digital means. The festival “Spy on Me” goes into its second round after 2018, searching for manoeuvres for the digital present together with Berlin-based and international artists. Performances, interactive spatial installati - ons and discursive events examine the complex effects of the digi - tal transformation of society. In theatre, where live encounters are the focus, we come close to the intermediate spaces of digital life, searching for ways out of feeling powerless and overwhelmed, as currently experienced by many users of internet-based technolo - gies. For it is not just in some future digital utopia, but here, in the midst of this present, that we have to deal with the basic conditi - ons of living together as a society and of planetary survival. Are we at the edge of a great digital darkness or at the decisive tur - ning point of perspective? A Festival by HAU Hebbel am Ufer. Funded by: Hauptstadtkulturfonds. What is our rela - tionship with alien conscious - nesses? As we build rivals to human intelligence, James Bridle looks at our relationship with the planet’s other alien consciousnesses. 5 On 27 June 1835, two masters of the ancient DeepBlue defeated Garry Kasparov at chess, prise, strangeness and even horror that Chinese game of Go faced off in a match up to that point a game with Go-like status as AlphaGo evokes will become a feature of more which was the culmination of a years-long a bastion of human imagination and mental and more areas of our lives.
    [Show full text]
  • Understanding & Generalizing Alphago Zero
    Under review as a conference paper at ICLR 2019 UNDERSTANDING &GENERALIZING ALPHAGO ZERO Anonymous authors Paper under double-blind review ABSTRACT AlphaGo Zero (AGZ) (Silver et al., 2017b) introduced a new tabula rasa rein- forcement learning algorithm that has achieved superhuman performance in the games of Go, Chess, and Shogi with no prior knowledge other than the rules of the game. This success naturally begs the question whether it is possible to develop similar high-performance reinforcement learning algorithms for generic sequential decision-making problems (beyond two-player games), using only the constraints of the environment as the “rules.” To address this challenge, we start by taking steps towards developing a formal understanding of AGZ. AGZ includes two key innovations: (1) it learns a policy (represented as a neural network) using super- vised learning with cross-entropy loss from samples generated via Monte-Carlo Tree Search (MCTS); (2) it uses self-play to learn without training data. We argue that the self-play in AGZ corresponds to learning a Nash equilibrium for the two-player game; and the supervised learning with MCTS is attempting to learn the policy corresponding to the Nash equilibrium, by establishing a novel bound on the difference between the expected return achieved by two policies in terms of the expected KL divergence (cross-entropy) of their induced distributions. To extend AGZ to generic sequential decision-making problems, we introduce a robust MDP framework, in which the agent and nature effectively play a zero-sum game: the agent aims to take actions to maximize reward while nature seeks state transitions, subject to the constraints of that environment, that minimize the agent’s reward.
    [Show full text]
  • Computer Go: from the Beginnings to Alphago Martin Müller, University of Alberta
    Computer Go: from the Beginnings to AlphaGo Martin Müller, University of Alberta 2017 Outline of the Talk ✤ Game of Go ✤ Short history - Computer Go from the beginnings to AlphaGo ✤ The science behind AlphaGo ✤ The legacy of AlphaGo The Game of Go Go ✤ Classic two-player board game ✤ Invented in China thousands of years ago ✤ Simple rules, complex strategy ✤ Played by millions ✤ Hundreds of top experts - professional players ✤ Until 2016, computers weaker than humans Go Rules ✤ Start with empty board ✤ Place stone of your own color ✤ Goal: surround empty points or opponent - capture ✤ Win: control more than half the board Final score, 9x9 board ✤ Komi: first player advantage Measuring Go Strength ✤ People in Europe and America use the traditional Japanese ranking system ✤ Kyu (student) and Dan (master) levels ✤ Separate Dan ranks for professional players ✤ Kyu grades go down from 30 (absolute beginner) to 1 (best) ✤ Dan grades go up from 1 (weakest) to about 6 ✤ There is also a numerical (Elo) system, e.g. 2500 = 5 Dan Short History of Computer Go Computer Go History - Beginnings ✤ 1960’s: initial ideas, designs on paper ✤ 1970’s: first serious program - Reitman & Wilcox ✤ Interviews with strong human players ✤ Try to build a model of human decision-making ✤ Level: “advanced beginner”, 15-20 kyu ✤ One game costs thousands of dollars in computer time 1980-89 The Arrival of PC ✤ From 1980: PC (personal computers) arrive ✤ Many people get cheap access to computers ✤ Many start writing Go programs ✤ First competitions, Computer Olympiad, Ing Cup ✤ Level 10-15 kyu 1990-2005: Slow Progress ✤ Slow progress, commercial successes ✤ 1990 Ing Cup in Beijing ✤ 1993 Ing Cup in Chengdu ✤ Top programs Handtalk (Prof.
    [Show full text]
  • 6 Adversarial Search
    6 ADVERSARIAL SEARCH In which we examine the problems that arise when we try to plan ahead in a world where other agents are planning against us. 6.1 GAMES Chapter 2 introduced multiagent environments, in which any given agent will need to con- sider the actions of other agents and how they affect its own welfare. The unpredictability of these other agents can introduce many possible contingencies into the agent’s problem- solving process, as discussed in Chapter 3. The distinction between cooperative and compet- itive multiagent environments was also introduced in Chapter 2. Competitive environments, in which the agents’ goals are in conflict, give rise to adversarial search problems—often GAMES known as games. Mathematical game theory, a branch of economics, views any multiagent environment as a game provided that the impact of each agent on the others is “significant,” regardless of whether the agents are cooperative or competitive.1 In AI, “games” are usually of a rather specialized kind—what game theorists call deterministic, turn-taking, two-player, zero-sum ZERO­SUM GAMES games of perfect information. In our terminology, this means deterministic, fully observable PERFECT INFORMATION environments in which there are two agents whose actions must alternate and in which the utility values at the end of the game are always equal and opposite. For example, if one player wins a game of chess (+1), the other player necessarily loses (–1). It is this opposition between the agents’ utility functions that makes the situation adversarial. We will consider multiplayer games, non-zero-sum games, and stochastic games briefly in this chapter, but will delay discussion of game theory proper until Chapter 17.
    [Show full text]
  • "Large Scale Monte Carlo Tree Search on GPU"
    Large Scale Monte Carlo Tree Search on GPU GPU+HK大ávモンテカルロ木探索 Doctoral Dissertation ¿7論£ Kamil Marek Rocki ロツキ カミル >L#ク Submitted to Department of Computer Science, Graduate School of Information Science and Technology, The University of Tokyo in partial fulfillment of the requirements for the degree of Doctor of Information Science and Technology Thesis Supervisor: Reiji Suda (½田L¯) Professor of Computer Science August, 2011 Abstract: Monte Carlo Tree Search (MCTS) is a method for making optimal decisions in artificial intelligence (AI) problems, typically for move planning in combinatorial games. It combines the generality of random simulation with the precision of tree search. Research interest in MCTS has risen sharply due to its spectacular success with computer Go and its potential application to a number of other difficult problems. Its application extends beyond games, and MCTS can theoretically be applied to any domain that can be described in terms of (state, action) pairs, as well as it can be used to simulate forecast outcomes such as decision support, control, delayed reward problems or complex optimization. The main advantages of the MCTS algorithm consist in the fact that, on one hand, it does not require any strategic or tactical knowledge about the given domain to make reasonable decisions, on the other hand algorithm can be halted at any time to return the current best estimate. So far, current research has shown that the algorithm can be parallelized on multiple CPUs. The motivation behind this work was caused by the emerging GPU- based systems and their high computational potential combined with the relatively low power usage compared to CPUs.
    [Show full text]
  • Combining Tactical Search and Deep Learning in the Game of Go
    Combining tactical search and deep learning in the game of Go Tristan Cazenave PSL-Universite´ Paris-Dauphine, LAMSADE CNRS UMR 7243, Paris, France [email protected] Abstract Elaborated search algorithms have been developed to solve tactical problems in the game of Go such as capture problems In this paper we experiment with a Deep Convo- [Cazenave, 2003] or life and death problems [Kishimoto and lutional Neural Network for the game of Go. We Muller,¨ 2005]. In this paper we propose to combine tactical show that even if it leads to strong play, it has search algorithms with deep learning. weaknesses at tactical search. We propose to com- Other recent works combine symbolic and deep learn- bine tactical search with Deep Learning to improve ing approaches. For example in image surveillance systems Golois, the resulting Go program. A related work [Maynord et al., 2016] or in systems that combine reasoning is AlphaGo, it combines tactical search with Deep with visual processing [Aditya et al., 2015]. Learning giving as input to the network the results The next section presents our deep learning architecture. of ladders. We propose to extend this further to The third section presents tactical search in the game of Go. other kind of tactical search such as life and death The fourth section details experimental results. search. 2 Deep Learning 1 Introduction In the design of our network we follow previous work [Mad- Deep Learning has been recently used with a lot of success dison et al., 2014; Tian and Zhu, 2015]. Our network is fully in multiple different artificial intelligence tasks.
    [Show full text]