Functional Quantization Vinith Misra
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Food for Feeling Great Part 1
SPRING 2011 True $5.00 Natural Health The Magazine of the Natural Health Society of Australia Food for feeling great Part 1 - fresh fruits Safe breast screening Teen anger - why? Our amazing feet Bowen Therapy Veggie garden, Part 2 – spring planting Recipes - from Laos An unusual new study Editorial Imagine my surprise when a young naturo- product promoted in this magazine is first This issue initiates a series path phoned and said she is looking for vetted by us. Quite often, there is a fasci- of articles on the different “unvaccinated adults” to participate in a nating and passionate story behind how food categories, Part 1 covering study to investigate the health of people the proprietor became interested in the fresh fruits. We also continue the series who have never been vaccinated. What product in the first place. In this issue, we on veggie gardening with Part 2. a great idea! Come to think of it, this is present two such stories. Vegetarian restaurants are not only found something that the medical authorities Joe Ciancio markets an air purifier-ioniser in Sydney! We branch out to Adelaide in should have done long. (which keeps the pollutants within itself), this issue, and will present restaurants in Because vaccination has become a because he had discovered – almost to other states in future issues. In fact, our sacred cow in Australia, it is very difficult his peril – the dangers of polluted air and readers may be able to make some rec- to obtain objective information about water. His eye-opening story is on page 14. -

Adult-Catalogue-Jul-Dec-2020 Web.Pdf
Spine: 7.3mm July – December 2020 4 Original Fiction 14 Raven Books – Crime, Thriller & Mystery 20 Original Non-Fiction 46 Cookery 54 Paperback Fiction 60 Paperback Non-Fiction 74 Bloomsbury Business 78 Sigma – Popular Science 82 Green Tree – Wellbeing 86 Bloomsbury Sport & Wisden 94 Yearbooks 98 Bloomsbury Contact List & International Sales 101 Social Media Contacts 102 Index export information TPB Trade Paperback PAPERBACK B format paperback (dimensions 198 mm x 129 mm) ORIGINAL FICTION 4 ORIGINAL FICTION Why Visit America Matthew Baker A twisted, exhilarating and darkly strange vision of our time, explored in thirteen interconnected episodes young man breaks the news to his family that he is going to A transition from an analogue body to a digital existence. A man returns home after committing a great crime, his sentence being that his memory, and thereby his entire life, is wiped clean. The citizens of Plainfield, Texas, have had it with the United States. So they decide to secede, rename themselves America in memory of their former country, and set themselves up to receive tourists from their closest neighbour: America. The stories in Matthew Baker’s collection portray a world within touching distance of our own. This is an America riven by dilemmas confronting so many of us – from old age to consumerism, drugs to internet culture – turned on its head by one of the most darkly innovative and defiantly strange voices of the moment. 04 AUGUST 2020 IMPRINT: BLOOMSBURY PUBLISHING Matthew Baker is the author of the story collection Hybrid EXPORT TPB / 9781526618399 / £13.99 Creatures. His stories have appeared in the Paris Review, American HARDBACK / 9781526618382 / £14.99 EBOOK / 9781526618405 / £12.58 Short Fiction, New England Review, One Story, Electric Literature TERRITORY: COMMONWEALTH (EXCLUDING CANADA)/ and Conjunctions, and in anthologies including Best of the Net UK/OPEN MARKET and Best Small Fictions. -

Corus Entertainment New and Returning Specialty Series 2020-2021
CORUS ENTERTAINMENT NEW AND RETURNING SPECIALTY SERIES 2020-2021 LIFESTYLE Food Network Canada Bakeaway Camp with Martha Stewart (4x60) – NEW SERIES – (Fall 2020) Six talented home baker campers brave the outdoor elements for a once-in-a-lifetime opportunity to perfect their skills under the watchful eye of host Jesse Palmer, baking mentor Martha Stewart and her camp counselors, baking experts Carla Hall and Dan Langan. Equal parts baking boot camp and camp- inspired games and challenges, the bakers compete in two rounds, with the most-impressive baker of the first heat getting a one-on-one mentoring session with Martha in her home kitchen. The baker that displays the least amount of progress will pack their bags and head home, and the last camper standing wins a bake-tacular kitchen filled with appliances worth $25,000! Beat Bobby Flay (27x30) – NEW EPISODES – (Fall 2020) On Beat Bobby Flay skilled chefs compete for the opportunity to cook against culinary master Bobby. The action starts with two talented cooks going head to head in a culinary battle, and the winner proceeds to round two for the ultimate food face off against the famed chef. Big Food Bucket List, Season 2 (26x30) – NEW SEASON – (Corus Studios/Lone Eagle Entertainment) (Fall 2020, Winter 2021) In season 2 of Big Food Bucket List, Host John Catucci (You Gotta Eat Here!) is back to take viewers on a brand-new food adventure across North America as he checks buzz-worthy, crazy, delicious food off his bucket list. In each episode, John visits the restaurants behind these must-eat meals and hits the kitchen to learn how the chefs make their mind-blowing creations. -

Develo Tries to Brin Reta Bac to Broad
ROETareRA. = Scho Memoria Danc The School Noteboo Honor Joh Pitrellj Pag 12 By Jim McCrann Hig School Writer “One da we tried to cut out from school. We were half down way to Calda Pizza wh en about 20 kids came Tunning out shoutin “Pitrelli’s in there! Run!” I was wearing Hicksville my jacket and Mr. Pitrellj ‘yelled ‘Yo! Hicksville! Tarn Incorporatin The Hicksville around! Get back to school Edition of the now! I want Mid-Island Herald you in my office—now!’ Mr. Pitrelli ILLUSTRATED got into his car and he was smokin NEWS his pipeandhe pulled rh overnext tous and said, Vol. ‘Get back to clas 3 No. 36 Hicksville, N.Y. and and we& © forge about Thursday, February 16 1989 1989 Anton the 35¢ per copy Communit Newspapers of Lon island whol thing’ It was the All Rights Reserved. funniest thing.” Central Office Phone: 747-8282 This Hicks High School student and many others hav stories to tell abou the late Jo Pitrelli,an Tries to administrative assistant who Develo Brin Reta Bac to Passed away last August. Although a Broad disciplinaria Mr. Pitrelli was respected Rita his by By Langdon students. If a request b a real estate Hicksville students held develop is a danc in his approved by the town board, memory residents may last Thursda It was an event to soon be able to sho on as “honor aman Broadwa the who somehow touched all once did of before the state widened the road us,” accordi to student bod almost president, 1 years ago. -

British TV Streaming Guide
NETFLIX Website: http://netflix.com Description: One of the biggest and oldest streaming services, Netflix offers a wide variety of content from all over the world - along with quite a bit of their own original content. Available On: Roku, Fire TV, Apple TV, Apple iPhone & iPad, Chromecast, Fire tablets, select Smart TVs, Android phones and tablets, and computer (via web browser). Cost: $8.99/month (1 screen), $12.99 HD (2 screens same time), $15.99 UHD (4 screens same time) Now Streaming Mysteries & Crime Dramas The A List - 2018 - This series blends The Five – 2016 - Years after a young boy romance, drama, suspense, and mystery disappears, his DNA turns up at a crime when a group of young women go to a scene. Based on the novel by Harlen remote camp with a supernatural Coben. presence. The Frankenstein Chronicles – 2015 to Broadchurch – 2013 to 2017 - When an 11- 2017 - In 1827 London, a detective hunts a year-old boy is murdered in a quiet coastal killer with an appetite for dismemberment. community, town secrets are exposed. Giri/Haji - 2019 - Japanese detective Kenzo David Tennant (Deadwater Fell) and Olivia Mori travels to London to figure out Colman (Rev) star. whether his brother Yuto, presumed dead, Collateral – 2018 - When a pizza delivery is actually dead. Yuto is believed to have man is gunned down in London, DI Kip killed the nephew of a Yakuza member, Glaspie refuses to accept that it's just a and the search draws Kenzo into the dark random act of violence. Her investigation and dangerous criminal underworld of drags her into a dark underworld she never London. -

PWCF News the Newsletter of Prader-Willi California Foundation an Affiliate Of
PWCF News The Newsletter of Prader-Willi California Foundation An Affiliate of April-June, 2010 ~ Volume 20, Number 2 Prader-Willi Syndrome Benefit Concert Craneway Pavilion—Billy Hustace Photography Get your groove on while you raise awareness of Prader-Willi syndrome and funds for PWCF. Make it a Date Night! Come out to the extraordinary Craneway Pavilion, enjoy a delicious dinner at the Boilerhouse Restaurant and a fantastically fun evening of rock ‘n roll! Tell your neighbors, invite your friends! Ticket sales benefit Prader-Willi California Foundation. For more information contact PWCF 310-372-5053 or 800-400-9994 within California. Sandi & The RockerFellers Friday, July 16, 2010 at 8:00 p.m. Sandi Snyder - Lead Vocals Craneway Pavilion Skip Snyder - Lead Guitar & Vocals 1414 Harbour Way S Ken Fisher - Bass Guitar Richmond, CA 94804 Art Beringer - Drums Tickets are $5 at the door Enjoy rock, blues and jazz influences from '70s Ten minutes from Berkeley through today including songs played by bands such as The Pretenders, Sheryl Crow, Bonnie Raitt, Five minutes from Richmond/San Rafael Bridge Lynyrd Skynyrd, Train, No Doubt, Huey Lewis and Fifteen minutes from San Francisco Bay Bridge Craneway.com // CranewayBlog.com many others. Boilerhouse Restaurant 510.215.6000 In This Issue: Parent to Parent on Sex Education 3 Call for Board Candidates 11 Growth Hormone: Long Term Safety 6 Experience with Depo-Provera 13 In The Trenches Part I 7 Marriage & Family Part II 15 Walking for PWS Events 8 Ride The Wave 18 PRADER-WILLI PWS Support Contacts -

Taapsee Pannu
FOR THE MAN IN FULL | www.mansworldindia.com MAY 2020 | K 150 TA APSEE PANNU WRITING HER OWN SCRIPT Executive Editor’s Note MAY 2020 Publisher & Editor N RADHAKRISHNAN THE ART OF ENJOYING ONE’S Executive Publisher MINAL SURVE Executive Editor ARNESH GHOSE COMPANY, MERGE DRAGONS, Associate Editor RAJU BIST AND MY RELATIONSHIP Assistant Editor SAMREEN TUNGEKAR WITH SUGAR Fashion Editor NEELANGANA VASUDEVA Art Director TANVI SHAH Associate Art Director HEMALI LIMBACHIYA can be used, but multiple book plots were graphed. I had to work out — Graphic Designers GAUTAMI DAVE, SANJANA SUVARNA the sweaty kind — at least four times a week. I played a lot of chess and Scrabble with my partner. I got better at chess. I, funnily, sucked ass at JAYESH V. SALVI Senior Digital Manager Scrabble. I have no idea why and I am deeply ashamed. But those games Production Manager MANGESH SALVI kept me alert. And I took to Merge Dragons like an addict. mansworldindia.com Okay, hear me out. Merge Dragons is an elaborate online game — the ads kept popping up during scrabble — which involves various Web Editor ARNESH GHOSE challenges that help you build your own dragon farm and base camp and Staff WritersMAYUKH MAJUMDAR, SANIKA ACHREKAR, RAJEEV MATHEW fill it up with gold and construction and orchards and magic mushrooms, and look at me, sounding like an absolute idiot. Merge Dragons seems Consulting Editor PABLO CHATERJI like a cross between Farmville and Candy Crush (I’ve played neither; I’m have never been someone who cannot be by himself. It’s weird, just aware of the concepts) and funnily it gave me a sense of purpose MAITHILI RAO, SOLEIL NATHWANI, Contributing Editors I know. -

March 2013.Indd
IL POSTINO VOL. 14 NO. 7 MARCH 2013 :: MARZO 2013 $2.00 Il Postino Goes to South Florida! Palm Beach 2013 IL POSTINO • OTTAWA, ONTARIO, CANADA www.ilpostinocanada.com Page 2 IL POSTINO MARCH 2013 IL POSTINO Letters to the Editor 865 Gladstone Avenue, Suite 101 • Ottawa, Ontario K1R 7T4 Letters to the Editor (613) 567-4532 • [email protected] www.ilpostinocanada.com Cari Editori, Publisher Preston Street Community Foundation desidero farvi conoscere, con preghiera di informare la nostra comunità, che oggi è arrivato in sede l’Ambasciatore Gian Lorenzo Cornado accompagnato dalla Italian Canadian Community Centre moglie Martine. L’Ambasciatore Cornado assume la direzione dell’Ambasciata dopo of the National Capital Region Inc. aver gia’ prestato servizio in Canada quale Primo Segretario ad Ottawa (1987-1992) e quale Console Generale a Montreal e Rappresentante Permanente presso l’ICAO Executive Editor (2000-2004). Angelo Filoso Per vostra utilità, vi allegao ancge una sua fotografia. Managing Editor Marcus Filoso Per ogni altra informzione relativa al suo curricul vitae, potete visitare il sito dell’Ambasciata www.ambottawa.esteri.it. Layout & Design Ringraziandovi per la collaborazione, vi invito cordiali saluti. Marcus Filoso Alessandro Giuliani Web Site Design & Hosting Assistente Amministrativo Thenewbeat.ca Ambasciata d’Italia, Ottawa Printing Winchester Print & Stationary Dear Postino Canada, Special thanks to these contributors for this issue I really like your website! I work at a TV production company and have a great short video that we hope you can Gino Bucchino, Dosi Contreneo, Laura D’Amelio, Lina feature on your site – you can embed it from Youtube if you wish. -

Dairy Digest 2014 Index of Advertisers
SDSU Dairy Digest2014 Out with the old. In with the BLUE.A Publication of the South Dakota State University Dairy Club PROUD TO BE FAMILY OWNED AND AMERICAN MADE TABLE OF CONTENTS Digest Staff……………………………………......…4 Index of Advertisers……………………...........….5 Dedication……………………………………......….6 Department Highlights…………………............…..7 Dean’s Comments…………………………........….8 Advisor’s Comments……………………….........…9 South Dakota Dairy Princess Highlights…….......10 17 Minnesota Dairy Princess Highlights……….......11 2013 President’s Comments……………............12 2014 President’s Comments……………............13 Class Pictures………………………………….......15 Dairy Products Judging……………………..........17 North American Dairy Challenge……….............18 Dairy Challenge Academy…………………..........19 Senior Spotlights……………………………….......20 Holiday Cheese Box Fundraiser…………..........26 Internship Spotlights…………………………........28 Jackrabbit Dairy Drive………………………….....40 Dairy Club Christmas Tree…………………….....41 Campus-wide Ag Day…………………………......42 18 Adopt-A-Highway……………………………….....43 Little International…………………………….........44 Special Olympics…………………………….........46 Ag-Bio Ice Cream Social…………………….........47 Dairy Cattle Judging in Texas…………….............48 Jackrabbit Dairy Camp……………………...........50 Dairy Cattle Judging at World Dairy Expo…….....51 South Dakota State Fair……………………...........52 Midwest Regional Dairy Challenge……..............54 Faculty Spotlights…………………………….........56 Graduate Student Spotlights……………..........…70 ADSA-SAD………………………………………80 Candids......................................................83 -
Shondaland's Netflix Debut
December 2020 -January 2021 Shondaland’s Netflix debut Television www.rts.org.uk September 2013 1 DRAMA Heartfelt confessions and last-minute reprieves. Big reveals and characters in crisis. Discover a world of drama through music and bring your story to life. SEND US YOUR BRIEF DISCOVER MORE [email protected] audionetwork.com/discover Journal of The Royal Television Society December 2020/January 2021 l Volume 58/1 From the CEO Farewell, then, to 2020, and a more recent remote encounter Do read our report of the recent a year that we will all with a mystery entrepreneur’s butler. “Can TV save the planet?” event and find hard to forget. I was delighted by the inspirational this issue’s Our Friend column, writ- What better guide to and heartfelt message from the RTS’s ten by the new RTS Midlands Chair, the past 12 months royal patron, HRH The Prince of Wales, Kuljinder Khaila. Both have important than the always bril- to the TV sector’s production workers, messages for our challenging times. liant Sir Peter Bazal- delivered at last month’s RTS Craft & Finally, a happy new year to you gette. His review of 2020 might make Design Awards. all. I hope you get some proper down- you laugh and cry, as he eloquently HRH’s belief that the TV workforce time after a difficult year. Take care of sums up the year of Covid-19 and will rebound stronger than ever from yourselves and your families. Black Lives Matter. these challenging times is one we Baz also recalls a tense moment on should all take to heart. -
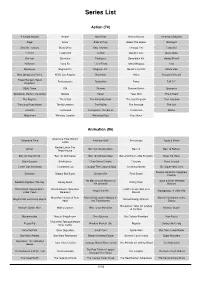
Series List 2021-05-15
Series List Action (74) A Simple Murder Airwolf Alex Rider Almost Human American Odyssey Angel Arrow Birds of Prey Blade: The Series Blindspot Blood & Treasure Blood Drive Blue Thunder Chicago Fire Cobra Kai Condor Crackdown Curfew Deadly Class Deep State Die Hart Dominion Flashpoint Generation Kill Hawaii Five-0 Helstrom Kung Fu L.A.'s Finest Lethal Weapon Lost MacGyver Magnum P.I. Magnum, P.I. Marvel's Iron Fist Miami Vice Most Dangerous Game NCIS: Los Angeles Naxalbari Nikita Person of Interest Power Rangers Beast Professionals Revolution Rome S.W.A.T. Morphers SEAL Team SIX Shooter Shrikant Bashir Spartacus Spartacus: Gods of the Arena Spooks Taken Teen Wolf The A-Team The Fugitive The Gifted The Incredible Hulk The Last Kingdom The Librarians The Long Road Home The Musketeers The Pacific The Passage The Unit Timeless Torchwood Transporter: The Series Treadstone Walker Watchmen Whiskey Cavalier Wynonna Earp Your Honor Animation (96) Adventure Time: Distant Adventure Time American Dad! Animaniacs Apple & Onion Lands Barbie: Life In The Archer Be Cool, Scooby-Doo! Ben 10 Ben 10 Reboot Dreamhouse Ben 10: Alien Force Ben 10: Omniverse Ben 10: Ultimate Alien Ben and Holly's Little Kingdom Bless the Harts Bob's Burgers Brickleberry Chop Socky Chooks Clarence Close Enough Corner Gas Animated Counterfeit Cat Courage The Cowardly Dog Crossing Swords DC Super Hero Girls Foster's Home For Imaginary Dicktown Dragon Ball Super Duncanville Final Space Friends He-Man and the Masters of Jayce and the Wheeled Freedom Fighters: The Ray Harley Quinn -

RTS Announces Winners for the RTS Craft
PRESS RELEASE ROYAL TELEVISION SOCIETY ANNOUNCES WINNERS FOR THE CRAFT & DESIGN AWARDS 2020 • Michaela Coel receives RTS Special Award for I May Destroy You • Outstanding Achievement Award presented to renowned casting director Nina Gold • Special message to the industry from HRH The Prince of Wales London, 23 November 2020 – The Royal Television Society (RTS), Britain’s leading forum for television and related media, has announced the winners of the prestigious RTS Craft & Design Awards 2020, supported by Netflix, via an online celebration this evening. Hosted by radio broadcaster, actor and spoken word artist Mim Shaikh, the virtual event also included a special message from RTS Patron, HRH The Prince of Wales, in which he highlighted the challenges and praised the ingenuity and resourcefulness seen across the television industry over the past year, and celebrated the international recognition of the quality of content produced in the UK. The RTS Craft & Design Awards celebrate excellence in broadcast television and aim to recognise the huge variety of skills and processes involved in programme production. Across the 31 competitive categories, the BBC led the way with 19 wins, three of which were for the BBC One & HBO series His Dark Materials for the Design – Titles, Effects, and Production Design – Drama categories. ITV and Channel 4 each took home four awards with ITV’s The Masked Singer garnering the Costume Design - Entertainment & Non Drama, and documentary For Sama winning two awards for Channel 4 for Director – Documentary/Factual & Non Drama and Music – Original Score. The RTS Special Award was presented to Michaela Coel for her BBC One and HBO hit series I May Destroy You.