DOCSLIB.ORG

Improving a Virtual Race Car Performance Using MSC.ADAMS/Car-Motorsports and Modefrontier

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Improving a Virtual Race Car Performance Using MSC.ADAMS/Car-Motorsports and Modefrontier Improving a virtual race car performance using MSC.ADAMS/Car-MotorSports and modeFrontier modeFrontier User’s Meeting Trieste, Italy Sep 2004 Diego Minen Eddi Valvason Special Project Development Group MSCSoftware Courtesy of AUDI Sport Courtesy of SAUBER F1 Courtesy of Williams F1 Agenda Basic elements for Race Car Simulation System Level Approach for Race Simulation Multibody vehicle model Chassis Engine, GearBox, Differential, Driveline Tires Aerodynamics Track profile Driver Model Simulation Types Exploration of the limits=> Process Integration Functional Virtual Race Vehicle Track Data 3D CAD Test Data Flexibility Aerodynamics Controls/Hydraulics Success – at Audi Sport Business: Automotive Race Manufacturer Challenge: Re-enter Sport Racing at Le Mans Solution: Virtual race car + track; rapid design iteration Value: 1999 : 3rd 2000 : 1st, 2nd, & 3rd 2001 : 1st & 2nd 2002 : 1st, 2nd, & 3rd 2003 : 1st, 2nd (Bentley) 2004 : private team victory “…procedures to optimize vertical dynamics, aerodynamic, mechanical setup and differential setup at the same time simulating a high dynamic kerb crossing have been investigated… simulation helps to understand how to improve performance of a complex race vehicle...“ --Dr. Martin Mühlmeier Vehicle Dynamics AUDI Sport AG Ingolstadt Success – at N.Technology Business: Motorsport competitions (ETCC, Rally) Challenge: To shorten development cycle while improving the over all performance Solution: Use ADAMS/Motorsport (Analyses: Suspension, 4post testrig, ADAMS/Insight, AeroLap, Close Loop Track Simulations) Value: Won TCC Championship in 2001, 2002 and 2003. “Using ADAMS/Motorsport allows us to build and tune suspension subsystems in a more productive way before going on the test track. Running sensitivity studies with hundreds of different configurations is now a matter of minutes. ADAMS/Motorsport gives us also the possibility to have all important parameters under control.” -- Guido Pasquino Head of Calculation Dept. ADAMS/MotorSports Outline Aston Martin NewmanHaas CART Audi Sport AG NTech BAR F1 Panther Racing Dallara Automobili Patrick Racing Dunlop MotorSports UK Penske (IRL & NASCAR) DODGE Motorsports Porsche Ferrari F1 PPI Motorsports Ford MotorSports Prodrive Gforce SAUBER F1 Goodyear Tire Co. Solution F. GM MotorSports Team Rosberg F3 HWA-AMG Racing Toyota F1 Jaguar F1 Team Menard IRL Jasper Motorsports Team Mo Nonn IRL Lotus Engineering Williams F1 MultiMatic CAR/MS CAR PRE/MS CAR&PRE The Vehicle Model Assembly Template Component Data Files Files (Teim Orbit) E ADAMS L Suspensions Dampers C Engine Map I Chassis Bushings Vehicle H E Steering Bumpstops Model V Brakes Tires ... ... Vehicle+Road+Driver System Toe Course Data File N O Camber I A (Teim Orbit) System & Analysis T Caster T Configuration A A P Ride height R D U 2D or 3D - Springs Static Sim U T profile D Steering Pad Fuel G Driver E I A Step Steer F S Driver Mass Open Loop O Racing Line Double Lane Driver path N Machine Ballast R Data Driven ... Max Xls O Human ... C The Simulation Requirements Basic elements for Race Car Simulation Simulation Types Quasi-Static Testrigs Suspension 2D or 3D Tracks Open or Closed Even road profile Dynamic Testrigs Tires MultiPostRigs 2D or 3D Tracks Open Loop Closed Loop (limit performance Driver Model) Even or uneven road profile Real Time SmartDriver Architecture SmartDriver is a feedback controller: it receives as inputs the sensor measurements and provides the vehicle controls: steering, throttle, User Inputs: Task Planner -driving style brake, clutch and gear commands -driving task on line learning -… The control actions depend only on past and Trajectory Planner present measurements r e Motion Controller v i s l e It mimics human driving on one hand and drive r n n D a h t c r the vehicle to its dynamic limits of performance on n Perception channels o a i t a u t m c the other A S The two different control tasks are taken into ACAR Model Tire Model Road Builder account and can be both fullfilled thanks a 2D Aero Model 3D Model Based Predictive Controller technique Robustness and, consequently, limited need of Road Model tuning is the crucial requirement SmartDriver Machine Controller desired velocity desired yaw rate on connecting contour actual yaw rate Yaw rate control path geometry Control of Lateral Dynamics ADAMS Vehicle Model Road Model Throttle velocity r e Clutch Acceleration l l Brake gear o r t Gear RPM n o C Control of Long Dynamics n o i t o Trajectory Planner M The program drives the vehicle along a desired path, given as a curve in 3D at velocity v(s) SmartDriver provides default inputs to the vehicle at a frequency of 100Hz: MACHINE driving The outer control loop uses a one track nonholonomic vehicle model and computes an optimal feasible vehicle trajectory up to the time horizon, or “preview time”, Tp From the current position to Tp, SD controls the vehicle yaw rate The inner control loop acts on steering, throttle and brake to best track the yaw rate profile determined above SmartDriver at Max Speed - MSC.Track Requirements for Improvements Identify component data from experimental analysis Tires Exploration of the limits with the full car model MultiObjective Optimization Handling Tire Magic Formula Identification EExxaammpplele: :P Paacceejijkikaa 9 944 [L[LAATTEERRAALL__CCOOEEFFFFICICIEIENNTTSS] ] aa00 = = n nuummbbeerr aa11 = = nnuummbbeerr Identification Process aa22 = = n nuummbbeerr aa33 = = n nuummbbeerr aa44 = = n nuummbbeerr Experimental Data have been considered as data to identify aa55 = = n nuummbbeerr aa66 = = n nuummbbeerr aa77 = = n nuummbbeerr Virtual Tyre Model the Magic Formula is commonly used to calculate the aa88 = = n nuummbbeerr aa99 = = n nuummbbeerr aa1100 = = n nuummbbeerr steady-state and transient behavior of handling tire. It’s a set of aa111111 = = n nuummbbeerr aa111122 = = n nuummbbeerr aa1122 = = n nuummbbeerr mathematical formulas based on the physical behavior of the tire, road, aa1133 = = n nuummbbeerr aamm00 = = n nuummbbeerr and the tire-to-road contact; it calculates the forces (Fx, Fy) and moments aamm11 = = n nuummbbeerr aamm22 = = n nuummbbeerr aamm33 = = n nuummbbeerr (Mx, My, Mz) acting on the tyre under pure and combined slip conditions, aamm44 = = n nuummbbeerr aamm55 = = n nuummbbeerr aamm66 = = n nuummbbeerr using longitudinal and lateral slip( , ), wheel camber ( ) and the vertical aamm77 = = n nuummbbeerr aamm88 = = n nuummbbeerr force (Fz) as inputs aamm99 = = n nuummbbeerr EExxaammpplele: :P Paacceejkjkaa9944 - -LLaateteraral lFFoorcrceeEEqquuaatitoionnss Softwares Used: CC==aa00 DD==(a(a11**FFZZ++aa22)*)*FFZZ**RROOAADDMMUU TireBuilder Æ generation of the lateral force BBCCDD==aa33**SSININ(A(ATTAANN(F(FZZ/a/a44)*)*22.D.D00)*)*(1(1.0.0-a-a55**AABBSS(G(GAAMMMMAA))) BB==BBCCDD/(/C(C**DD)) curves SShh==aa88**GGAAMMMMAA++aa99**FFZZ++aa1100 SSvv==(a(a111122**FFZZ++aa111111)*)*FFZZ**GGAAMMMMAA++aa1122**FFZZ++aa1133 PHI=(1-E)*(DELTA+Sh)+E/B*ATAN(B*(DELTA+Sh)) Excel Æ formulating of relaxation length eqs PHI=(1-E)*(DELTA+Sh)+E/B*ATAN(B*(DELTA+Sh)) EE==(a(a66**FFZZ++aa77) ) CCGG==aamm00 Æ modeFRONTIER used as identifiction tool AAGG==aamm11 BBGG==aamm22**CCOOSS(A(ATTAANN(a(amm33**(D(DEELLTTAA-a-amm44)))) TARGET: Create automatically a TIR file to reproduce GGaa00==aamm66**FFZZ++aamm77 FFyy00==DD**SSININ(C(C**AATTAANN(B(B**PPHHI)I)+)+SSvv the experimental tire curves FFyyxxgglil=i=SSININ(1(1.9.9**AATTAANN(a(amm88**KKAAPPPPAA))) FFyyxxddeel=l=CCOOSS(A(ATTAANN(a(amm99**DDEELLTTAA))) FFyyxx==aamm55**FFZZ**(G(GAAMMMMAA-G-Gaa00)*)*FFyygglil*i*FFyyddeel l FFyy==FFyy00**CCOOSS(C(CGG**AATTAANN(B(BGG**(K(KAAPPPPAA-A-AGG)))/)C/COOSS(C(CGG**AATTAANN(-(B-BGG**AAGG))+)+FFyyxx Handling Tire Magic Formula Identification Identification Targets Tire Lateral Response [ Fy = Fy(D,Fz) ] V Relaxation Length [ D] ­ ª º½ ­ª CP § 180 ·º FL ½ ° Fz ° ¡ V V o ® ¨ ¸ ¾ o Pty1 SIN ®Pty2 ATAN « »¾ R0 « S » LS 2 ° « Fz0 Pty3 »° ¯¬ © ¹¼ ¿ ¯ ¬ ¼¿ Tire Lateral Response Identification Process The methodology has been structured in the following way: Experimental Data: 8 lateral force curves: 4 Fz values 2 camber values 128 check points (16 for each experimental curve) Æ the objective is made by the sum of the difference between the target point and the point evaluated from Tire_Builder: OBJ ¦ >ABS Pti Pi @ i where “i” Æ [1,...,112] All the Pacejka Pure-Lateral Coefficients (18 coeff) have been considered as input variable for the IP The TIR file considered is based on the MF Tyre model. All Pacejka Pure-Lateral Coefficients have been considered, and during the IP each coeff has been changed of ± 50% with respect its original value. From the optimization point of view the problems is equivalent to find the minimum of an objective function which is mathematically defined as: n m f : where: n: it represents the number of the input variables Æ 18 m: it represents the number of the objective Æ 1 Tire Lateral Response Identification Process Structure 1. The experimental tire curves are considered as the target for the IP (i.e. Curves representing Æ Lateral Forces, Aligning Moments Æ as function of different Normal Forces, Camber and Lateral Slip Angles,...) 2. For each curve a certain number of check points has been chosen, in order to compare them with those calculated with Tire_Builder during the IP Æ or during the variation of the Pacejka coefficients in the TIR file • 16 check points for each curve • 4 Fz values • 2 camber values For a total of: • 8
Load more

Recommended publications
  • Triple Champion René Rast: “The DTM Has Always Been My Home”
    Audi MediaInfo Triple champion René Rast: “The DTM has always been my home” • The big champion’s interview with the Audi factory driver • From the Audi RS 5 DTM to the Audi e-tron FE07 • Double program possible in Formula E and DTM Neuburg a. d. Donau, November 18, 2020 – The future is electric, also for René Rast. The most successful Audi DTM driver of all time will take part in the FIA Formula E World Championship for Audi in 2021, but the 34-year-old father of a family has also already set his next goal in the DTM. With his third title triumph in just four years, René Rast wrote DTM history at the beginning of November. The Minden-born driver, who lives in Bregenz (Austria), won 24 races in record time with the Audi RS 5 DTM, took 20 pole positions, set the fastest lap 14 times and collected 1,113 points. With 77 starts, this corresponds to an average of more than 14 points per race. In the DTM’s eternal list of best drivers, René Rast is now tied with racing legend Klaus Ludwig in second place for championship titles. In this interview, the German explains how he spent the days after winning his third title, which goals he has for Formula E, why he remains loyal to Audi and which DTM record he still wants to break. How does this sound: three-time DTM champion and on a par with a legend like Klaus Ludwig? Of course, it is a very special feeling to be among the three best DTM drivers in history.
    [Show full text]
  • Customer Teams Field Five Audi R8 LMS Cars at the DTM Season Opener at Monza
    Audi MediaInfo Customer teams field five Audi R8 LMS cars at the DTM season opener at Monza • Customer teams ABT Sportsline and Rosberg field five GT3 sports cars • Sophia Flörsch contests first DTM race Neuburg a. d. Donau, June 16, 2021 – The DTM starts its 36th season under new auspices in which Audi is strongly represented on two grids. While the DTM is relying on GT3 sportscars like the Audi R8 LMS for the first time after two decades of Class 1 touring cars, the DTM Trophy is tackling its second season with production-based models like the Audi R8 LMS GT4. “Audi knows the DTM very well and, with twelve title successes in the drivers classification alone, is one of the two most successful brands in history. A new era begins for the DTM in 2021. Gerhard Berger has succeeded in transforming the Class 1 era into a highly attractive platform based on GT motorsport. The 2021 season promises pure excitement thanks to a high level of brand diversity and an internationally top-class driver line-up,” says Julius Seebach, Managing Director Audi Sport GmbH and responsible for motorsport at Audi. “For our Audi Sport customer racing customers, the new DTM platform offers the opportunity to fight for the coveted DTM title. With the R8 LMS, we offer the product that is capable of winning and are pleased that the teams have chosen Audi.” As usual, two races are scheduled for each of the eight events. They usually last 55 minutes plus one lap and include one mandatory pit stop each.
    [Show full text]
  • MOTORSPORTS a North Carolina Growth Industry Under Threat
    MOTORSPORTS A North Carolina Growth Industry Under Threat A REPORT PREPARED FOR NORTH CAROLINA MOTORSPORTS ASSOCIATION BY IN COOPERATION WITH FUNDED BY: RURAL ECONOMIC DEVELOPMENT CENTER, THE GOLDEN LEAF FOUNDATION AND NORTH CAROLINA MOTORSPORTS FOUNDATION October 2004 Motorsports – A North Carolina Growth Industry Under Threat TABLE OF CONTENTS Preliminary Remarks 6 Introduction 7 Methodology 8 Impact of Industry 9 History of Motorsports in North Carolina 10 Best Practices / Competitive Threats 14 Overview of Best Practices 15 Virginia Motorsports Initiative 16 South Carolina Initiative 18 Findings 20 Overview of Findings 21 Motorsports Cluster 23 NASCAR Realignment and Its Consequences 25 Events 25 Teams 27 Drivers 31 NASCAR Venues 31 NASCAR All-Star Race 32 Suppliers 32 Technology and Educational Institutions 35 A Strong Foothold in Motorsports Technology 35 Needed Enhancements in Technology Resources 37 North Carolina Motorsports Testing and Research Complex 38 The Sanford Holshouser Business Development Group and UNC Charlotte Urban Institute 2 Motorsports – A North Carolina Growth Industry Under Threat Next Steps on Motorsports Task Force 40 Venues 41 Sanctioning Bodies/Events 43 Drag Racing 44 Museums 46 Television, Film and Radio Production 49 Marketing and Public Relations Firms 51 Philanthropic Activities 53 Local Travel and Tourism Professionals 55 Local Business Recruitment Professionals 57 Input From State Economic Development Officials 61 Recommendations - State Policies and Programs 63 Governor/Commerce Secretary 65 North
    [Show full text]
  • 2009 Deutsche Tourenwagen Masters
    2009 Deutsche Tourenwagen Masters The 2009 Deutsche Tourenwagen Masters was the twenty-third season of premier German 2009 Deutsche Tourenwagen touring car championship and also tenth season under the moniker of Deutsche Tourenwagen Masters Masters since the series' resumption in 2000. The series began on 17 May at Hockenheim and Previous: 2008 Next: 2010 finished on 25 October at the same venue. Support series: Formula 3 Euro Series Timo Scheider successfully defended his championship title, taking his Audi A4 to a five-point Timo Scheider defend his second Deutsche Tourenwagen Masters Drivers' Championship while Gary Paffett (right) finished second in the championship. series win over Mercedes-Benz driver Gary Paffett. Contents Teams and drivers Driver changes Technical changes Race calendar and results Season results Championship standings Teams' championship References External links Teams and drivers Of the nineteen drivers that competed in the 2008 season, only Bernd Schneider and Christijan Albers did not return. Rookies in 2009 are the Kolles Futurecom trio of Christian Bakkerud, Johannes Seidlitz and Tomáš Kostka. The following manufacturers, teams and drivers competed in the 2009 Deutsche Tourenwagen Masters. All teams competed with tyres supplied by Dunlop. Make Car Team No. Drivers Rounds 1 Timo Scheider[1] All 2 Tom Kristensen[1] All Audi A4 DTM 2009 Abt Sportsline 5 Mattias Ekström[1] All 6 Martin Tomczyk[1] All 21 Katherine Legge[1] All 11 Mike Rockenfeller[1] All Audi Team Rosberg Audi A4 DTM 2008 12 Markus Winkelhock[1]
    [Show full text]
  • STARTERLISTE 2005 FORMULA 3 EURO SERIES Nr
    STARTERLISTE 2005 FORMULA 3 EURO SERIES Nr. Nation Fahrer Bewerber Fahrzeug Team Motor 1 GBR Lewis Hamilton ASM F3 Dallara F305/021 ASM F3 Mercedes 2 GER Adrian Sutil ASM F3 Dallara F305/059 ASM F3 Mercedes 2 GER Maximilian Götz ASM F3 Dallara F305/059 ASM F3 Mercedes 3 FRA Loïc Duval Signature-Plus Dallara F305/036 Signature Opel 4 GBR James Rossiter Signature-Plus Dallara F305/029 Signature Opel 5 JPN Kohei Hirate Team Rosberg Dallara F305/003 Team Rosberg Opel 6 NED Giedo van der Garde Team Rosberg Dallara F305/039 Team Rosberg Opel 7 BRA Lucas di Grassi Manor Motorsport Dallara F305/025 Manor Motorsport Mercedes 7 BRA Lucas di Grassi Manor Motorsport Dallara F305/062 Manor Motorsport Mercedes 8 GBR Paul di Resta Manor Motorsport Dallara F305/020 Manor Motorsport Mercedes 9 GER Sebastian Vettel ASL Mücke Motorsport Dallara F305/011 Mücke Motorsport Mercedes 10 BRA Átila Abreu ASL Mücke Motorsport Dallara F305/028 Mücke Motorsport Mercedes 11 BEL Greg Franchi Prema Powerteam Dallara F305/004 Prema Powerteam Opel 12 ITA Marco Bonanomi Prema Powerteam Dallara F305/026 Prema Powerteam Opel 14 BRA Fábio Carbone Signature SLC R1/001 Signature Opel 15 FRA Guillaume Moreau Signature Dallara F305/035 Signature Opel 16 ESP Alejandro Núñez HBR Motorsport Dallara F305/027 HBR Motorsport Opel 17 GER Maximilian Götz HBR Motorsport Dallara F305/040 HBR Motorsport Opel 17 GBR Danny Watts HBR Motorsport Dallara F305/040 HBR Motorsport Opel 18 ARG Esteban Guerrieri Team Midland Euroseries Dallara F305/034 Team Midland Euroseries Toyota 19 USA Richard
    [Show full text]
  • DTM Hockenheimring Hockenheimring BW, Length 4574 M 06
    DTM Hockenheimring Hockenheimring BW, length 4574 m 06. - 08.11.2020 DTM Result race 1, 07.11.2020 A M E N D E D -Reg.No.: R-12025-A/20 Rk No DRIVER/ENTRANT CAR LAPS TIME GAP INT km/h BEST IN 1 51 Nico Müller (CHE) Audi Sport Team Abt SportslineCastrol EDGE Audi RS 5 DTM 36 1:01:11.045 161.477 1:31.039 19 2 33 René Rast (DEU) 0.622 Audi Sport Team RosbergAudi Sport RS 5 DTM 36 1:01:11.667 0.622 161.450 1:30.487 22 3 53 Jamie Green (GBR) 0.411 Audi Sport Team RosbergAkrapovic Audi RS 5 DTM 36 1:01:12.078 1.033 161.432 1:31.472 21 4 28 Loic Duval (FRA) 3.927 Audi Sport Team PhoenixBMC Air Filter Audi RS 5 DTM 36 1:01:16.005 4.960 161.259 1:31.231 22 5 27 Jonathan Aberdein (RSA) 1.620 BMW Team RMRCATL BMW M4 DTM 36 1:01:17.625 6.580 161.188 1:31.861 20 6 99 Mike Rockenfeller (DEU) 0.031 Audi Sport Team PhoenixTwin Busch Audi RS5 DTM 36 1:01:17.656 6.611 161.187 1:31.428 12 7 4 Robin Frijns (NLD) 0.116 Audi Sport Team Abt SportslineAral Ultimate Audi RS 5 DTM 36 1:01:17.772 6.727 161.182 1:30.907 11 8 8 Robert Kubica (POL) 1.941 ORLEN Team ART (ART Grand Prix) BMW M4 CLASS1 36 1:01:19.713 8.668 161.097 1:32.030 22 9 25 Philipp Eng (AUT) 0.357 BMW Team RBMZF BMW M4 DTM 36 1:01:20.070 9.025 161.081 1:32.212 21 10 31 Sheldon Van der Linde (RSA) 2.031 BMW Team RBMShell BMW M4 DTM 36 1:01:22.101 11.056 160.992 1:31.480 18 11 62 Ferdinand Habsburg (AUT) 1.590 WRT Team Audi SportWRT Audi RS 5 DTM 36 1:01:23.691 12.646 160.923 1:31.653 23 12 22 Lucas Auer (AUT) 2.598 BMW Team RMRBMW Bank M4 DTM 36 1:01:26.289 15.244 160.810 1:32.934 20 13 13 Fabio
    [Show full text]
  • Investment for Growth Machining Centres & Probing
    CNC Machining Spring00 4/24/00 11:07 AM Page 1 volume 4 number 13 spring 2000 TheThe NewNew NationwideNationwide HFOHFO NetworkNetwork HMCsHMCs CrankCrank UpUp ProductionProduction MixingMixing MethodsMethods andand MachinesMachines forfor FlexibilityFlexibility TrainingTraining forfor thethe FutureFuture InvestmentInvestment forfor GrowthGrowth JobJob ShopShop TakesTakes OffOff CuttingCutting TitaniumTitanium CNC Machining Spring00 4/24/00 11:07 AM Page 2 photo by Mike Reyno © Skytech Images > volume 4 > number 13 > spring 2000 > CONTENTS FEATURES hat goes around, comes around. No, wait, that’s not it. What Kellogg Cranks Up Production 6 comes around, goes around? Nope, that’s not it either. How about: What goes around and around? Yeah, that’s it. Horizontals in the Mix at Hobart 10 W Now that you’re totally confused, I’ll explain. The above is just a Titanium Hog Breeds Success 14 roundabout way to convey that this issue of CNC Machining is filled with DeLong and Short of a Family Business 26 things that go around. From helicopters, to crankshafts, to mixers, the stories revolve around things that rotate. Haas & Renishaw Fuel Growth 32 Our cover story this time around features MB Manufacturing and Tooling Corporation, a relatively young job shop that cut its teeth hogging out titanium INDUSTRYNEWS blocks for helicopter rotor components. After reaching a turning point in his life, owner Mike Bramlage decided to quit the rat race and set off on his own. With little Editorial: The Changing Face of Distribution 2 more than two years under its belt, his shop has turned the corner and become a very Haas Factory Outlets Dominate Market 3 profitable venture.
    [Show full text]
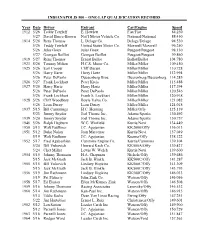
  • One Lap Record
    INDIANAPOLIS 500 – ONE-LAP QUALIFICATION RECORDS Year Date Driver Entrant Car/Engine Speed 1912 5/26 Teddy Tetzlaff E. Hewlett Fiat/Fiat 84.250 5/27 David Bruce-Brown Nat’l Motor Vehicle Co. National/National 88.450 1914 5/26 Rene Thomas L. Delage Co. Delage/Delage 94.530 5/26 Teddy Tetzlaff United States Motor Co. Maxwell/Maxwell 96.250 5/26 Jules Goux Jules Goux Peugeot/Peugeot 98.130 5/27 Georges Boillot Georges Boillot Peugeot/Peugeot 99.860 1919 5/27 Rene Thomas Ernest Ballot Ballot/Ballot 104.780 1923 5/26 Tommy Milton H.C.S. Motor Co. Miller/Miller 109.450 1925 5/26 Earl Cooper Cliff Durant Miller/Miller 110.728 5/26 Harry Hartz Harry Hartz Miller/Miller 112.994 5/26 Peter DePaolo Duesenberg Bros. Duesenberg/Duesenberg 114.285 1926 5/27 Frank Lockhart Peter Kreis Miller/Miller 115.488 1927 5/26 Harry Hartz Harry Hartz Miller/Miller 117.294 5/26 Peter DePaolo Peter DePaolo Miller/Miller 120.546 5/26 Frank Lockhart Frank S. Lockhart Miller/Miller 120.918 1928 5/26 Cliff Woodbury Boyle Valve Co. Miller/Miller 121.082 5/26 Leon Duray Leon Duray Miller/Miller 124.018 1937 5/15 Bill Cummings H.C. Henning Miller/Offy 125.139 5/23 Jimmy Snyder Joel Thorne Inc. Adams/Sparks 130.492 1939 5/20 Jimmy Snyder Joel Thorne Inc. Adams/Sparks 130.757 1946 5/26 Ralph Hepburn W.C. Winfield Kurtis/Novi 134.449 1950 5/13 Walt Faulkner J.C. Agajanian KK2000/Offy 136.013 1951 5/12 Duke Nalon Jean Marcenac Kurtis/Novi 137.049 5/19 Walt Faulkner J.C.
    [Show full text]
  • Fernandez Media Guide 06
    Team Information At-A-Glance MEDIA CONTACT: DREW BROWN Team Lowe’s Racing 1435 W. Morehead St, Ste 190 Charlotte, NC 28208 Tel: 704.714.4305 Cell: 704.650.0428 Email: [email protected] TAMY VALKOSKY Fernández Racing 17 El Prisma Rancho Santa Margarita, CA 92688 Tel: 949.459.9172 Cell: 949.842.3946 Email: [email protected] MEDIA RESOURCES: Additional information on Lowe’s Fernández Racing and the Rolex Series can be found at: media.lowesracing.com www.fernandezracing.net www.grandamerican.com GRAND AMERICAN ROAD RACING ASSOCIATION Adam Saal, Director of Communications Tel: 386.947.6681 Email: [email protected] MEDIA REFERENCE: OFFICIAL TEAM NAME: Lowe’s Fernández Racing FOUNDED: December 2005 OWNERS: Fernández Racing (Adrián Fernández, Tom Anderson) HEADQUARTERS: 6835 Guion Road Indianapolis IN 46268 317.299.5100 317.280.3051 Fax DRIVERS: Adrián Fernández and Mario Haberfeld ENTRY: No. 12 Lowe’s Fernández Racing Pontiac Riley KEY PERSONNEL: Tom Anderson, Managing Director Steve Miller, Team Manager Mike Sales, Chief Mechanic John Ward, Race Engineer Lowe’s Fernández Racing to Compete for 2006 Rolex Series Championship LOWE’S AND FERNÁNDEZ RACING ANNOUNCED the creation of of Key Biscayne, Fla., is a former British Formula 3 champion, who made Lowe’s Fernández Racing on January 4 of this year. The team will field the his US racing debut in the Champ Car World Series contesting the 2003 No. 12 Lowe’s Fernandez Racing Pontiac Riley Daytona Prototype for and 2004 seasons. drivers Adrián Fernández and Mario Haberfeld in the 14-race Grand “This is an honor for me to join Adrián Fernández, who I have admired American Rolex Sports Car Series.
    [Show full text]
  • DIA Group Faces Audit
    PULLOUT SECTION INSIDE: TV LISTINGS FOR THE WEEK JUNE 29-JULY 5, 1997 THE DETROITEtW VOL. 2 NO. 33 75 CENTS S unday To u r n a l CONTINUING THE STRUGGLE FOR JUSTICE AND CONTRACTS ©TDSJ SPECIAL SECTION INSIDE DIA group A c t io n! M o to w n M e m o r ie s faces audit City official questions Founders So By Paige St. John But in the 1970s, when a Journal Staff Writer financial crisis nearly crippled Detroit’s chief financial watch­ the DIA, the society began tak­ dog has ordered a special audit ing a more aggressive role in its of the nonprofit group that is try­operations. Currently it raises ing to gain control of the Detroitthe lion’s share of the DIA’s Institute of Arts. annual $34-million budget, is The audit comes in the midst responsible for all fund-raising, of a controversial push by Mayoroversees millions of dollars in Dennis Archer to remove the cityendowments and runs such aux­ from daily operation of the pub­iliary departments as its gift lic museum. shop and its photography Auditor general Joseph Harris department. said last week he is struck by the The city, meanwhile, has final absence of independent informa­say over the budget and policy tion on the Founders Society’sdecisions. About half of the claim that the DIA cannot sur­museum’s employees, including vive unless the Society is given thea director, curators, guards 20-year contract to run theand janitors, work for the city. museum as it sees fit.
    [Show full text]
  • TRACKSIDE 2016 Welcome to the Firestone 600, the Ninth Round of the 2016 Verizon Indycar Series Season
    VERIZON INDYCAR SERIES TRACKSIDE 2016 Welcome to the Firestone 600, the ninth round of the 2016 Verizon IndyCar Series season. The INDYCAR and Texas Motor Speedway communications staffs are here to assist. Direct questions and requests to a member of either staff in the media center. INDYCAR Communications Contacts Mike Kitchel, Director, Communications P: (317) 492-6453 C: (317) 716-5256 [email protected] Pat Caporali, Senior Manager, Media Relations P: (317) 492-4547 C: (317) 447-5789 [email protected] • Kate Guerra, Senior Manager, Advance Communications P: (317) 492-8577 C: (317) 800-8438 [email protected] Mark Robinson, Senior Manager, Editorial P: (317) 492-8538 C: (317) 308-1464 [email protected] Cathy Kightlinger, Manager, Lifestyle Communications P: (317) 492-8534 C: (317) 797-3490 [email protected] Arni Sribhen, Coordinator, Media Relations P: (317) 492-8531 C: (317) 506-4816 [email protected] Texas Motor Speedway Media Relations Contacts: Mike Zizzo, Vice President, Media Relations P: (817) 215-8520 C: (817) 528-4676 [email protected] Gregg Elkin, Manager, Media Relations P: (817) 215-8523; C: 817 937-9206, [email protected] Louis Mora, Manager, Media Relations P: (817) 215-8521; C: (817) 528-3769, [email protected] INDYCAR Media Website – media.indycar.com A media-only section of INDYCAR’s website is available at media.indycar.com. The site contains content about the Verizon IndyCar Series, including: INDYCAR, Verizon IndyCar Series and Mazda Road to Indy logos
    [Show full text]
  • Mercado De 800 Millones De Consumidores En El Asesinato Del Ex Canciller Letelier È Economía /Finanzas È Internacional
    México Firmó TLC con la Unión Europea; Revelan Documento que Implica a Pinochet Mercado de 800 Millones de Consumidores en el Asesinato del ex Canciller Letelier è Economía /Finanzas è Internacional Año 48, Número 15,333 Colima, Col., Viernes 24 de Marzo del 2000 www.diariodecolima.com $4.00 Un Hampón Muere También en el Tiroteo; Policíal de VA Impide Plagio; un Agente Muerto GuillermoIban Brun a Ramos,Secuestrar Carlos Salazar Preciado,a Cinco Guillermo Empresarios Saucedo del la Torre, Rafael Pineda Mendoza y Manuel Sánchez de la Madrid,l escaparon al atentado Una patrulla de Villa de Alvarez interceptó a los delincuentes l En la balacera muere el policía preventivo Juliánl Paz Rocha; herido Germán Vega Velasco El plagiario muerto quedó en un canal de riego Ell resto huyó; hasta anoche permanecían cercados por la policía en un predio de El Espinal Se espera capturarlos hoy Sergio URIBE ALVARADO Un enfrentamiento a balazos entre policías y se- de cada bando, así como otro policía herido. Los hechos cuestradores que pretendían plagiar a cinco empresarios ocurrieron ayer como a las 18:30 horas, en la vecina ciudad locales la tarde de ayer, dejó como saldo dos muertos, uno conurbada de Villa de Alvarez. Según los datos proporcionados anoche por el pro- curador de justicia del estado, Jesús Antonio Sam López, alrededor de la hora citada, en la carretera a Villa de Alvarez- Minatitlán, cerca de la empacadora de pepino de la empresa Brun Foods, varios individuos intentaron secuestrar a los señores Manuel Sánchez de la Madrid, Carlos Salazar Preciado, Guillermo Saucedo de la Torre, Rafael Pineda Mendoza y Guillermo Brun Ramos, quienes se dirigían a Esta camioneta policiaca de Villa de Alvarez.
    [Show full text]