Solutions of EGMO 2020
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

PYTHAGORAS in LONDON Mathematics ESO 2
PYTHAGORASPYTHAGORAS inin LONDONLONDON GuiaGuia dede treballtreball Laura, 2103. Jaume Plensa MaterialMaterial elaboratelaborat perper www.mat3.cat Maite Gorriz i Santi Vilches PYTHAGORAS in LONDON Mathematics ESO www.mat3.cat 2 AVATAR An Avatar is a personal icon in a virtual context. We will develop the capacity to program and control the avatar’s movements and we will learn how to use a powerful mathematics tool which is necessary to program an avatar. A. SPECIAL EQUATIONS A.1. Calculate without calculator and memorize the following results: a) 2², 3², 4², 5², 6², 7², 8², 9², 10², 11², 12², 13² i 14² b) √1 , √4 , √9 , √16 , √25 , √36 , √49 , √64 , √81 … A.2. Solve the following quadratic equations: a) x² = 64 b) x² – 6 = 30 c) 10 – x² = 9 d) x² = 2 e) 7² + x² = 2 f) 12 = 1,3 + x² g) 11² + x² = 13² B. A LITTLE BIT OF VOCABULARY AND BASIC CONCEPTS B.1.We need to learn specific vocabulary. Write the definitions of the following words and draw an illustrative picture. a) Equilateral triangle b) Isosceles triangle c) Escalene triangle d) Obtuse triangle e) Rectangle triangle or right triangle f) Acutangle triangle g) Hypotenuse h) Cathetus PYTHAGORAS in LONDON Mathematics ESO www.mat3.cat 3 B.2. Remember that we measure the angles from the horizontal side to the other one in the counterclockwise. Remember also that one turn is 360º (degrees). A Write the measure of each angle: B.3. Try to do the same figure in the Geogebra and add the exercise in the Moodle. (surname_B3_angles_2X.ggb) B.4. -

Metallic Means : Beyond the Golden Ratio, New Mathematics And
Journal of Advances in Mathematics Vol 20 (2021) ISSN: 2347-1921 https://rajpub.com/index.php/jam DOI: https://doi.org/10.24297/jam.v20i.9056 Metallic Means : Beyond the Golden Ratio, New Mathematics and Geometry of all Metallic Ratios based upon Right Triangles, The Formation of the “Triads” of Metallic Means, And their Classical Correspondence with Pythagorean Triples and p≡1(mod 4) Primes, Also the Correlation between Metallic Numbers and the Digits 3 6 9, Triangles – Triads – Triples - & 3 6 9 Dr. Chetansing Rajput M.B.B.S. Nair Hospital (Mumbai University) India, Asst. Commissioner (Govt. of Maharashtra) Lecture Link: https://youtu.be/vBfVDaFnA2k Email: [email protected] Website: https://goldenratiorajput.com/ Abstract This paper brings together the newly discovered generalised geometry of all Metallic Means and the recently published mathematical formulae those provide the precise correlations between different Metallic Ratios. The paper also puts forward the concept of the “Triads of Metallic Means”. This work also introduces the close correspondence between Metallic Ratios and the Pythagorean Triples as well as Pythagorean Primes. Moreover, this work illustrates the intriguing relationship between Metallic Numbers and the Digits 3 6 9. Keywords: Fibonacci sequence, Pi, Phi, Pythagoras Theorem, Divine Proportion, Silver Ratio, Golden Mean, Right Triangle, Metallic Numbers, Pell Numbers, Lucas Numbers, Golden Proportion, Metallic Ratio, Metallic Triples, 3 6 9, Pythagorean Triples, Pythagorean Primes, Golden Ratio, Metallic Mean Introduction The prime objective of this work is to synergize the following couple of newly discovered aspects of Metallic Means: 1) The Generalised Geometric Construction of all Metallic Ratios: cited by Wikipedia in its page on “Metallic Mean”[1]. -

Pythagorean Theorem
4.4. Pythagorean Theorem A right triangle is a triangle containing a right angle (90°). A triangle cannot have more than one right angle, since the sum of the two right angles plus the third angle would exceed the 180° total possessed by a triangle. The side opposite the right angle is called the hypotenuse (side c in the figure below). The sides adjacent to the right angle are called legs (or catheti, singular: cathetus). hypotenuse A c b right angle = 90° C a B Math notation for right triangle The Pythagorean Theorem states that the square of a hypotenuse is equal to the sum of the squares of the other two sides. It is one of the fundamental relations in Euclidean geometry. c2 = a2 + b2 2 Ac = c B A = a2 c a a A b C 2 Ab = b Pythagorean triangle with the squares of its sides and labels Pythagorean triples are integer values of a, b, c satisfying this equation. Math 8 * 4.4. Pythagorean Theorem 1 © ontaonta.com Fall 2021 Finding the Sides of a Right Triangle Example 1: Find the hypotenuse. A c 2:8 m C 9:6 m B 2 2 2 c = a + b ðsubstitute for a and b c2 = .9:6 m/2 + .2:8 m/2 c2 = 92:16 m2 + 7:84 m2 2 2 c = 100 m ðtake the square root of each side ù ù c2 = 100 m2 ù ù ù c2 = 100 m2 c = 10 m Example 2: Find the missing side b. 5 3 b 2 2 2 2 c = a + b ðsubtract a from each side ¨ ¨ c2 * a2 = ¨a2 + b2 ¨*¨a2 2 2 2 c * a = b ðswitch sides 2 2 2 b = c * a ðsubstitute for a and c b2 = 52 * 32 2 b = 25 * 9 = 16 ðtake the square root of each side ù ù b2 = 16 b = 4 Math 8 * 4.4. -

Metallic Ratios in Primitive Pythagorean Triples : Metallic Means Embedded in Pythagorean Triangles and Other Right Triangles
Journal of Advances in Mathematics Vol 20 (2021) ISSN: 2347-1921 https://rajpub.com/index.php/jam DOI: https://doi.org/10.24297/jam.v20i.9088 Metallic Ratios in Primitive Pythagorean Triples : Metallic Means embedded in Pythagorean Triangles and other Right Triangles Dr. Chetansing Rajput M.B.B.S. Nair Hospital (Mumbai University) India, Asst. Commissioner (Govt. of Maharashtra) Email: [email protected] Website: https://goldenratiorajput.com/ Lecture Link 1 : https://youtu.be/LFW1saNOp20 Lecture Link 2 : https://youtu.be/vBfVDaFnA2k Lecture Link 3 : https://youtu.be/raosniXwRhw Lecture Link 4 : https://youtu.be/74uF4sBqYjs Lecture Link 5 : https://youtu.be/Qh2B1tMl8Bk Abstract The Primitive Pythagorean Triples are found to be the purest expressions of various Metallic Ratios. Each Metallic Mean is epitomized by one particular Pythagorean Triangle. Also, the Right Angled Triangles are found to be more “Metallic” than the Pentagons, Octagons or any other (n2+4)gons. The Primitive Pythagorean Triples, not the regular polygons, are the prototypical forms of all Metallic Means. Keywords: Metallic Mean, Pythagoras Theorem, Right Triangle, Metallic Ratio Triads, Pythagorean Triples, Golden Ratio, Pascal’s Triangle, Pythagorean Triangles, Metallic Ratio A Primitive Pythagorean Triple for each Metallic Mean (훅n) : Author’s previous paper titled “Golden Ratio” cited by the Wikipedia page on “Metallic Mean” [1] & [2], among other works mentioned in the References, have already highlighted the underlying proposition that the Metallic Means -

Relations Between Some Characteristic Lengths in a Triangle
Relations between some characteristic lengths in a triangle Wolfram Koepf and Markus Brede Keywords: Pythagorean Theorem, Altitude Theorem, Cathetus Theorems, Groebner basis, poly- nomial elimination. Abstract The paper’s aim is to note a remarkable (and apparently unknown) relation for right triangles, its generalization to arbitrary triangles and the possibility to derive these and some related re- lations by elimination using Groebner basis computations with a modern computer algebra sys- tem. 1 The Pythagorean group of theorems We start by noting the Pythagorean group of theorems. Assume a right triangle T with vertices A, B and C in standard notation is given. Hence the right angle of T is at the vertex C, aBC= and bAC= denote the lengths of the two catheti and cAB= denotes the length of the hypotenuse.1 Figure 1: The standard notation in a right triangle Furthermore, the length of the altitude CH with the hypotenuse as base is denoted by h. Finally by qAH= and p = HB we denote the lengths of the hypotenuse sections. Of course by construction the equation cpq=+ is valid. The Pythagorean theorem is given in the whole triangle ACB as abc22+ = 2 as well as in the two smaller right angled triangles AHC and BHC as 1 There seems to be no worldwide standard terminology. We will use this terminology throughout the paper. 1 p22+ ha= 2 and qhb22+ = 2 respectively. Furthermore, the following well-known identities are valid in the triangle T: • (Area Identity) The double area of T can be computed as ab and as ch, hence ab = ch. -

Pythagorean Theorem
4.4. Pythagorean Theorem A right triangle is a triangle containing a right angle (90°). A triangle cannot have more than one right angle, since the sum of the two right angles plus the third angle would exceed the 180° total possessed by a triangle. The side opposite the right angle is called the hypotenuse (side c in the figure below). The sides adjacent to the right angle are called legs (or catheti, singular: cathetus). hypotenuse A c b right angle = 90° C a B Math notation for right triangle The Pythagorean Theorem states that the square of a hypotenuse is equal to the sum of the squares of the other two sides. It is one of the fundamental relations in Euclidean geometry. c2 = a2 + b2 2 Ac = c B A = a2 c a a A b C 2 Ab = b Pythagorean triangle with the squares of its sides and labels Pythagorean triples are integer values of a, b, c satisfying this equation. Math 8 * 4.4. Pythagorean Theorem 1 © ontaonta.com Fall 2021 Finding the Sides of a Right Triangle Example 1: Find the hypotenuse. A c 2:8 m C 9:6 m B 2 2 2 c = a + b ðsubstitute for a and b c2 = .9:6 m/2 + .2:8 m/2 c2 = 92:16 m2 + 7:84 m2 2 2 c = 100 m ðtake the square root of each side ù ù c2 = 100 m2 ù ù ù c2 = 100 m2 c = 10 m Example 2: Find the missing side b. 5 3 b 2 2 2 2 c = a + b ðsubtract a from each side ¨ ¨ c2 * a2 = ¨a2 + b2 ¨*¨a2 2 2 2 c * a = b ðswitch sides 2 2 2 b = c * a ðsubstitute for a and c b2 = 52 * 32 2 b = 25 * 9 = 16 ðtake the square root of each side ù ù b2 = 16 b = 4 Math 8 * 4.4. -

A Music and Mathematics
A Music and mathematics This appendix covers a topic that is underestimated in its significance by many mathematicians, who do not realize that essential aspects of music are based on applied mathematics. This short treatise is meant to show the fundamentals. It may even pique interest in the laws that govern the sen- suous beauty of music. Additional literature is provided for readers who are particularly interested in this topic. The mathematical proportions of a sounding string were first defined by Py- thagoras, who made his discoveries by subdividing tense strings. This chapter describes changes in scales and tonal systems over the course of musical his- tory. The author of this appendix is Reinhard Amon, a musician and the author of a lexicon on major-minor harmonic systems. The chapter will conclude with exercises in “musical calculation” that show the proximity between music and mathematics. © Springer International Publishing AG 2017 G. Glaeser, Math Tools, https://doi.org/10.1007/978-3-319-66960-1 502 Chapter A: Music and mathematics A.1 Basic approach, fundamentals of natural science The basic building blocks of music are rhythmic structures, certain pitches, and their distances (= intervals). Certain intervals are preferred by average listeners, such as the octave and the fifth. Others tend to be rejected or ex- cluded. If one makes an experimentally-scientific attempt to create a system of such preferred and rejected intervals, one will find a broad correspondence between the preferences of the human ear and the overtone series, which fol- lows from natural laws. Thus, there exists a broad correspondence between quantity (mathematical proportion) and quality (human value judgement). -
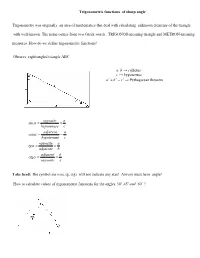
Trigonometric Functions of Sharp Angle
Trigonometric functions of sharp angle Trigonometry was originally an area of mathematics that deal with calculating unknown elements of the triangle with well-known. The name comes from two Greek words , TRIGONOS-meaning triangle and METRON-meaning measures. How do we define trigonometric functions? Observe right-angled triangle ABC. a, b → cathetus c → hypotenuse a2 + b2 = c2 → Pythagorean theorem opposite a sinα = = hypotenuse c adjacent a cosα = = hypotenuse c opposite a tgα = = adjacent b adjacent b ctgα = = opposite a Take heed: The symbol sin (cos, tg, ctg) will not indicate any size! Always must have angle! How to calculate values of trigonometric functions for the angles 30o ,45o and 60o ? a opposite a 1 sin 30o = = 2 = = hypotenuse a 2a 2 a 3 adjacent 3 cos30o = = 2 = hypotenuse a 2 a opposite 1 1 3 3 tg30o = = 2 = = ⋅ = adjacent 3 3 3 3 3 2 a 3 adjacent ctg30o = = 2 = 3 opposite a 2 Now we'll do (by definition) for angle 60o : a 3 3 sin 60o = 2 = a 2 a 1 cos60o = 2 = a 2 3 3 tg60o = 2 = a 3 2 a 3 ctg60o = 2 = a 3 3 2 For the value of the trigonometric functions of angle 45o , we will use half of the square. opposite a 1 2 2 sin 45o = = = ⋅ = hypotenuse a 2 2 2 2 adjacent a 2 cos 45o = = = hypotenuse 2 a 2 opposite a tg45o = = = 1 adjacent a adjacent a ctg45o = = = 1 opposite a In this way we get table: 30o 45o 60o sinα 1 2 3 2 2 2 cosα 3 2 1 2 2 2 tgα 3 1 3 3 ctgα 3 1 3 3 Of course, we will table later expand to all corners from0o → 360o . -

Pythagoras and the Creation of Knowledge
Open Journal of Philosophy 2014. Vol.4, No.1, 68-74 Published Online February 2014 in SciRes (http://www.scirp.org/journal/ojpp) http://dx.doi.org/10.4236/ojpp.2014.41010 Pythagoras and the Creation of Knowledge Jose R. Parada-Daza1, Miguel I. Parada-Contzen2 1Universidad de Concepcion, Concepcion, Chile 2Technische Universität Berlin, Berlin, Germany Email: [email protected], [email protected] Received December 30th, 2013; revised January 30th, 2014; accepted February 7th, 2014 Copyright © 2014 Jose R. Parada-Daza, Miguel I. Parada-Contzen. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribu- tion License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Jose R. Parada-Daza, Miguel I. Parada-Contzen. All Copyright © 2014 are guarded by law and by SCIRP as a guardian. In this paper, an approach to Pythagoras’ Theorem is presented within the historical context in which it was developed and from the underlying intellectual outline of the Pythagorean School. This was analyzed from a rationalism standpoint. An experiment is presented to the reader so that they, through direct ob- servation, can analyze Pythagoras’ Theorem and its relation to the creation of knowledge. The theory of knowledge conceptualization is used. Keywords: Theorem; Pythagoras; Rationalism; Empiricism; Knowledge Introduction observation analysis, even though ideas for discussion are crea- ted by the authors. This paper discusses the creation of scientific knowledge and The historical development of Pythagoras and the Pythago- focuses primarily on the Pythagorean Theorem, which is an un- rean School is outlined within this paper and the different un- questioning development from rationalism. -

Math10th Grade LEARNING OBJECT Identifying Properties of Triangles
Math10th grade LEARNING OBJECT LEARNING UNIT Trigonometry, a study of Identifying properties of triangles the measurement of the angle through function S/K SCO: Understand the isosceles triangle theorem. SKILL 1. Identify triangles with sides of equal measurement. SKILL 2. Identify triangles with equal angles. SKILL 3. Distinguish the metric characteristics of isosceles right triangles. SKILL 4. Understand the hypothesis stated in the isosceles triangle theorem and its inverse. SKILL 5. Solve geometric situations by applying the isosceles right triangle theorem. SCO: Identify the 30-60-90 theorem. SKILL 6. Understand the relationship of constant ratio between the hypotenuse and a leg. SKILL 7. Identify the relationships of measurement between the angles and catheti of the triangle. SKILL 8. Illustrate 30-60-90 triangles by applying the relationship between the measurements between the catheti. SCO: Understand the Pythagorean Theorem. SKILL 9. Recognize the hypotenuse as the longest leg in a right triangle. SKILL 10. Interpret the Pythagorean Theorem in problem solutions. SKILL 11. Solve measurement situations involving right triangles. SKILL 12. Make an argument supporting the use of the procedure in problem solving. Language English Socio cultural context of 10th grade students will find situations in their the LO context related with the measurement of heights and lengths of sides of physical structures related to construction, such as pyramids, towers, ramps and others. Curricular axis Variational thinking and analytic and algebraic systems. Spatial thinking and geometric systems. Standard competencies Recognize and contrast properties and geometric relationships used to demonstrate basic theorems. Background Knowledge Interpretation of situations by means of the Pythagorean Theorem. -

A Balloon-Borne Cosmic Microwave Background Anisotropy Probe
The E and B EXperiment: A balloon-borne cosmic microwave background anisotropy probe Seth Hillbrand Submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the Graduate School of Arts and Sciences COLUMBIA UNIVERSITY 2014 c 2014 Seth Hillbrand All Rights Reserved ABSTRACT The E and B EXperiment: A balloon-borne cosmic microwave background anisotropy probe Seth Hillbrand The E and B Experiment (EBEX), is a balloon-borne sub-orbital cosmic microwave background polarimeter, designed to measure polarization levels in the microwave spectrum. EBEX recently completed an 11-day Antarctic long duration balloon (LDB) science flight in January, 2013. 1000 transition edge sensor bolometric detectors in ∼ three frequency bands centered at 150, 250 and 410 GHz sampled a large segment of the southern sky. Over 1.5TB of data were collected during the LDB flight. In this thesis, we describe the design and performance of the EBEX software components monitoring and controlling the system during the flight, including automation, telemetry, data storage and readout array management. We also describe the design and development of a novel attitude reconstruction system for a balloon-borne pointed observation platform based on a daytime star camera and 3-axis gyroscopes. The data gathered during the LDB flight are analyzed and the results presented showing attitude reconstruction error at less than 2000 RMS for an 80 second interval. Table of Contents 1 Introduction1 2 EBEX Science4 2.1 Concordance Cosmology.........................4 2.1.1 Expanding Universe.......................6 2.1.2 Flat Universe...........................9 2.1.3 Hot, Dense Early Universe....................9 2.1.4 Dark Matter Universe..................... -

2 Introductory Problems
Three parabolas Solutions F.Nilov, A.Zaslavsky 2 Introductory problems 1. Let X′ be the projection of X to the directrix. Then FX = XX′. Suppose that the bisectrix l of the angle X′XF isn’t the tangent to parabola. Then l intersect the parabola in some point Y , distinct from X. Note that the triangles FXY and X′XY are equal and so FY = YX′. Let Y ′ be the projection of Y to the directrix. Then YY ′ = FY = YX′. But it is impossible because YY ′ and YX′ are the hypothenuse and the cathetus of rectangle triangle YX′Y ′. 2. Let l touche the parabola in the point X. Then FX = XX′. By problem 1 l is the bisectrix of isosceles triangle FXX′. So l is the medial perpendicular to the segment FX′, and the points X′ and F are symmetric wrt l. 3. By problem 2 the lines PX and PY are medial perpendiculars of segments FX′ и FY ′. So their common point P is the circumcenter of FX′Y ′. 4. Consider the medial line of the trapezoid XX′Y ′Y . It is perpendicular to the directrix and so parallel to the axis of the parabola. Also it is the median of PXY , because it pass through the midpoint of segment XY and (by problem 3) through P . 5. Consider the line l passing through P and parallel to the axis of the parabola. We must prove that the angle φ between l and PX is equal to the angle FPY . Let X′′ and Y ′′ be the projections of F to the lines PX and PY .