DOCSLIB.ORG

Stellar Structure and Evolution: Syllabus 3.3 the Virial Theorem and Its Implications (ZG: P5-2; CO: 2.4) Ph

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Stellar Structure and Evolution: Syllabus 3.3 the Virial Theorem and Its Implications (ZG: P5-2; CO: 2.4) Ph Page 2 Stellar Structure and Evolution: Syllabus 3.3 The Virial Theorem and its Implications (ZG: P5-2; CO: 2.4) Ph. Podsiadlowski (MT 2006) 3.4 The Energy Equation and Stellar Timescales (CO: 10.3) (DWB 702, (2)73343, [email protected]) (www-astro.physics.ox.ac.uk/˜podsi/lec mm03.html) 3.5 Energy Transport by Radiation (ZG: P5-10, 16-1) and Con- vection (ZG: 16-1; CO: 9.3, 10.4) Primary Textbooks 4. The Equations of Stellar Structure (ZG: 16; CO: 10) ZG: Zeilik & Gregory, “Introductory Astronomy & Astro- • 4.1 The Mathematical Problem (ZG: 16-2; CO: 10.5) physics” (4th edition) 4.1.1 The Vogt-Russell “Theorem” (CO: 10.5) CO: Carroll & Ostlie, “An Introduction to Modern Astro- • 4.1.2 Stellar Evolution physics” (Addison-Wesley) 4.1.3 Convective Regions (ZG: 16-1; CO: 10.4) also: Prialnik, “An Introduction to the Theory of Stellar Struc- • 4.2 The Equation of State ture and Evolution” 4.2.1 Perfect Gas and Radiation Pressure (ZG: 16-1: CO: 1. Observable Properties of Stars (ZG: Chapters 11, 12, 13; CO: 10.2) Chapters 3, 7, 8, 9) 4.2.2 Electron Degeneracy (ZG: 17-1; CO: 15.3) 1.1 Luminosity, Parallax (ZG: 11; CO: 3.1) 4.3 Opacity (ZG: 10-2; CO: 9.2) 1.2 The Magnitude System (ZG: 11; CO: 3.2, 3.6) 5. Nuclear Reactions (ZG: P5-7 to P5-9, P5-12, 16-1D; CO: 10.3) 1.3 Black-Body Temperature (ZG: 8-6; CO: 3.4) 5.1 Nuclear Reaction Rates (ZG: P5-7) 1.4 Spectral Classification, Luminosity Classes (ZG: 13-2/3; CO: 5.2 Hydrogen Burning 5.1, 8.1, 8.3) 5.2.1 The pp Chain (ZG: P5-7, 16-1D) 1.5 Stellar Atmospheres (ZG: 13-1; CO: 9.1, 9.4) 5.2.2 The CN Cycle (ZG: P5-9; 16-1D) 1.6 Stellar Masses (ZG: 12-2/3; CO: 7.2, 7.3) 5.3 Energy Generation from H Burning (CO: 10.3) 1.7 Stellar Radii (ZG: 12-4/5; CO: 7.3) 5.4 Other Reactions Involving Light Elements (Supplementary) 2. Correlations between Stellar Properties (ZG: Chapters 12, 13, 5.5 Helium Burning (ZG: P5-12; 16-1D) 14; CO: Chapters 7, 8, 13) 6. The Evolution of Stars 2.1 Mass-Luminosity Relations (ZG: 12-2; CO: 7.3) 6.1 The Structure of Main-Sequence Stars (ZG: 16-2; CO 10.6, 2.2 Hertzsprung-Russell diagrams and Colour-Magnitude Dia- 13.1) grams (ZG: 13-3; CO: 8.2) 6.2 The Evolution of Low-Mass Stars (ZG: 16-3; CO: 13.2) 2.3 Globular Clusters and Open (Galactic) Clusters (ZG:13-3, 14-2; OG: 13.4) 6.2.1 The Pre-Main Sequence Phase 6.2.2 The Core Hydrogen-Burning Phase 2.4 Chemical Composition (ZG: 13-3; CO: 9.4) 6.2.3 The Red-Giant Phase 2.5 Stellar Populations (ZG: 14-3; CO: 13.4) 6.2.4 The Helium Flash 3. The Physical State of the Stellar Interior (ZG: P5, 16; CO: 10) 6.2.5 The Horizontal Branch 3.1 The Equation of Hydrostatic Equilibrium (ZG: 16-1; CO: 6.2.6 The Asymptotic Giant Branch 10.1) 6.2.7 White Dwarfs and the Chandrasekhar Mass (ZG: 17-1; CO: 13.2) 3.2 The Dynamical Timescale (ZG: P5-4; CO: 10.4) Page 4 Useful Numbers Astronomical unit AU = 1.5 1011 m × Parsec pc = 3.26 ly =3.086 1016 m 6.3 The Evolution of Massive Stars (CO: 13.3) × Lightyear ly = 9.46 1015 m 6.4 Supernovae (ZG: 18-5B/C/D) × Mass of Sun M =1.99 1030 kg ⊙ × 6.4.1 Explosion Mechanisms Mass of Earth M =5.98 1024 kg ⊕ × 6 6.4.2 Supernova Classification =3 10− M × 3 ⊙ 6.4.3 SN 1987 A (ZG: 18-5E) Mass of Jupiter MJup =10− M ⊙ 6.4.4 Neutron Stars (ZG: 17-2; CO: 15.6) Radius of Sun R =6.96 108 m ⊙ × 6.4.5 Black Holes (ZG: 17-3; CO: 16) Radius of Earth R =6380km ⊕ 3 Radius of Jupiter RJup =10− R 7. Binary Stars (ZG: 12; CO: 7, 17) ⊙ Luminosity of Sun L =3.86 1026 W ⊙ × 7.1 Classification Effective temperature of Sun Teff =5780K 6 Central temperature of Sun Tc =15.6 10 K 7.2 The Binary Mass Function × Distance to the Galactic centre R0 =8.0kpc 7.3 The Roche Potential 1 Velocity of Sun about Galactic centre V0 =220kms− 7.4 Binary Mass Transfer Diameter of Galactic disc = 50 kpc 7.5 Interacting Binaries (Supplementary) Mass of Galaxy = 7 1011 M × ⊙ Appendices (Supplementary Material) A. Brown Dwarfs (ZG: 17-1E) B. Planets (ZG: 7-6; CO: 18.1) C. The Structure of the Sun and The Solar Neutrino Problem (ZG: P5-11, 10, 16-1D; CO: 11.1) D. Star Formation (ZG: 15.3; CO: 12) E. Gamma-Ray Bursts (ZG: 16-6; CO: 25.4) Page 6 Summary of Equations Opacity: Thomson (Electron) Scattering: Equation of Stellar Structure 2 1 κ =0.020 m kg− (1 + X)(page69) Equation of Hydrostatic Equilibrium: Kramer’s Opacity: dPr GMrρr 3.5 = (page 45) κ ρ T − (page 69) dr − r2 ∝ Low-Temperature Opacity: Equation of Mass Conservation: κ ρ1/2 T 4 (page 69) dMr 2 ∝ =4πr ρr (page 45) dr Energy Generation Rates (Rough!) Energy Conservation (no gravitational energy): PP Burning: 2 4 dL εPP ρ XH T (page 79) r =4πr2ρ ε (page 52) ∝ dr r r CNO Burning: 20 Energy Transport (Radiative Diffusion Equation): ε ρ XH XCNO T (page 79) CNO ∝ 4ac dT L = 4πr2 T 3 (page 55) Helium Burning (triple α): r − 3κρ dr 3 2 30 ε3 X ρ T (page 82) Energy Transport by Convection, Convective Stability: α ∝ He dT γ 1 T dP Stellar Timescales = − (page 57) dr γ P dr Dynamical Timescale: 1 Constitutive Relations tdyn (page 48) ≃ √4Gρ Equation of State, Ideal Gas: 3 1/2 30 min ρ/1000 kg m− − ρ ∼ P = NkT = kT (page 65) # $ µmH Thermal (Kelvin-Helmholtz) Timescale): Equation of State, Radiation Pressure: GM 2 tKH (page 51) ≃ 2RL 1 4 P = aT (page 66) 7 2 1 1 3 1.5 10 yr (M/M ) (R/R )− (L/L )− ∼ × ⊙ ⊙ ⊙ Equation of State, Electron Degeneracy (T =0K): Nuclear Timescale: 5/3 2 ρ tnuc Mc/M η (Mc )/L (page 52) P = K1 (page 66) ≃ !µemH " 10 3 10 yr (M/M )− (non-relativistic degeneracy) ∼ ⊙ (Radiative) Diffusion Timescale: ρ 4/3 P = K2 (page 67) l R2 ! " s µemH tdiff = N (page 53) × c ≃ lc (relativistic degeneracy) Notes: Notes: Page 8 Derived Relations Central Temperature Relation (for Ideal Gas): Miscellaneous Equations Distance Modulus: GMs µmH kTc (page 46) ≃ Rs (m M) =5log(D/10pc) (page 12) − V Virial Theorem: Absolute V Magnitude: 3(γ 1)U + Ω =0 (page50) − MV = 2.5logL/L +4.72 + B.C. + AV (page 12) Mass–Luminosity Relation (for stars 1 M ): − ⊙ ∼ ⊙ 4 Salpeter Initial Mass Function (IMF): M L L (page 85) ! " 2.35 ≃ ⊙ M f(M)dM M − dM (page 15) ⊙ ∝ Mass–MS Lifetime Relation (for stars 1 M ): ∼ ⊙ Black-Body Relation: 2 4 3 L =4π R σTeff (page 17) 10 M − s TMS 10 yr (page 85) ≃ ! M " Kepler’s Law: ⊙ 2 3 2π Mass–Radius Relation for White Dwarfs (non-relativistic): a = G(M1 + M2)(page25) ! P " 1 5/3 1/3 Notes: R (µemH) M − (page 98) ∝ me Chandrasekhar Mass for White Dwarfs: 2 2 MCh =1.457 M (page 99) !µe " ⊙ Schwarzschild Radius (Event Horizon) for Black Holes: 2GM M RS = 3km (page 112) c2 ≃ !M " ⊙ Notes: Page 10 STELLAR STRUCTURE AND EVOLUTION 1.1 LUMINOSITY (ZG: 11; CO: 3.1) 1. OBSERVABLE PROPERTIES OF STARS (‘power’, [J/s=W]) Basic large-scale observable properties: ∞ 2 ∞ Ls = L d = 4 Rs F d Luminosity %0 %0 Surface temperature where F is the radiative flux at wavelength at the stellar surface, Radius R the stellar radius. Energy may also be lost in the form of Mass s neutrinos or by direct mass loss (generally unobservable). Further observable: Astronomers measure: Spectrum ... yields information about surface chemical composition and gravity 2 f =(Rs/D) F at Earth’s surface Evidence from: To obtain L we must know the star’s distance D and correct • Individual stars for: • Binary systems ◃ absorption in the Earth’s atmosphere (standard • methods) Star clusters....these reveal how stars evolve with time • ◃ absorption in interstellar space (negligible for nearby stars) Nuclear physics...energy source, synthesis of heavy elements • Measurements from the Hipparcos satellite (1989–1993) have • No direct information about physical conditions in stellar interiors yielded parallaxes accurate to 0.002 arcsec for about 100,000 (except from helioseismology and stars. The largest stellar parallax (Proxima Centauri) is 0.765 solar neutrinos) arcsec. No direct evidence for stellar evolution......typical timescale 106 109 − Notes: years.......(except for a few very unusual stars and supernovae) Notes: Page 12 THE UBV SYSTEM the UBV system (ultraviolet, blue, visual) which can be extended 1.2 STELLAR MAGNITUDES (ZG: 11; CO: 3.2, 3.6) • into the red, infrared (RI) measure stellar flux (i.e. f = L/4 D2, L: luminosity, D: distance) • 26 3 2 ◃ for Sun: L = 3.86 10 W, f = 1.360 10 Wm− (solar ⊙ × × constant) ◃ luminosity measurement requires distance determination (1A.U. = 1.50 1011 m) × define apparent magnitudes of two stars, m1,m2,by • m1 m2 = 2.5logf2/f1 − zero point: Vega (historical) m = 26.82 • → ⊙ − to measure luminosity define absolute magnitude M to be the • approximate notation for magnitudes apparent magnitude of the object if it were at a distance 10 pc region apparent absolute solar value (1 pc = 3.26 light years = 3.09 1016 m) × ultraviolet U or mU MU 5.61 define bolometric magnitude as the absolute magnitude corre- • sponding to the luminosity integrated over all wavebands; for blue B or mB MB 5.48 the Sun Mbol = 4.72 visual V or mV MV 4.83 ⊙ (near yellow) in practice, the total luminosity is difficult to measure because • of atmospheric absorption and limited detector response colours (colour indices): relative magnitudes in different wave- define magnitudes over limited wavelength bands • • length bands, most commonly used: B V, U B − − Notes: define bolometric correction: B.C.
Load more

Recommended publications
  • Lurking in the Shadows: Wide-Separation Gas Giants As Tracers of Planet Formation
    Lurking in the Shadows: Wide-Separation Gas Giants as Tracers of Planet Formation Thesis by Marta Levesque Bryan In Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy CALIFORNIA INSTITUTE OF TECHNOLOGY Pasadena, California 2018 Defended May 1, 2018 ii © 2018 Marta Levesque Bryan ORCID: [0000-0002-6076-5967] All rights reserved iii ACKNOWLEDGEMENTS First and foremost I would like to thank Heather Knutson, who I had the great privilege of working with as my thesis advisor. Her encouragement, guidance, and perspective helped me navigate many a challenging problem, and my conversations with her were a consistent source of positivity and learning throughout my time at Caltech. I leave graduate school a better scientist and person for having her as a role model. Heather fostered a wonderfully positive and supportive environment for her students, giving us the space to explore and grow - I could not have asked for a better advisor or research experience. I would also like to thank Konstantin Batygin for enthusiastic and illuminating discussions that always left me more excited to explore the result at hand. Thank you as well to Dimitri Mawet for providing both expertise and contagious optimism for some of my latest direct imaging endeavors. Thank you to the rest of my thesis committee, namely Geoff Blake, Evan Kirby, and Chuck Steidel for their support, helpful conversations, and insightful questions. I am grateful to have had the opportunity to collaborate with Brendan Bowler. His talk at Caltech my second year of graduate school introduced me to an unexpected population of massive wide-separation planetary-mass companions, and lead to a long-running collaboration from which several of my thesis projects were born.
    [Show full text]
  • This Work Is Protected by Copyright and Other Intellectual Property Rights
    This work is protected by copyright and other intellectual property rights and duplication or sale of all or part is not permitted, except that material may be duplicated by you for research, private study, criticism/review or educational purposes. Electronic or print copies are for your own personal, non- commercial use and shall not be passed to any other individual. No quotation may be published without proper acknowledgement. For any other use, or to quote extensively from the work, permission must be obtained from the copyright holder/s. Fundamental properties of M-dwarfs in eclipsing binary star systems Samuel Gill Doctor of Philosophy Department of Physics, Keele University March 2019 i Abstract The absolute parameters of M-dwarfs in eclipsing binary systems provide important tests for evolutionary models. Those that have been measured reveal significant discrepancies with evolutionary models. There are two problems with M-dwarfs: 1. M-dwarfs generally appear bigger and cooler than models predict (such that their luminosity agrees with models) and 2. some M-dwarfs in eclipsing binaries are measured to be hotter than expected for their mass. The exact cause of this is unclear and a variety of conjectures have been put forward including enhanced magnetic activity and spotted surfaces. There is a lack of M-dwarfs with absolute parameters and so the exact causes of these disparities are unclear. As the interest in low-mass stars rises from the ever increasing number of exoplanets found around them, it is important that a considerable effort is made to understand why this is so. A solution to the problem lies with low-mass eclipsing binary systems discovered by the WASP (Wide Angle Search for Planets) project.
    [Show full text]
  • Temperature-Spectral Class-Color Index Relationships for Main
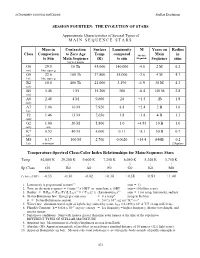
    ASTRONOMY SURVIVAL NOTEBOOK Stellar Evolution SESSION FOURTEEN: THE EVOLUTION OF STARS Approximate Characteristics of Several Types of MAIN SEQUENCE STARS Mass in Contraction Surface Luminosity M Years on Radius Class Comparison to Zero Age Temp. compared Absolute Main in to Sun Main Sequence (K) to sun Magnitude Sequence suns Not well known O6 29.5 10 Th 45,000 140,000 -4.0 2 M 6.2 mid blue super g O9 22.6 100 Th 37,800 55,000 -3.6 4 M 4.7 late blue super g B2 10.0 400 Th 21,000 3,190 -1.9 30 M 4.3 early B5 5.46 1 M 15,200 380 -0.4 140 M 2.8 mid A0 2.48 4 M 9,600 24 +1.5 1B 1.8 early A7 1.86 10 M 7,920 8.8 +2.4 2 B 1.6 late F2 1.46 15 M 7,050 3.8 +3.8 4 B 1.3 early G2 1.00 20 M 5,800 1.0 +4.83 10 B 1.0 early sun K7 0.53 40 M 4,000 0.11 +8.1 50 B 0.7 late M8 0.17 100 M 2,700 0.0020 +14.4 840B 0.2 late minimum 2 Jupiters Temperature-Spectral Class-Color Index Relationships for Main-Sequence Stars Temp 54,000 K 29,200 K 9,600 K 7,350 K 6,050 K 5,240 K 3,750 K | | | | | | | Sp Class O5 B0 A0 F0 G0 K0 M0 Co Index (UBV) -0.33 -0.30 -0.02 +0.30 +0.58 +0.81 +1.40 1.
    [Show full text]
  • Exoplanet.Eu Catalog Page 1 # Name Mass Star Name
    exoplanet.eu_catalog # name mass star_name star_distance star_mass OGLE-2016-BLG-1469L b 13.6 OGLE-2016-BLG-1469L 4500.0 0.048 11 Com b 19.4 11 Com 110.6 2.7 11 Oph b 21 11 Oph 145.0 0.0162 11 UMi b 10.5 11 UMi 119.5 1.8 14 And b 5.33 14 And 76.4 2.2 14 Her b 4.64 14 Her 18.1 0.9 16 Cyg B b 1.68 16 Cyg B 21.4 1.01 18 Del b 10.3 18 Del 73.1 2.3 1RXS 1609 b 14 1RXS1609 145.0 0.73 1SWASP J1407 b 20 1SWASP J1407 133.0 0.9 24 Sex b 1.99 24 Sex 74.8 1.54 24 Sex c 0.86 24 Sex 74.8 1.54 2M 0103-55 (AB) b 13 2M 0103-55 (AB) 47.2 0.4 2M 0122-24 b 20 2M 0122-24 36.0 0.4 2M 0219-39 b 13.9 2M 0219-39 39.4 0.11 2M 0441+23 b 7.5 2M 0441+23 140.0 0.02 2M 0746+20 b 30 2M 0746+20 12.2 0.12 2M 1207-39 24 2M 1207-39 52.4 0.025 2M 1207-39 b 4 2M 1207-39 52.4 0.025 2M 1938+46 b 1.9 2M 1938+46 0.6 2M 2140+16 b 20 2M 2140+16 25.0 0.08 2M 2206-20 b 30 2M 2206-20 26.7 0.13 2M 2236+4751 b 12.5 2M 2236+4751 63.0 0.6 2M J2126-81 b 13.3 TYC 9486-927-1 24.8 0.4 2MASS J11193254 AB 3.7 2MASS J11193254 AB 2MASS J1450-7841 A 40 2MASS J1450-7841 A 75.0 0.04 2MASS J1450-7841 B 40 2MASS J1450-7841 B 75.0 0.04 2MASS J2250+2325 b 30 2MASS J2250+2325 41.5 30 Ari B b 9.88 30 Ari B 39.4 1.22 38 Vir b 4.51 38 Vir 1.18 4 Uma b 7.1 4 Uma 78.5 1.234 42 Dra b 3.88 42 Dra 97.3 0.98 47 Uma b 2.53 47 Uma 14.0 1.03 47 Uma c 0.54 47 Uma 14.0 1.03 47 Uma d 1.64 47 Uma 14.0 1.03 51 Eri b 9.1 51 Eri 29.4 1.75 51 Peg b 0.47 51 Peg 14.7 1.11 55 Cnc b 0.84 55 Cnc 12.3 0.905 55 Cnc c 0.1784 55 Cnc 12.3 0.905 55 Cnc d 3.86 55 Cnc 12.3 0.905 55 Cnc e 0.02547 55 Cnc 12.3 0.905 55 Cnc f 0.1479 55
    [Show full text]
  • Vita Extraterrestre Sugli Esopianeti Nella Via Lattea
    Vita extraterrestre sugli esopianeti nella Via Lattea Maria Cristina De Liso Liceo Cantonale di Locarno 2014-2015 Professori responsabili: Gianni Boffa e Christian Ferrari Indice 1 Premessa ...................................................................................................................................... 4 2 Introduzione ................................................................................................................................ 4 3 Origine dell’astronomia .............................................................................................................. 5 4 Verso il Sistema Solare e oltre ................................................................................................... 7 4.1 Il Sistema Solare .................................................................................................................. 8 4.2 Le leggi di Keplero ............................................................................................................ 10 4.3 Le comete ........................................................................................................................... 13 4.3.1 Origine ............................................................................................................................ 14 4.3.2 Classificazione e traiettoria orbitale ............................................................................ 15 4.3.3 Breve storia delle scoperte ............................................................................................ 16
    [Show full text]
  • GTO Keypad Manual, V5.001
    ASTRO-PHYSICS GTO KEYPAD Version v5.xxx Please read the manual even if you are familiar with previous keypad versions Flash RAM Updates Keypad Java updates can be accomplished through the Internet. Check our web site www.astro-physics.com/software-updates/ November 11, 2020 ASTRO-PHYSICS KEYPAD MANUAL FOR MACH2GTO Version 5.xxx November 11, 2020 ABOUT THIS MANUAL 4 REQUIREMENTS 5 What Mount Control Box Do I Need? 5 Can I Upgrade My Present Keypad? 5 GTO KEYPAD 6 Layout and Buttons of the Keypad 6 Vacuum Fluorescent Display 6 N-S-E-W Directional Buttons 6 STOP Button 6 <PREV and NEXT> Buttons 7 Number Buttons 7 GOTO Button 7 ± Button 7 MENU / ESC Button 7 RECAL and NEXT> Buttons Pressed Simultaneously 7 ENT Button 7 Retractable Hanger 7 Keypad Protector 8 Keypad Care and Warranty 8 Warranty 8 Keypad Battery for 512K Memory Boards 8 Cleaning Red Keypad Display 8 Temperature Ratings 8 Environmental Recommendation 8 GETTING STARTED – DO THIS AT HOME, IF POSSIBLE 9 Set Up your Mount and Cable Connections 9 Gather Basic Information 9 Enter Your Location, Time and Date 9 Set Up Your Mount in the Field 10 Polar Alignment 10 Mach2GTO Daytime Alignment Routine 10 KEYPAD START UP SEQUENCE FOR NEW SETUPS OR SETUP IN NEW LOCATION 11 Assemble Your Mount 11 Startup Sequence 11 Location 11 Select Existing Location 11 Set Up New Location 11 Date and Time 12 Additional Information 12 KEYPAD START UP SEQUENCE FOR MOUNTS USED AT THE SAME LOCATION WITHOUT A COMPUTER 13 KEYPAD START UP SEQUENCE FOR COMPUTER CONTROLLED MOUNTS 14 1 OBJECTS MENU – HAVE SOME FUN!
    [Show full text]
  • FY13 High-Level Deliverables
    National Optical Astronomy Observatory Fiscal Year Annual Report for FY 2013 (1 October 2012 – 30 September 2013) Submitted to the National Science Foundation Pursuant to Cooperative Support Agreement No. AST-0950945 13 December 2013 Revised 18 September 2014 Contents NOAO MISSION PROFILE .................................................................................................... 1 1 EXECUTIVE SUMMARY ................................................................................................ 2 2 NOAO ACCOMPLISHMENTS ....................................................................................... 4 2.1 Achievements ..................................................................................................... 4 2.2 Status of Vision and Goals ................................................................................. 5 2.2.1 Status of FY13 High-Level Deliverables ............................................ 5 2.2.2 FY13 Planned vs. Actual Spending and Revenues .............................. 8 2.3 Challenges and Their Impacts ............................................................................ 9 3 SCIENTIFIC ACTIVITIES AND FINDINGS .............................................................. 11 3.1 Cerro Tololo Inter-American Observatory ....................................................... 11 3.2 Kitt Peak National Observatory ....................................................................... 14 3.3 Gemini Observatory ........................................................................................
    [Show full text]
  • Exoplanet.Eu Catalog Page 1 Star Distance Star Name Star Mass
    exoplanet.eu_catalog star_distance star_name star_mass Planet name mass 1.3 Proxima Centauri 0.120 Proxima Cen b 0.004 1.3 alpha Cen B 0.934 alf Cen B b 0.004 2.3 WISE 0855-0714 WISE 0855-0714 6.000 2.6 Lalande 21185 0.460 Lalande 21185 b 0.012 3.2 eps Eridani 0.830 eps Eridani b 3.090 3.4 Ross 128 0.168 Ross 128 b 0.004 3.6 GJ 15 A 0.375 GJ 15 A b 0.017 3.6 YZ Cet 0.130 YZ Cet d 0.004 3.6 YZ Cet 0.130 YZ Cet c 0.003 3.6 YZ Cet 0.130 YZ Cet b 0.002 3.6 eps Ind A 0.762 eps Ind A b 2.710 3.7 tau Cet 0.783 tau Cet e 0.012 3.7 tau Cet 0.783 tau Cet f 0.012 3.7 tau Cet 0.783 tau Cet h 0.006 3.7 tau Cet 0.783 tau Cet g 0.006 3.8 GJ 273 0.290 GJ 273 b 0.009 3.8 GJ 273 0.290 GJ 273 c 0.004 3.9 Kapteyn's 0.281 Kapteyn's c 0.022 3.9 Kapteyn's 0.281 Kapteyn's b 0.015 4.3 Wolf 1061 0.250 Wolf 1061 d 0.024 4.3 Wolf 1061 0.250 Wolf 1061 c 0.011 4.3 Wolf 1061 0.250 Wolf 1061 b 0.006 4.5 GJ 687 0.413 GJ 687 b 0.058 4.5 GJ 674 0.350 GJ 674 b 0.040 4.7 GJ 876 0.334 GJ 876 b 1.938 4.7 GJ 876 0.334 GJ 876 c 0.856 4.7 GJ 876 0.334 GJ 876 e 0.045 4.7 GJ 876 0.334 GJ 876 d 0.022 4.9 GJ 832 0.450 GJ 832 b 0.689 4.9 GJ 832 0.450 GJ 832 c 0.016 5.9 GJ 570 ABC 0.802 GJ 570 D 42.500 6.0 SIMP0136+0933 SIMP0136+0933 12.700 6.1 HD 20794 0.813 HD 20794 e 0.015 6.1 HD 20794 0.813 HD 20794 d 0.011 6.1 HD 20794 0.813 HD 20794 b 0.009 6.2 GJ 581 0.310 GJ 581 b 0.050 6.2 GJ 581 0.310 GJ 581 c 0.017 6.2 GJ 581 0.310 GJ 581 e 0.006 6.5 GJ 625 0.300 GJ 625 b 0.010 6.6 HD 219134 HD 219134 h 0.280 6.6 HD 219134 HD 219134 e 0.200 6.6 HD 219134 HD 219134 d 0.067 6.6 HD 219134 HD
    [Show full text]
  • Relativistic Shapiro Delay Measurements of an Extremely Massive Millisecond Pulsar
    LETTERS https://doi.org/10.1038/s41550-019-0880-2 Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar H. T. Cromartie 1*, E. Fonseca 2, S. M. Ransom 3, P. B. Demorest4, Z. Arzoumanian5, H. Blumer6,7, P. R. Brook6,7, M. E. DeCesar8, T. Dolch9, J. A. Ellis10, R. D. Ferdman 11, E. C. Ferrara12,13, N. Garver-Daniels6,7, P. A. Gentile6,7, M. L. Jones6,7, M. T. Lam6,7, D. R. Lorimer6,7, R. S. Lynch14, M. A. McLaughlin6,7, C. Ng15,16, D. J. Nice 8, T. T. Pennucci 17, R. Spiewak 18, I. H. Stairs15, K. Stovall4, J. K. Swiggum19 and W. W. Zhu20 Despite its importance to our understanding of physics at Precise neutron star mass measurements are an effective way to supranuclear densities, the equation of state (EoS) of mat- constrain the EoS of the ultradense matter in neutron star interiors. ter deep within neutron stars remains poorly understood. Although radio pulsar timing cannot directly determine neutron Millisecond pulsars (MSPs) are among the most useful astro- star radii, the existence of pulsars with masses exceeding the maxi- physical objects in the Universe for testing fundamental phys- mum mass allowed by a given model can straightforwardly rule out ics, and place some of the most stringent constraints on this that EoS. high-density EoS. Pulsar timing—the process of accounting In 2010, Demorest et al. reported the discovery of a 2 M⊙ MSP, for every rotation of a pulsar over long time periods—can pre- J1614−2230 (ref. 4) (though the originally reported mass was cisely measure a wide variety of physical phenomena, includ- 1.97 ± 0.04 M⊙, continued timing has led to a more precise mass 5 ing those that allow the measurement of the masses of the measurement of 1.928 ± 0.017 M⊙ by Fonseca et al.
    [Show full text]
  • Observational Evidence for Stellar Mass Black Holes
    J. Astrophys. Astr. (1999) 20, 197–210 Observational Evidence for Stellar Mass Black Holes Tariq Shahbaz, University of Oxford, Department of Astrophysics, Nuclear Physics Building, Keble Road, Oxford, 0X1 3RH, England. e-mail:[email protected] Abstract. I review the evidence for stellar mass black holes in the Galaxy. The unique properties of the soft X-ray transient (SXTs) have provided the first opportunity for detailed studies of the mass-losing star in low-mass X-ray binaries. The large mass functions of these systems imply that the compact object has a mass greater than the maximum mass of a neutron star, strengthening the case that they contain black holes. The results and techniques used are discussed. I also review the recent study of a comparison of the luminosities of black hole and neutron star systems which has yielded compelling evidence for the existence of event horizons. Key words. X-ray sources—black holes. 1. Black holes and the soft X-ray transients It is widely believed that black holes power AGN and some X-ray binaries, and that they inhabit the nuclei of many normal galaxies. The compulsion to believe that black holes are physical objects is driven by our faith in general relativity and the idea that a black hole is a logical end point of stellar and galactic evolution. The proof for the existence of stellar black holes has been a subject of considerable effort for the last three decades, since the first dynamical mass estimate for the compact object in Cyg X-l (Webster & Murdin 1972; Bolton 1972).
    [Show full text]
  • Millisecond Pulsars, Their Evolution and Applications
    J. Astrophys. Astr. (September 2017) 38:42 © Indian Academy of Sciences DOI 10.1007/s12036-017-9469-2 Review Millisecond Pulsars, their Evolution and Applications R. N. MANCHESTER CSIRO Astronomy and Space Science, P.O. Box 76, Epping, NSW 1710, Australia. E-mail: [email protected] MS received 15 May 2017; accepted 28 July 2017; published online 7 September 2017 Abstract. Millisecond pulsars (MSPs) are short-period pulsars that are distinguished from “normal” pulsars, not only by their short period, but also by their very small spin-down rates and high probability of being in a binary system. These properties are consistent with MSPs having a different evolutionary history to normal pulsars, viz., neutron-star formation in an evolving binary system and spin-up due to accretion from the binary companion. Their very stable periods make MSPs nearly ideal probes of a wide variety of astrophysical phenomena. For example, they have been used to detect planets around pulsars, to test the accuracy of gravitational theories, to set limits on the low-frequency gravitational-wave background in the Universe, and to establish pulsar-based timescales that rival the best atomic-clock timescales in long-term stability. MSPs also provide a window into stellar and binary evolution, often suggesting exotic pathways to the observed systems. The X-ray accretion- powered MSPs, and especially those that transition between an accreting X-ray MSP and a non-accreting radio MSP, give important insight into the physics of accretion on to highly magnetized neutron stars. Keywords. Pulsars—general—stars: evolution—gravitation. 1. Introduction pulsar was found in September 1982 at Arecibo Obser- vatory in a very high time-resolution search of the The first pulsars discovered (Hewish et al.
    [Show full text]
  • The Mass-Ratio Distribution of Spectroscopic Binaries Henri M.J
    The mass-ratio distribution of spectroscopic binaries Henri M.J. Boffin ESO, Vitacura, Santiago, Chile. [email protected] Introduction The distribution of orbital elements, and in particular the orbital period and the eccentricity, can reveal much about the formation mechanisms of binary systems as well as their subsequent evolution. In the same vein, the distributions of the masses of the two components, M1 and M2, or similarly, of M1 and the mass ratio, q=M2/M1, are clues to critical questions related to binaries: did the binaries form through random pairing (in which case the mass of the individual components would be drawn from the IMF)? Does the mass ratio distribution depend on the primary mass (as does apparently the multiplicity of stars)? How will the systems evolve (some systems being possible only if the mass ratio is close to one, i.e. the system is made of quasi-twins)? How do families of stars compare to each other? It is thus a reasonable thing to do to try to estimate for different samples of binary stars the distribution of their mass ratios and many attempts have been done in the literature. I will hereby review some of the pitfalls of such endeavours. 1. Spectroscopic binaries and exoplanets We can distinguish between single- and double-lined spectroscopic binary (SB1 and SB2), depending on whether we can see the radial velocity variations of one or both components. The distinction will be due to the magnitude difference between the components, as too large a difference impedes the detection of the secondary star.
    [Show full text]