DOCSLIB.ORG

Modeling and Digital Control of High Frequency Dc-Dc Power Converters

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Modeling and Digital Control of High Frequency Dc-Dc Power Converters University of Central Florida STARS Electronic Theses and Dissertations, 2004-2019 2007 Modeling And Digital Control Of High Frequency Dc-dc Power Converters Yangyang Wen University of Central Florida Part of the Electrical and Electronics Commons Find similar works at: https://stars.library.ucf.edu/etd University of Central Florida Libraries http://library.ucf.edu This Doctoral Dissertation (Open Access) is brought to you for free and open access by STARS. It has been accepted for inclusion in Electronic Theses and Dissertations, 2004-2019 by an authorized administrator of STARS. For more information, please contact [email protected]. STARS Citation Wen, Yangyang, "Modeling And Digital Control Of High Frequency Dc-dc Power Converters" (2007). Electronic Theses and Dissertations, 2004-2019. 3407. https://stars.library.ucf.edu/etd/3407 MODELING AND DIGITAL CONTROL OF HIGH FREQUENCY DC-DC POWER CONVERTERS by YANGYANG WEN B.E., Chongqing University, P. R. China, 1996 M.S., Chongqing University, P. R. China, 1999 M.S., University of Central Florida, USA, 2004 A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the School of Electrical Engineering and Computer Science in the College of Engineering and Computer Science at the University of Central Florida Orlando, Florida Spring Term 2007 Major Professor: Issa Batarseh © 2007 Yangyang Wen ii ABSTRACT The power requirements for leading edge digital integrated circuits have become increasingly demanding. Power converter systems must be faster, more flexible, more precisely controllable and easily monitored. Meanwhile, in addition to control process, the new functions such as power sequencing, communication with other systems, voltage dynamic programming, load line specifications, phase current balance, protection, power status monitoring and system diagnosis are going into today’s power supply systems. Digital controllers, compared with analog controllers, are in a favorable position to provide basic feedback control as well as those power management functions with lower cost and great flexibility. The dissertation gives an overview of digital controlled power supply systems by comparing with conventional analog controlled power systems in term of system architecture, modeling methods, and design approaches. In addition, digital power management, as one of the most valuable and “cheap” function, is introduced in Chapter 2. Based on a leading-edge digital controller product, Chapter 3 focuses on digital PID compensator design methodologies, design issues, and optimization and development of digital controlled single-phase point-of-load (POL) dc-dc converter. Nonlinear control is another valuable advantage of digital controllers over analog controllers. Based on the modeling of an isolated half-bridge dc-dc converter, a nonlinear control method is proposed in Chapter 4. Nonlinear adaptive PID compensation scheme is implemented based on digital controller Si8250. The variable PID coefficient during transients improves power system’s transient response and thus output capacitance can be reduced to save cost. In iii Chapter 5, another nonlinear compensation algorithm is proposed for asymmetric flyback- forward half bridge dc-dc converter to reduce the system loop gain’s dependence on the input voltage, and improve the system’s dynamic response at high input line. In Chapter 6, a unified pulse width modulation (PWM) scheme is proposed to extend the duty-cycle-shift (DCS) control, where PWM pattern is adaptively generated according to the input voltage level, such that the power converter’s voltage stress are reduced and efficiency is improved. With the great flexibility of digital PWM modulation offered by the digital controller Si8250, the proposed control scheme is implemented and verified. Conclusion of the dissertation work and suggestions for future work in related directions are given in final Chapter. iv This document is dedicated to my parents. v ACKNOWLEDGMENTS I would like to express my sincere appreciation to my advisor, Dr. Issa Batarseh, for his for his guidance, encouragement and support. Dr. Issa Batarseh’s extensive vision and creative thinking have been the source of inspiration for me throughout this work. His personality and management experience are examples for me. I am grateful to my committee members, Dr. Louis Chow, Dr. Wasfy Mikhael, Dr. Christopher Iannello, Dr. Takis Kasparis, Dr. Jiann S. Yuan and Dr. Thomas Wu for their valuable suggestions and numerous help. It was a great pleasure to work in the Power Electronics Laboratory at the University of Central Florida Center. I am truly indebted to Dr. Hong Mao, Dr. Jaber A. Abu Qahouq, Dr. Shiguo Luo, Dr. Weihong Qiu, for their valuable guidance and help, made this dissertation possible. I would also like to acknowledge my team members Dr. Songquan Deng , Osama Abdul-Rahman, Liangbin Yao, Shangyang Xiao for their useful discussion and support. I would like to thank the digital power group in Silabs, Don Alfano, Ka leung and Jinwen Xiao. It is a pleasure to work with such a talented, hard-working and creative group. And I also like to express my gratitude to my friends, Jinwen Xiao, Yufang Jin, Alex Cai, Xiaolin Guo, their friendship and help have made my stay in Austin pleasant and enjoyable. My heartfelt appreciation goes toward my family who has always been there with their love and encouragement. Yangyang Wen March 2007 vi TABLE OF CONTENTS LIST OF FIGURES ....................................................................................................................... xi LIST OF TABLES...................................................................................................................... xvii 1 INTRODUCTION ....................................................................................................................... 1 1.1 Background and Motivations.......................................................................................... 1 1.2 Dissertation Outline and Major Results.......................................................................... 9 2 ANALOG AND DIGITAL CONTROLLED DC-DC CONVERTERS ................................... 13 2.1 Introduction................................................................................................................... 13 2.2 Modeling of High Frequency Switching DC-DC Converters....................................... 14 2.3 Analog Controlled DC-DC Converters......................................................................... 21 2.4 Digital Controlled Power Converter and Theoretical Basis ......................................... 25 2.5 Digital Controller Design Methodology ....................................................................... 31 2.6 Digital Power System Management.............................................................................. 41 2.7 Summary....................................................................................................................... 47 3 ALGORITHMS AND DESIGN OPTIMIZATION BASED ON DIGITAL CONTROLLER SI8250........................................................................................................................................... 49 3.1 Introduction................................................................................................................... 49 3.2 Digital control design for power converters ................................................................. 51 3.3 Digital Controller Design Case Study........................................................................... 58 3.4 Digital PID Coefficients Optimization and Limitation................................................. 64 3.4.1 Optimization of Digital Coefficients ........................................................................ 64 3.4.2 ADC and DPWM design considerations .................................................................. 72 vii 3.4.3 Limitation and calculation error of digital coefficients ............................................ 76 3.5 Digital controller Si8250 introduction.......................................................................... 83 3.5.1 Si8250 overview....................................................................................................... 83 3.5.2 System operation....................................................................................................... 85 3.5.3 ADC and Reference DAC......................................................................................... 87 3.5.4 Si8250 filter engine................................................................................................... 88 3.5.5 DPWM ...................................................................................................................... 90 3.5.6 System Management Processor ................................................................................ 93 3.6 Digital controller design implementation – Single-phase POL converter.................... 94 3.6.1 Hardware and specification overview....................................................................... 94 3.6.2 Control loop design................................................................................................... 97 3.6.3 Non-linear transient response control ..................................................................... 103 3.6.4 Experiment results.................................................................................................. 104 3.7 Summary....................................................................................................................
Load more

Recommended publications
  • Digital Proportional Amplifier of Linear DC Electromagnet
    International Journal of Scientific & Engineering Research Volume 10, Issue 10, October-2019 257 ISSN 2229-5518 Digital proportional amplifier of linear DC electromagnet 1’Hazrat Ali ([email protected]) 2’Wang Xuping ([email protected]) 3’Muhammad Hasham Khan ([email protected]) 4’Haseeb Yar Hiraj ([email protected]) 5’Muhammad Zeeshan Adil([email protected]) Abstract— Digital Signal Processor (DSP) based embedded code generation which is obtained automatically in PSIM software for Permanent Magnet Synchronous Motor (PMSM) control system. The simulation model of the PMSM control system is developed in PSIM environment using Motor Control Blocks and Embedded Target for TI 2000805 block. This control block diagram is send to Sim Coder to generate C-code that is ready to run on the DSP hardware, Sim Coder also creates the complete project files for the TI Code Composer Studio development environment where the code will be compiled, linked, and uploaded to the DSP using High Voltage Motor Control-PFC Kit. So, embedded code generation provides a very quick way to design a motor drive system from user specifications also programming greatly simplifies the generation, prototyping and modification of DSP based design, thus decreasing the development cycle time. Index Terms— Digital Signal Processing Motor Control, PMSM, DSP, Embedded Code Generation, PSIM. —————————— —————————— I. INTRODUCTION H igh capacity and qualification in industry, the permanent magnet synchronous motor (PMSM) has greatly accepted between the various types of alternative current motors. The PMSM’s have been increasingly applied for drive applications, such as robotics and weapon servo-control systems, due to their high power density, torque to inertia ratio and high efficiency [1].
    [Show full text]
  • Chapter 3 Permanent Magnet Synchronous Motor
    Faculdade de Engenharia da Universidade do Porto Traction Control in Electric Vehicles Tiago Oliveira Bastos Pinto de Sá Dissertation prepared under the Master in Electrical and Computers Engineering Major Automation Supervisor: Adriano Carvalho July 2012 © Tiago Sá, 2012 ii To my mother and grandma iii iv Resumo O sector dos transportes é um dos maiores setores industriais hoje em dia. Desde o desenvolvimento do motor de combustão interna e da sua aplicação ao setor dos transportes, as pessoas estão cada vez mais dependentes de uma forma económica e confortável de viajar. Com o aumento do preço dos combustíveis fósseis causado pela sua procura excessiva, e com as recentes preocupações ambientais relativas à emissão de gases poluentes gerados pela queima do combustível, a existência de uma alternativa é fulcral. A forma de transporte alternativo mais comum num ambiente urbano é o autocarro. É mais barato, mais conveniente em determinados casos e produz menos poluição per capita do que um carro próprio. No entanto, continua a poluir. Com isto em mente, e com a recente eminência dos motores elétricos no setor dos transportes, é analisado o controlo de motores síncronos de ímanes permanentes, em particular a aplicação de um de 150kW num autocarro elétrico. O objetivo deste documento é analisar o domínio do controlo na mobilidade elétrica e discutir o projeto do controlador que alimenta o motor, permitindo o seu acionamento e travagem, com a possibilidade de regenerar a energia da travagem, recarregando dessa forma as baterias. O sistema deverá ser capaz de funcionar sem sensores de velocidade ou posição. Pretende-se validar os resultados obtidos na simulação aplicando um motor menos potente do que o objetivo final, de forma a poder validar laboratorialmente esses mesmos resultados.
    [Show full text]
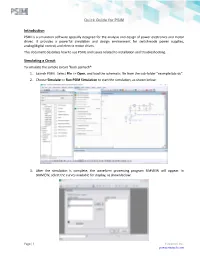
  • Quick Guide for PSIM Introduction Simulating a Circuit
    Quick Guide for PSIM Introduction PSIM is a simulation software specially designed for the analysis and design of power electronics and motor drives. It provides a powerful simulation and design environment for switchmode power supplies, analog/digital control, and electric motor drives. This document describes how to use PSIM, and issues related to installation and troubleshooting. Simulating a Circuit To simulate the sample circuit "buck.psimsch": 1. Launch PSIM. Select File >> Open, and load the schematic file from the sub-folder “examples\dc-dc”. 2. Choose Simulate >> Run PSIM Simulation to start the simulation, as shown below: 3. After the simulation is complete, the waveform processing program SIMVIEW will appear. In SIMVIEW, select the curves available for display, as shown below: Page | 1 Powersim Inc. powersimtech.com Quick Guide for PSIM Setting up Co-Simulation with Matlab/Simulink PSIM can perform co-simulation with Matlab/Simulink. When PSIM is installed, if the SimCoupler Module is enabled in the license, the installation will set up the co-simulation between PSIM and Matlab/Simulink automatically. If you change the PSIM folder name after PSIM is installed, you must run “SetSimPath.exe” in the PSIM directory to set up the co-simulation again. If you are running multiple versions of PSIM or Matlab/Simulink, to associate a specific version of PSIM with a specific version of Matlab/Simulink, from the directory of that PSIM version, run “SetSimPath.exe” located in the PSIM installation folder, and select the desired Matlab/Simulink version. To see how the co-simulation works, follow the steps below to simulate the sample circuit “chop1q_ifb_simulink_r13.mdl”: 1.
    [Show full text]
  • PSIM Presentation
    Powersys SUPERCACITOR MODEL IN PSIM Adrien MICHEL POWERSYS International Workshop on Supercapacitors and Energy Storage « SUPERCAPACITORS: On the Pulse of a Revolution » Tuesday 23rd May 2017, ENEA - Bologna, Italy Outline Presentation ✓ POWERSYS overview ✓ PSIM overview and main functions / capabilities ✓ PSIM model for Supercapacitor ✓ Application on automobile hybrid energy storage Powersys: Presentation Powersys is a French consulting and software company providing global solutions of engineering software and services in the field of Electrical & Electromechanical Power Systems. Comprehensive Software offer for Complete range of services: power system applications ▪ Support ▪ Studies Software Services ▪ Training Expert Community Strong relations with the developers to provide the best solution. Connection to a worldwide network of experts, industrial and academic partners. Powersys: A worldwide Presence POWERSYS, France POWERSYS, Canada Corporate headquarters POWERSYS, Germany POWERSYS, USA Softline POWERSYS, Ipetco Hsoft India POWERSYS, India Keliang NEAT CO Tecknocea SAM-A Solutions Elec Soft Astek Future Technologies Legend V Power Offices Powersys Voltex EMTP-RV Distributors Software developers Powersys: Software Distribution Power Systems Transients Power Electronics, Drive and Mechatronic Systems Electromechanical Design PSIM Software Dynamic Simulation Platform for Power Electronics and Motor Drives About PSIM • The Developer of PSIM is www.powersimtech.com • PSIM is born in 1994 in United States • Powersys is the exclusive distributor in Europe • Used in over 70 countries worldwide by thousand of customers PSIM Accelerates Your Pace of Innovation! What is PSIM? • PSIM is a simulation software specifically designed for power electronics, motor drives, and energy conversion applications. • Old version It is positioned between a device/circuit simulator (such as SPICE) and a system/control simulator (such as Matlab/Simulink).
    [Show full text]
  • SHIL and DHIL Simulations of Nonlinear Control Methods Applied for Power Converters Using Embedded Systems
    electronics Article SHIL and DHIL Simulations of Nonlinear Control Methods Applied for Power Converters Using Embedded Systems Arthur H. R. Rosa * , Matheus B. E. Silva, Marcos F. C. Campos, Renato A. S. Santana, Welbert A. Rodrigues, Lenin M. F. Morais and Seleme I. Seleme Jr. Graduate Program in Electrical Engineering, Universidade Federal de Minas Gerais, Av. Antônio Carlos 6627, Belo Horizonte 31270-901, MG, Brazil; [email protected] (M.B.E.S.); [email protected] (M.F.C.C.); [email protected] (R.A.S.S.); [email protected] (W.A.R.); [email protected] (L.M.F.M.); [email protected] (S.I.S.J.) * Correspondence: [email protected] Received: 17 August 2018; Accepted: 30 September 2018; Published: 6 October 2018 Abstract: In this work, a new real-time Simulation method is designed for nonlinear control techniques applied to power converters. We propose two different implementations: in the first one (Single Hardware in The Loop: SHIL), both model and control laws are inserted in the same Digital Signal Processor (DSP), and in the second approach (Double Hardware in The Loop: DHIL), the equations are loaded in different embedded systems. With this methodology, linear and nonlinear control techniques can be designed and compared in a quick and cheap real-time realization of the proposed systems, ideal for both students and engineers who are interested in learning and validating converters performance. The methodology can be applied to buck, boost, buck-boost, flyback, SEPIC and 3-phase AC-DC boost converters showing that the new and high performance embedded systems can evaluate distinct nonlinear controllers.
    [Show full text]
  • User's Guide ®
    ® PSIM User’s Guide Powersim Inc. Chapter : -7 PSIM® User’s Guide Version 9.0 Release 2 March 2010 Copyright © 2001-2010 Powersim Inc. All rights reserved. No part of this manual may be photocopied or reproduced in any form or by any means without the written permission of Powersim Inc. Disclaimer Powersim Inc. (“Powersim”) makes no representation or warranty with respect to the adequacy or accuracy of this documentation or the software which it describes. In no event will Powersim or its direct or indirect suppliers be liable for any damages whatsoever including, but not limited to, direct, indirect, incidental, or consequential damages of any character including, without limitation, loss of business profits, data, business information, or any and all other commercial damages or losses, or for any damages in excess of the list price for the licence to the software and documentation. Powersim Inc. email: [email protected] http://www.powersimtech.com -6 Chapter : Contents 1 General Information 1.1 Introduction 1 1.2 Circuit Structure 2 1.3 Software/Hardware Requirement 3 1.4 Installing the Program 3 1.5 Simulating a Circuit 3 1.6 Component Parameter Specification and Format 3 2 Power Circuit Components 2.1 Resistor-Inductor-Capacitor Branches 7 2.1.1 Resistors, Inductors, and Capacitors 7 2.1.2 Rheostat 8 2.1.3 Saturable Inductor 8 2.1.4 Nonlinear Elements 9 2.2 Switches 10 2.2.1 Diode, LED, Zener Diode, and DIAC 10 2.2.2 Thyristor and TRIAC 12 2.2.3 GTO and Transistors 13 2.2.4 Bi-Directional Switches 15 2.2.5 Linear Switches 16 2.2.6
    [Show full text]
  • Darvill 2018.Pdf
    ANGLIA RUSKIN UNIVERSITY FACULTY OF SCIENCE AND TECHNOLOGY CONCEPTUAL DEVELOPMENT OF A NOVEL DIGITAL CONTROLLER FOR OPTIMISED OPERATION OF A HYBRID RENEWABLE ENERGY SYSTEM JOHN DARVILL A thesis in partial fulfilment of the requirements of Anglia Ruskin University for the degree of Doctor of Philosophy Submitted January 2018 Acknowledgements I would like to express my deep gratitude to my supervisor, Dr Alin Tisan, for his consistent support and guidance over the last five years. I would also like to offer my thanks to my second supervisor, Professor Marcian Cirstea, not only for his support during my PhD but also for inspiring me during my undergraduate degree and sparking my interest in this topic. This project would not have been possible without the invaluable input you both offered. i ANGLIA RUSKIN UNIVERSITY ABSTRACT FACULTY OF SCIENCE AND TECHNOLOGY CONCEPTUAL DEVELOPMENT OF A NOVEL DIGITAL CONTROLLER FOR OPTIMISED OPERATION OF A HYBRID RENEWABLE ENERGY SYSTEM JOHN DARVILL January 2018 The popularity of renewable energy has increased dramatically in the last decade as it becomes increasingly apparent that an alternative to fossil fuel is required. In order for this market to continue to grow, there are a number of technical issues which must be overcome. One such issue is the instability of power supplies which rely on unpredictable natural resources. A popular solution to this problem is the use of a number of complementary renewable power sources to create a stable power network serving a small geographical area. In this project, a novel control solution for such a system is proposed and modelled using a new approach.
    [Show full text]
  • SPICE Module User’S Guide
    SPICE Module User’s Guide Powersim Inc. Chapter : -3 SPICE Module User’s Guide Version 12.0 Release 1 July 2019 Copyright © 2016-2019 Powersim Inc. All rights reserved. No part of this manual may be photocopied or reproduced in any form or by any means without the written permission of Powersim Inc. Disclaimer Powersim Inc. (“Powersim”) makes no representation or warranty with respect to the adequacy or accuracy of this documentation or the software which it describes. In no event will Powersim or its direct or indirect suppliers be liable for any damages whatsoever including, but not limited to, direct, indirect, incidental, or consequential damages of any character including, without limitation, loss of business profits, data, business information, or any and all other commercial damages or losses, or for any damages in excess of the list price for the licence to the software and documentation. Powersim Inc. Email: [email protected] powersimtech.com -2 Chapter : Contents 1 Introduction 2 PSIM-SPICE Interface 2.1 Overview 3 2.2 SPICE Model Libraries 3 2.2.1 SPICElib Folder 3 2.2.2 Search Paths for SPICE Models 3 2.2.3 Directives .LIB and .INCLUDE 4 2.2.4 Set Path for LTspice Executable 4 2.2.5 Find SPICE Models in Libraries 4 2.2.6 Netlist Syntax Check 5 2.3 Simulation Control Dialog Options for SPICE Simulation 6 2.3.1 Transient Analysis 6 2.3.2 AC Analysis 7 2.3.3 DC Analysis 8 2.3.4 Step Run Option 9 2.3.5 Other Analysis Options 9 2.4 PSIM Elements for SPICE Simulation 10 2.4.1 Multi-Level Elements 10 2.4.2 SPICE Directive
    [Show full text]
  • Power Electronics: Computer Simulation and Analysis
    PROJECT REPORT ON PPOOWWEERR EELLEECCTTRROONNIICCSS:: CCOOMMPPUUTTEERR SSIIMMUULLAATTIIOONN AANNDD AANNAALLYYSSIISS By: Ravi Shankar Singh (10502024) Byaktiranjan Pattanayak (10502030) Shankar Kumar (10502036) B.Tech 8TH SEMESTER Electrical Engineering. Under the guidance of PROF. P.C.PANDA ELECTRICAL ENGINEERING DEPARTMENT NIT ROURKELA ELECTRICAL ENGINEERING DEPARTMENT NATIONAL INSTITUTE OF TECHNOLOGY ROURKELA CERTIFICATE This is to certify that the thesis entitle, “POWER ELECTRONICS:COMPUTER SIMULATION AND ANALYSIS” submitted by Sh. BYAKTIRANJAN PATTANAYAK (10502030) in partial fulfilment of the requirements for the award of Bachelor of Technology Degree in Electrical Engineering at the National Institute of Technology, Rourkela (Deemed University) is an authentic work carried out by him under my supervision and guidance. PLACE: ROURKELA (P.C.PANDA) DATE: PROFESSOR ELECTRICAL ENGINEERING DEPARTMENT NATIONAL INSTITUTE OF TECHNOLOGY ROURKELA CERTIFICATE This is to certify that the thesis entitle, “POWER ELECTRONICS:COMPUTER SIMULATION AND ANALYSIS” submitted by Sh. RAVISHANKAR SINGH (10502024) in partial fulfilment of the requirements for the award of Bachelor of Technology Degree in Electrical Engineering at the National Institute of Technology, Rourkela (Deemed University) is an authentic work carried out by him under my supervision and guidance. PLACE: ROURKELA (P.C.PANDA) DATE: PROFESSOR ELECTRICAL ENGINEERING DEPARTMENT NATIONAL INSTITUTE OF TECHNOLOGY ROURKELA CERTIFICATE This is to certify that the thesis entitle, “POWER ELECTRONICS:COMPUTER SIMULATION AND ANALYSIS” submitted by Sh. SHANKAR KUMAR (10502036) in partial fulfilment of the requirements for the award of Bachelor of Technology Degree in Electrical Engineering at the National Institute of Technology, Rourkela (Deemed University) is an authentic work carried out by him under my supervision and guidance. PLACE: ROURKELA (P.C.PANDA) DATE: PROFESSOR ACKNOWLEDGEMENT: We wish to express our sincere gratitude to our project supervisor Prof.
    [Show full text]
  • PSIM User Manual.Book
    ® User’s Guide Powersim Inc. Chapter : -7 PSIM® User’s Guide Version 11.1 Release 2 November 2017 Copyright © 2001-2017 Powersim Inc. All rights reserved. No part of this manual may be photocopied or reproduced in any form or by any means without the written permission of Powersim Inc. Disclaimer Powersim Inc. (“Powersim”) makes no representation or warranty with respect to the adequacy or accuracy of this documentation or the software which it describes. In no event will Powersim or its direct or indirect suppliers be liable for any damages whatsoever including, but not limited to, direct, indirect, incidental, or consequential damages of any character including, without limitation, loss of business profits, data, business information, or any and all other commercial damages or losses, or for any damages in excess of the list price for the licence to the software and documentation. Powersim Inc. email: [email protected] http://www.powersimtech.com -6 Chapter : Contents 1 General Information 1.1 Introduction 1 1.2 Circuit Structure 3 1.3 Software/Hardware Requirement 3 1.4 Installing the Program 3 1.5 Simulating a Circuit 4 1.6 Simulation Control 4 1.7 Component Parameter Specification and Format 8 2 Circuit Schematic Design 2.1 PSIM Environment 11 2.2 Creating a Circuit 14 2.3 File Menu 15 2.4 Edit Menu 15 2.5 View Menu 17 2.6 Design Suites Menu 17 2.7 Subcircuit Menu 18 2.7.1 Creating Subcircuit - In the Main Circuit 19 2.7.2 Creating Subcircuit - Inside the Subcircuit 19 2.7.3 Connecting Subcircuit - In the Main Circuit 20 2.7.4
    [Show full text]
  • PSIM User's Guide
    PSIM User’s Guide Powersim Inc. -9 PSIM User’s Guide Version 7.0 Release 3 May 2006 Copyright © 2001-2006 Powersim Inc. All rights reserved. No part of this manual may be photocopied or reproduced in any form or by any means without the written permission of Powersim Inc. Disclaimer Powersim Inc. (“Powersim”) makes no representation or warranty with respect to the adequacy or accuracy of this documentation or the software which it describes. In no event will Powersim or its direct or indirect suppliers be liable for any damages whatsoever including, but not limited to, direct, indirect, incidental, or consequential damages of any character including, without limitation, loss of business profits, data, business information, or any and all other commercial damages or losses, or for any damages in excess of the list price for the licence to the software and documentation. Powersim Inc. email: [email protected] http://www.powersimtech.com -8 Contents 1 General Information 1.1 Introduction 1 1.2 Circuit Structure 2 1.3 Software/Hardware Requirement 3 1.4 Installing the Program 3 1.5 Simulating a Circuit 4 1.6 Component Parameter Specification and Format 4 2 Power Circuit Components 2.1 Resistor-Inductor-Capacitor Branches 7 2.1.1 Resistors, Inductors, and Capacitors 7 2.1.2 Rheostat 8 2.1.3 Saturable Inductor 9 2.1.4 Nonlinear Elements 10 2.2 Switches 11 2.2.1 Diode, DIAC, and Zener Diode 12 2.2.2 Thyristor and TRIAC 13 2.2.3 GTO, Transistors, and Bi-Directional Switch 15 2.2.4 Linear Switches 17 2.2.5 Switch Gating Block 19 2.2.6 Single-Phase
    [Show full text]
  • Design of Isolated Dc-Dc and Dc-Dc-Ac Converters with Reduced
    DESIGN OF ISOLATED DC-DC AND DC-DC-AC CONVERTERS WITH REDUCED NUMBER OF POWER SWITCHES A Thesis Submitted to the Faculty of Purdue University by Dhara I. Mallik In Partial Fulfillment of the Requirements for the Degree of Master of Science in Electrical and Computer Engineering August 2017 Purdue University Indianapolis, Indiana ii THE PURDUE UNIVERSITY GRADUATE SCHOOL STATEMENT OF COMMITTEE APPROVAL Dr. Euzeli Cipriano dos Santos, Chair Department of Electrical and Computer Engineering Dr. Mohamed El-Sharkawy Department of Electrical and Computer Engineering Dr. Maher Rizkalla Department of Electrical and Computer Engineering Approved by: Dr. Brian King Head of the Graduate Program iii Dedicated to my beloved parents Munmun Manabee and Dr. M S I Mullick Ma r Bapi iv ACKNOWLEDGMENTS I would like to thank my thesis supervisor and mentor Dr. Euzeli C. dos Santos, for his guidance and inspiration through the research process and course-works. I am grateful to all my committee members. I am immensely indebted to Dr. Brian King, the Head of the Department, not only for his guidance since the very first year of my graduate studies but also for being a continuous support. I am grateful to the other faculty members and staff. I would especially like to mention Sherrie for keep enduring my constant nudging always with a welcoming smile. I want to thank my lab-mates for their support whenever I asked and even when I did not ask. I owe everything to my loving parents who kept sacrificing for me since the day I was born. Even being a thousand of miles away, they never stopped encouraging, motivating and telling me to dream bigger.
    [Show full text]