Perpendicular Lines
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Circle Theorems
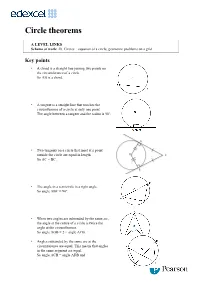
Circle theorems A LEVEL LINKS Scheme of work: 2b. Circles – equation of a circle, geometric problems on a grid Key points • A chord is a straight line joining two points on the circumference of a circle. So AB is a chord. • A tangent is a straight line that touches the circumference of a circle at only one point. The angle between a tangent and the radius is 90°. • Two tangents on a circle that meet at a point outside the circle are equal in length. So AC = BC. • The angle in a semicircle is a right angle. So angle ABC = 90°. • When two angles are subtended by the same arc, the angle at the centre of a circle is twice the angle at the circumference. So angle AOB = 2 × angle ACB. • Angles subtended by the same arc at the circumference are equal. This means that angles in the same segment are equal. So angle ACB = angle ADB and angle CAD = angle CBD. • A cyclic quadrilateral is a quadrilateral with all four vertices on the circumference of a circle. Opposite angles in a cyclic quadrilateral total 180°. So x + y = 180° and p + q = 180°. • The angle between a tangent and chord is equal to the angle in the alternate segment, this is known as the alternate segment theorem. So angle BAT = angle ACB. Examples Example 1 Work out the size of each angle marked with a letter. Give reasons for your answers. Angle a = 360° − 92° 1 The angles in a full turn total 360°. = 268° as the angles in a full turn total 360°. -

Angles ANGLE Topics • Coterminal Angles • Defintion of an Angle
Angles ANGLE Topics • Coterminal Angles • Defintion of an angle • Decimal degrees to degrees, minutes, seconds by hand using the TI-82 or TI-83 Plus • Degrees, seconds, minutes changed to decimal degree by hand using the TI-82 or TI-83 Plus • Standard position of an angle • Positive and Negative angles ___________________________________________________________________________ Definition: Angle An angle is created when a half-ray (the initial side of the angle) is drawn out of a single point (the vertex of the angle) and the ray is rotated around the point to another location (becoming the terminal side of the angle). An angle is created when a half-ray (initial side of angle) A: vertex point of angle is drawn out of a single point (vertex) AB: Initial side of angle. and the ray is rotated around the point to AC: Terminal side of angle another location (becoming the terminal side of the angle). Hence angle A is created (also called angle BAC) STANDARD POSITION An angle is in "standard position" when the vertex is at the origin and the initial side of the angle is along the positive x-axis. Recall: polynomials in algebra have a standard form (all the terms have to be listed with the term having the highest exponent first). In trigonometry, there is a standard position for angles. In this way, we are all talking about the same thing and are not trying to guess if your math solution and my math solution are the same. Not standard position. Not standard position. This IS standard position. Initial side not along Initial side along negative Initial side IS along the positive x-axis. -

Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential -

Classify Each Triangle by Its Side Lengths and Angle Measurements
GRADE 4 | MODULE 4 | TOPIC D | LESSONS 12–16 KEY CONCEPT OVERVIEW In Lessons 12 through 16, students explore lines of symmetry and characteristics of triangles and quadrilaterals. You can expect to see homework that asks your child to do the following: ▪ Find and draw lines of symmetry. ▪ Given half of a figure and the line of symmetry, draw the other half of the figure. ▪ Classify triangles by side lengths (e.g., equilateral, isosceles, scalene) and by angle measurements (e.g., acute, right, obtuse). ▪ Draw triangles that fit different classifications (e.g., acute and scalene). ▪ Name quadrilaterals, identify attributes (i.e., characteristics) that define them, and construct them based on given attributes. SAMPLE PROBLEM (From Lesson 13) Classify each triangle by its side lengths and angle measurements. Circle the correct names. Additional sample problems with detailed answer steps are found in the Eureka Math Homework Helpers books. Learn more at GreatMinds.org. For more resources, visit » Eureka.support GRADE 4 | MODULE 4 | TOPIC D | LESSONS 12–16 HOW YOU CAN HELP AT HOME ▪ Ask your child to look around the house for objects that have lines of symmetry. Examples include the headboard of a bed, dressers, chairs, couches, and place mats. Ask him to show where the line of symmetry would be and what makes it a line of symmetry. Be careful of objects such as doors and windows. They could have a line of symmetry, but if there’s a knob or crank on just one side, then they are not symmetrical. ▪ Ask your child to name and draw all the quadrilaterals she can think of (e.g., square, rectangle, parallelogram, trapezoid, and rhombus). -
Measuring Angles and Angular Resolution
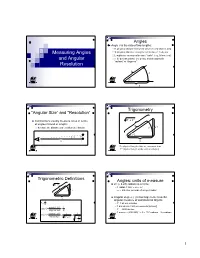
Angles Angle θ is the ratio of two lengths: R: physical distance between observer and objects [km] Measuring Angles S: physical distance along the arc between 2 objects Lengths are measured in same “units” (e.g., kilometers) and Angular θ is “dimensionless” (no units), and measured in “radians” or “degrees” Resolution R S θ R Trigonometry “Angular Size” and “Resolution” 22 Astronomers usually measure sizes in terms R +Y of angles instead of lengths R because the distances are seldom well known S Y θ θ S R R S = physical length of the arc, measured in m Y = physical length of the vertical side [m] Trigonometric Definitions Angles: units of measure R22+Y 2π (≈ 6.28) radians in a circle R 1 radian = 360˚ ÷ 2π≈57 ˚ S Y ⇒≈206,265 seconds of arc per radian θ Angular degree (˚) is too large to be a useful R S angular measure of astronomical objects θ ≡ R 1º = 60 arc minutes opposite side Y 1 arc minute = 60 arc seconds [arcsec] tan[]θ ≡= adjacent side R 1º = 3600 arcsec -1 -6 opposite sideY 1 1 arcsec ≈ (206,265) ≈ 5 × 10 radians = 5 µradians sin[]θ ≡== hypotenuse RY22+ R 2 1+ Y 2 1 Number of Degrees per Radian Trigonometry in Astronomy Y 2π radians per circle θ S R 360° Usually R >> S (particularly in astronomy), so Y ≈ S 1 radian = ≈ 57.296° 2π SY Y 1 θ ≡≈≈ ≈ ≈ 57° 17'45" RR RY22+ R 2 1+ Y 2 θ ≈≈tan[θθ] sin[ ] Relationship of Trigonometric sin[θ ] ≈ tan[θ ] ≈ θ for θ ≈ 0 Functions for Small Angles 1 sin(πx) Check it! tan(πx) 0.5 18˚ = 18˚ × (2π radians per circle) ÷ (360˚ per πx circle) = 0.1π radians ≈ 0.314 radians 0 Calculated Results -
Angles of Lines and Triangles
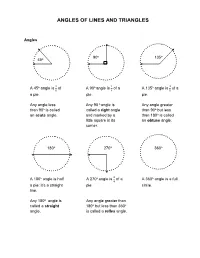
ANGLES OF LINES AND TRIANGLES Angles 90o 135o 45o o 1 o 1 o 3 A 45 angle is of A 90 angle is of a A 135 angle is of a 8 4 8 a pie. pie. pie. Any angle less Any 90 o angle is Any angle greater than 90o is called called a right angle than 90o but less an acute angle. and marked by a than 180o is called little square in its an obtuse angle. corner. 180o 270o 360o o o 3 o A 180 angle is half A 270 angle is of a A 360 angle is a full 4 a pie: it’s a straight pie. circle. line. Any 180o angle is Any angle greater than called a straight 180o but less than 360o angle. is called a reflex angle. Lines 1. Two lines are parallel ( II ) when they run next to each other but never touch. 2. Two lines are perpendicular ( _ ) when they cross at a right angle. 3. Two intersecting lines always form four angles. The sum of these angles is 360o. ao + xo + bo + yo = 360o x a b y 4. The opposite angles created by intersecting lines are always equal: a=b, x=y. 2ao + 2xo = 360o 5. Two perpendicular intersecting lines always form four 900 (“right”) angles. a x y b 6. If the sum of any two angles equals 180o, those angles are supplementary. If you know either one of them, you can find the other by subtracting the first from 180o. a x 130 x a + x = 180 130 + x = 180 180-130 = 50 x = 50o 7. -

Angle, Symmetry and Transformation 1 | Numeracy and Mathematics Glossary
Angle, symmetry and transformation T e rms Illustrations Definition Acute angle An angle greater than 0° and less than 90°. Alternate angles Where two straight lines are cut by a third, as in the diagrams, the angles d and e (also c and f) are alternate. Where the two straight lines are parallel, alternate angles are equal. 1 | Numeracy and mathematics glossary Angle, symmetry and transformation Angle An angle measures the amount of ‘turning’ between two straight lines that meet at a vertex (point). Angles are classified by their size e.g. can be obtuse, acute, right angle etc. They are measured in degrees (°) using a protractor. Axis A fixed, reference line from which locations, distances or angles are taken. Usually grids have an x axis and y axis. Bearings A bearing is used to represent the direction of one point relative to another point. It is the number of degrees in the angle measured in a clockwise direction from the north line. In this example, the bearing of NBA is 205°. Bearings are commonly used in ship navigation. 2 | Numeracy and mathematics glossary Angle, symmetry and transformation Circumference The distance around a circle (or other curved shape). Compass (in An instrument containing a magnetised pointer which shows directions) the direction of magnetic north and bearings from it. Used to help with finding location and directions. Compass points Used to help with finding location and directions. North, South, East, West, (N, S, E, W), North East (NE), South West (SW), North West (NW), South East (SE) as well as: • NNE (north-north-east), • ENE (east-north-east), • ESE (east-south-east), • SSE (south-south-east), • SSW (south-south-west), • WSW (west-south-west), • WNW (west-north-west), • NNW (north-north-west) 3 | Numeracy and mathematics glossary Angle, symmetry and transformation Complementary Two angles which add together to 90°. -

Euclidean Geometry
Euclidean Geometry Rich Cochrane Andrew McGettigan Fine Art Maths Centre Central Saint Martins http://maths.myblog.arts.ac.uk/ Reviewer: Prof Jeremy Gray, Open University October 2015 www.mathcentre.co.uk This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. 2 Contents Introduction 5 What's in this Booklet? 5 To the Student 6 To the Teacher 7 Toolkit 7 On Geogebra 8 Acknowledgements 10 Background Material 11 The Importance of Method 12 First Session: Tools, Methods, Attitudes & Goals 15 What is a Construction? 15 A Note on Lines 16 Copy a Line segment & Draw a Circle 17 Equilateral Triangle 23 Perpendicular Bisector 24 Angle Bisector 25 Angle Made by Lines 26 The Regular Hexagon 27 © Rich Cochrane & Andrew McGettigan Reviewer: Jeremy Gray www.mathcentre.co.uk Central Saint Martins, UAL Open University 3 Second Session: Parallel and Perpendicular 30 Addition & Subtraction of Lengths 30 Addition & Subtraction of Angles 33 Perpendicular Lines 35 Parallel Lines 39 Parallel Lines & Angles 42 Constructing Parallel Lines 44 Squares & Other Parallelograms 44 Division of a Line Segment into Several Parts 50 Thales' Theorem 52 Third Session: Making Sense of Area 53 Congruence, Measurement & Area 53 Zero, One & Two Dimensions 54 Congruent Triangles 54 Triangles & Parallelograms 56 Quadrature 58 Pythagoras' Theorem 58 A Quadrature Construction 64 Summing the Areas of Squares 67 Fourth Session: Tilings 69 The Idea of a Tiling 69 Euclidean & Related Tilings 69 Islamic Tilings 73 Further Tilings -

A New Method of Trisection Archimedes' Method
A New Method of Trisection David Alan Brooks David Alan Brooks was born in South Africa, where he qualified as an Air Force pilot before gaining a BA degree in classics and law, followed by an honors degree with a dissertation on ancient technology. To his regret, despite credits in sundry subjects, he has none in mathematics. After completing a second post- graduate honors degree in business administration and personnel management, he served as the deputy director of a training centre before becoming a full-time inventor. He has been granted numerous international patents. After having lived for six years on a boat, he now lives in an old chapel on a Welsh island. Thanks largely to a share of the royalties earned from two automatic poolcleaners manufactured in California, he is able to spend his days dreaming up additional geometry-intensive configurations of his revolutionary concept for efficient ultra-high-speed rotary “PHASE” engines, writing definitions for the all-limerick web dictionary OEDILF, and feeding ducks on a sacred lake once revered by Druids—also keen geometers (and perhaps frustrated trisectors) until they were crushed by the Romans in 60 AD. He won wings as a proud Air Force flyer, And strove, by degrees, to climb higher. Reduced to a tent, Then a boat (to invent), He concluded that chapels are drier. I do not, Archimedes, know why You put marks on your ruler. Sir, I Know that trisection tricks Give a trisector kicks, But why fudge when it’s easy as pi? One of the most interesting episodes in the long saga of angle trisection (see Dudley [1]) was a discovery made by Archimedes of Syracuse nearly 2300 years ago. -

Euclidean Geometry
EuclideanGeometry Thc subjectrnatrer of thrs boot rs non-Eucldcr onem-usl know wna, Euc,idean Beonre,r), . 1i,,.;liJlil.lJ,llil;li::;i::,T::.: mofe.dimculrtask th.in it ,nirhr lpp.af rniria,)"i].;llil'Jll r,, r:,",.;, ."1 .*r,'",r,,"i"t";: ;;,;;;":;;;:,., producethe vaflou! cunEnlr] ," accepreddesc prions.sirtch areari basedon rhcrerarnerr ofDavid Hitberr recenrwort o86: 1e.'.r).Nee,ess ro s;). fu*. g_.,.",r,,,. ;;; ;;;,;;;:;;;1";'i::,,"", to bedeficient and op r for yer orherchar.acter.rzatrons jde.ar ,e.,r l| new oI rhesccons ions,the rcaders ura\ no,be \umri .ed , , nd,,r,.Ju,r.. n., .hJ,en,,,e\.,r_ . ::l',.."".,' ".,..,";'',_.:; rroridi,rg^l^ rheor s'i,h:r shofthisror).orrhesubjec, ,".,",0"ou",.i.ii;:i',",Jft ili:.ll''''t, -o - Ill Anlntroduction to EuclideanGeomerrv Geomctrfin rhesense ol mensurrrionof ti!ui de\eroped bI malr)cuhurer and datesback to mrr"""i,'"i ii"',i;",ii " T ip"lll"**'rl *,"''r,,"*l ;:;;;; ;i""iil:;:;"11.:;:nil j;J,i,iJT, Ii,i.J,li.: :i:I,l.rreason,was-creared by rheG.eeks. Hrsrrlrrlrns ::ii"Jll: asr.erhar rh€ orisn of gcomerr)."" t". ,.,"J i".* ,,, tlrehres of Thatesol Milerus Ncirher or.r,i. r*.;;;-;::;#;T,:i:::il'ii:i,lirhe.\ i':filiijlli:'J:Jjli,J,il: eclips€-*npr,,r,,""u,,of 585Bc. jr is believcdthar hc ln.eddunnr rhc;jrrh cenru,-;it ;,i,,ili;."il;, probablyt'om forrotrel in m.uv orher ".." 'Lrd counrries.rnttcenrurres 1, r, fr ,,,,rr. ,t,"i r," ,- ro a:uti.e |harborh ioundhis conr : burior\ useluta|d cared . p,",o.]. ,r,.",-i,,"". ,n" lutureby ilcorTrorarngthem ".,g1 rnroi(s cd!carionorsj.sren s;me rrrccreete orihi o"r *r-,'..^-e boththe denrocraLjctbrm of governmenr and$e idcaof r trratht r,I .r p."., ,, to..e\e.) ciLizenrhar he " slr(jutdbe abte ro argn.borl cogurr4 ura perurLsiverr.or,;"" "",;,,p*"r,. -

Optimization of an Archimedean Screw
Optimization of an Archimedean Screw Alison Shappy Pat Knapp Julie Mullowney Colin Delaney Saint Michael’s College 1 Optimization of an Archimedean Screw 4/4/2013 Basic Function: How it Works Used to transport water and other materials up the length of the screw by rotating the screw on an inclined plane. http://youtu.be/5gq3Vm4vifU 2 Optimization of an Archimedean Screw 4/4/2013 History Invented around first century BC by Archimedes First detailed description of the screw was found written by Vitruvius (85BC – 20BC) Crankshafts were added to th screws in 16 century by Konrad Kyeser Rorres FIG. 2 3 Optimization of an Archimedean Screw 4/4/2013 Terms Pitch (Λ)– length of the screw from peak to peak for one cycle. K = tanθ , which gives the screw incline Chute – Area between adjacent blades, and inner and outer radii Bucket – one of the areas occupies by the trapped water within any one chute. Rorres 4 Optimization of an Archimedean Screw 4/4/2013 Terms (continued) 2 v = VT / πRo Λ , the volume ratio p = Ri / Ro , the radius ratio λ = KΛ / 2 πRo , 0 ≤ Λ ≤ 2πRo / K , the pitch ratio Rorres 5 Optimization of an Archimedean Screw 4/4/2013 Our design Goal: Maximize the amount of water carried for each turn of the screw. External Parameters: Internal Parameters: Ro = radius of screw’s outer Ri = radius of screw’s inner cylinder cylinder L = total length of screw Λ = pitch (or period) of K = slope of screw one blade (dimensionless) N = number of blades Our Parameters: Number of Blades: 2 Screw Length : 5” Outer cylinder radius: -

Angular Position
ANGULAR POSITION • To describe rotational motion, we define angular quantities that are analogous to linear quantities • Consider a bicycle wheel that is free to rotate about its axle • The axle is the axis of rotation for the wheel • If there is a small spot of red paint on the tire, we can use this reference to describe its rotational motion • The angular position of the spot is the angle θ, that a line from the axle to the spot makes with a reference line • SI unit is the radian (rad) • θ > 0 – anticlockwise rotation: θ < 0 – clockwise rotation • A radian is the angle for which the arc length, s, on a circle of radius r is equal to the radius of the circle • The arc length s for an arbitrary angle θ measured in radians is s = r θ • 1 revolution is 360°= 2 π rad • 1 rad = 360°/2 π = 57.3° 4. Rotational Kinematics 1 and Dynamics ANGULAR VELOCITY • As the bicycle wheel rotates, the angular position of the spot changes ∆ • Angular displacement is θ = θf – θi ∆ ∆t • Average angular velocity is ωav = θ/ (rad/s) v ∆x ∆t • Analogous average linear velocity av = / • Instantaneous angular velocity is the limit of ωav as the time interval ∆t reaches zero • ω > 0 – anticlockwise rotation: ω < 0 clockwise rotation • The time to complete one revolution is known as the period , T • T = 2 π/ω seconds 4. Rotational Kinematics 2 and Dynamics ANGULAR ACCELERATION • If the angular velocity of the rotating bicycle wheel increases or decreases with time, the wheel experiences an angular acceleration , α • The average angular acceleration is the change in angular velocity in a given time interval ∆ ∆t 2 • αav = ω/ rad/s • The instantaneous angular acceleration is the limit of ∆t αav as the time interval approaches zero • The sign of angular acceleration is determined by whether the change in angular velocity is positive or negative • If ω is becoming more positive (ωf > ωi), α is positive • If ω is becoming more negative (ωf < ωi), α is negative • If ω and α have the same sign, speed of rotation increasing • If ω and α have opposite signs, speed of rotation decreasing 4.