Groundwater Storage Dynamics in the World's
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Hydrochemical Zoning and Chemical Evolution of the Deep Upper Jurassic Thermal Groundwater Reservoir Using Water Chemical and Environmental Isotope Data
water Article Hydrochemical Zoning and Chemical Evolution of the Deep Upper Jurassic Thermal Groundwater Reservoir Using Water Chemical and Environmental Isotope Data Florian Heine * , Kai Zosseder and Florian Einsiedl * Chair of Hydrogeology, Department of Civil, Geo and Environmental Engineering, Technical University of Munich, Arcisstr. 21, 80333 Munich, Germany; [email protected] * Correspondence: fl[email protected] (F.H.); [email protected] (F.E.); Tel.: +49-(89)-289-25833 (F.E.) Abstract: A comprehensive hydrogeological understanding of the deep Upper Jurassic carbonate aquifer, which represents an important geothermal reservoir in the South German Molasse Basin (SGMB), is crucial for improved and sustainable groundwater resource management. Water chemical data and environmental isotope analyses of δD, δ18O and 87Sr/86Sr were obtained from groundwater of 24 deep Upper Jurassic geothermal wells and coupled with a few analyses of noble gases (3He/4He, 40Ar/36Ar) and noble gas infiltration temperatures. Hierarchical cluster analysis revealed three major water types and allowed a hydrochemical zoning of the SGMB, while exploratory factor analyses identified the hydrogeological processes affecting the water chemical composition of the thermal water. Water types 1 and 2 are of Na-[Ca]-HCO3-Cl type, lowly mineralised and have been recharged 87 86 under meteoric cold climate conditions. Both water types show Sr/ Sr signatures, stable water isotopes values and calculated apparent mean residence times, which suggest minor water-rock Citation: Heine, F.; Zosseder, K.; interaction within a hydraulically active flow system of the Northeastern and Southeastern Central Einsiedl, F. Hydrochemical Zoning Molasse Basin. This thermal groundwater have been most likely subglacially recharged in the south and Chemical Evolution of the Deep of the SGMB in close proximity to the Bavarian Alps with a delineated northwards flow direction. -

Heritage of the Birdsville and Strzelecki Tracks
Department for Environment and Heritage Heritage of the Birdsville and Strzelecki Tracks Part of the Far North & Far West Region (Region 13) Historical Research Pty Ltd Adelaide in association with Austral Archaeology Pty Ltd Lyn Leader-Elliott Iris Iwanicki December 2002 Frontispiece Woolshed, Cordillo Downs Station (SHP:009) The Birdsville & Strzelecki Tracks Heritage Survey was financed by the South Australian Government (through the State Heritage Fund) and the Commonwealth of Australia (through the Australian Heritage Commission). It was carried out by heritage consultants Historical Research Pty Ltd, in association with Austral Archaeology Pty Ltd, Lyn Leader-Elliott and Iris Iwanicki between April 2001 and December 2002. The views expressed in this publication are not necessarily those of the South Australian Government or the Commonwealth of Australia and they do not accept responsibility for any advice or information in relation to this material. All recommendations are the opinions of the heritage consultants Historical Research Pty Ltd (or their subconsultants) and may not necessarily be acted upon by the State Heritage Authority or the Australian Heritage Commission. Information presented in this document may be copied for non-commercial purposes including for personal or educational uses. Reproduction for purposes other than those given above requires written permission from the South Australian Government or the Commonwealth of Australia. Requests and enquiries should be addressed to either the Manager, Heritage Branch, Department for Environment and Heritage, GPO Box 1047, Adelaide, SA, 5001, or email [email protected], or the Manager, Copyright Services, Info Access, GPO Box 1920, Canberra, ACT, 2601, or email [email protected]. -

Groundwater Storage Dynamics in the World's
Interactive comment on “Groundwater storage dynamics in the world’s large aquifer systems from GRACE: uncertainty and role of extreme precipitation” by Mohammad Shamsudduha and Richard G. Taylor Marc Bierkens (Referee #1) [email protected] Received and published: 2 January 2020 Reviewer’s comments are italicised, and our responses (R) and revisions (REVISION) are provided in normal fonts. General comments The authors use the results of three different GRACE-based TWS methods and 4 Land surface models to generate an ensemble of groundwater storage anomalies. These are subsequently analyzed by a non-parametric statistical method to separate seasonal signals from non-linear trends and residuals. The main message of the paper is that trends in GWS anomalies (ΔGWS), if existing, are non-linear in the vast majority of main aquifer systems and that rainfall anomalies play an important role in explaining these non-linear trends. I enjoyed reading the paper. I find that it is a well-written with an important message that deserves publication. However, I have a few comments. Moderate comments: 1. I find the lack of reference to estimates based on global hydrological models (GHMS) remarkable. The first spatially distributed global assessment of depletion rates where based on such models and, albeit indirect, should be used in the discussion. They are the basis for the “narratives on global groundwater depletion” that are mentioned in the discussion and the abstract (See https://iopscience.iop.org/article/10.1088/1748- 9326/ab1a5f/meta for an overview of these studies). This is the more remarkable, given that the authors do use Land Surface Models (LSMs) to estimate ΔGWS from GRACE ΔTWS. -

Hydrogeochemical and Isotopic Indicators of Vulnerability and Sustainability in the GAS Aquifer, São Paulo State, Brazil T
Journal of Hydrology: Regional Studies 14 (2017) 130–149 Contents lists available at ScienceDirect Journal of Hydrology: Regional Studies journal homepage: www.elsevier.com/locate/ejrh Hydrogeochemical and isotopic indicators of vulnerability and sustainability in the GAS aquifer, São Paulo State, Brazil T ⁎ Trevor Elliota, , Daniel Marcos Bonottob a School of Natural and Built Environment (SNBE), Queeńs University Belfast, Stranmillis Road, Belfast, BT9 5AG, Northern Ireland, UK b Instituto de Geociências e Ciências Exatas-IGCE, Universidade Estadual Paulista-UNESP, Av. 24-A No. 1515, P.O. Box 178, CEP 13506-900, Rio Claro, São Paulo, Brazil ARTICLE INFO ABSTRACT Keywords: Study region: The Guarani Aquifer System (GAS), São Paulo State, Brazil, an important freshwater Environmental Tracers (REEs, Br/Cl, B, δ11B, resource regionally and part of a giant, transboundary system. 87 86 Sr, Sr/ Sr) Study focus: Groundwaters have been sampled along a transect. Based on environmental tracers Groundwater (REEs, Br, B, δ11B, Sr, 87Sr/86Sr) aquifer vulnerability and sustainability issues are identified. Guarani Aquifer System (GAS) New hydrological insights for the region: For sites near to aquifer outcrop, REE and Sr signatures São Paulo State (and relatively light δ13C) trace possible vertical recharge from flood basalts directly overlying Aquifer vulnerability fi Aquifer sustainability the GAS. This highlights aquifer vulnerability where con ned by fewer basalts and/or having cross-cutting fractures. 14C activities for these waters, however, suggest the impact of this re- charge is significantly delayed in reaching the GAS. Anthropogenic sources for boron are not currently encountered; δ11B highlights feldspar dissolution, isotopically lighter signatures in the deepest sampled GAS waters resulting from pH/hydrochemical speciation changes down- gradient. -

Guaraní Aquifer System Agreement
Guaraní Aquifer System Agreement Alberto Manganelli Regional Center for Groundwater Management CeReGAS - Uruguay Virtual Workshop on designing legal frameworks for transboundary water cooperation 28-29 July 2020 Guaraní Aquifer System The Guaraní Aquifer System is located in the central-eastern part of South America It underlies in the territories of Argentina, Brazil, Paraguay and Uruguay and it covers an area of 1,087,879 km2 The population located on the System is estimated at 90,000,000 inhabitants. The GAS has specific and complex physical, geological, chemical and hydraulic characteristics that were defined as part of the GEF International Waters project “Environmental Protection and Sustainable Development of the Guarani Aquifer System”. The project led to the formulation and adoption by the aquifer countries of a Strategic Action Program (SAP) aimed at the long-term sustainability of this huge freshwater resource. Following the adoption of the SA P, the aquifer countries negotiated and signed the “Guarani Aquifer Agreement” - the first shared-management agreement for a transboundary aquifer in Latin America The Guarani Aquifer Agreement (GAA) First of all it is important to highlight that the four countries sharing the GAS decided to negotiate an agreement in the absence of serious conflict over the natural resource The agreement has not yet entered into force as the last instrument of ratification remains to be deposited The GAA sets out a general management framework containing the general rules of international law applicable to transboundary water resources. Art. 2: "Each Party exercises sovereign territorial domain over their respective portions of the SAG ...." Art. 4: Countries must use the aquifer in an equitable and reasonable form. -
Data Source: FAO, UN and Water Resources
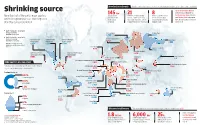
GROUNDWATER WATER DAY SPECIAL How bad is it already Aquifers under most stress are in poor and populated regions, where alternatives are limited Shrinking source Ganga-Brahmaputra Basin in 145 km3 21 8 India, Nepal and Bangladesh, More than half of the world's major aquifers, The amount of of world's 37 largest aquifer of these 21 aquifer systems North Caucasus Basin in Russia groundwater the systemsÐshaded in redÐlost are overstressed, which and Canning Basin in Australia which store groundwater, are depleting faster world extracts water faster than they could be means they get hardly any have the fastest rate of depletion than they can be replenished every year recharged between 2003 and 2013 natural recharge in the world Aquifer System where groundwater levels are depleting Pechora Basin Tunguss Basin (in millimetres per year) 3.038 1.664 Aquifer System where groundwater levels are increasing Northern Great Ogallala Aquifer Cambro-Ordovician Russian Platform Basin (in millimetres per year) 4.011 Yakut Basin Plains Aquifer (High Plains) Aquifer System 2.888 Map based on data collected by 4.954 0.309 2.449 NASA's Grace satellite between 2003 and 2013 Paris Basin 4.118 Angara-Lena Basin 3.993 West Siberian Basin Californian Central Atlantic and Gulf Coastal 1.978 Valley Aquifer System Plains Aquifer 8.887 5.932 Tarim Basin Song-Liao Basin North Caucasus Basin 0.232 2.4 Northwestern Sahara Aquifer System 16.097 Why aquifers are important 2.805 Nubian Aquifer System 2.906 North China Aquifer System Only three per cent of the world's water -

Regional Groundwater Modeling of the Guarani Aquifer System
water Article Regional Groundwater Modeling of the Guarani Aquifer System Roger D. Gonçalves 1 , Elias H. Teramoto 1 and Hung K. Chang 2,* 1 Center for Environmental Studies and Basin Studies Laboratory, São Paulo State University, UNESP, Rio Claro, SP 13506-900, Brazil; [email protected] (R.D.G.); [email protected] (E.H.T.) 2 Department of Applied Geology and Basin Studies Laboratory, São Paulo State University, UNESP, Rio Claro, SP 13506-900, Brazil * Correspondence: [email protected] Received: 9 July 2020; Accepted: 17 August 2020; Published: 19 August 2020 Abstract: The Guarani Aquifer System (GAS) is a strategic transboundary aquifer system shared by Brazil, Argentina, Paraguay and Uruguay. This article presents a groundwater flow model to assess the GAS system in terms of regional flow patterns, water balance and overall recharge. Despite the continental dimension of GAS, groundwater recharge is restricted to narrow outcrop zones. An important part is discharged into local watersheds, whereas a minor amount reaches the confined part. A three-dimensional finite element groundwater-flow model of the entire GAS system was constructed to obtain a better understanding of the prevailing flow dynamics and more reliable estimates of groundwater recharge. Our results show that recharge rates effectively contributing to the regional GAS water balance are only approximately 0.6 km3/year (about 4.9 mm/year). These rates are much smaller than previous estimates, including of deep recharge approximations commonly used for water resources management. Higher recharge rates were also not compatible with known 81Kr groundwater age estimates, as well as with calculated residence times using a particle tracking algorithm. -

Groundwater and Global Change: Trends, Opportunities and Challenges
SIDE PUBLICATIONS SERIES :01 Groundwater and Global Change: Trends, Opportunities and Challenges Jac van der Gun UNITED NATIONS WORLD WATER ASSESSMENT PROGRAMME Published in 2012 by the United Nations Educational, Scientific and Cultural Organization 7, Place de Fontenoy, 75352 Paris 07 SP, France © UNESCO 2012 All rights reserved ISBN 978-92-3-001049-2 The designations employed and the presentation of material throughout this publication do not imply the expression of any opinion whatsoever on the part of UNESCO concerning the legal status of any country, territory, city or area or of its authorities, or concerning the delimitation of its frontiers or boundaries. The ideas and opinions expressed in this publication are those of the authors; they are not necessarily those of UNESCO and do not commit the Organization. Photographs: Cover: © africa924 / Shutterstock © Rolffimages / Dreamstime © Frontpage / Shutterstock.com p.i: © holgs / iStockphoto p.ii: © Andrew Zarivny p.2: © Aivolie / Shutterstock p.4: © Jorg Hackemann / Shutterstock p.17: © Jac van der Gun p.31: © Aivolie / Shutterstock p.33: © Hilde Vanstraelen Original concept (cover and layout design) of series: MH Design / Maro Haas Layout: Pica Publishing LTD, London–Paris / Roberto Rossi Printed by: UNESCO Printed in France Groundwater and global change: Trends, opportunities and challenges Author: Jac van der Gun Contributors: Luiz Amore (National Water Agency, Brazil), Greg Christelis (Ministry of Agriculture, Water and Forestry, Nambia), Todd Jarvis (Oregon State University, USA), Neno Kukuric (UNESCO-IGRAC) Júlio Thadeu Kettelhut (Ministry of the Environment, Brazil), Alexandros Makarigakis (UNESCO, Ethiopia), Abdullah Abdulkader Noaman (Sana’a University, Yemen), Cheryl van Kempen (UNESCO-IGRAC), Frank van Weert (UNESCO-IGRAC). -

1 Conflict Risk Indicators Around the Guarani Aquifer
CONFLICT RISK INDICATORS AROUND THE GUARANI AQUIFER SYSTEM Mohamed Redha MENANI1 Harrysson Luiz da Silva2 Ivana Lucia Franco Cei3 Luciana Ribeiro Lepri4 1 - Earth Sciences Dept – Batna University – Algeria - [email protected] 2 - Departamento de Geociencias Universidade Federal de Santa Catarina – UFSC – Brazil 3 - Ministério Público do Estado do Amapá - Brazil 4 - Ministério Público do Estado do Paraná - Brazil Abstract Among achievements related to the environmental protection and sustainable development of the Guarani aquifer system (GAS) project (World Bank, 2009), it was developed a framework for analyzing and classifying causes of critical issues and possible mitigation measures in a transboundary diagnostic analysis. The classified causes recognised are: natural (caused by climate change for example), primary or technical (related inter alia to low level sanitation coverage), secondary or economic management (uncontrolled use of the GAS…), tertiary or political (lack of legal norms or absence of managing institutions) and fundamental or socio-cultural (lack of public participation…). Some of these causes of critical issues resemble to the indicators or sub-indicators proposed in the evaluation method of the conflict risk's index around the transboundary water resources (Menani, 2009); method which will be tested here on the GAS’s case. In August 2010, the four countries signed the Guarani Aquifer System Agreement under the framework of MERCOSUR. Through this action, it is expected a better coordination and a joint management of this strategic shared aquifer. The current GAS data, rather reassuring, don’t mean that there isn't or that there wouldn’t be a risk of conflict about this cross-border aquifer. -

Environment Management Manual
Procedure Document No. 2617 Document Title Environment Management Manual Area HSE Issue Date 23 August 2017 Major Process Environment Sub Process Management Review Authoriser Jacqui McGill – Asset President Version Number 16 Olympic Dam 1 INTRODUCTION ............................................................................................................................ 3 1.1 Glossary and defined terms ................................................................................................. 3 1.2 Purpose and scope .............................................................................................................. 3 1.3 How to use the EPMP .......................................................................................................... 4 2 REGULATORY FRAMEWORK ..................................................................................................... 5 2.1 Key legal requirements ........................................................................................................ 5 2.2 Compliance with routine reporting obligations ..................................................................... 6 2.3 Amendments to the EPMP ................................................................................................... 6 2.4 Environmental outcomes and criteria .................................................................................. 7 2.5 Enforcement process (Indenture and Mining Code) ............................................................ 7 2.6 ALARA and best practicable -

Supplement of Earth Syst
Supplement of Earth Syst. Dynam., 11, 755–774, 2020 https://doi.org/10.5194/esd-11-755-2020-supplement © Author(s) 2020. This work is distributed under the Creative Commons Attribution 4.0 License. Supplement of Groundwater storage dynamics in the world’s large aquifer systems from GRACE: uncertainty and role of extreme precipitation Mohammad Shamsudduha and Richard G. Taylor Correspondence to: Mohammad Shamsudduha ([email protected]) The copyright of individual parts of the supplement might differ from the CC BY 4.0 License. Supplementary Table S1. Characteristics of the world’s 37 large aquifer systems according to the WHYMAP database including aquifer area, total number of population, proportion of groundwater (GW)-fed irrigation, mean aridity index, mean annual rainfall, variability in rainfall and total terrestrial water mass (ΔTWS), and correlation coefficients between monthly ΔTWS and precipitation with reported lags. ) 2 2) Correlation between between Correlation precipitation TWS and (lag in month) GW irrigation (%) (%) GW irrigation on based zones Climate Aridity indices Mean (2002-16) annual precipitation (mm) Rainfall variability (%) (cm TWS variance WHYMAP aquifer number name Aquifer Continent (million)Population area (km Aquifer Nubian Sandstone Hyper- 1 Africa 86.01 2,176,068 1.6 30 12.1 1.5 0.16 (13) Aquifer System arid Northwestern 2 Sahara Aquifer Africa 5.93 1,007,536 4.4 Arid 69 17.3 1.9 0.19 (8) System Murzuk-Djado Hyper- 3 Africa 0.35 483,817 2.3 8 36.6 1.3 0.20 (-8) Basin arid Taoudeni- Hyper- 4 Africa 0.35 -

Walking on Water- Global Aquifers
16 March 2011 Walking on Water Mendel Khoo Researcher FDI Global Food and Water Crises Research Programme Gary Kleyn Manager FDI Global Food and Water Crises Research Programme Summary Aquifers play a key role in the provision of water for farming and for consumption by animals and humans. Almost all parts of the global landmass hide a subterranean water body. Aquifers are underground beds or layers of permeable rock, sediment or soil where water is lodged and can be accessed to yield water. This paper explores some of the major aquifers around the world and determines how countries are coping with increased water usage. Analysis Studying aquifers presents a number of problems, in part because scientists are yet to develop a complete picture of the globe’s aquifer systems; the sub-surface geology still holds mysteries. Further discoveries of aquifers and information on their connectivity with surface water can be expected in the future. The process should be similar to the way in which new discoveries of energy sources beneath the earth’s surface are still being made. An additional impediment lies in the different terms used to describe aquifers, some of them arising simply because of language differences. Aquifers do not fit into one neat category, as there are many variations to their form. The terminology for aquifers can include: underground water basins; groundwater mounds; lakes and parts of rivers; as well as artesian basins, which are confined aquifers contained under positive pressure. Hence, aquifers are not only located underground but some, or all, parts may also be found on the surface.