DOCSLIB.ORG

Vortex Lines Within Low-Level Mesocyclones Obtained From

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Vortex Lines Within Low-Level Mesocyclones Obtained From SEPTEMBER 2008 MARKOWSKI ET AL. 3513 Vortex Lines within Low-Level Mesocyclones Obtained from Pseudo-Dual-Doppler Radar Observations ϩ PAUL MARKOWSKI,* ERIK RASMUSSEN, JERRY STRAKA,# ROBERT DAVIES-JONES,@ YVETTE RICHARDSON,* AND ROBERT J. TRAPP& *Department of Meteorology, The Pennsylvania State University, University Park, Pennsylvania ϩRasmussen Systems, Mesa, Colorado #School of Meteorology, University of Oklahoma, Norman, Oklahoma @National Severe Storms Laboratory, Norman, Oklahoma &Department of Earth and Atmospheric Sciences, Purdue University, West Lafayette, Indiana (Manuscript received 24 July 2007, in final form 4 January 2008) ABSTRACT Vortex lines passing through the low-level mesocyclone regions of six supercell thunderstorms (three nontornadic, three tornadic) are computed from pseudo-dual-Doppler airborne radar observations ob- tained during the Verification of the Origins of Rotation in Tornadoes Experiment (VORTEX). In every case, at least some of the vortex lines emanating from the low-level mesocyclones form arches, that is, they extend vertically from the cyclonic vorticity maximum, then turn horizontally (usually toward the south or southwest) and descend into a broad region of anticyclonic vertical vorticity. This region of anticyclonic vorticity is the same one that has been observed almost invariably to accompany the cyclonic vorticity maximum associated with the low-level mesocyclone; the vorticity couplet straddles the hook echo of the supercell thunderstorm. The arching of the vortex lines and the orientation of the vorticity vector along the vortex line arches, compared to the orientation of the ambient (barotropic) vorticity, are strongly suggestive of baroclinic vorticity generation within the hook echo and associated rear-flank downdraft region of the supercells, and subsequent lifting of the baroclinically altered/generated vortex lines by an updraft. Dis- cussion on the generality of these findings, possible implications for tornadogenesis, and the similarity of the observed vortex lines to vortex lines in larger-scale convective systems are included as well. 1. Introduction ponent at a time. For example, the dynamics of midlevel mesocyclogenesis in supercell thunderstorms Vortex lines (also sometimes called vortex filaments) is easily demonstrated by way of vortex lines (Davies- are lines tangent to the vorticity vector, analogous to Jones 1984; Rotunno and Klemp 1985; Fig. 1). Vortex the streamline in a velocity vector field (Dutton 1986, p. line analyses in phenomena like thunderstorms are 364; Pedlosky 1987, p. 25; Kundu 1990, p. 120).1 Vortex complicated by the baroclinic generation of vorticity by lines can aid the visualization of the three-dimensional the horizontal buoyancy gradients that accompany pre- vorticity field. The three-dimensional perspective pro- cipitation regions and vertical drafts. In the presence of vided by vortex lines can expose dynamics that may not significant baroclinic vorticity generation, vortex lines be as apparent in inspections of only one vorticity com- may not even closely approximate material lines (Helmholtz’ theorem). Nonetheless, vortex line analy- ses can be enlightening in that they can suggest plau- 1 What are referred to as “vortex lines” herein are termed “vor- sible methods of vorticity generation and reorientation ticity lines” by Lugt (1996, p. 90). Lugt defines a vortex line as an (e.g., observations of vortex rings might lead one to isolated vorticity line within a wind field that is otherwise irrota- surmise that a local buoyancy extremum is present and tional. responsible for the generation of the rings). Although the vertical component of vorticity tends to be empha- Corresponding author address: Dr. Paul Markowski, 503 sized in supercell thunderstorm and tornado studies, Walker Building, University Park, PA 16802. there is some merit in systematically inspecting the dis- E-mail: [email protected] tribution and orientation of three-dimensional vortex DOI: 10.1175/2008MWR2315.1 © 2008 American Meteorological Society Unauthenticated | Downloaded 09/27/21 04:08 AM UTC MWR2315 3514 MONTHLY WEATHER REVIEW VOLUME 136 FIG. 1. (a) Effect of a localized vertical displacement “peak” (i.e., hump in an isentropic surface) on vortex lines when the mean vorticity ␻ and mean storm-relative flow v Ϫ c are perpendicular (purely crosswise vorticity). The peak draws up loops of vortex lines (shown slightly above, instead of in, the surface for clarity), giving rise to cyclonic vorticity on the right side of the peak (relative to the shear vector S) and anticyclonic vorticity on the left side. [Solenoidal effects (not included in the drawing) actually divert the vortex lines around the right (left) side of a warm (cool) peak, relative to the mean vorticity vector, but do not alter the result.] The environmental flow across the expanding peak produces maximum updraft upstream (storm-relative frame) of the peak due to the upslope component of the vertical velocity. In this case, there is no correlation between vertical velocity and vertical vorticity. (b) As in (a), but for the other extreme when vorticity is purely streamwise (i.e., ␻ is parallel to v Ϫ c). Here, the upslope (downslope) side of the peak is also the cyclonic (anticyclonic) side, and the vertical velocity and vertical vorticity are positive correlated. (From Davies-Jones 1984.) lines in observed and simulated storms. A lengthier dis- wind fields) with the exception of the recent supercell cussion on the benefits of vortex line analysis appears in thunderstorm studies by Majcen et al. (2006) and Straka et al. (2007). Straka et al. (2007). Vortex line analyses appear relatively infrequently The origins of midlevel and low-level rotation in su- within the body of severe local storms literature. In percell thunderstorms have been reviewed by Davies- addition to the previously cited theoretical and numeri- Jones and Brooks (1993), Rotunno (1993), and Davies- cal modeling studies of midlevel mesocyclogenesis by Jones et al. (2001). [Herein, “low level” refers to alti- Davies-Jones (1984) and midlevel and low-level meso- tudes nominally Յ1000 m AGL. Davies-Jones et al. cyclogenesis by Rotunno and Klemp (1985), respec- (2001) referred to these altitudes as “near ground.” The tively, Walko (1993) and Wicker and Wilhelmson distinction between low-level and midlevel mesocy- (1995) presented vortex lines in their three-dimensional clones is discussed further in section 4.] Midlevel verti- simulations of tornadogenesis. As one would expect, cal vorticity having relatively high correlation with ver- the vortex lines were nearly erect in the tornadoes, tical velocity (negative correlation, in the case of a “left- turned horizontally at the base of the tornadoes, and moving” storm)—what most would probably consider then extended horizontally several kilometers from the the defining characteristic of a supercell thunderstorm tornadoes along the surface. Weisman and Davis (1998) (i.e., a rotating updraft)—can be envisioned as arising presented vortex lines in their investigation of the gen- from the tilting of vortex lines having a significant esis of line-end vortices in mesoscale convective sys- streamwise component by an “isentropic mountain” tems. The counterrotating mesoscale vortices com- (Davies-Jones 1984; Fig. 1). The vortex lines are quasi- monly found at opposite ends of quasi-linear convective horizontal in the ambient environment owing to the line segments were joined by “arching” vortex lines that presence of large mean vertical wind shear. On the rose out of the cyclonic vortex to the north (in the case other hand, baroclinic vorticity generation is present in of westerly mean vertical shear and a north–south con- convective storms, at least somewhere, owing to the vective line orientation), turned horizontally and ex- presence of horizontal buoyancy gradients (if there tended many tens of kilometers to the south, and then were no buoyancy gradients there could be no buoyant descended into the anticyclonic vortex. More recently, updraft in the first place). In addition to the updraft, the Nolan (2004) showed that three-dimensional Lagran- evaporation of rain, the melting of graupel and hail, and gian vortex methods (Chorin 1996) could be used to even the direct contribution to negative buoyancy by simulate mesocyclogenesis as an alternative to the tra- the mass of hydrometeors themselves unavoidably lead ditional approach of simulating the dynamics with an to horizontal buoyancy gradients and baroclinic vortic- Eulerian grid. We are unaware of any attempts to con- ity generation. Given this addition of baroclinic vortic- struct vortex lines in observed convective storms (using ity (Dutton 1986, p. 390; Davies-Jones 1996; Davies- presumably dual-Doppler–derived three-dimensional Jones et al. 2001) to the barotropic vorticity (defined as Unauthenticated | Downloaded 09/27/21 04:08 AM UTC SEPTEMBER 2008 MARKOWSKI ET AL. 3515 the vorticity that has resulted from the amplification storm-scale horizontal vorticity and is crucial for the and reorientation of the initial ambient vorticity of the development of low-level mesocyclones (Klemp and vertically sheared environment over the lifetime of the Rotunno 1983; Rotunno and Klemp 1985) [although storm), particularly at low levels within the rain-cooled recent observations (e.g., Shabbott and Markowski outflow of storms where significant buoyancy gradients 2006; Beck et al. 2006; Frame et al. 2008) have raised would most likely be found [prior modeling
Load more

Recommended publications
  • From Improving Tornado Warnings: from Observation to Forecast
    Improving Tornado Warnings: from Observation to Forecast John T. Snow Regents’ Professor of Meteorology Dean Emeritus, College of Atmospheric and Geographic Sciences, The University of Oklahoma Major contributions from: Dr. Russel Schneider –NOAA Storm Prediction Center Dr. David Stensrud – NOAA National Severe Storms Laboratory Dr. Ming Xue –Center for Analysis and Prediction of Storms, University of Oklahoma Dr. Lou Wicker –NOAA National Severe Storms Laboratory Hazards Caucus Alliance Briefing Tornadoes: Understanding how they develop and providing early warning 10:30 am – 11:30 am, Wednesday, 21 July 2010 Senate Capitol Visitors Center 212 Each Year: ~1,500 tornadoes touch down in the United States, causing over 80 deaths, 100s of injuries, and an estimated $1.1 billion in damages Statistics from NOAA Storm Prediction Center Supercell –A long‐lived rotating thunderstorm the primary type of thunderstorm producing strong and violent tornadoes Present Warning System: Warn on Detection • A Warning is the culmination of information developed and distributed over the preceding days sequence of day‐by‐day forecasts identifies an area of high threat •On the day, storm spotters deployed; radars monitor formation, growth of thunderstorms • Appearance of distinct cloud or radar echo features tornado has formed or is about to do so Warning is generated, distributed Present Warning System: Warn on Detection Radar at 2100 CST Radar at 2130 CST with Warning Thunderstorms are monitored using radar A warning is issued based on the detected and
    [Show full text]
  • Downloaded 09/30/21 06:43 PM UTC JUNE 1996 MONTEVERDI and JOHNSON 247
    246 WEATHER AND FORECASTING VOLUME 11 A Supercell Thunderstorm with Hook Echo in the San Joaquin Valley, California JOHN P. MONTEVERDI Department of Geosciences, San Francisco State University, San Francisco, California STEVE JOHNSON Association of Central California Weather Observers, Fresno, California (Manuscript received 30 January 1995, in ®nal form 9 February 1996) ABSTRACT This study documents a damaging supercell thunderstorm that occurred in California's San Joaquin Valley on 5 March 1994. The storm formed in a ``cold sector'' environment similar to that documented for several other recent Sacramento Valley severe thunderstorm events. Analyses of hourly subsynoptic surface and radar data suggested that two thunderstorms with divergent paths developed from an initial echo that had formed just east of the San Francisco Bay region. The southern storm became severe as it ingested warmer, moister boundary layer air in the south-central San Joaquin Valley. A well-developed hook echo with a 63-dBZ core was observed by a privately owned 5-cm radar as the storm passed through the Fresno area. Buoyancy parameters and ho- dograph characteristics were obtained both for estimated conditions for Fresno [on the basis of a modi®ed morning Oakland (OAK) sounding] and for the actual storm environment (on the basis of a radiosonde launched from Lemoore Naval Air Station at about the time of the storm's passage through the Fresno area). Both the estimated and actual hodographs essentially were straight and suggested storm splitting. Although the actual CAPE was similar to that which was estimated, the observed magnitude of the low-level shear was considerably greater than the estimate.
    [Show full text]
  • ESSENTIALS of METEOROLOGY (7Th Ed.) GLOSSARY
    ESSENTIALS OF METEOROLOGY (7th ed.) GLOSSARY Chapter 1 Aerosols Tiny suspended solid particles (dust, smoke, etc.) or liquid droplets that enter the atmosphere from either natural or human (anthropogenic) sources, such as the burning of fossil fuels. Sulfur-containing fossil fuels, such as coal, produce sulfate aerosols. Air density The ratio of the mass of a substance to the volume occupied by it. Air density is usually expressed as g/cm3 or kg/m3. Also See Density. Air pressure The pressure exerted by the mass of air above a given point, usually expressed in millibars (mb), inches of (atmospheric mercury (Hg) or in hectopascals (hPa). pressure) Atmosphere The envelope of gases that surround a planet and are held to it by the planet's gravitational attraction. The earth's atmosphere is mainly nitrogen and oxygen. Carbon dioxide (CO2) A colorless, odorless gas whose concentration is about 0.039 percent (390 ppm) in a volume of air near sea level. It is a selective absorber of infrared radiation and, consequently, it is important in the earth's atmospheric greenhouse effect. Solid CO2 is called dry ice. Climate The accumulation of daily and seasonal weather events over a long period of time. Front The transition zone between two distinct air masses. Hurricane A tropical cyclone having winds in excess of 64 knots (74 mi/hr). Ionosphere An electrified region of the upper atmosphere where fairly large concentrations of ions and free electrons exist. Lapse rate The rate at which an atmospheric variable (usually temperature) decreases with height. (See Environmental lapse rate.) Mesosphere The atmospheric layer between the stratosphere and the thermosphere.
    [Show full text]
  • Tornadogenesis in a Simulated Mesovortex Within a Mesoscale Convective System
    3372 JOURNAL OF THE ATMOSPHERIC SCIENCES VOLUME 69 Tornadogenesis in a Simulated Mesovortex within a Mesoscale Convective System ALEXANDER D. SCHENKMAN,MING XUE, AND ALAN SHAPIRO Center for Analysis and Prediction of Storms, and School of Meteorology, University of Oklahoma, Norman, Oklahoma (Manuscript received 3 February 2012, in final form 23 April 2012) ABSTRACT The Advanced Regional Prediction System (ARPS) is used to simulate a tornadic mesovortex with the aim of understanding the associated tornadogenesis processes. The mesovortex was one of two tornadic meso- vortices spawned by a mesoscale convective system (MCS) that traversed southwestern and central Okla- homa on 8–9 May 2007. The simulation used 100-m horizontal grid spacing, and is nested within two outer grids with 400-m and 2-km grid spacing, respectively. Both outer grids assimilate radar, upper-air, and surface observations via 5-min three-dimensional variational data assimilation (3DVAR) cycles. The 100-m grid is initialized from a 40-min forecast on the 400-m grid. Results from the 100-m simulation provide a detailed picture of the development of a mesovortex that produces a submesovortex-scale tornado-like vortex (TLV). Closer examination of the genesis of the TLV suggests that a strong low-level updraft is critical in converging and amplifying vertical vorticity associated with the mesovortex. Vertical cross sections and backward trajectory analyses from this low-level updraft reveal that the updraft is the upward branch of a strong rotor that forms just northwest of the simulated TLV. The horizontal vorticity in this rotor originates in the near-surface inflow and is caused by surface friction.
    [Show full text]
  • Near-Surface Vortex Structure in a Tornado and in a Sub-Tornado-Strength Convective-Storm Vortex Observed by a Mobile, W-Band Radar During VORTEX2
    VOLUME 141 MONTHLY WEATHER REVIEW NOVEMBER 2013 Near-Surface Vortex Structure in a Tornado and in a Sub-Tornado-Strength Convective-Storm Vortex Observed by a Mobile, W-Band Radar during VORTEX2 ,1 # @ ROBIN L. TANAMACHI,* HOWARD B. BLUESTEIN, MING XUE,* WEN-CHAU LEE, & & @ KRZYSZTOF A. ORZEL, STEPHEN J. FRASIER, AND ROGER M. WAKIMOTO * Center for Analysis and Prediction of Storms, and School of Meteorology, University of Oklahoma, Norman, Oklahoma # School of Meteorology, University of Oklahoma, Norman, Oklahoma @ National Center for Atmospheric Research, Boulder, Colorado & Microwave Remote Sensing Laboratory, University of Massachusetts, Amherst, Amherst, Massachusetts (Manuscript received 14 November 2012, in final form 22 May 2013) ABSTRACT As part of the Second Verification of the Origins of Rotation in Tornadoes Experiment (VORTEX2) field campaign, a very high-resolution, mobile, W-band Doppler radar collected near-surface (#200 m AGL) observations in an EF-0 tornado near Tribune, Kansas, on 25 May 2010 and in sub-tornado-strength vortices near Prospect Valley, Colorado, on 26 May 2010. In the Tribune case, the tornado’s condensation funnel dissipated and then reformed after a 3-min gap. In the Prospect Valley case, no condensation funnel was observed, but evidence from the highest-resolution radars in the VORTEX2 fleet indicates multiple, sub-tornado-strength vortices near the surface, some with weak-echo holes accompanying Doppler velocity couplets. Using high-resolution Doppler radar data, the authors document the full life cycle of sub- tornado-strength vortex beneath a convective storm that previously produced tornadoes. The kinematic evolution of these vortices, from genesis to decay, is investigated via ground-based velocity track display (GBVTD) analysis of the W-band velocity data.
    [Show full text]
  • The Origins of Vortex Sheets in a Simulated Supercell Thunderstorm
    3944 MONTHLY WEATHER REVIEW VOLUME 142 The Origins of Vortex Sheets in a Simulated Supercell Thunderstorm PAUL MARKOWSKI AND YVETTE RICHARDSON Department of Meteorology, The Pennsylvania State University, University Park, Pennsylvania GEORGE BRYAN Mesoscale and Microscale Meteorology Division, National Center for Atmospheric Research, Boulder, Colorado (Manuscript received 23 May 2014, in final form 16 July 2014) ABSTRACT This paper investigates the origins of the (cyclonic) vertical vorticity within vortex sheets that develop within a numerically simulated supercell in a nonrotating, horizontally homogeneous environment with a free-slip lower boundary. Vortex sheets are commonly observed along the gust fronts of supercell storms, particularly in the early stages of storm development. The ‘‘collapse’’ of a vortex sheet into a compact vortex is often seen to accompany the intensification of rotation that occasionally leads to tornadogenesis. The vortex sheets predominantly acquire their vertical vorticity from the tilting of horizontal vorticity that has been modified by horizontal buoyancy gradients associated with the supercell’s cool low-level outflow. If the tilting is within an ascending airstream (i.e., the horizontal gradient of vertical velocity responsible for the tilting resides entirely within an updraft), the vertical vorticity of the vortex sheet nearly vanishes at the lowest model level for horizontal winds (5 m). However, if the tilting occurs within a descending airstream (i.e., the hori- zontal gradient of vertical velocity responsible for tilting includes a downdraft adjacent to the updraft within which the majority of the cyclonic vorticity resides), the vortex sheet extends to the lowest model level. The findings are consistent with the large body of prior work that has found that downdrafts are necessary for the development of significant vertical vorticity at the surface.
    [Show full text]
  • Radar Artifacts and Associated Signatures, Along with Impacts of Terrain on Data Quality
    Radar Artifacts and Associated Signatures, Along with Impacts of Terrain on Data Quality 1.) Introduction: The WSR-88D (Weather Surveillance Radar designed and built in the 80s) is the most useful tool used by National Weather Service (NWS) Meteorologists to detect precipitation, calculate its motion, estimate its type (rain, snow, hail, etc) and forecast its position. Radar stands for “Radio, Detection, and Ranging”, was developed in the 1940’s and used during World War II, has gone through numerous enhancements and technological upgrades to help forecasters investigate storms with greater detail and precision. However, as our ability to detect areas of precipitation, including rotation within thunderstorms has vastly improved over the years, so has the radar’s ability to detect other significant meteorological and non meteorological artifacts. In this article we will identify these signatures, explain why and how they occur and provide examples from KTYX and KCXX of both meteorological and non meteorological data which WSR-88D detects. KTYX radar is located on the Tug Hill Plateau near Watertown, NY while, KCXX is located in Colchester, VT with both operated by the NWS in Burlington. Radar signatures to be shown include: bright banding, tornadic hook echo, low level lake boundary, hail spikes, sunset spikes, migrating birds, Route 7 traffic, wind farms, and beam blockage caused by terrain and the associated poor data sampling that occurs. 2.) How Radar Works: The WSR-88D operates by sending out directional pulses at several different elevation angles, which are microseconds long, and when the pulse intersects water droplets or other artifacts, a return signal is sent back to the radar.
    [Show full text]
  • A Revised Tornado Definition and Changes in Tornado Taxonomy
    1256 WEATHER AND FORECASTING VOLUME 29 A Revised Tornado Definition and Changes in Tornado Taxonomy ERNEST M. AGEE Department of Earth, Atmospheric, and Planetary Sciences, Purdue University, West Lafayette, Indiana (Manuscript received 4 June 2014, in final form 30 July 2014) ABSTRACT The tornado taxonomy presented by Agee and Jones is revised to account for the new definition of a tor- nado provided by the American Meteorological Society (AMS) in October 2013, resulting in the elimination of shear-driven vortices from the taxonomy, such as gustnadoes and vortices in the eyewall of hurricanes. Other relevant research findings since the initial issuance of the taxonomy are also considered and in- corporated, where appropriate, to help improve the classification system. Multiple misoscale shear-driven vortices in a single tornado event, when resulting from an inertial instability, are also viewed to not meet the definition of a tornado. 1. Introduction and considerations from a cumuliform cloud, and often visible as a funnel cloud and/or circulating debris/dust at the ground.’’ In The first proposed tornado taxonomy was presented view of the latest definition, a few changes are warranted by Agee and Jones (2009, hereafter AJ) consisting of in the AJ taxonomy. Considering the roles played by three types and 15 species, ranging from the type I buoyancy and shear on a variety of spatial and temporal (potentially strong and violent) tornadoes produced by scales (from miso to meso to synoptic), coupled with the the classic supercell, to the more benign type III con- requirement in the latest definition that a tornado must vective and shear-driven vortices such as landspouts and be pendant from a cumuliform cloud, it is necessary to gustnadoes.
    [Show full text]
  • Version 3.0) VORTEX2 Domain Multiple Ground Bases Approved for 2009-10
    VORTEX 2 (Version 3.0) VORTEX2 domain multiple ground bases Approved for 2009-10 Sioux City www.vortex2.org for updates Boulder NCAR Steering committee: CSWR Hays Howie Bluestein, OU Don Burgess, CIMMS Norman NSSL David Dowell, NCAR OU Paul Markowski, PSU Lub b o c k Erik Rasmussen, CIMMS Yvette Richardson, PSU Lou Wicker, NSSL Joshua Wurman, CSWR Rapid-Scan DOW SMART-Radar UAV DOW NOXP (XPOL) W-Band Fig. 3.2 RECUV UAV being readied for flight. A variety of instruments, focusing on mesoscale observations, radar, and direct T, RH, wind (others likely to be proposed too) Probes Sticknet DOWs Mesonets Tethered pre-storm Tethered Phase, in OK K V N 4/1-5/10 X KT Takes advantage of LX stationary assets like the Norman Phased-Array 0 25 km CASA, etc. N K O U (fixed radars not shown in order to improve clarity) K F WSR-88D dual- NWRT-PAR CASA mobile radar D coverage polarimetric coverage at X-band radar coverage at stick net R at 1 km AGL WSR-88D 1 km AGL coverage at 250 m AGL Oklahoma coverage 250 m AGL Studies larger mesoscale at 1 km AGL TDWR fixed site mobile Texas coverage at Oklahoma Ft. Cobb Little Washita rawinsonde rawinsonde 250 m AGL mesonet ARS micronet ARS micronet 0 50 100 km site ASOS wind profiler mobile mesonet UAV Cell merger precipitation gust front K supercell forward flank region V N X anvil edge KT LX precipitation gust front 0 5km K O U N (radars not shown in order to improve clarity) K F WSR-88D dual- NWRT-PAR CASA mobile radar D coverage polarimetric coverage at X-band radar coverage at stick net at 1 km AGL WSR-88D 1 km AGL coverage at R 250 m AGL Oklahoma coverage 250 m AGL at 1 km AGL TDWR fixed site mobile Texas coverage at Oklahoma Ft.
    [Show full text]
  • Glossary of Severe Weather Terms
    Glossary of Severe Weather Terms -A- Anvil The flat, spreading top of a cloud, often shaped like an anvil. Thunderstorm anvils may spread hundreds of miles downwind from the thunderstorm itself, and sometimes may spread upwind. Anvil Dome A large overshooting top or penetrating top. -B- Back-building Thunderstorm A thunderstorm in which new development takes place on the upwind side (usually the west or southwest side), such that the storm seems to remain stationary or propagate in a backward direction. Back-sheared Anvil [Slang], a thunderstorm anvil which spreads upwind, against the flow aloft. A back-sheared anvil often implies a very strong updraft and a high severe weather potential. Beaver ('s) Tail [Slang], a particular type of inflow band with a relatively broad, flat appearance suggestive of a beaver's tail. It is attached to a supercell's general updraft and is oriented roughly parallel to the pseudo-warm front, i.e., usually east to west or southeast to northwest. As with any inflow band, cloud elements move toward the updraft, i.e., toward the west or northwest. Its size and shape change as the strength of the inflow changes. Spotters should note the distinction between a beaver tail and a tail cloud. A "true" tail cloud typically is attached to the wall cloud and has a cloud base at about the same level as the wall cloud itself. A beaver tail, on the other hand, is not attached to the wall cloud and has a cloud base at about the same height as the updraft base (which by definition is higher than the wall cloud).
    [Show full text]
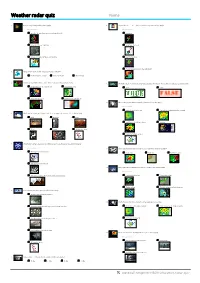
  • Weather Radar Quiz Name
    Weather radar quiz Name: 1. Base velocity displays (select all that apply) 8. Targets that are ____ or ___ have no radial velocity (select all that apply) Select 2 answers Select 2 answers A Speed of the wind toward or away from the radar A stationary B Intensity of the precipitation B away from the radar C Movement of precipitation over the time C towards the radar D moving perpendicular to the radar beam 2. What are the values of reflectivity for precipitation mode? A From -28 dbz to +28 dbz B From 0 to 75 dbz C Above 45 dbz 3. Positive values (warm yellow to red colors) of velocities indicates movements 9. The higher gradient in the reflectivity values between the edge of the cell and core indicates a stronger storm. A perpendicular to the radar beam C towards the radar A True B False B away from the radar D parallel to the radar beam 10. What radar features indicate tropical cyclone? (select all that apply) Select 4 answers A Low reflectivity in the eye D High reflectivity band spiraling outward 4. Which non-meteorological targets can be detected by weather radars? (select all that apply) A Birds C Buildings E Dust B Small and circled shape echoes E Rotation B Trees D Smoke F All from the above C High reflectivity in eyewall 5. What factros enhance the radar reflectivity around the melting level? (select all that apply) Select 2 answers 11. What radar signature indicates that strong, straight-line winds are possible? A The targets become warmer A Hook echo B Bow echo C Rotation couplet B The targets increase in size 12.
    [Show full text]
  • Tornadogenesis: Our Current Understanding, Forecasting Considerations, and Questions to Guide Future Research
    Atmospheric Research 93 (2009) 3–10 Contents lists available at ScienceDirect Atmospheric Research journal homepage: www.elsevier.com/locate/atmos Tornadogenesis: Our current understanding, forecasting considerations, and questions to guide future research Paul M. Markowski ⁎, Yvette P. Richardson Department of Meteorology, Pennsylvania State University, University Park, PA, United States article info abstract Article history: This paper reviews our present understanding of tornadogenesis and some of the outstanding Received 30 November 2007 questions that remain. The emphasis is on tornadogenesis within supercell thunderstorms. The Received in revised form 30 June 2008 origin of updraft-scale rotation, i.e., mesocyclogenesis, above the ground is reviewed first, Accepted 19 September 2008 followed by the requisites for the development of rotation near the ground. Forecasting strategies also are discussed, and some speculations are made about the relationships between Keywords: the dynamics of tornadogenesis and the forecasting parameters that have been somewhat Supercell successful discriminators between tornadic and nontornadic supercells. Thunderstorm Tornado When preexisting rotation is absent at the ground, a downdraft is required for tornadogenesis. Tornadogenesis Not surprisingly, decades of tornado observations and supercell simulations have revealed Mesocyclone that downdrafts are present in close proximity to tornadoes and significant nontornadic Mesocyclogenesis vortices at the surface. Tornadic supercells are favored when the outflow associated with Downdraft downdrafts is not too negatively buoyant. Cold outflow may inhibit vorticity stretching and/or lead to updrafts that are undercut by their own outflow. It may be for this reason that climatological studies of supercell environments have found that the likelihood of tornadic supercells increases as the environmental, boundary layer relative humidity increases (there is some tendency for supercell outflow to be less negatively buoyant in relatively humid environments).
    [Show full text]