Projects and Publications of the Applied Mathematics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Classical and Modern Diffraction Theory
Downloaded from http://pubs.geoscienceworld.org/books/book/chapter-pdf/3701993/frontmatter.pdf by guest on 29 September 2021 Classical and Modern Diffraction Theory Edited by Kamill Klem-Musatov Henning C. Hoeber Tijmen Jan Moser Michael A. Pelissier SEG Geophysics Reprint Series No. 29 Sergey Fomel, managing editor Evgeny Landa, volume editor Downloaded from http://pubs.geoscienceworld.org/books/book/chapter-pdf/3701993/frontmatter.pdf by guest on 29 September 2021 Society of Exploration Geophysicists 8801 S. Yale, Ste. 500 Tulsa, OK 74137-3575 U.S.A. # 2016 by Society of Exploration Geophysicists All rights reserved. This book or parts hereof may not be reproduced in any form without permission in writing from the publisher. Published 2016 Printed in the United States of America ISBN 978-1-931830-00-6 (Series) ISBN 978-1-56080-322-5 (Volume) Library of Congress Control Number: 2015951229 Downloaded from http://pubs.geoscienceworld.org/books/book/chapter-pdf/3701993/frontmatter.pdf by guest on 29 September 2021 Dedication We dedicate this volume to the memory Dr. Kamill Klem-Musatov. In reading this volume, you will find that the history of diffraction We worked with Kamill over a period of several years to compile theory was filled with many controversies and feuds as new theories this volume. This volume was virtually ready for publication when came to displace or revise previous ones. Kamill Klem-Musatov’s Kamill passed away. He is greatly missed. new theory also met opposition; he paid a great personal price in Kamill’s role in Classical and Modern Diffraction Theory goes putting forth his theory for the seismic diffraction forward problem. -

Intensity of Double-Slit Pattern • Three Or More Slits
• Intensity of double-slit pattern • Three or more slits Practice: Chapter 37, problems 13, 14, 17, 19, 21 Screen at ∞ θ d Path difference Δr = d sin θ zero intensity at d sinθ = (m ± ½ ) λ, m = 0, ± 1, ± 2, … max. intensity at d sinθ = m λ, m = 0, ± 1, ± 2, … 1 Questions: -what is the intensity of the double-slit pattern at an arbitrary position? -What about three slits? four? five? Find the intensity of the double-slit interference pattern as a function of position on the screen. Two waves: E1 = E0 sin(ωt) E2 = E0 sin(ωt + φ) where φ =2π (d sin θ )/λ , and θ gives the position. Steps: Find resultant amplitude, ER ; then intensities obey where I0 is the intensity of each individual wave. 2 Trigonometry: sin a + sin b = 2 cos [(a-b)/2] sin [(a+b)/2] E1 + E2 = E0 [sin(ωt) + sin(ωt + φ)] = 2 E0 cos (φ / 2) cos (ωt + φ / 2)] Resultant amplitude ER = 2 E0 cos (φ / 2) Resultant intensity, (a function of position θ on the screen) I position - fringes are wide, with fuzzy edges - equally spaced (in sin θ) - equal brightness (but we have ignored diffraction) 3 With only one slit open, the intensity in the centre of the screen is 100 W/m 2. With both (identical) slits open together, the intensity at locations of constructive interference will be a) zero b) 100 W/m2 c) 200 W/m2 d) 400 W/m2 How does this compare with shining two laser pointers on the same spot? θ θ sin d = d Δr1 d θ sin d = 2d θ Δr2 sin = 3d Δr3 Total, 4 The total field is where φ = 2π (d sinθ )/λ •When d sinθ = 0, λ , 2λ, .. -

Light and Matter Diffraction from the Unified Viewpoint of Feynman's
European J of Physics Education Volume 8 Issue 2 1309-7202 Arlego & Fanaro Light and Matter Diffraction from the Unified Viewpoint of Feynman’s Sum of All Paths Marcelo Arlego* Maria de los Angeles Fanaro** Universidad Nacional del Centro de la Provincia de Buenos Aires CONICET, Argentine *[email protected] **[email protected] (Received: 05.04.2018, Accepted: 22.05.2017) Abstract In this work, we present a pedagogical strategy to describe the diffraction phenomenon based on a didactic adaptation of the Feynman’s path integrals method, which uses only high school mathematics. The advantage of our approach is that it allows to describe the diffraction in a fully quantum context, where superposition and probabilistic aspects emerge naturally. Our method is based on a time-independent formulation, which allows modelling the phenomenon in geometric terms and trajectories in real space, which is an advantage from the didactic point of view. A distinctive aspect of our work is the description of the series of transformations and didactic transpositions of the fundamental equations that give rise to a common quantum framework for light and matter. This is something that is usually masked by the common use, and that to our knowledge has not been emphasized enough in a unified way. Finally, the role of the superposition of non-classical paths and their didactic potential are briefly mentioned. Keywords: quantum mechanics, light and matter diffraction, Feynman’s Sum of all Paths, high education INTRODUCTION This work promotes the teaching of quantum mechanics at the basic level of secondary school, where the students have not the necessary mathematics to deal with canonical models that uses Schrodinger equation. -

The Path Integral Approach to Quantum Mechanics Lecture Notes for Quantum Mechanics IV
The Path Integral approach to Quantum Mechanics Lecture Notes for Quantum Mechanics IV Riccardo Rattazzi May 25, 2009 2 Contents 1 The path integral formalism 5 1.1 Introducingthepathintegrals. 5 1.1.1 Thedoubleslitexperiment . 5 1.1.2 An intuitive approach to the path integral formalism . .. 6 1.1.3 Thepathintegralformulation. 8 1.1.4 From the Schr¨oedinger approach to the path integral . .. 12 1.2 Thepropertiesofthepathintegrals . 14 1.2.1 Pathintegralsandstateevolution . 14 1.2.2 The path integral computation for a free particle . 17 1.3 Pathintegralsasdeterminants . 19 1.3.1 Gaussianintegrals . 19 1.3.2 GaussianPathIntegrals . 20 1.3.3 O(ℏ) corrections to Gaussian approximation . 22 1.3.4 Quadratic lagrangians and the harmonic oscillator . .. 23 1.4 Operatormatrixelements . 27 1.4.1 Thetime-orderedproductofoperators . 27 2 Functional and Euclidean methods 31 2.1 Functionalmethod .......................... 31 2.2 EuclideanPathIntegral . 32 2.2.1 Statisticalmechanics. 34 2.3 Perturbationtheory . .. .. .. .. .. .. .. .. .. .. 35 2.3.1 Euclidean n-pointcorrelators . 35 2.3.2 Thermal n-pointcorrelators. 36 2.3.3 Euclidean correlators by functional derivatives . ... 38 0 0 2.3.4 Computing KE[J] and Z [J] ................ 39 2.3.5 Free n-pointcorrelators . 41 2.3.6 The anharmonic oscillator and Feynman diagrams . 43 3 The semiclassical approximation 49 3.1 Thesemiclassicalpropagator . 50 3.1.1 VanVleck-Pauli-Morette formula . 54 3.1.2 MathematicalAppendix1 . 56 3.1.3 MathematicalAppendix2 . 56 3.2 Thefixedenergypropagator. 57 3.2.1 General properties of the fixed energy propagator . 57 3.2.2 Semiclassical computation of K(E)............. 61 3.2.3 Two applications: reflection and tunneling through a barrier 64 3 4 CONTENTS 3.2.4 On the phase of the prefactor of K(xf ,tf ; xi,ti) .... -

Opacity Effects on Pulsations of Main-Sequence A-Type Stars
atoms Article Opacity Effects on Pulsations of Main-Sequence A-Type Stars Joyce A. Guzik * ID , Christopher J. Fontes and Chris Fryer ID Los Alamos National Laboratory, Los Alamos, NM 87545, USA; [email protected] (C.J.F.); [email protected] (C.F.) * Correspondence: [email protected] Received: 10 April 2018; Accepted: 11 May 2018 ; Published: 4 June 2018 Abstract: Opacity enhancements for stellar interior conditions have been explored to explain observed pulsation frequencies and to extend the pulsation instability region for B-type main-sequence variable stars. For these stars, the pulsations are driven in the region of the opacity bump of Fe-group elements at ∼200,000 K in the stellar envelope. Here we explore effects of opacity enhancements for the somewhat cooler main-sequence A-type stars, in which p-mode pulsations are driven instead in the second helium ionization region at ∼50,000 K. We compare models using the new LANL OPLIB vs. LLNL OPAL opacities for the AGSS09 solar mixture. For models of two solar masses and effective temperature 7600 K, opacity enhancements have only a mild effect on pulsations, shifting mode frequencies and/or slightly changing kinetic-energy growth rates. Increased opacity near the bump at 200,000 K can induce convection that may alter composition gradients created by diffusive settling and radiative levitation. Opacity increases around the hydrogen and 1st He ionization region (∼13,000 K) can cause additional higher-frequency p modes to be excited, raising the possibility that improved treatment of these layers may result in prediction of new modes that could be tested by observations. -
Simple Cubic Lattice
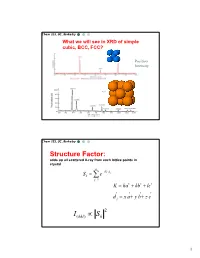
Chem 253, UC, Berkeley What we will see in XRD of simple cubic, BCC, FCC? Position Intensity Chem 253, UC, Berkeley Structure Factor: adds up all scattered X-ray from each lattice points in crystal n iKd j Sk e j1 K ha kb lc d j x a y b z c 2 I(hkl) Sk 1 Chem 253, UC, Berkeley X-ray scattered from each primitive cell interfere constructively when: eiKR 1 2d sin n For n-atom basis: sum up the X-ray scattered from the whole basis Chem 253, UC, Berkeley ' k d k d di R j ' K k k Phase difference: K (di d j ) The amplitude of the two rays differ: eiK(di d j ) 2 Chem 253, UC, Berkeley The amplitude of the rays scattered at d1, d2, d3…. are in the ratios : eiKd j The net ray scattered by the entire cell: n iKd j Sk e j1 2 I(hkl) Sk Chem 253, UC, Berkeley For simple cubic: (0,0,0) iK0 Sk e 1 3 Chem 253, UC, Berkeley For BCC: (0,0,0), (1/2, ½, ½)…. Two point basis 1 2 iK ( x y z ) iKd j iK0 2 Sk e e e j1 1 ei (hk l) 1 (1)hkl S=2, when h+k+l even S=0, when h+k+l odd, systematical absence Chem 253, UC, Berkeley For BCC: (0,0,0), (1/2, ½, ½)…. Two point basis S=2, when h+k+l even S=0, when h+k+l odd, systematical absence (100): destructive (200): constructive 4 Chem 253, UC, Berkeley Observable diffraction peaks h2 k 2 l 2 Ratio SC: 1,2,3,4,5,6,8,9,10,11,12. -

An Asteroseismic Study of the Beta Cephei Star 12 Lacertae: Multisite
Mon. Not. R. Astron. Soc. 000, 1–15 (2002) Printed 31 October 2018 (MN LATEX style file v2.2) An asteroseismic study of the β Cephei star 12 Lacertae: multisite spectroscopic observations, mode identification and seismic modelling M. Desmet1⋆, M. Briquet1†, A. Thoul2‡, W. Zima1, P. De Cat3, G. Handler4, I. Ilyin5, E. Kambe6, J. Krzesinski7, H. Lehmann8, S. Masuda9, P. Mathias10, D. E. Mkrtichian11, J. Telting12, K. Uytterhoeven13, S. L. S. Yang14 and C. Aerts1,15 1 Institute of Astronomy - KULeuven, Celestijnenlaan 200D, 3001 Leuven, Belgium 2 Institut d’Astrophysique et de G´eophysique de l’Universit´ede Li`ege, 17, All´ee du 6 Aoˆut, 4000 Li`ege, Belgium 3 Koninklijke Sterrenwacht van Belgi¨e, Ringlaan 3, 1180 Brussel, Belgium 4 Institut f¨ur Astronomie, Universist¨at Wien, T¨urkenschanzstrasse 17, 1180 Wien, Austria 5 Astrophysical Institute Potsdam, An der Sternwarte 16 D-14482 Potsdam, Germany 6 Okayama Astrophysical Observatory, National Astronomical Observatory, Kamogata, Okayama 719-0232, Japan 7 Mt. Suhora Observatory, Cracow Pedagogical University, Ul. Podchorazych 2, 30-084 Cracow, Poland 8 Karl-Schwarzschild-Observatorium, Th¨uringer Landessternwarte, 7778 Tautenburg, Germany 9 Tokushima Science Museum, Asutamu Land Tokushima, 45 - 22 Kibigadani, Nato, Itano-cho, Itano-gun, Tokushima 779-0111, Japan 10 UNS, CNRS, OCA, Campus Valrose, UMR 6525 H. Fizeau, F-06108 Nice Cedex 2, France 11 Astronomical Observatory of Odessa National University, Marazlievskaya, 1v, 65014 Odessa, Ukraine 12 Nordic Optical Telescope, Apartado 474, 38700 Santa Cruz de La Palma, Spain 13 Instituto de Astrof´ısica de Canarias, Calle Via L´actea s/n, 38205 La Laguna (TF, Spain) 14 Department of Physics and Astronomy, Universtity of Victoria, Victoria, BC V8W 3P6, Canada 15 Department of Astrophysics, University of Nijmegen, PO Box 9010, 6500 GL Nijmegen, The Netherlands Accepted 2008. -

Diffraction-Free Beams in Fractional Schrödinger Equation Yiqi Zhang1, Hua Zhong1, Milivoj R
www.nature.com/scientificreports OPEN Diffraction-free beams in fractional Schrödinger equation Yiqi Zhang1, Hua Zhong1, Milivoj R. Belić2, Noor Ahmed1, Yanpeng Zhang1 & Min Xiao3,4 We investigate the propagation of one-dimensional and two-dimensional (1D, 2D) Gaussian beams in Received: 14 December 2015 the fractional Schrödinger equation (FSE) without a potential, analytically and numerically. Without Accepted: 11 March 2016 chirp, a 1D Gaussian beam splits into two nondiffracting Gaussian beams during propagation, while a 2D Published: 21 April 2016 Gaussian beam undergoes conical diffraction. When a Gaussian beam carries linear chirp, the 1D beam deflects along the trajectoriesz = ±2(x − x0), which are independent of the chirp. In the case of 2D Gaussian beam, the propagation is also deflected, but the trajectories align along the diffraction cone z =+2 xy22 and the direction is determined by the chirp. Both 1D and 2D Gaussian beams are diffractionless and display uniform propagation. The nondiffracting property discovered in this model applies to other beams as well. Based on the nondiffracting and splitting properties, we introduce the Talbot effect of diffractionless beams in FSE. Fractional effects, such as fractional quantum Hall effect1, fractional Talbot effect2, fractional Josephson effect3 and other effects coming from the fractional Schrödinger equation (FSE)4, introduce seminal phenomena in and open new areas of physics. FSE, developed by Laskin5–7, is a generalization of the Schrödinger equation (SE) that contains fractional Laplacian instead of the usual one, which describes the behavior of particles with fractional spin8. This generalization produces nonlocal features in the wave function. In the last decade, research on FSE was very intensive9–17. -

The Doubling of the Degrees of Freedom in Quantum Dissipative Systems, and the Semantic Information Notion and Measure in Biosemiotics †
Proceedings The Doubling of the Degrees of Freedom in Quantum Dissipative Systems, and the Semantic † Information Notion and Measure in Biosemiotics Gianfranco Basti 1,*, Antonio Capolupo 2,3 and GiuseppeVitiello 2 1 Faculty of Philosophy, Pontifical Lateran University, 00120 Vatican City, Italy 2 Department of Physics “E:R. Caianiello”, University of Salerno, Via Giovanni Paolo II, 132, 84084 Fisciano (SA), Italy; [email protected] (A.C.); [email protected] (G.V.) 3 Istituto Nazionale di Fisica Nucleare (INFN), Gruppo Collegato di Salerno, Via Giovanni Paolo II, 132, 84084 Fisciano (SA), Italy * Correspondence: [email protected]; Tel.: +39-339-576-0314 † Conference Theoretical Information Studies (TIS), Berkeley, CA, USA, 2–6 June 2019. Published: 11 May 2020 Keywords: semantic information; non-equilibrium thermodynamics; quantum field theory 1. The Semantic Information Issue and Non-Equilibrium Thermodynamics In the recent history of the effort for defining a suitable notion and measure of semantic information, starting points are: the “syntactic” notion and measure of information H of Claude Shannon in the mathematical theory of communications (MTC) [1]; and the “semantic” notion and measure of information content or informativeness of Rudolph Carnap and Yehoshua Bar-Hillel [2], based on Carnap’s theory of intensional modal logic [3]. The relationship between H and the notion and measure of entropy S in Gibbs’ statistical mechanics (SM) and then in Boltzmann’s thermodynamics is a classical one, because they share the same mathematical form. We emphasize that Shannon’s information measure is the information associated to an event in quantum mechanics (QM) [4]. Indeed, in the classical limit, i.e., whenever the classical notion of probability applies, S is equivalent to the QM definition of entropy given by John Von Neumann. -

Chapter 14 Interference and Diffraction
Chapter 14 Interference and Diffraction 14.1 Superposition of Waves.................................................................................... 14-2 14.2 Young’s Double-Slit Experiment ..................................................................... 14-4 Example 14.1: Double-Slit Experiment................................................................ 14-7 14.3 Intensity Distribution ........................................................................................ 14-8 Example 14.2: Intensity of Three-Slit Interference ............................................ 14-11 14.4 Diffraction....................................................................................................... 14-13 14.5 Single-Slit Diffraction..................................................................................... 14-13 Example 14.3: Single-Slit Diffraction ................................................................ 14-15 14.6 Intensity of Single-Slit Diffraction ................................................................. 14-16 14.7 Intensity of Double-Slit Diffraction Patterns.................................................. 14-19 14.8 Diffraction Grating ......................................................................................... 14-20 14.9 Summary......................................................................................................... 14-22 14.10 Appendix: Computing the Total Electric Field............................................. 14-23 14.11 Solved Problems .......................................................................................... -

Asteroseismology of the Β Cep Star HD 129929
A&A 415, 241–249 (2004) Astronomy DOI: 10.1051/0004-6361:20034142 & c ESO 2004 Astrophysics Asteroseismology of the β Cep star HD 129929 I. Observations, oscillation frequencies and stellar parameters C. Aerts1, C. Waelkens1, J. Daszy´nska-Daszkiewicz1,3,, M.-A. Dupret2,4,, A. Thoul2,†, R. Scuflaire2, K. Uytterhoeven1, E. Niemczura3, and A. Noels2 1 Instituut voor Sterrenkunde, Katholieke Universiteit Leuven, Celestijnenlaan 200 B, 3001 Leuven, Belgium 2 Institut d’Astrophysique et de G´eophysique, Universit´edeLi`ege, all´ee du Six Aoˆut 17, 4000 Li`ege, Belgium 3 Astronomical Institute of the Wrocław University, ul. Kopernika 11, 51-622 Wrocław, Poland 4 Instituto de Astrof´ısica de Andaluc´ıa-CSIC, Apartado 3004, 18080 Granada, Spain Received 1 August 2003 / Accepted 25 September 2003 Abstract. We have gathered and analysed a timeseries of 1493 high-quality multicolour Geneva photometric data of the B3V β Cep star HD 129929. The dataset has a time base of 21.2 years. The occurrence of a beating phenomenon is evident from the data. We find evidence for the presence of at least six frequencies, among which we see components of two frequency multiplets with an average spacing of ∼0.0121 c d−1 which points towards very slow rotation. This result is in agreement with new spectroscopic data of the star and also with previously taken UV spectra. We provide the amplitudes of the six frequencies in all seven photometric filters. The metal content of the star is Z = 0.018 ± 0.004. All these observational results will be used to perform detailed seismic modelling of this massive star in a subsequent paper. -

Index to JRASC Volumes 61-90 (PDF)
THE ROYAL ASTRONOMICAL SOCIETY OF CANADA GENERAL INDEX to the JOURNAL 1967–1996 Volumes 61 to 90 inclusive (including the NATIONAL NEWSLETTER, NATIONAL NEWSLETTER/BULLETIN, and BULLETIN) Compiled by Beverly Miskolczi and David Turner* * Editor of the Journal 1994–2000 Layout and Production by David Lane Published by and Copyright 2002 by The Royal Astronomical Society of Canada 136 Dupont Street Toronto, Ontario, M5R 1V2 Canada www.rasc.ca — [email protected] Table of Contents Preface ....................................................................................2 Volume Number Reference ...................................................3 Subject Index Reference ........................................................4 Subject Index ..........................................................................7 Author Index ..................................................................... 121 Abstracts of Papers Presented at Annual Meetings of the National Committee for Canada of the I.A.U. (1967–1970) and Canadian Astronomical Society (1971–1996) .......................................................................168 Abstracts of Papers Presented at the Annual General Assembly of the Royal Astronomical Society of Canada (1969–1996) ...........................................................207 JRASC Index (1967-1996) Page 1 PREFACE The last cumulative Index to the Journal, published in 1971, was compiled by Ruth J. Northcott and assembled for publication by Helen Sawyer Hogg. It included all articles published in the Journal during the interval 1932–1966, Volumes 26–60. In the intervening years the Journal has undergone a variety of changes. In 1970 the National Newsletter was published along with the Journal, being bound with the regular pages of the Journal. In 1978 the National Newsletter was physically separated but still included with the Journal, and in 1989 it became simply the Newsletter/Bulletin and in 1991 the Bulletin. That continued until the eventual merger of the two publications into the new Journal in 1997.