DOCSLIB.ORG

Classical and Modern Diffraction Theory

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Classical and Modern Diffraction Theory Downloaded from http://pubs.geoscienceworld.org/books/book/chapter-pdf/3701993/frontmatter.pdf by guest on 29 September 2021 Classical and Modern Diffraction Theory Edited by Kamill Klem-Musatov Henning C. Hoeber Tijmen Jan Moser Michael A. Pelissier SEG Geophysics Reprint Series No. 29 Sergey Fomel, managing editor Evgeny Landa, volume editor Downloaded from http://pubs.geoscienceworld.org/books/book/chapter-pdf/3701993/frontmatter.pdf by guest on 29 September 2021 Society of Exploration Geophysicists 8801 S. Yale, Ste. 500 Tulsa, OK 74137-3575 U.S.A. # 2016 by Society of Exploration Geophysicists All rights reserved. This book or parts hereof may not be reproduced in any form without permission in writing from the publisher. Published 2016 Printed in the United States of America ISBN 978-1-931830-00-6 (Series) ISBN 978-1-56080-322-5 (Volume) Library of Congress Control Number: 2015951229 Downloaded from http://pubs.geoscienceworld.org/books/book/chapter-pdf/3701993/frontmatter.pdf by guest on 29 September 2021 Dedication We dedicate this volume to the memory Dr. Kamill Klem-Musatov. In reading this volume, you will find that the history of diffraction We worked with Kamill over a period of several years to compile theory was filled with many controversies and feuds as new theories this volume. This volume was virtually ready for publication when came to displace or revise previous ones. Kamill Klem-Musatov’s Kamill passed away. He is greatly missed. new theory also met opposition; he paid a great personal price in Kamill’s role in Classical and Modern Diffraction Theory goes putting forth his theory for the seismic diffraction forward problem. far beyond that of co-editor. He was a pioneer of the extension of To model diffractions in the subsurface, he extended the diffraction modern diffraction theory of edge and tip waves to the seismic theory to take semi-transparent edges into account. For a number of method. His formulation of the seismic diffraction forward and years, this approach, a departure from the theory based on non-trans- inverse problems brought a new discipline to geophysics, one we parent edges, met strong opposition and criticism. might call the seismic diffraction method. In many ways, the Working with Kamill was a great honor and privilege for us. In purpose of Classical and Modern Diffraction Theory is to communi- remembering Kamill, a quote from Newton comes to mind “If I cate the theoretical foundations and their historical context to the geo- have seen further, it is by standing on the shoulders of giants.” physical community, for it is upon this foundation that Kamill based the seismic diffraction method. H. Hoeber, T. J. Moser, M. Pelissier Downloaded from http://pubs.geoscienceworld.org/books/book/chapter-pdf/3701993/frontmatter.pdf by guest on 29 September 2021 This page has been intentionally left blank Downloaded from http://pubs.geoscienceworld.org/books/book/chapter-pdf/3701993/frontmatter.pdf by guest on 29 September 2021 Table of Contents About the Editors ......................................................................................... vii Preface .................................................................................................... ix Acknowledgments .......................................................................................... xi Chapter 1: Overview . 1 The Fresnel diffraction phenomena ........................................................................ 3 W. Arkadiew The geometrical theory of diffraction ..................................................................... 13 J. B. Keller Diffraction theory ........................................................................................ 17 C. J. Bouwkamp Developments in our concepts of diffraction phenomena (on the 130th anniversary of the death of Thomas Young) ................................................................................... 57 G. D. Malyuzhinets Rays, waves and asymptotics ............................................................................. 67 J. B. Keller Rubinowicz and the modern theory of diffracted rays .................................................... 81 P. Ya. Ufimtsev Chapter 2: Early Developments in Diffraction Theory . 89 Translation editor’s introduction ........................................................................ 107 K. Helbig A physico-mathematical treatise on light, colors and the rainbow, Proposition 1 ........................... 108 F. M. Grimaldi Treatise on light, Chapter 1: On the rectilinear propagation of rays ...................................... 117 C. Huygens The Bakerian lecture: Experiments and calculations relative to physical optics ............................ 123 T. Young Chapter 3: The Classical Mathematical Theory of Diffraction . 129 Memoir on the diffraction of light ....................................................................... 147 A. Fresnel An essay on the application of mathematical analysis to the theories of electricity and magnetism ........................................................................... 177 G. Green Theory of air vibration in pipes with open ends .......................................................... 187 H. Helmholtz Downloaded from http://pubs.geoscienceworld.org/books/book/chapter-pdf/3701993/frontmatter.pdf by guest on 29 September 2021 vi Classical and Modern Diffraction Theory On the ray theory of light ............................................................................... 191 G. Kirchhoff On the passage of waves through apertures in plane screens, and allied problems ......................... 205 Lord Rayleigh (J. W. Strutt) Chapter 4: Foundations of Modern Diffraction Theory . 213 Reciprocal diffraction relations between circular and elliptical plates ..................................... 217 J. Coulson and G. G. Becknell An extension of the principle of the diffraction evolute, and some of its structural detail ................... 223 G. G. Becknell and J. Coulson An asymptotic treatment of diffraction problems ......................................................... 227 N. G. Van Kampen Boundary layer problems in diffraction theory ........................................................... 235 R. N. Buchal and J. B. Keller Geometrical theory of diffraction ........................................................................ 251 J. B. Keller A uniform geometrical theory of diffraction for an edge in a perfectly conducting surface ................. 267 R. G. Kouyoumjian and P. H. Pathak The ray method and the theory of edge waves ............................................................ 283 K. D. Klem-Musatov and A. M. Aizenberg Resolution and super-resolution in inverse diffraction ................................................... 293 M. Bertero, P. Boccacci, and M. Piana Appendix A: The Cornu Spiral ........................................................................ 303 New method for the discussion of diffraction problems in the case of a cylindrical wave ............... 305 M. A. Cornu Appendix B: Babinet’s Principle ....................................................................... 315 Memoirs on meteorological optics ................................................................... 317 M. Babinet The London and Edinburgh Philosophical Magazine and Journal of Science .......................... 319 A. Necker References: Reprinted Technical Papers ................................................................. 323 References: General ..................................................................................... 325 Downloaded from http://pubs.geoscienceworld.org/books/book/chapter-pdf/3701993/frontmatter.pdf by guest on 29 September 2021 About the Editors After the defense of his candidate dissertation on mathemat- ical physics (Ph.D. equivalent), Kamill joined the Institute of Pet- roleum Geology and Geophysics (Novosibirsk Scientific Centre, Siberian Branch, Russian Academy of Sciences, Russian Federa- tion) in 1968 and worked there for 47 academic years, until his last working day. For the first 12 academic years, Kamill’s scientific interests were devoted to a 2D canonical forward problem: wave diffraction in a sec- torial acoustic/elastic medium with one common sharp edge and several plane interfaces. He was one of the first scientists who obtained a rigorous solution of the difficult forward problem using the Sommer- feld-Malyuzhinets technique improved by him to semitransparent interfaces. He published a series of articles on this topic in Russian scientific journals. Among them, three results were the most valuable. The first of these is a justification of the edge-diffraction law: “amplitude of acoustic, elastic, electromagnetic and other edge Kamill D. Klem-Musatov, 1930–2015 waves inside the boundary layer (vicinity of shadow boundary) can be described by the universal special function W(w).” The second “All unknown and complex is hidden in the well-known and simple.” result is verification of this law by physical (laboratory) modeling. Using the above two results, Kamill and his pupil Evgeny Landa — Kamill D. Klem-Musatov introduced a theoretical criterion of detecting small-throw faults. Kamill summarized this period in his first monograph, Theory of On the morning of 18 June 2015, Professor Kamill D. Klem-Musatov, Edge Waves and its Application in Seismic (1980, in Russian). In doctor of science in mathematical physics, passed away at the age of 1980, he defended his doctoral dissertation based on the monograph 85
Load more

Recommended publications
  • What the Renaissance Knew Piero Scaruffi Copyright 2018
    What the Renaissance knew Piero Scaruffi Copyright 2018 http://www.scaruffi.com/know 1 What the Renaissance knew • The 17th Century – For tens of thousands of years, humans had the same view of the universe and of the Earth. – Then the 17th century dramatically changed the history of humankind by changing the way we look at the universe and ourselves. – This happened in a Europe that was apparently imploding politically and militarily, amid massive, pervasive and endless warfare – Grayling refers to "the flowering of genius“: Galileo, Pascal, Kepler, Newton, Cervantes, Shakespeare, Donne, Milton, Racine, Moliere, Descartes, Spinoza, Leibniz, Locke, Rubens, El Greco, Rembrandt, Vermeer… – Knowledge spread, ideas circulated more freely than people could travel 2 What the Renaissance knew • Collapse of classical dogmas – Aristotelian logic vs Rene Descartes' "Discourse on the Method" (1637) – Galean medicine vs Vesalius' anatomy (1543), Harvey's blood circulation (1628), and Rene Descartes' "Treatise of Man" (1632) – Ptolemaic cosmology vs Copernicus (1530) and Galileo (1632) – Aquinas' synthesis of Aristotle and the Bible vs Thomas Hobbes' synthesis of mechanics (1651) and Pierre Gassendi's synthesis of Epicurean atomism and anatomy (1655) – Papal unity: the Thirty Years War (1618-48) shows endless conflict within Christiandom 3 What the Renaissance knew • Decline of – Feudalism – Chivalry – Holy Roman Empire – Papal Monarchy – City-state – Guilds – Scholastic philosophy – Collectivism (Church, guild, commune) – Gothic architecture 4 What
    [Show full text]
  • Selected Correspondence of Descartes
    Selected Correspondence of Descartes René Descartes Copyright © Jonathan Bennett 2017. All rights reserved [Brackets] enclose editorial explanations. Small ·dots· enclose material that has been added, but can be read as though it were part of the original text. Occasional •bullets, and also indenting of passages that are not quotations, are meant as aids to grasping the structure of a sentence or a thought. Every four-point ellipsis . indicates the omission of a brief passage that has no philosophical interest, or that seems to present more difficulty than it is worth. (Where a letter opens with civilities and/or remarks about the postal system, the omission of this material is not marked by ellipses.) Longer omissions are reported between brackets in normal-sized type. —The letters between Descartes and Princess Elisabeth of Bohemia, omitted here, are presented elsewhere on this website (but see note on page 181).—This version is greatly indebted to CSMK [see Glossary] both for a good English translation to work from and for many explanatory notes, though most come from AT [see Glossary].—Descartes usually refers to others by title (‘M.’ for ‘Monsieur’ or ‘Abbé’ or ‘Reverend Father’ etc.); the present version omits most of these.—Although the material is selected mainly for its bearing on Descartes as a philosopher, glimpses are given of the colour and flavour of other sides of his life. First launched: April 2013 Correspondence René Descartes Contents Letters written in 1619–1637 1 to Beeckman, 26.iii.1619........................................................1
    [Show full text]
  • Intensity of Double-Slit Pattern • Three Or More Slits
    • Intensity of double-slit pattern • Three or more slits Practice: Chapter 37, problems 13, 14, 17, 19, 21 Screen at ∞ θ d Path difference Δr = d sin θ zero intensity at d sinθ = (m ± ½ ) λ, m = 0, ± 1, ± 2, … max. intensity at d sinθ = m λ, m = 0, ± 1, ± 2, … 1 Questions: -what is the intensity of the double-slit pattern at an arbitrary position? -What about three slits? four? five? Find the intensity of the double-slit interference pattern as a function of position on the screen. Two waves: E1 = E0 sin(ωt) E2 = E0 sin(ωt + φ) where φ =2π (d sin θ )/λ , and θ gives the position. Steps: Find resultant amplitude, ER ; then intensities obey where I0 is the intensity of each individual wave. 2 Trigonometry: sin a + sin b = 2 cos [(a-b)/2] sin [(a+b)/2] E1 + E2 = E0 [sin(ωt) + sin(ωt + φ)] = 2 E0 cos (φ / 2) cos (ωt + φ / 2)] Resultant amplitude ER = 2 E0 cos (φ / 2) Resultant intensity, (a function of position θ on the screen) I position - fringes are wide, with fuzzy edges - equally spaced (in sin θ) - equal brightness (but we have ignored diffraction) 3 With only one slit open, the intensity in the centre of the screen is 100 W/m 2. With both (identical) slits open together, the intensity at locations of constructive interference will be a) zero b) 100 W/m2 c) 200 W/m2 d) 400 W/m2 How does this compare with shining two laser pointers on the same spot? θ θ sin d = d Δr1 d θ sin d = 2d θ Δr2 sin = 3d Δr3 Total, 4 The total field is where φ = 2π (d sinθ )/λ •When d sinθ = 0, λ , 2λ, ..
    [Show full text]
  • Light and Matter Diffraction from the Unified Viewpoint of Feynman's
    European J of Physics Education Volume 8 Issue 2 1309-7202 Arlego & Fanaro Light and Matter Diffraction from the Unified Viewpoint of Feynman’s Sum of All Paths Marcelo Arlego* Maria de los Angeles Fanaro** Universidad Nacional del Centro de la Provincia de Buenos Aires CONICET, Argentine *[email protected] **[email protected] (Received: 05.04.2018, Accepted: 22.05.2017) Abstract In this work, we present a pedagogical strategy to describe the diffraction phenomenon based on a didactic adaptation of the Feynman’s path integrals method, which uses only high school mathematics. The advantage of our approach is that it allows to describe the diffraction in a fully quantum context, where superposition and probabilistic aspects emerge naturally. Our method is based on a time-independent formulation, which allows modelling the phenomenon in geometric terms and trajectories in real space, which is an advantage from the didactic point of view. A distinctive aspect of our work is the description of the series of transformations and didactic transpositions of the fundamental equations that give rise to a common quantum framework for light and matter. This is something that is usually masked by the common use, and that to our knowledge has not been emphasized enough in a unified way. Finally, the role of the superposition of non-classical paths and their didactic potential are briefly mentioned. Keywords: quantum mechanics, light and matter diffraction, Feynman’s Sum of all Paths, high education INTRODUCTION This work promotes the teaching of quantum mechanics at the basic level of secondary school, where the students have not the necessary mathematics to deal with canonical models that uses Schrodinger equation.
    [Show full text]
  • Image-Space Caustics and Curvatures
    Image-space Caustics and Curvatures Xuan Yu Feng Li Jingyi Yu Department of Computer and Information Sciences University of Delaware Newark, DE 19716, USA fxuan,feng,[email protected] Abstract Caustics are important visual phenomena, as well as challenging global illumination effects in computer graph- ics. Physically caustics can be interpreted from one of two perspectives: in terms of photons gathered on scene geom- etry, or in terms of a pair of caustic surfaces. These caustic surfaces are swept by the foci of light rays. In this paper, we develop a novel algorithm to approximate caustic sur- faces of sampled rays. Our approach locally parameterizes rays by their intersections with a pair of parallel planes. We show neighboring ray triplets are constrained to pass simul- taneously through two slits, which rule the caustic surfaces. We derive a ray characteristic equation to compute the two slits, and hence, the caustic surfaces. Using the characteris- tic equation, we develop a GPU-based algorithm to render the caustics. Our approach produces sharp and clear caus- tics using much fewer ray samples than the photon mapping method and it also maintains high spatial and temporal co- herency. Finally, we present a normal-ray surface repre- Figure 1. We use our caustic-surface-based sentation that locally parameterizes the normals about a algorithm to render the refraction caustics surface point as rays. Computing the normal ray caustic cast by a crystal bunny of 69473 triangles. On surfaces leads to a novel real-time discrete shape operator. an NVidia GeForce7800, our method renders at 115 fps at an image resolution of 512x512.
    [Show full text]
  • Caustic Architecture Article
    Tricks'of'the'light' An#extended#version#of#an#article#in#New$Scientist,#30#January#2013# # Two#men#enter#the#darkened#stage,#apparently#carrying#a#thick#slab#of#badly# made#glass,#like#the#stuff#in#the#windows#of#old#houses#that#turns#the#world# outside#wobbly.#They#hold#it#up,#and#computer#scientist#Mark#Pauly#shines#a# torch#at#it.#The#crowd#in#this#Parisian#auditorium#gasps#and#then#breaks#into# spontaneous#applause.# For#there#on#the#screen#behind,#conjured#out#of#this#piece#of#nearFfeatureless# material#–#not#glass,#in#fact,#but#transparent#acrylic#plastic#(Perspex)#–#is#a# projected#image#of#Alan#Turing,#the#computer#pioneer#whose#centenary#is# celebrated#this#year.#Every#thread#of#his#thick#tweed#jacket#is#picked#out#in#light# and#shadow.#But#where#is#the#image#coming#from?#It#can#only#be#the#transparent# slab,#but#there#seems#to#be#nothing#there#to#produce#it,#nothing#but#a#slightly# uneven#surface.# # An#image#of#Alan#Turing#conjured#from#light#passing#through#a#slab#of#Perspex#at#the# Advances#in#Architectural#Geometry#conference#in#Paris,#September#2012.# This#image#is#made#from#rays#refracted,#folded#and#focused#by#the#slightly# uneven#surface#of#the#acrylic#block.#It’s#similar#to#the#filigree#of#bright#bands#seen# on#the#bottom#of#a#swimming#pool#in#the#sunlight,#called#a#caustic#and#caused#by# the#way#the#wavy#surface#refracts#and#focuses#light.#Caustics#are#familiar#enough,# but#they#never#looked#like#this#before.#Those#made#by#sunlight#shining#through# an#empty#glass#are#a#random#mass#of#cusps#and#squiggles.#Pauly,#a#specialist#in#
    [Show full text]
  • Descartes' Optics
    Descartes’ Optics Jeffrey K. McDonough Descartes’ work on optics spanned his entire career and represents a fascinating area of inquiry. His interest in the study of light is already on display in an intriguing study of refraction from his early notebook, known as the Cogitationes privatae, dating from 1619 to 1621 (AT X 242-3). Optics figures centrally in Descartes’ The World, or Treatise on Light, written between 1629 and 1633, as well as, of course, in his Dioptrics published in 1637. It also, however, plays important roles in the three essays published together with the Dioptrics, namely, the Discourse on Method, the Geometry, and the Meteorology, and many of Descartes’ conclusions concerning light from these earlier works persist with little substantive modification into the Principles of Philosophy published in 1644. In what follows, we will look in a brief and general way at Descartes’ understanding of light, his derivations of the two central laws of geometrical optics, and a sampling of the optical phenomena he sought to explain. We will conclude by noting a few of the many ways in which Descartes’ efforts in optics prompted – both through agreement and dissent – further developments in the history of optics. Descartes was a famously systematic philosopher and his thinking about optics is deeply enmeshed with his more general mechanistic physics and cosmology. In the sixth chapter of The Treatise on Light, he asks his readers to imagine a new world “very easy to know, but nevertheless similar to ours” consisting of an indefinite space filled everywhere with “real, perfectly solid” matter, divisible “into as many parts and shapes as we can imagine” (AT XI ix; G 21, fn 40) (AT XI 33-34; G 22-23).
    [Show full text]
  • Real-Time Caustics
    EUROGRAPHICS 2003 / P. Brunet and D. Fellner Volume 22 (2003), Number 3 (Guest Editors) Real-Time Caustics M. Wand and W. Straßer WSI/GRIS, University of Tübingen Abstract We present a new algorithm to render caustics. The algorithm discretizes the specular surfaces into sample points. Each of the sample points is treated as a pinhole camera that projects an image of the incoming light onto the diffuse receiver surfaces. Anti-aliasing is performed by considering the local surface curvature at the sample points to filter the projected images. The algorithm can be implemented using programmable texture mapping hardware. It allows to render caustics in fully dynamic scenes in real-time on current PC hardware. Categories and Subject Descriptors: I.3.3 [Computer Graphics]: Picture / Image Generation – Display Algo- rithms; I.3.7 [Computer Graphics]: Three-Dimensional Graphics and Realism 1. Introduction tion step has to be performed that is often even more ex- pensive. Thus, the technique is usually not very efficient. A real-time simulation of the interaction of light with Although the implementation techniques for raytracing complex, dynamically changing scenery is still one of the queries have made impressive advances in the last few major challenges in computer graphics. In this paper, we years29, raytracing based algorithms still need a consider- look at a special global illumination problem, rendering of able amount of computational power (such as a cluster of caustics. Caustics occur if light is reflected (or refracted) at several high end CPUs) to calculate global illumination one or more specular surfaces, focused into ray bundles of solutions in real time30.
    [Show full text]
  • The Path Integral Approach to Quantum Mechanics Lecture Notes for Quantum Mechanics IV
    The Path Integral approach to Quantum Mechanics Lecture Notes for Quantum Mechanics IV Riccardo Rattazzi May 25, 2009 2 Contents 1 The path integral formalism 5 1.1 Introducingthepathintegrals. 5 1.1.1 Thedoubleslitexperiment . 5 1.1.2 An intuitive approach to the path integral formalism . .. 6 1.1.3 Thepathintegralformulation. 8 1.1.4 From the Schr¨oedinger approach to the path integral . .. 12 1.2 Thepropertiesofthepathintegrals . 14 1.2.1 Pathintegralsandstateevolution . 14 1.2.2 The path integral computation for a free particle . 17 1.3 Pathintegralsasdeterminants . 19 1.3.1 Gaussianintegrals . 19 1.3.2 GaussianPathIntegrals . 20 1.3.3 O(ℏ) corrections to Gaussian approximation . 22 1.3.4 Quadratic lagrangians and the harmonic oscillator . .. 23 1.4 Operatormatrixelements . 27 1.4.1 Thetime-orderedproductofoperators . 27 2 Functional and Euclidean methods 31 2.1 Functionalmethod .......................... 31 2.2 EuclideanPathIntegral . 32 2.2.1 Statisticalmechanics. 34 2.3 Perturbationtheory . .. .. .. .. .. .. .. .. .. .. 35 2.3.1 Euclidean n-pointcorrelators . 35 2.3.2 Thermal n-pointcorrelators. 36 2.3.3 Euclidean correlators by functional derivatives . ... 38 0 0 2.3.4 Computing KE[J] and Z [J] ................ 39 2.3.5 Free n-pointcorrelators . 41 2.3.6 The anharmonic oscillator and Feynman diagrams . 43 3 The semiclassical approximation 49 3.1 Thesemiclassicalpropagator . 50 3.1.1 VanVleck-Pauli-Morette formula . 54 3.1.2 MathematicalAppendix1 . 56 3.1.3 MathematicalAppendix2 . 56 3.2 Thefixedenergypropagator. 57 3.2.1 General properties of the fixed energy propagator . 57 3.2.2 Semiclassical computation of K(E)............. 61 3.2.3 Two applications: reflection and tunneling through a barrier 64 3 4 CONTENTS 3.2.4 On the phase of the prefactor of K(xf ,tf ; xi,ti) ....
    [Show full text]
  • Adaptive Spectral Mapping for Real-Time Dispersive Refraction By
    Adaptive Spectral Mapping for Real-Time Dispersive Refraction by Damon Blanchette A Thesis Submitted to the Faculty of the WORCESTER POLYTECHNIC INSTITUTE In partial fulfillment of the requirements for the Degree of Master of Science in Computer Science by ___________________________________ January 2012 APPROVED: ___________________________________ Professor Emmanuel Agu, Thesis Adviser ___________________________________ Professor Matthew Ward, Thesis Reader ___________________________________ Professor Craig Wills, Head of Department Abstract Spectral rendering, or the synthesis of images by taking into account the wavelengths of light, allows effects otherwise impossible with other methods. One of these effects is dispersion, the phenomenon that creates a rainbow when white light shines through a prism. Spectral rendering has previously remained in the realm of off-line rendering (with a few exceptions) due to the extensive computation required to keep track of individual light wavelengths. Caustics, the focusing and de-focusing of light through a refractive medium, can be interpreted as a special case of dispersion where all the wavelengths travel together. This thesis extends Adaptive Caustic Mapping, a previously proposed caustics mapping algorithm, to handle spectral dispersion. Because ACM can display caustics in real-time, it is quite amenable to be extended to handle the more general case of dispersion. A method is presented that runs in screen-space and is fast enough to display plausible dispersion phenomena in real-time at interactive frame rates. i Acknowledgments I would like to thank my adviser, Professor Emmanuel Agu, for his guidance, laughs, and answering my hundreds of questions over the year it took to complete this thesis. The beautiful video card helped, too.
    [Show full text]
  • Simple Cubic Lattice
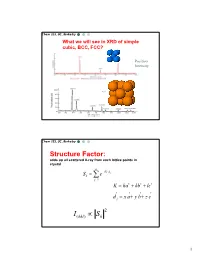
    Chem 253, UC, Berkeley What we will see in XRD of simple cubic, BCC, FCC? Position Intensity Chem 253, UC, Berkeley Structure Factor: adds up all scattered X-ray from each lattice points in crystal n iKd j Sk e j1 K ha kb lc d j x a y b z c 2 I(hkl) Sk 1 Chem 253, UC, Berkeley X-ray scattered from each primitive cell interfere constructively when: eiKR 1 2d sin n For n-atom basis: sum up the X-ray scattered from the whole basis Chem 253, UC, Berkeley ' k d k d di R j ' K k k Phase difference: K (di d j ) The amplitude of the two rays differ: eiK(di d j ) 2 Chem 253, UC, Berkeley The amplitude of the rays scattered at d1, d2, d3…. are in the ratios : eiKd j The net ray scattered by the entire cell: n iKd j Sk e j1 2 I(hkl) Sk Chem 253, UC, Berkeley For simple cubic: (0,0,0) iK0 Sk e 1 3 Chem 253, UC, Berkeley For BCC: (0,0,0), (1/2, ½, ½)…. Two point basis 1 2 iK ( x y z ) iKd j iK0 2 Sk e e e j1 1 ei (hk l) 1 (1)hkl S=2, when h+k+l even S=0, when h+k+l odd, systematical absence Chem 253, UC, Berkeley For BCC: (0,0,0), (1/2, ½, ½)…. Two point basis S=2, when h+k+l even S=0, when h+k+l odd, systematical absence (100): destructive (200): constructive 4 Chem 253, UC, Berkeley Observable diffraction peaks h2 k 2 l 2 Ratio SC: 1,2,3,4,5,6,8,9,10,11,12.
    [Show full text]
  • Advanced Computer Graphics CS 563: Adaptive Caustic Maps Using Deferred Shading
    Advanced Computer Graphics CS 563: Adaptive Caustic Maps Using Deferred Shading Frederik Clinckemaillie Computer Science Dept. Worcester Polytechnic Institute (WPI) ItIntrod ucti on: CtiCaustics Reflective Caustics Refractive Caustics IdiIntroduction: CiCaustic MiMapping Much faster than path tracing algorithms Two‐pass process Similar to photon mapping Creates a caustic intensity map CtiCaustic MiMapping Three Step Process 1) Photon Emission 2) Rearrangement into Caustic Map 3) Caustic Map Projection CtiCaustic MiMapping Phot on EiiEmission Rasterizes from light view to generate grid of photons Creates photon buffer 2D image storing final photon hit points In conjunction with shadow maps Allows quick lookups to determine Indirect lighting from caustics CtiCaustic Map CtiCreation Controls lighting quality and cost Splatting photons into caustic map becomes bo ttlenec k Crisp noise‐free images require millions of phthotons Not feasible in interactive time Hierarchical caustic maps: discard unimportant parts of photon buffer to improve speed Uses multi‐resolution caustic map to reduce splatting costs Problems Poor photon sampling due to rasterization leads to under and over sampling Proper sampling resolution cannot be determined Millions of photons are required for high‐quality caustics. Processing each is too expensive Photon sampling location can change between frames, leading to coherency problems Photon sampling is not dynamic DfDeferre d Shadi ng Good sampling rates cannot be computed Ideally, number of photons is determined adtildaptively Hierarchical Caustic Map(HCM) Has a maximum number of photons, not all are processed Pho ton EiiEmission and CtiCaustic Map GtiGeneration should be coupled DfDeferre d Shadi ng Postpones final illumination computations until visible fragments are identified HCMs generates grid of phthotons and only processes relevant ones DfDeferre d Sha ding never generates ilirrelevan t photons.
    [Show full text]