DOCSLIB.ORG

Exploring Different Probability Distributions for Rainfall Data of Kodagu - an Assisting Approach for Food Security

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Exploring Different Probability Distributions for Rainfall Data of Kodagu - an Assisting Approach for Food Security Int.J.Curr.Microbiol.App.Sci (2020) 9(2): 2972-2980 International Journal of Current Microbiology and Applied Sciences ISSN: 2319-7706 Volume 9 Number 2 (2020) Journal homepage: http://www.ijcmas.com Original Research Article https://doi.org/10.20546/ijcmas.2020.902.339 Exploring Different Probability Distributions for Rainfall Data of Kodagu - An Assisting Approach for Food Security R. Shreyas1*, D. Punith1, L. Bhagirathi2, Anantha Krishna3 and G. M. Devagiri4 1UAHS (Shivamogga), College of Forestry,Ponnampet, Karnataka-571216, India 2Department of Basic Sciences, College of Forestry, Ponnampet, Karnataka-571216, India 3Department of Computer Science, College of Forestry, Ponnampet, Karnataka-571216, India 4Department of Natural Resource Management, College of Forestry, Ponnampet, Karnataka-571216, India *Corresponding author ABSTRACT Rainfall intensity, duration and its distribution play a major role in the growth of agriculture and other related sectors and the overall development of a country. The present study is carried out to know the best fitting K e yw or ds probability distribution for rainfall data in three different taluks of Kodagu Rainfall, probability District. The time series data of average monthly and annual rainfall over a distributions, fitting, period of 61 years (1958-2018) was collected from KSNDMC, Bangalore. goodness-of-fit Around 26 different probability distributions were used to evaluate the best Article Info fit for annual and seasonal rainfall data. Kolmogorov-Smirnov, Anderson Darling and Chi-squared tests were used for the goodness of fit test. The Accepted: 20 January 2020 best fitting distribution was identified by maximum score which is a sum of Available Online: ranks given by three selected goodness of fit test for the distributions which 10 February 2020 is again based on fitting distance. Among various distributions attempted- Log Logistic (3P), Dagum, Gamma (3P), Inverse Gaussian, Generalized Gamma, Pearson Type 5 (3P) and Pearson 6 were found to be the best fit for annual and seasonal rainfall for different taluks of Kodagu district. Introduction amount of rainfall during the monsoon season is very important for economic activity. Indian agriculture sector accounts for around 14 percent of the country’s economy but Rainfall intensity, duration and its distribution accounts for 42 percent of total employment play a major role in the growth of agriculture in the country. About 55 percent of India’s and other related sectors and the overall arable land depends on precipitation, the development of a country. Rainfall intensity, 2972 Int.J.Curr.Microbiol.App.Sci (2020) 9(2): 2972-2980 patterns and its distribution are altered by medicine, climatology, economics and natural climatic variability i.e., decadal agricultural science. Probability distributions changes in circulation (Deepthi K.A, 2015) as of rainfall have been studied by many well as human induced changes i.e., land use researchers. and cover, emission of greenhouse gases, etc. The variability in rainfall affects the The main objective of this study is to identify agricultural production, water supply, a suitable probability distribution for annual transportation, the entire economy of a region, and seasonal rainfall in the different taluks of and the existence of its people. In regions Kodagu. where the year-to-year variability is high, people often suffer great calamities due to Materials and Methods floods or droughts. The damage due to extremes of rainfall cannot be avoided Kodagu district with an area of 4102 km sq. is completely, a forewarning could certainly be one of the smallest districts in the state of useful and it’s possible from analysis of Karnataka, located between 11056’00’’ and rainfall data. 12050’00’’ North latitude and between 75022’00” and 76011’00” East longitude. The In India, the monsoon or rainy season is average annual rainfall is around 2682 mm dominated by the humid South West (Anonymous, 2018). The District is composed Monsoon that sweeps across the country in of three taluks namely Madikeri, Somwarpet early June, first hitting the State of Kerala. and Virajpet. The southwest monsoon is generally expected to begin in early June and end by September Data and the total rainfall of these four months is considered as monsoon rainfall. In Indian Rainfall of three taluks of Kodagu district was agriculture, the contribution of south-west selected with annual and seasonal series from monsoon is immense as more than 70% of 1958 to 2018. The required rainfall data for India’s annual rainfall is from the south west the study was collected from Karnataka State monsoon and supports nearly 75% of the Natural Disaster Monitoring Centre kharif crop which is critical to India’s food (KSNDMC) situated at Bangalore. security. Methodology The prediction of rainfall at a particular place and time can be made by studying the The procedures adopted for this work can be behavior of rainfall of that place over several summarized in the following steps: years during the past. This behavior is best studied by fitting a suitable distribution to the Statistics of annual and seasonal period time series data on the rainfall (Kainth 1996). rainfall The rainfall is predicted with the help of the probability estimates. Probability and Using the sample data (i=1, 2…, n) the basic frequency analysis of rainfall data enables to statistical descriptors of the annual rainfall determine the expected rainfall at different series, the mean, standard deviation, probability level (Mishra et al., 2013). coefficient of variation (CV), skewness, kurtosis, minimum and maximum values, The probability distributions are used in have been estimated for each taluk of Kodagu different fields of science such as engineering, district. 2973 Int.J.Curr.Microbiol.App.Sci (2020) 9(2): 2972-2980 Distribution Fitting (0.05) level of significance for the selection of the best fit distribution. The hypothesis under The annual average and seasonal period the GOF test is: rainfall data for each of the 3 taluk of Kodagu district are fitted to the selected 26 continuous H0: MMR data follow the specified probability distributions as presented in table 1. distribution, H1: MMR data does not follow the specified Testing the goodness of fit distribution. The goodness-of-fit tests namely, The best fitted distribution is selected based Kolmogorov Smirnov test, Anderson-Darling on the minimum error produced, which is test and Chi-Squared test were used at α evaluated by the following techniques: Table.1 Description for continuous probability distribution Sl Distributio Probability Distribution Function f(x) Range/values Parameters No n 1 1 Burr (3P) x , , 0 ,as hape ak 0 x scale fx() 1 x 1 1 2 Burr (4P) x ,as hape ak x scale fx() 1 location xy 1 3 Dagum 1 ,as hape x (3P) ak scale 1 x 1 1 4 Dagum x ,as hape (4P) ak scale 1 location xy 1 5 Fatigue xx// 1 x , , 0 as hape Life . 0 x scale 2 (x y ) x 2974 Int.J.Curr.Microbiol.App.Sci (2020) 9(2): 2972-2980 6 Fatigue , , 0 as hape Life (3P) ()//()xx 1 x x scale . 2 (x y ) x location 7 Gamma ()x 1 , , 0 as hape (2P) f( x ) exp( x / ) () 0 x scale 8 Gamma ()x 1 , , 0 (3P) f( x ) exp( ( x ) / ) () x 9 1 Gen. 1 1 1 , , 0 exp( (1 zz ) )(1 ) 0 Extreme x fx( ) 1 Value exp(zz exp( )) 0 Gen. k 1 k, a s hape kx x k Gamma exp( ( ) ) scale 10 k () , , 0 11 Gen. kx() k 1 0 x f( x ) exp( (( x ) )k ) Gamma k () (4P) 12 Gumbel 1 x ,as scale hape f( x ) exp( z exp( z )) Max x locationscale Where, location x fx() 13 Inv. ()x 2 ,0 shape Gaussian 32exp 22xx 0 x location 14 2 shape Inv. ()x ,0 Gaussian exp 2 (xx )32 2 ( ) x , location (3P) 15 2 Johnson 1 z x , shape fx( ) exp ln SB 2zz (1 ) 21 z scale location 16 2 Log- 1 Logistic xx 1 2975 Int.J.Curr.Microbiol.App.Sci (2020) 9(2): 2972-2980 17 2 Log- 1 , , 0 as hape Logistic xx 1 x scale (3P) location , , 0 as hape 18 Log- 1 0 1 ln(XX ) ln( ) fx( ) exp 0 x scale Pearson 3 X () 0 , , 0 00xe y x exy 0 19 Log- 2 0 shape 1 ln(x Normal exp scale 2 0 x x2 20 Log- 2 0 shape 1 ln(x ) Normal exp scale (3P) 2 x (x ) 2 location 21 Pearson 5 exp( x ) ( )(x ) 1 22 Pearson 5 exp( (x )) (3P) 1 ( )((x ) ) 23 1 1 Pearson 6 ()x 12, , 0 12, shape fx() 12 scale Bx( 12 , )(1 ) 0 x 24 1 1 Pearson 6 ((x ) ) 12, , 0 12, shape fx() (4P) 12 scale Bx( 12 , )(1 ( ) ) x location 25 Weibull 1 xx fx( ) exp , , 0 26 Weibull 1 xx (3P) fx( ) exp 0 x 2976 Int.J.Curr.Microbiol.App.Sci (2020) 9(2): 2972-2980 Kolmogorov-Smirnov test Where Oiis the observed frequency for bin i, 2 and Eiis the expected (theoretical) x Is used to decide if a sample (x1, x2,xn ) with frequency for bin I calculated by Ei=F(X2) - CDF F(x) comes from a hypothesized F(X1), F is the CDF of the probability continuous distribution. The Kolmogorov- distribution being tested, X1 and X2 limits for Smirnov statistic (D) is based on the largest bin i. vertical difference between the theoretical CDF and the empirical (observed) CDF and is Based on Kolmogorov-Smirnov, Anderson- given by Darling and Chi-squared GOF test statistic ii1 values, 3 different rankings have been given Dmax F ( xii ) , F ( x ) to each of the distributions for all the taluk. 1innn No rank is given to a distribution when the concerned test fails to fit the data.
Load more

Recommended publications
  • Hampi, Badami & Around
    SCRIPT YOUR ADVENTURE in KARNATAKA WILDLIFE • WATERSPORTS • TREKS • ACTIVITIES This guide is researched and written by Supriya Sehgal 2 PLAN YOUR TRIP CONTENTS 3 Contents PLAN YOUR TRIP .................................................................. 4 Adventures in Karnataka ...........................................................6 Need to Know ........................................................................... 10 10 Top Experiences ...................................................................14 7 Days of Action .......................................................................20 BEST TRIPS ......................................................................... 22 Bengaluru, Ramanagara & Nandi Hills ...................................24 Detour: Bheemeshwari & Galibore Nature Camps ...............44 Chikkamagaluru .......................................................................46 Detour: River Tern Lodge .........................................................53 Kodagu (Coorg) .......................................................................54 Hampi, Badami & Around........................................................68 Coastal Karnataka .................................................................. 78 Detour: Agumbe .......................................................................86 Dandeli & Jog Falls ...................................................................90 Detour: Castle Rock .................................................................94 Bandipur & Nagarhole ...........................................................100
    [Show full text]
  • Kodagu District, Karnataka
    GOVERNMENT OF INDIA MINISTRY OF WATER RESOURCES CENTRAL GROUND WATER BOARD GROUND WATER INFORMATION BOOKLET KODAGU DISTRICT, KARNATAKA SOMVARPET KODAGU VIRAJPET SOUTH WESTERN REGION BANGALORE AUGUST 2007 FOREWORD Ground water contributes to about eighty percent of the drinking water requirements in the rural areas, fifty percent of the urban water requirements and more than fifty percent of the irrigation requirements of the nation. Central Ground Water Board has decided to bring out district level ground water information booklets highlighting the ground water scenario, its resource potential, quality aspects, recharge – discharge relationship, etc., for all the districts of the country. As part of this, Central Ground Water Board, South Western Region, Bangalore, is preparing such booklets for all the 27 districts of Karnataka state, of which six of the districts fall under farmers’ distress category. The Kodagu district Ground Water Information Booklet has been prepared based on the information available and data collected from various state and central government organisations by several hydro-scientists of Central Ground Water Board with utmost care and dedication. This booklet has been prepared by Shri M.A.Farooqi, Assistant Hydrogeologist, under the guidance of Dr. K.Md. Najeeb, Superintending Hydrogeologist, Central Ground Water Board, South Western Region, Bangalore. I take this opportunity to congratulate them for the diligent and careful compilation and observation in the form of this booklet, which will certainly serve as a guiding document for further work and help the planners, administrators, hydrogeologists and engineers to plan the water resources management in a better way in the district. Sd/- (T.M.HUNSE) Regional Director KODAGU DISTRICT AT A GLANCE Sl.No.
    [Show full text]
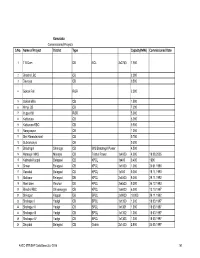
  • Karnataka Commissioned Projects S.No. Name of Project District Type Capacity(MW) Commissioned Date
    Karnataka Commissioned Projects S.No. Name of Project District Type Capacity(MW) Commissioned Date 1 T B Dam DB NCL 3x2750 7.950 2 Bhadra LBC CB 2.000 3 Devraya CB 0.500 4 Gokak Fall ROR 2.500 5 Gokak Mills CB 1.500 6 Himpi CB CB 7.200 7 Iruppu fall ROR 5.000 8 Kattepura CB 5.000 9 Kattepura RBC CB 0.500 10 Narayanpur CB 1.200 11 Shri Ramadevaral CB 0.750 12 Subramanya CB 0.500 13 Bhadragiri Shimoga CB M/S Bhadragiri Power 4.500 14 Hemagiri MHS Mandya CB Trishul Power 1x4000 4.000 19.08.2005 15 Kalmala-Koppal Belagavi CB KPCL 1x400 0.400 1990 16 Sirwar Belagavi CB KPCL 1x1000 1.000 24.01.1990 17 Ganekal Belagavi CB KPCL 1x350 0.350 19.11.1993 18 Mallapur Belagavi DB KPCL 2x4500 9.000 29.11.1992 19 Mani dam Raichur DB KPCL 2x4500 9.000 24.12.1993 20 Bhadra RBC Shivamogga CB KPCL 1x6000 6.000 13.10.1997 21 Shivapur Koppal DB BPCL 2x9000 18.000 29.11.1992 22 Shahapur I Yadgir CB BPCL 1x1300 1.300 18.03.1997 23 Shahapur II Yadgir CB BPCL 1x1301 1.300 18.03.1997 24 Shahapur III Yadgir CB BPCL 1x1302 1.300 18.03.1997 25 Shahapur IV Yadgir CB BPCL 1x1303 1.300 18.03.1997 26 Dhupdal Belagavi CB Gokak 2x1400 2.800 04.05.1997 AHEC-IITR/SHP Data Base/July 2016 141 S.No. Name of Project District Type Capacity(MW) Commissioned Date 27 Anwari Shivamogga CB Dandeli Steel 2x750 1.500 04.05.1997 28 Chunchankatte Mysore ROR Graphite India 2x9000 18.000 13.10.1997 Karnataka State 29 Elaneer ROR Council for Science and 1x200 0.200 01.01.2005 Technology 30 Attihalla Mandya CB Yuken 1x350 0.350 03.07.1998 31 Shiva Mandya CB Cauvery 1x3000 3.000 10.09.1998
    [Show full text]
  • Rating Rationale Brickwork Ratings Assigns “BWR-KA-D” (Provisional) for the Tourism – Homestay Rating of the Hillz Homestay, Madikeri, Kodagu District, Karnataka
    Rating Rationale Brickwork Ratings assigns “BWR-KA-D” (Provisional) for the Tourism – Homestay Rating of The Hillz Homestay, Madikeri, Kodagu District, Karnataka Brickwork Ratings India Pvt Ltd (BWR) has assigned “BWR-KA-D”#* (Provisional) (Pronounced BWR Karnataka D) Tourism – Homestay rating to The Hillz Homestay, Madikeri, Kodagu District, Karnataka which indicates that the organization provides/delivers Average Quality of Facility. This Provisional Rating is valid for 6 months and will be considered as a regular rating at the discretion of BWR, upon submission of the Original Homestay Registration Certificate issued by the Department of Tourism, Government of Karnataka. HOMESTAY PROFILE: The Hillz Homestay (THH), Madikeri, Kodagu District, Karnataka was established by Mrs. Beebijan and her family. THH is located at #76, Kudige Road, Kudumangalore Village and Post, Kushalnagar - Somwarpet Taluk, Kodagu District, Karnataka. THH is located around 3 Kms from Kushalnagar town and the approach road is motorable. The home stay is built on land area of ~10 cents and the built up area is ~ 6 cents. THH is a budget homestay and suitable for couples, groups and travelers. THH is a new homestay and operations are yet to start. It has 2 rooms on the first floor of the building to accommodate guests. THH is around 3 Kms from Kushalnagar town center, around 91 kms from Mysore and 170 Kms from Mangalore in Karnataka. OPERATIONS, FACILITIES AND SERVICES: The Hillz Homestay (THH) enjoys locational advantages, as it is situated in Madikeri with tourist attractions like Madikeri Fort which is around 2 kms from the home stay and Dubare which is 27 Km from the hometay .
    [Show full text]
  • Karnataka, India
    Natural Perception by Kodagu communities Georgina Zamora - Karnataka, India- UNIVERSITAT AUTÒNOMA DE BARCELONA Tutor Victoria Reyes-García, ICREA Ethnoecology Laboratory Georgina Zamora Quílez Degree on Environmental Sciences 1 Natural Perception by Kodagu communities Georgina Zamora Detailed Index Advertisement ............................................................................................................. 5 Acknowledgments ....................................................................................................... 6 I. INTRODUCTION........................................................................................................ 7 II. LITERATURE REVISION .......................................................................................... 8 1. Natural Capital Origins ............................................................................................. 8 2. Natural Goods and services....................................................................................... 9 2.1 Natural resources............................................................................................... 9 2.2 Ecosystem services ............................................................................................ 9 2.3 NNRR/Ecosystem services and sustainable development ..................................... 10 3 Natural Capital........................................................................................................ 11 3.1 Concept..........................................................................................................
    [Show full text]
  • Coffee Board Government of India Ministry of Commerce and Industry P.B
    Coffee Board, Head Office Coffee Board Government of India Ministry of Commerce and Industry P.B. No. 5366, Bengaluru - 560 001 Phone: 080- 22266991 - 994 Shri. M.S. Boje Gowda Chairman Phone No: Office:080-22200040 Fax: 080-22255557 Shri. Srivatsa Krishna, IAS Secretary Phone No. Off:080-22252917/ 22250250 Fax:080-22255557 Email:secretary[dot]coffeeboard[at]gmail[dot]com ........... Dr. Y. Raghuramulu Director of Finance Director of Research Phone No: Office: 22257690 Telefax:: Office: 080-22268700 Res: ........ Email: dr[dot]coffeeboard[at]nic[dot]in Email: dirfin[dot]coffeeboard[at]nic[d ot]in, dirfincb[at]gmail[dot]com Dr. K. Basavaraj Dr. D.R. Babu Reddy Head Division (Coffee Quality) Dy. Director (Market Research) Phone No: Office: 22262868 Phone No: Office: 22261584 Res: 23538256 Email: ddmr[dot]coffeeboard[at]nic[d Email: hdqc[dot]coffeeboard[at]nic[dot]in ot]in Dr.Tasveem Ahmed Shoeeb Shri. M.P. Damodaran Deputy Director (P & C) Deputy Director (Official Language) Phone No: Office: 22255266 Phone No: Office: 22266991-4 Telefax: 22268700 Mobile: 9448721076 Mobile: ......... Email:cbolwing[at]gmail[dot]com Email:ddpc[dot]coffeeboard[at]nic[dot]in ddol[dot]coffeeboard[at]nic[dot]in ............., Shri. ..................... Deputy Director (A/cs) Divisional Head (Engineering) Phone No: 22375921 Phone: 22342384 Mob: ............ Mob: ............. Email: [email protected]; Email: dhengg[dot]coffeeboard[at]nic ddaccts[dot]coffeeboard[at]nic[dot]in [dot]in Venkata Reddy Y.B Shri. Shivakumara Swamy B Senior Liaison Officer(Programme Senior Liaison Officer (Admin) Manager Unit) Phone No: Office: 22266991 Phone No: Office:.... Fax: 22255557 Mob: 8095722733 Email: osdadmncb[at]gmail[dot]com Email:......
    [Show full text]
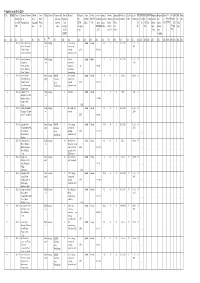
  • Kodagu Updated F-Register As on 31-03-2019
    F-Register as on 31-03-2019 Sl.No. PCBID Year of Name & Address Address Area/ Taluk District Name of the Type of Product Category Size Colour date of capital Present Applicabi Water Act Air Act Air Act HW HWM BM BMW Registrati Registrat Batte E- E- MS MS Rem Identifica of the of the Place/ Industrial Organisat No (L/M/S/ (R/O/G/ establish investme Working lity under (Validity) (Y/N) (Validity M (Validi W (Valid on under ion ry Waste Wast W W arks tion (YY- Organisations Organisat Ward Estates/ ion/ (XGN Micro) W) ment nt (in Status Water ) (Y/ ty) (Y/ ity) Plastic under (Y/N (Y/N) e (Y/ (Vali YY) ions No. areas Activity* category (DD/MM Lakhs) (O/C1/ Act N) N) rules plastic ) (Vali N) dity) (I/ M/ code) /YY) C2/Y)** (Y/N) (Y/N) rules dity) LB/HC/ (validity (8) H/L/CE/ date) (1) (2) (3) (4) (5) (6) (7) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) 1 2013-14 A.R. Coffee Curing Virajp Kodagu I Coffee curing, Small Green 13.65 O Y 31-12-2021 31-12- N Works, Halagunda et roasting and 2021 Village, Virajpet grinding 1572 30/11/1999 _ taluk, Coorg District. (industrial scale) 2 2013-14 Abrar Engineering Madik Kodagu I General Small White 3.5 O Y 31-12-2114 31-12- N Corporation, eri Engineering 2114 P.B.No.46, Plot Industries 14 25/9/2001 _ No.L4, Industrial (Excluding Estate, Madikeri, electroplating, 3 2013-14 Aimara Coffee Somw Kodagu KIADB I Coffee curing, Small Green 48 C1 Y Closed Closed N Curing Works, 1p, arpet Industrial roasting and Kiadb Industrial Area, grinding 1572 23/7/1999 _ Area, Kushalnagar, Kushalnagar (industrial scale) Virajpet taluk, 4 2013-14 Akshara Wood Virajp Kodagu I Saw mills Small Green 5 Y Y YTC YTC N Industries, No.89/11, et Mathoon Village, 11/7/2002 _ Virajpet taluk, Coorg.
    [Show full text]
  • Kodagu District Disaster Management Plan 2017-18
    Kodagu District Disaster Management Plan 2017-18 Kodagu District Disaster Management Plan 2017-18 Kodagu District map Message (Deputy Commissioner) Kodagu District Disaster Management Plan 2017-18 Index Content Page No. Abbreviation 1 Kodagu District Disaster Management Team 2-4 Chapter-1 INTRODUCTION 5-14 PART – A 1. DISTRICT PROFILE 1.1 Geography 1.2 Rainfall And Climate 1.3 Demography Of The Land 1.4 Kodagu District Administrative Setup 1.5 Socio Economic Profile Of The District 1.6.A. Agriculture 1.6.B. Geo Morphology Of Soil Types 1.6.C. Education 1.6.D. Tourism 1.6.E. Land Utilization Details 1.6.F. Infrastructure 1.6.G. Critical Infrastructures Of The District PART- B 15-18 1.7 Key Resources Of The Kodagu District 1.7a Details Of Rivers And Dams 1.7b Details Of Drinking Water 1.7c Flora And Fauna 1.8 Road Network 1.9 Details Of Media And Communications 1.10. Details of Power Generating Industries 1.11 Details Of Industries PART-C 19-26 1.12 Kodagu District Disaster Management Plan 1.12. A Scope Of The Kodagu District Disaster Management Plan: 1.12. B Kodagu - District Disaster Management Authority (DDMA):- 1.12.C. Laws And Statues 1.12.D Powers And Functions Of Kodagu District Authority 1.12.E The Plan development 1.13 Stake Holders And Their Responsibility 1.14 Kodagu ULBs And Their Support For Dm Plan 1.15. Formal Agreement (MOU) With Utility Agencies Kodagu District Disaster Management Plan 2017-18 1.16 How To Use The DDMP Plan 1.17 Approval Mechanism Of The DDMP – Authority For Implementation (State Level/District Level Orders)
    [Show full text]
  • JLR Began Decades Ago
    A R E N D E Z V O U S W I T H T H E W I L D JUNGLE LODGES & RESORTS A Government of Karnataka Undertaking, Karnataka, India PIONEERS IN ECO-TOURISM SINCE 1980 Sakrebyle Elephant Camp Dedicated to responsible and sustainable tourism, Aanejari Jungle Camp Jungle Lodges & Resorts is India's largest public sector River Tern Lodge company, aiding in efforts of wildlife conservation, Seethanadi Bhagawathi Jungle Camp Jungle Camp assisting enthusiasts in experiencing pristine nature and promoting livelihoods of communities living WILDLIFE CAMP TREKKING adjacent to the forest areas. It offers breathtaking BIRDWATCHING destinations, from isolated beaches to dense tropical SAFARI forests, from magnificent rivers to rugged hillsides in WATER BASED ADVENTURE ELEPHANT CAMP the beautiful wildlife reserves of Karnataka. HIGH ON ADVENTURE RELAXING BY THE BEACH KANNUR AIRPORT ONE STATE. MANY WORLDS. 2 JUNGLE LODGES & RESORTS JUNGLE LODGES & RESORTS 1 PIONEERS IN ECO-TOURISM SINCE 1980 Sakrebyle Elephant Camp Dedicated to responsible and sustainable tourism, Aanejari Jungle Camp Jungle Lodges & Resorts is India's largest public sector River Tern Lodge company, aiding in efforts of wildlife conservation, Seethanadi Bhagawathi Jungle Camp Jungle Camp assisting enthusiasts in experiencing pristine nature and promoting livelihoods of communities living WILDLIFE CAMP TREKKING adjacent to the forest areas. It offers breathtaking BIRDWATCHING destinations, from isolated beaches to dense tropical SAFARI forests, from magnificent rivers to rugged hillsides in WATER BASED
    [Show full text]
  • Sainik School Kodagu (Karnataka) (Ministry of Defence: Estd: 2007)
    SAINIK SCHOOL KODAGU (KARNATAKA) (MINISTRY OF DEFENCE: ESTD: 2007) PHONE: (08276) 278714 Sainik School Kodagu FAX : (08276) 278965 (Under Ministry of Defence) PO: Kudige Dist. Kodagu Email : [email protected] Karnataka- 571232 SSKG/QM/Woollen Blankets/2019 05 Sep 19 M/s ___________________________ ______________________________ REQUEST FOR PROPOSAL / INVITATION OF QUOTATION FOR SUPPLY OF WOOLLEN BLANKETS TO SAINIK SCHOOL KODAGU TWO BID SYSTEM Sir / Madam 1. On behalf of the Principal, Sainik School Kodagu the undersigned invites tender / quotations for “SUPPLY OF WOOLLEN BLANKETS” at Sainik School Kodagu. 2. The tender form addressed to your firm is attached to this letter. You may quote your minimal rates on the tender form and put your firms’ seal with signature on the same. Last date of receipt of duly filled in tender / quotation at this school is 15 Nov 19 (Fri) by 1500 hrs in person or by post in a sealed envelope on the mailing address as mentioned in the tender form duly marked on the top “SUPPLY OF WOOLLEN BLANKETS“ and underlined. Thanking you. Yours faithfully, Encl. As above SAINIK SCHOOL KODAGU (KARNATAKA) (MINISTRY OF DEFENCE: ESTD: 2007) PHONE: (08276) 278714 Sainik School Kodagu FAX : (08276) 278965 (Under Ministry of Defence) PO: Kudige Dist. Kodagu Email : [email protected] Karnataka- 571232 REQUEST FOR PROPSAL (RFP) Invitation of Bids for “SUPPLY OF WOOLLEN BLANKETS – TWO BID SYSTEM” Request for Proposal (RFP) No. SSKG/QM/Woollen Blankets dated 05 Sep 19. 1. Bids in sealed cover are invited for supply of items and execution of work as listed in part II RFP. Please super scribe the above mentioned Title, RFP number and date of opening of the bids on the sealed cover to avoid the bid being declared invalid.
    [Show full text]
  • Karnataka Bank Ltd
    Karnataka Bank Ltd. Your Family Bank, Across India. Phone : 0824-2427811 Asset Recovery Management Branch E-Mail : [email protected] III Floor, Karnataka Bank Building, Website : www.karnatakabank.com Kodialbail, Mangaluru – 575003 CIN : L85110KA1924PLC001128 PUBLIC NOTICE OF SALE Notice to the public is hereby given to the effect that the immovable property described herein below mortgaged to Kodlipet Branch has been taken Symbolic Possession thereof by the Authorised Officer on 11.06.2018 in pursuance of Section 13(4) of the Securitisation and Reconstruction of Financial Assets and Enforcement of Security Interest Act, 2002. The same will be sold by inviting tenders from the public on the date, place and time mentioned in this notice, on “as is where is condition” and on the terms and conditions mentioned below. Tenders in sealed covers are invited from the public for the purchase of the immovable property more fully described below. This Notice should be treated as Notice under sub-rule (6) of Rule (8) of the Security Interest Enforcement Rules 2002 to the Borrower and Co-obligant/ Guarantor [A] Name and Address of the Borrower & Co-obligant Guarantor: 1) Shri.Abbas C.B, S/o Bapu, Chikkakolathur, Dundalli, Shanivarasanthe Post-571235. Somwarpet Taluk. 2) Smt. Zoorabi C. A, W/o Abbas C. B., Chikkakolathur, Dundalli, Shanivarsanthe -571235. Somwarpet Taluk. [B] Name and address of the secured creditor: Karnataka Bank Ltd., Kodlipet Branch. [C]Details of Secured Debt: PSOD A/c No.4097000600014701 with balance of Rs.15,98,430.50 with further interest from 01.03.2018 plus costs and other charges .
    [Show full text]
  • 23Rd September 2015 9.30 AM to 11.30 AM
    State Level Expert Appraisal Committee (SEAC), Karnataka (Constituted by the MoEF, Government of India) No. KSEAC: MEETING: 2015 Dept. of Ecology and Environment, Karnataka Government Secretariat, Room No. 710, 7th Floor, I Stage, M.S. Building, Bangalore, Date:-18.09.2015 Additional Agenda for 148th Meeting of SEAC scheduled to be held on 21st, 22nd and 23rd September 2015 21st September 2015 9.30 AM to 11.30 AM EIA Presentation 148.140 Development of "Nadaprabhu Kempegowda Residential Layout" at Yeshwanthpura Hobli, Bangalore North Taluk and Kengeri Hobli, Bangalore South Taluk, Bangalore Urban District of Sri L. Raghu, Executive Enginner, Nadaprabhu Kempegowda Residential Layout (NKPL) Division, MRCP Layout, BDA Complex, Vijayanagar, Bangalore- 560040. (SEIAA 51 CON 2015) 4.00 PM to 5.30 PM 148.141 Building Stone Quarry Project, Sy.No.57/1 of Kakkihalli Village, Alur Taluk & Hassan Dist. (1-0 Acre) of Sri A H Abubakar S/o. Late Sri Aji Asainara, No.26-A, Jannapura- Kelagallale, Sakaleshpura Taluk, Hassan District. (SEIAA 833 MIN 2015) 148.142 Building Stone Quarry Project, Sy.No.29 of Huluvenahalli Village, Bengaluru South Taluk & Urban Dist. (9-20 Acres) of Sri P Thippeswamy (SEIAA 952 MIN 2015) 22nd September 2015 9.30 AM to 11.30 AM 148.143 Building Stone Quarry Project at Sy. No. 197/5 of Padaganur Village, Sindagi Taluk, Vijayapura District (1.3051 Ha) of M/s. Hi-Tech Rock Products & Aggregates Limited., (SEIAA 1086 MIN 2015) 148.144 Building Stone Quarry Project at Sy. No. 30/6 of Tawaregera Village, Kalburgi Taluk and District (2.6807 Ha) of M/s Hi-Tech Rock Products & Aggregates Limited., (SEIAA 1087 MIN 2015) 148.145 Building Stone Quarry Project at Sy.
    [Show full text]