194 on the Effect Produced on Mica, Gypsum, and Calcite, by The
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Mineralogy and Geology of the \Vkgnerite Occurrence Co Santa Fe Mountain, Front Range, Cobrado
Mineralogy and Geology of the \Vkgnerite Occurrence co Santa Fe Mountain, Front Range, Cobrado GEOLOGICAL SURVEY PROFESSIONAL PAPER 955 Mineralogy and Geology of the Wignerite Occurance on Santa Fe Mountain, Front Range, Colorado By DOUGLAS M. SHERIDAN, SHERMAN P. MARSH, MARY E. MROSE, and RICHARD B. TAYLOR GEOLOGICAL SURVEY PROFESSIONAL PAPER 955 A detailed mineralogic study of wagnerite, a rare phosphate mineral occurring in the report area in Precambrian gneiss; this is the first recorded occurrence of wagnerite in the United States UNITED STATES GOVERNMENT PRINTING OFFICE, WASHINGTON : 1976 UNITED STATES DEPARTMENT OF THE INTERIOR THOMAS S. KLEPPE, Secretary GEOLOGICAL SURVEY V. E. McKelvey, Director Library of Congress Cataloging in Publication Data Main entry under title: Mineralogy and geology of the wagnerite occurrence on Santa Fe Mountain, Front Range, Colorado. (Geological Survey Professional Paper 955) Includes bibliographical references. 1. Wagnerite Colorado Santa Fe Mountain. 2. Geology Colorado Santa Fe Mountain. I. Sheridan, Douglas M., 1921- II. Series: United States Geological Survey Professional Paper 955. QE391.W3M56 549'.72 76-10335 For sale by the Superintendent of Documents, U.S. Government Printing Office Washington, B.C. 20402 Stock Number 024-001-02844-1 CONTENTS Page Metric-English equivalents .............................. Descriptive mineralogy Continued Page Abstract............................................................ 1 Wagnerite............................................... 5 Introduction.................................................... -

By Sharon Francis Maxwell a Thesis Submitted in Partial
Essence [slide] by Sharon Francis Maxwell A thesis submitted in partial fulfillment of the requirements for the degree of Master of Fine Arts Montana State University © Copyright by Sharon Francis Maxwell (1993) Abstract: no abstract found in this volume ESSENCE by Sharon Francis Maxwell A thesis submitted in partial fulfillment of the requirements for the degree of Master of Fine Arts MONTANA STATE UNIVERSITY Bozeman, Montana April 1993 a / ^ (A 4 4 ° 1 ii APPROVAL of a thesis submitted by Sharon Francis Maxwell This thesis has been read by each member of the thesis committee and has been found to be satisfactory regarding content, English usage, format citations, bibliographic style, and consistency, and is ready for submission to the College of Graduate Studies. Approved for the Major Department , I icpartmerv Approved for the College of Graduate Studies Date Graduate Dean iii STATEMENT OF PERMISSION TO USE In presenting this thesis in partial fulfillment of the requirements for a master’s degree at Montana State University, I agree that the Library shall make it available to borrowers under rules of the Library. If I have indicated my intention to copyright this thesis by including a copyright notice page, copying is allowable only for scholarly purposes, consistent with "fair use" as prescribed in the US. Copyright Law. Requests for permission for extended quotation from or reproduction of this thesis in whole or in parts may be granted only by the copyright holder. Signatur Date I ARTIST’S STATEMENT Flowers have inspired mankind for thousands of years, providing a lasting and endless variety of motifs. -
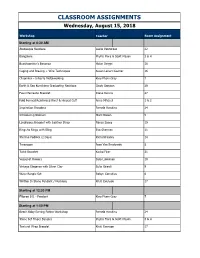
CLASSROOM ASSIGNMENTS Wednesday, August 15, 2018
CLASSROOM ASSIGNMENTS Wednesday, August 15, 2018 Workshop Teacher Room Assignment Starting at 8:30 AM Arabesque Necklace Leslie Venturoso 22 Bangalore Phyllis Flora & Scott Mason 3 & 4 Beachcomber's BonanzaHelen Driggs 18 Caging and Brazing + Wire TechniquesSusan Lenart Kazmer 16 Chroniker – Intro to MetalworkingKieu Pham Gray 7 Earth & Sea Kumihimo Graduating NecklaceCindy Grayson 29 Faux Marcasite Bracelet Diane Dennis 27 Fold Formed Reinforced Rivet & Hinged CuffAnne Mitchell 1 & 2 Inspiration Bracelets Pamela Hawkins 24 Introducing Niobium Marti Brown 5 Lavalicious Bracelet with Leather StrapNancy Sacco 19 Rings to Rings with BlingEva Sherman 11 Sterling Padlock (2 Days)Richard Salley 14 Treescape Jean Van Brederode 8 Twist Bracelet Kaska Firor 31 Vessel of Flowers Sara Lukkonen 10 Vintage Elegance with Silver ClaySulie Girardi 9 Wave Bangle Set Robyn Cornelius 6 Written In Stone Pendant / NecklaceKristi Evenson 17 Starting at 12:30 PM Filigree 101 - Pendant Kieu Pham Gray 7 Starting at 1:00 PM Beach Baby Earring Patina WorkshopPamela Hawkins 24 Stone Set Finger BanglesPhyllis Flora & Scott Mason 3 & 4 Textural Wrap Bracelet Kristi Evenson 17 CLASSROOM ASSIGNMENTS Thursday, August 16, 2018 Class Teacher Room Assignment Starting at 8:30 AM Art Nouveau Designs in Metal ClayLisel Crowley 32 Big Bling Ring Nancy Sacco 19 Chandelier Earrings Kaska Firor 31 Cold Connection Boot Camp: Rivets and Cold Joins for Jewelry Helen Driggs 18 and Mixed Media Discover Torch Enameling: Wild About WireSteven James 17 Eye of the Beholder Jean Van Brederode -

Phosphates, Arsenates, Vanadates, Antimonates A
592 DESCRIPTIVE MINERALOGY Epistdite. A niobate of uncertain composition. Analysis shows chiefly SjOz, TiOz, NkO, H20. Monoclinic. In rectangular plates, also in aggregates of curved foha. Basal cleavage perfect. H. = 1-1.5. G. = 2.9. Color white, grayish brownish. Refractive index 1.67. Bound in pegmatite veins or in massive albite from ~llianehaab,Greenland. Plumboniobite. A niobatc of yttrium, uranium, lead, iron, etc. Amorphous. H. = 5-5'5. G. = 4.81. Color dark brown to black. Found in mica mines at Morogoro, German Enst Africa. Oxygen Salts 4. PHOSPHATES, ARSENATES, VANADATES, ANTIMONATES A. Anhydrous Phosphates, Arsenates, Vanadates, Antimonates Normal phosphoric acid is H3P04, and consequently normal phosphates I 11 m have the formulas RtPOa, R3(PO4)2 and RPO4, and similarly for the arse- nates, etc. Only a comparatively small number of species conform to this simple formula. Most species contain more than one metallic element, and in the prominent Apatite Group the radical (CaF), (CaCI) or (PbCI) enters; " in the Wagnerite Group we have similarly (kF) or (ROH). XENOTIME. Tetragonal. Axis c = 0.6187, zz' (1 11 A ill) = 55" 301, 22" (111 A 771) = 82" 22'. In crystals resembling zircon in habit; sometimes compounded with zircon in parallel position (Fig. 462, p. 173). In 972 rolled grains. Cleavage: m (110) perfect. Fracture uneven and splintery. Brittle. H. = 4-5. G. = 4.454.56. Luster resinous to vitreous. Color yellowish brown, reddish brown, hair-brown, flesh-red, grayish white, wine-yellow, pale yellow; streak pale brown, yellow- ish or reddish. Opaque. Optically + . w = 1.72. e = 1-81. -

Book 700 Street Trees and Reticulation Design Version 1.2
Design and Construction Note Book 700 Street Trees and Reticulation Design Version 1.2 Book 700 - Amendments Version 1.0 29/06/2018 V1.0 Book 700 29/06/2018 Issued For Use Version 1.1 10/10/2018 V1.1 Book 700 17/10/2018 Backdrafted & Re-issued For Use Version 1.2 06/12/2018 V1.2 Book 700 06/12/2018 Backdrafted & Re-issued For Use Design and Construction Note 700.01 Street Trees and Reticulation Design Index Reviewed: 06/12/2018 Street Trees and Reticulation Design Index 700.00 Street Trees and Reticulation Design 700.00 Cover Page 700.01 Index Page 701.00 Reticulation Design 701.00 Reticulation Design - Sheet 1 701.01 Reticulation Design - Sheet 2 701.02 Reticulation Design - Sheet 3 701.03 Reticulation Design - Sheet 4 701.04 Reticulation Design - Sheet 5 701.05 Reticulation Design - Sheet 6 702.00 Tree-Pits and Tree-Grates 702.00 Standard Tree-Pit 702.01 Large Tree-Pit 702.02 Water Retention Tree-Pit in Granite Kerbs - Sheet 1 702.03 Water Retention Tree-Pit in Granite Kerbs - Sheet 2 702.04 Water Retention Tree-Pit in Concrete Kerbs - Sheet 1 702.05 Water Retention Tree-Pit in Concrete Kerbs - Sheet 2 702.06 Underground Structural Cells 702.07 Tree-Grate Frame - Installation - Sheet 1 702.08 Tree-Grate Frame - Installation - Sheet 2 702.09 Stainless Steel Tree-Grate 702.10 Stainless Steel Tree-Grate - Water Retention 702.11 Full Height Tree Guard 702.12 Soft installation of Trees 702.13 Water Harvesting Kerb Attachment Plate Details Book 700 - Issused For Use SHEET 1 of 1 This document has been prepared by The City of Perth and is subject to change. -

Oral History Interview with Carlyle H. Smith, 1994 August 8
Oral history interview with Carlyle H. Smith, 1994 August 8 Funding for the digital preservation of this interview was provided by a grant from the Save America's Treasures Program of the National Park Service. Contact Information Reference Department Archives of American Art Smithsonian Institution Washington. D.C. 20560 www.aaa.si.edu/askus Transcript Preface The following oral history transcript is the result of a recorded interview with Carlyle H. Smith on August 8, 1994. The interview took place in Boston, Massachusetts, and was conducted by Robert F. Brown for the Archives of American Art, Smithsonian Institution. This transcript has been lightly edited for readability by the Archives of American Art. The reader should bear in mind that they are reading a transcript of spoken, rather than written, prose. Interview ROBERT F. BROWN: Well, we're interviewing today, Carlyle H. Smith, and this is Robert Brown, the interviewer for the archives of American art, and we're interviewing at the archives' regional center in Boston, Massachusetts, on August 8, 1994. Now, you've said that you were born in 1912 in Torrington, Connecticut. You were born to a family that had been in that area for a very long time, is that right? CARLYLE H. SMITH: Yes. That'd been there since the early 1700s. And fact is, I think my dad was the first one of the family to ever leave the Torrington area. ROBERT F. BROWN: Now, Torrington was, what, a small manufacturing town? CARLYLE H. SMITH: It was a very busy manufacturing town at one time. -

Product Focus on Booksbooks
Cookson BIG Catalogue Product Focus on BooksBooks The widest choice of products, materials & equipment for the jewellery trade, all from one convenient source. ThereThere isis nothing like aa goodgood read...read... particularly if its about a subject which is new to you, or about which, you need to brush up on. Having a good book is important because it gives you the resource to troubleshoot and solve problems, it explains the hows and whys, and it puts you back on track when youve experimented with the tried and true. Learn a new skill or find comprehensive information and technical details that will help you perfect your technique! Jewellery: Fundametals of Handbook of Jewellery Metalsmithing Techniques By Tim McCreight NEW! By Carles Codina NEW! This introduction to basic techniques such as This book shows in step-by-step sequences, piercing, setting and soldering are explained how to accomplish various techniques with colour photographs. Also included are including enamelling, fusing, and soldering. examples of exciting work by a diverse range It also explains the pros and cons of of artists, a helpful glossary and valuable tables. Hardbound, 144 different materials and finishes and how to pages with 250 colour photographs. achieve them. Hardbound, 160 pages. Code No: 999 A19 £25.00 Code No: 999 A20 £20.00 Enamelling on Precious Metals Gemstones By Jeanne Werge-Hartley By Cally Hall NEW! NEW! Topics covered: An introduction to the Packed with detailed information on enamels and precious metals used for gemstone properties, varieties, chief enamelling. Details alternative approaches to characteristics and distinguishing champleve, cloisonne, and plique a jour. -

JMD Jewelry Soldering Basics How to Solder Jewelry: Solders, Flux, Tools
Jewelry Soldering Basics How to Solder Jewelry: Solders, Flux, Tools & Setup JEWELRY SOLDERING BASICS HOW TO SOLDER JEWELRY: SOLDERS, FLUX, TOOLS & SETUP SOLDER: WHAT IT IS, FLUX: HELP WHEN HOW TO USE IT SOLDER FLOWS 3 7 YOUR SOLDERING STATION: CREATE A PRACTICE PROJECT: FIRE-SAFE ZONE STACKING RING TRIO 11 17 BY LEXI ERICKSON SOMETIMES SOLDERING IS SIMPLER. Although learning how area in your workspace that is dedicated to soldering so you can to solder jewelry is a big step, it’s one that can save you time feel confident about working with hot metal, an open flame, and effort — even money. Connections that don’t involve silver and fuel for your torch. You’ll get a glossary of all the specialized solder or a torch might be easier to make in some cases, but for terms you’ll encounter about the basic jewelry soldering sup- some designs a solder join really makes the most sense. plies, tools, and pieces of equipment you’ll be using in your new soldering station. Soldering is the “gateway” jewelry making technique that will let you take your jewelry designs to a whole new level. Soldering lets And whether you've been soldering for a while or are just you do the seemingly impossible: take two pieces of metal and firing up your torch for the first time, you'll get step-by- create one single piece of metal with them. step instructions for a great little ring that makes the In this introductory eBook about soldering silver jewelry (copper, perfect soldering practice project: a silver band with too!), you’ll learn essential basic information you will use again one solder seam. -

Fine Chinese Works Of
AUCTION JUNE, 16TH 2018 Fine Chinese Works of Art 慵天ᷕ⚳喅埻⑩ and Buddhist Sculpturesġ ⍲ἃ㔁晽⁷ AUCTION Fine Chinese Works of Art FRONT COVER: Lot 120 – Detail A LARGE AND VERY RARE KANGXI 慵天ᷕ⚳喅埻⑩ PERIOD FAMILLE VERTE BALUSTER VASE ‘LIU HAI AND FEMALE IMMORTALS’ and Buddhist Sculptures BACK COVER: Lot 77 ⍲ἃ㔁晽⁷ A LARGE YUAN / MING DYNASTY PAINTING OF FEMALE DEITIES WITH th pm GESSO HIGHLIGHTS Saturday, June 16 2018 at 2 CET CATALOG CA0618 VIEWING www.zacke.at IN OUR GALLERY June 11th - June 16th Monday - Friday 10am - 6pm Saturday - June 16th 10am - 1pm and by appointment GALERIE ZACKE MARIAHILFERSTRASSE 112 Lot 98 A LARGE AND IMPORTANT MING 1070 VIENNA AUSTRIA DYNASTY POLYCHROME-LACQUERED WOOD FIGURE OF GUANYIN Tel +43 1 532 04 52 Fax +20 E-mail offi[email protected] 1 IMPORTANT INFORMATION ABSENTEE BIDDING FORM (According to the general terms and conditions of business Gallery Zacke Vienna) FOR THE AUCTION FINE CHINESE WORKS OF ART AND BUDDHIST SCULPTURES CATALOG CA0618 ON DATE Saturday, June 16th 2018 at 2pm CET NO. TITLE BID IN EURO Endangered Species / CITES Information Some items in this catalogue may consist of material such as for example ivory, rhinoceros horn, tortoise shell, coral or any rare types of tropical wood, and are therefore subject to the Convention on International Trade in Endangered Species of Wild Fauna and Flora [CITES]. Such items may only be exported outside the European Union after an export permit in accordance with CITES has been granted by the Austrian authorities. Zacke Gallery cannot and does not guarantee that such export permit may or will be obtained, but will by order of the winning bidder, once and exclusively after the item in question has been paid in full, apply to obtain such a permit at a fixed administrative fee of euro 500, - per application. -

Sintering and Mechanical Properties of Magnesium and Fluorine Co-Substituted Hydroxyapatites
Journal of Biomaterials and Nanobiotechnology, 2013, 4, 1-11 1 http://dx.doi.org/10.4236/jbnb.2013.41001 Published Online January 2013 (http://www.scirp.org/journal/jbnb) Sintering and Mechanical Properties of Magnesium and Fluorine Co-Substituted Hydroxyapatites Samia Nsar, Amel Hassine, Khaled Bouzouita* Laboratory of Industrial Chemistry, National School of Engineering, Sfax, Tunisia. Email: *[email protected] Received September 5th, 2012; revised October 17th, 2012; accepted November 10th, 2012 ABSTRACT Biological apatites contain several elements as traces. In this work, magnesium and fluorine co-substituted hydroxyapa- tites with the general formula Ca9Mg(PO4)6(OH)2-yFy, where y = 0, 0.5, 1, 1.5 and 2 were synthesized by the hydrother- mal method. After calcination at 500˚C, the samples were pressureless sintered between 950˚C and 1250˚C. The substi- tution of F− for OH− had a strong influence on the densification behavior and mechanical properties of the materials. Below 1200˚C, the density steeply decreased for y = 0.5 sample. XRD analysis revealed that compared to hydroxyl- fluorapatite containing no magnesium, the substituted hydroxyfluorapatites decomposed, and the nature of the decom- position products is tightly dependent on the fluorine content. The hardness, elastic modulus and fracture toughness of these materials were investigated by Vickers’s hardness testing. The highest values were 622 ± 4 GPa, 181 ± 1 GPa and 1.85 ± 0.06 MPa·m1/2, respectively. Keywords: Hydroxyapatite; Magnesium, Fluorine; Sintering; Mechanical Properties 1. Introduction tite containing magnesium and fluorine would be more suitable for dental and orthopedic applications. Hydroxyapatite (HA) is widely used in orthopedic and Hence, it is thought worthwhile to synthesize and char- reconstructive surgery thanks to its excellent bioactivity acterize Mg/F-co-substituted hydroxypatites. -

Diploma in Fine Jewellery Tools & Materials Kit List
Diploma in Fine Jewellery Tools & Materials Kit List 2021 Tool List As an intermediate jeweller it is expected that you will already have all of the standard silversmithing tools as set out on the Silver Jewellery Diploma tool list - which is why we don't offer a tool kit on this Diploma. Therefore below is a list of specific tools that you may need to purchase in addition to the ones you already have, and that you will need to have to hand for each project. Tools Required For All Projects Pendant motor and hammer hand-piece - This is the largest and most important tool that is additional for this course. A pendant motor is essential and a hammer hand-piece is highly recommended for the collet setting weeks. We have a detailed post on our blog on this https://www.jewellersacademy.com/blog/which-foredom-pendant-motor-should-i-buy-and- compatible-hammer-handpieces Soldering station complete with torch, fire bricks, flux, tweezers, flux brush, pickle Saw blades - a range of saw blade bundles in sizes 1/0 to 6/0 to use in different projects All the workshop basics needed for sawing, filing and polishing - saw frame, files, needle files etc. Riveting hammer 2 x dividers Your preferred polishing equipment - emery paper, sticks, 3M radial discs, rubber burrs, cotton mops, polishing cloths etc. Term 1 - Week 1: Reticulation & Keum Boo - Stud Earrings & Ring Making Hot plate Burnisher Honeycomb block (little section) for Keum Boo on earrings AA tweezers For cut outs for making Keum Boo - craft paper punch (optional) Scalpel or sharp scissors to -

Thermal Characterization of Magnesium Containing Ionomer Glasses
Thermal characterization of magnesium containing ionomer glasses ELENI MARIA KARTELIA Supervisor: Dr. A. Stamboulis Thesis submitted for the degree of MRes Biomaterials University of Birmingham School of Engineering Department of Metallurgy and Materials September, 2010 University of Birmingham Research Archive e-theses repository This unpublished thesis/dissertation is copyright of the author and/or third parties. The intellectual property rights of the author or third parties in respect of this work are as defined by The Copyright Designs and Patents Act 1988 or as modified by any successor legislation. Any use made of information contained in this thesis/dissertation must be in accordance with that legislation and must be properly acknowledged. Further distribution or reproduction in any format is prohibited without the permission of the copyright holder. ACKNOWLEDGMENTS I would like to thank my supervisor Dr. A. Stamboulis for her help and encouragement during my project. Without her support, I feel that I would not have been able to complete this work. I would also like to express my gratitude to Dr. D. Holland at University of Warwick for her helping on DSC measurements. Many thanks are given to academic staff and technicians of the School of Metallurgy and Materials. I would like to thank sincerely the Phd students Praveen Ramakrishnan, Georgina Kaklamani, Siqi Zhang and Mitra Kashani for their significant help through my experimental work. Last but not least, I would like to thank my family for their support and understanding. Special thanks to Thanos Papaioannou. 2 TABLE CAPTIONS CHAPTER 2: MATERIALS AND METHODS Table 2.1.2: Composition of Mg substituted alumino-silicate glasses.