Entropic Forces in Brownian Motion
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Inertial Mass of an Elementary Particle from the Holographic Scenario
Document downloaded from: http://hdl.handle.net/10459.1/62944 The final publication is available at: https://doi.org/10.1142/S0217751X17500439 Copyright (c) World Scientific Publishing, 2017 Inertial mass of an elementary particle from the holographic scenario Jaume Gin´e Departament de Matem`atica, Universitat de Lleida, Catalonia, Spain. E{mail: [email protected] Abstract Various attempts have been made to fully explain the mechanism by which a body has inertial mass. Recently it has been proposed that this mechanism is as follows: when an object accelerates in one direction a dy- namical Rindler event horizon forms in the opposite direction, suppressing Unruh radiation on that side by a Rindler-scale Casimir effect whereas the radiation in the other side is only slightly reduce by a Hubble-scale Casimir effect. This produces a net Unruh radiation pressure force that always op- poses the acceleration, just like inertia, although the masses predicted are twice those expected, see [17]. In a later work an error was corrected so that its prediction improves to within 26% of the Planck mass, see [10]. In this paper the expression of the inertial mass of a elementary particle is derived from the holographic scenario giving the exact value of the mass of a Planck particle when it is applied to a Planck particle. Keywords: inertial mass; Unruh radiation; holographic scenario, Dark matter, Dark energy, cosmology. PACS 98.80.-k - Cosmology PACS 04.62.+v - Quantum fields in curved spacetime PACS 06.30.Dr - Mass and density 1 Introduction The equivalence principle introduced by Einstein in 1907 assumes the com- plete local physical equivalence of a gravitational field and a corresponding non- inertial (accelerated) frame of reference (Einstein was thinking of his famous elevator experiment). -
![Quantization of Black Holes Is One of the Important Issues in Physics [1], and There Has Been No Satisfactory Solution Yet](https://docslib.b-cdn.net/cover/4093/quantization-of-black-holes-is-one-of-the-important-issues-in-physics-1-and-there-has-been-no-satisfactory-solution-yet-554093.webp)
Quantization of Black Holes Is One of the Important Issues in Physics [1], and There Has Been No Satisfactory Solution Yet
Quantization of Black Holes Xiao-Gang He1, 2, 3, 4, ∗ and Bo-Qiang Ma1, 2, 4, † 1School of Physics and State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing 100871 2Department of Physics and Center for Theoretical Sciences, National Taiwan University, Taipei 10617 3Institute of Particle Physics and Cosmology, Department of Physics, Shanghai JiaoTong University, Shanghai 200240 4Center for High-Energy Physics, Peking University, Beijing 100871 Abstract We show that black holes can be quantized in an intuitive and elegant way with results in agreement with conventional knowledge of black holes by using Bohr’s idea of quantizing the motion of an electron inside the atom in quantum mechanics. We find that properties of black holes can be also derived from an Ansatz of quantized entropy ∆S = 4πk∆R/λ, which was suggested in a previous work to unify the black hole entropy formula and Verlinde’s conjecture to explain gravity as an entropic force. Such an Ansatz also explains gravity as an entropic force from quantum effect. This suggests a way to unify gravity with quantum theory. Several interesting and surprising results of black holes are given from which we predict the existence of primordial black holes ranging from Planck scale both in size and energy to big ones in size but with low energy behaviors. PACS numbers: 04.70.Dy, 03.67.-a, 04.70.-s, 04.90.+e arXiv:1003.2510v3 [hep-th] 5 Apr 2010 ∗Electronic address: [email protected] †Electronic address: [email protected] 1 The quantization of black holes is one of the important issues in physics [1], and there has been no satisfactory solution yet. -

Statistical Mechanics of Entropic Forces: Disassembling a Toy
Home Search Collections Journals About Contact us My IOPscience Statistical mechanics of entropic forces: disassembling a toy This article has been downloaded from IOPscience. Please scroll down to see the full text article. 2010 Eur. J. Phys. 31 1353 (http://iopscience.iop.org/0143-0807/31/6/005) View the table of contents for this issue, or go to the journal homepage for more Download details: IP Address: 132.239.16.142 The article was downloaded on 06/12/2011 at 21:15 Please note that terms and conditions apply. IOP PUBLISHING EUROPEAN JOURNAL OF PHYSICS Eur. J. Phys. 31 (2010) 1353–1367 doi:10.1088/0143-0807/31/6/005 Statistical mechanics of entropic forces: disassembling a toy Igor M Sokolov Institut fur¨ Physik, Humboldt-Universitat¨ zu Berlin, Newtonstraße 15, D-12489 Berlin, Germany E-mail: [email protected] Received 21 June 2010, in final form 9 August 2010 Published 23 September 2010 Online at stacks.iop.org/EJP/31/1353 Abstract The notion of entropic forces often stays mysterious to students, especially to ones coming from outside physics. Although thermodynamics works perfectly in all cases when the notion of entropic force is used, no effort is typically made to explain the mechanical nature of the forces. In this paper we discuss the nature of entropic forces as conditional means of constraint forces in systems where interactions are taken into account as mechanical constraints and discuss several examples of such forces. We moreover demonstrate how these forces appear within the standard formalism of statistical thermodynamics and within the mechanical approach based on the Pope–Ching equation, making evident their connection with the equipartition of energy. -

Colloidal Matter: Packing, Geometry, and Entropy Vinothan N
Colloidal matter: packing, geometry, and entropy Vinothan N. Manoharan Harvard John A. Paulson School of Engineering and Applied Sciences and Department of Physics, Harvard University, Cambridge MA 02138 USA This is the author's version of the work. It is posted here by permission of the AAAS for personal use, not for redistribution. The definitive version was published in Science volume 349 on August 8, 2015. doi: 10.1126/science.1253751 The many dimensions of colloidal matter. The self-assembly of colloids can be controlled by changing the shape, topology, or patchiness of the particles, by introducing attractions between particles, or by constraining them to a curved surface. All of the assembly phenomena illustrated here can be understood from the interplay between entropy and geometrical constraints. Summary of this review article Background: Colloids consist of solid or liquid particles, each about a few hundred nanometers in size, dispersed in a fluid and kept suspended by thermal fluctuations. While natural colloids are the stuff of paint, milk, and glue, synthetic colloids with well-controlled size distributions and interactions are a model system for understanding phase transitions. These colloids can form crystals and other phases of matter seen in atomic and molecular systems, but because the particles are large enough to be seen under an optical microscope, the microscopic mechanisms of phase transitions can be directly observed. Furthermore, their ability to spontaneously form phases that are ordered on the scale of visible wavelengths makes colloids useful building blocks for optical materials such as photonic crystals. Because the interactions between particles can be altered and the effects on structure directly observed, experiments on colloids offer a controlled approach toward understanding and harnessing self-assembly, a fundamental topic in materials science, condensed matter physics, and biophysics. -

Nov/Dec 2020
CERNNovember/December 2020 cerncourier.com COURIERReporting on international high-energy physics WLCOMEE CERN Courier – digital edition ADVANCING Welcome to the digital edition of the November/December 2020 issue of CERN Courier. CAVITY Superconducting radio-frequency (SRF) cavities drive accelerators around the world, TECHNOLOGY transferring energy efficiently from high-power radio waves to beams of charged particles. Behind the march to higher SRF-cavity performance is the TESLA Technology Neutrinos for peace Collaboration (p35), which was established in 1990 to advance technology for a linear Feebly interacting particles electron–positron collider. Though the linear collider envisaged by TESLA is yet ALICE’s dark side to be built (p9), its cavity technology is already established at the European X-Ray Free-Electron Laser at DESY (a cavity string for which graces the cover of this edition) and is being applied at similar broad-user-base facilities in the US and China. Accelerator technology developed for fundamental physics also continues to impact the medical arena. Normal-conducting RF technology developed for the proposed Compact Linear Collider at CERN is now being applied to a first-of-a-kind “FLASH-therapy” facility that uses electrons to destroy deep-seated tumours (p7), while proton beams are being used for novel non-invasive treatments of cardiac arrhythmias (p49). Meanwhile, GANIL’s innovative new SPIRAL2 linac will advance a wide range of applications in nuclear physics (p39). Detector technology also continues to offer unpredictable benefits – a powerful example being the potential for detectors developed to search for sterile neutrinos to replace increasingly outmoded traditional approaches to nuclear nonproliferation (p30). -

Book of Abstracts Vol. II
Symposium A Advanced Materials: From Fundamentals to Applications INVITED LECTURES 1. Potassium hydroxide 2. Potassium hydride 3. Potassium carbonate 4. Sodium hydroxide 5. Sodium hydride 6. Sodium carbonate 7. Calcium hydroxide 8. Calcium carbonate 9. Calcium sulphate 10. Calcium nitrate 11. Calcium chloride 12. Barium hydroxide 13. Barium carbonate 14. Barium sulphate 15. Barium nitrate 16. Barium chloride 17. Aluminium sulphate 18. Aluminium nitrate 19. Aluminium chloride 20. Alum 21. Potassium silicate 22. Potassium silicate 23. Potassium calcium silicate 24. Potassium barium silicate 25. Silicon fluoride 26. Ammonium potassium 27. Ethylene chloride compound Chemical symbols used by Dalton, 19th century ← Previous page: Distilling apparatus from John French’s The art of distillation, London 1651 Symposium A: Advanced Materials A - IL 1 Binuclear Complexes as Tectons in Designing Supramolecular Solid-State Architectures Marius Andruh University of Bucharest, Faculty of Chemistry, Inorganic Chemistry Laboratory Str. Dumbrava Rosie nr. 23, 020464-Bucharest, Romania [email protected] We are currently developing a research project on the use of homo- and heterobinuclear complexes as building-blocks in designing both oligonuclear species and high-dimensionality coordination polymers with interesting magnetic properties. The building-blocks are stable binuclear complexes, where the metal ions are held together by compartmental ligands, or alkoxo- bridged copper(II) complexes. The binuclear nodes are connected through appropriate exo- - 3- III bidentate ligands, or through metal-containing anions (e. g. [Cr(NH3)2(NCS)4] , [M(CN)6] , M = Fe , CrIII). A rich variety of 3d-3d and 3d-4f heterometallic complexes, with interesting architectures and topologies of the spin carriers, has been obtained1. -

Holographic Theory, and Emergent Gravity As an Entropic Force
Holographic theory, and emergent gravity as an entropic force Liu Tao December 9, 2020 Abstract In this report, we are going to study the holographic principle, and the possibility of describing gravity as an entropic force, independent of the details of the microscopic dynamics. We will first study some of the deep connections between Gravity laws and thermodynamics, which motivate us to consider gravity as an entropic force. Lastly, we will investigate some theoretical criticisms and observational evidences on emergent gravity. 1 Contents 1 Introduction3 2 Black holes thermodynamics and the holographic principle3 2.1 Hawking temperature, entropy..........................3 2.1.1 Uniformly accelerated observer and the Unruh effect.........3 2.1.2 Hawking temperature and black hole entropy..............6 2.2 Holographic principle...............................7 3 Connection between gravity and thermodynamics8 3.1 Motivations (from ideal gas and GR near event horizon)...........8 3.2 Derive Einstein's law of gravity from the entropy formula and thermodynamics 10 3.2.1 the Raychaudhuri equation........................ 10 3.2.2 Einstein's equation from entropy formula and thermodynamics.... 11 4 Gravity as an entropic force 13 4.1 General philosophy................................ 13 4.2 Entropic force in general............................. 13 4.3 Newton's law of gravity as an entropic force.................. 14 4.4 Einstein's law of gravity as an entropic force.................. 15 4.5 New interpretations on inertia, acceleration and the equivalence principle.. 17 5 Theoretical and experimental criticism 18 5.1 Theoretical criticism............................... 18 5.2 Cosmological observations............................ 19 20section.6 2 1 Introduction The holographic principle was inspired by black hole thermodynamics, which conjectures that the maximal entropy in any region scales with the radius squared, and not cubed as might be expected for any extensive quantities. -

UC Riverside UC Riverside Electronic Theses and Dissertations
UC Riverside UC Riverside Electronic Theses and Dissertations Title A Hybrid Density Functional Theory for Solvation and Solvent-Mediated Interactions Permalink https://escholarship.org/uc/item/4p6713xb Author Jin, Zhehui Publication Date 2012 Peer reviewed|Thesis/dissertation eScholarship.org Powered by the California Digital Library University of California UNIVERSITY OF CALIFORNIA RIVERSIDE A Hybrid Density Functional Theory for Solvation and Solvent-Mediated Interactions A Dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Chemical and Environmental Engineering by Zhehui Jin March 2012 Dissertation Committee: Dr. Jianzhong Wu, Chairperson Dr. Ashok Mulchandani Dr. David Kisailus Copyright by Zhehui Jin 2012 The Dissertation of Zhehui Jin is approved: _________________________________________________ _________________________________________________ _________________________________________________ Committee Chairperson University of California, Riverside Acknowledgements This thesis is the result of five years of work whereby I have been accompanied and supported by many people. I would like to express the most profound appreciation to my advisor, Prof. Jianzhong Wu. He led me to the field of statistical thermodynamics and guided me to define research problems and solve these problems through theoretical approaches. I have been greatly benefited from his wide knowledge and logical way of thinking and gained fruitful achievements during my Ph.D. study. His enthusiasms on research and passion for providing high-quality research works have made a deep impression on me. I am deeply grateful to Dr. Yiping Tang, Prof. Zhengang Wang, Dr. De-en Jiang, Dr. Dong Meng, and Dr. Douglas Henderson who have assisted my research work and led me to different exciting fields of study. -

The Entropic Force in Reissoner-Nordström-De Sitter
Physics Letters B 797 (2019) 134798 Contents lists available at ScienceDirect Physics Letters B www.elsevier.com/locate/physletb The entropic force in Reissoner-Nordström-de Sitter spacetime ∗ Li-Chun Zhang a,b, Ren Zhao a,b, a Institute of Theoretical Physics, Shanxi Datong University, Datong 037009, China b Department of Physics, Shanxi Datong University, Datong 037009, China a r t i c l e i n f o a b s t r a c t Article history: We compare the entropic force between the black hole horizon and the cosmological horizon in Received 2 March 2019 Reissoner-Nordström-de Sitter (RN-dS) spacetime with the Lennard-Jones force between two particles. Received in revised form 21 July 2019 It is found that the former has an extraordinary similarity to the latter. We conclude that the black hole Accepted 22 July 2019 horizon and the cosmological horizon are not pure geometric surface, but have a definite “thickness”, Available online 24 July 2019 which is proportional to the radius of the horizons. In the case of no external force, according to different Editor: M. Cveticˇ initial condition, the relative position of the two horizons will experience first accelerated expansion, then decelerated expansion, or first accelerated contraction, then decelerated contraction. Therefore the whole Universe is oscillating. © 2019 The Authors. Published by Elsevier B.V. This is an open access article under the CC BY license (http://creativecommons.org/licenses/by/4.0/). Funded by SCOAP3. 1. Introduction nuity is of the first order; and the one with continuous entropy is of the second order. -

Liquid Crystalline Phases in Oligonucleotide Solutions
1TTWOW 0336.6 0SSVNV¥JVZ[P[\P[VKHSS\UPVULKLPZLN\LU[PLSLTLU[P 5LSSLWHNPULJOLZLN\VUVZVUVYPWVY[H[LSL]HYPHU[P KLSSVNVPUKP]PK\H[LWLYHKLN\HYZPJVUZ\JJLZZVHK S 3PTTHNPUL KLSSH 4PULY]H H YHWWYLZLU[HaPVUL 3H KLUVTPUHaPVUL <UP]LYZP[ KLNSP :[\KP KP VNUPLZPNLUaHKP\[PSPaaV0UWHY[PJVSHYL]LUNVUV KLSSH:HWPLUaHJVSSVJH[HZ\SSVZMVUKVKP\UWYVÉSV 4PSHUVYPWVY[H[HPUJHYH[[LYL[PWVNYHÉJV7HSH[PUV WYLZLU[H[LSL]HYPHU[PKPMVYTHYPN\HYKHU[PSHKP KLSSH JP[[ KP 4PSHUV YPJVUVZJPIPSL KH HSJ\UP KLP ;HSLLSLTLU[VJVZ[P[\PZJLWHY[LPU[LNYHU[LKLSSVNV ZWVZPaPVUL KLSSH 4PULY]H YPZWL[[V HSSH ZJYP[[H SL Z\VP LKPÉJP WP² JHYH[[LYPZ[PJP L JPYJVUKH[H KHSSH LUVUW\®WLYULZZ\UTV[P]V]LUPYLTVKPÉJH[V ]HYPHU[PKPJVSVYLLSL]HYPHU[PKPKPTLUZPVULLSH ZJYP[[H<UP]LYZP[HZ:[\KPVY\T4LKPVSHULUZPZ VKVTLZZV IVYH[LWLYV[[PTPaaHYLSHYLZHNYHÉJHKLSSVNVULSSH YPWYVK\aPVULZ\Z\WWVY[PKPKP]LYZVMVYTH[V Doctorate School in Physics, Astrophysics and Applied Physics LIQUID CRYSTALLINE PHASES IN OLIGONUCLEOTIDE SOLUTIONS FIS/03 Doctorate Thesis of: Giuliano ZANCHETTA XX cycle Advisor: Prof. Tommaso BELLINI Co-advisor: Dr. Guido TIANA Director of the school: Prof. Gianpaolo BELLINI Academic year 2006-2007 to Michi, artist of science, and to my women, Betta and Teresa "Le cose tutte quante hanno ordine tra loro, e questo `eforma che l'universo a Dio fa simigliante." (Dante, Paradiso, I, 103) [All things whate'er they be Have order among themselves, and this is form, That makes the universe resemble God] "Il pensiero pi`urisoluto, pi`uostinatamente perseguito, ´eniente in confronto a ci`oche avviene." (Cesare Pavese (1908-1950)) [The most determined, the most stubbornly pursued thought is nothing in comparison with what happens] Abstract In this thesis, we investigate the behavior of short complementary B-form DNA oligomers, 6 to 20 base pairs in length, exhibiting chiral nematic and colum- nar liquid crystal phases, even though such duplexes lack the shape anisotropy required for liquid crystal ordering. -

Protein Folding Proteins
Protein Folding Proteins: ● Proteins are biopolymers that form most of the cellular machinery ● The function of a protein depends on its 'fold' – its 3D structure Motor Chaperone Walker Levels of Folding: F T P A V L F A H D PRIMARY QUATERNARY K F L A S V T S V TERTIARY SECONDARY The Backbone ● Amino acids linked together R H O by peptide bonds 1 y y C 1 H a N 2 C' N f C' f C a N H 1 2 O R 2 Peptide Bond Steric constraints lead only to a subset of possible angles --> Ramachandran plot Glycine residues can adopt many angles a Helices 3.6 residues/turn b Sheets parallel sheet anti-parallel sheet other topologies possible but much more rare Classes of Folds: ● There are three broad classes of folds: a, b and a+b ● as of today, 103000 known structures --> 1100 folds (SCOP 1.75) alpha class beta class alpha+beta class myoglobin – stores oxygen TIM barrel – 10% of enzymes in muscle tissue streptavadin – used a lot adopt this fold, a great in biotech, binds biotin template for function Databases: SWISSPROT: contains sequence data of proteins – 100,000s of sequences Protein Data Bank (PDB): contains 3D structural data for proteins – 100,000 structures, x-ray & NMR SCOP: classifies all known structures into fold classes ~ 1100 folds Protein Folding: FOLDING amino acid sequence structure DESIGN ● naturally occurring sequences seem to have a unique 3D structure Levinthal paradox: if the polymer doesn't search all of conformation space, how on earth does it find its ground state, and in a reasonable time? if 2 conformation/residue & dt ~ 10-12 -> -
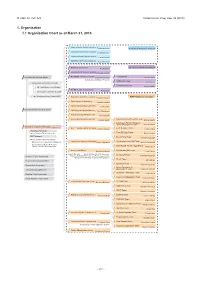
1. Organization 1.1 Organization Chart As of March 31, 2015
Ⅵ. RNC ACTIVITIES RIKEN Accel. Prog. Rep. 48 (2015) 1. Organization 1.1 Organization Chart as of March 31, 2015 Quantum Hadron Physics Laboratory Tetsuo Hatsuda Theoretical Research Division Theoretical Nuclear Physics Laboratory Takashi Nakatsukasa Strangeness Nuclear Physics Laboratory Emiko Hiyama Mathematical Physics Laboratory Koji Hashimoto Radiation Laboratory Sub Nuclear System Research Division Hideto En'yo Advanced Meson Science Laboratory Masahiko Iwasaki RIKEN BNL Research Center Theory Group President RIKEN Ryoji Noyori Samuel H. Aronson Larry McLerran Deputy Director:Robert Pisarski Computing Group Taku Izubuchi Nishina Center Advisory Council Experimental Group Yasuyuki Akiba RBRC Scientific Review Committee (SRC) Meeting RIKEN Facility Office at RAL Philip KING Advisory Committee for the RIKEN-RAL Muon Facility RBRC Management Steering Committee(MSC) Radioactive Isotope Physics Laboratory RIBF Research Division Hiroyoshi Sakurai Spin isospin Laboratory Tomohiro Uesaka Nuclear Spectroscopy Laboratory Hideki Ueno Nishina Center Planning Office High Energy Astrophysics Laboratory Toru Tamagawa Astro-Glaciology Research Unit Yuko Motizuki Research Group for Superheavy Element Superheavy Element Production Team Kosuke Morita Kosuke Morita Superheavy Element Research Device Development Team Kouji Morimoto Nishina Center for Accelerator-Based Science Hideto En'yo Nuclear Transmutation Data Research Group Fast RI Data Team Hiroyoshi Sakurai Hideakii Otsu Theoretical Research Slow RI Data Team Deputy Director:Tetsuo Hatsuda Koichi