A Uthor Abstra Ct
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Women's 3000M Steeplechase
Games of the XXXII Olympiad • Biographical Entry List • Women Women’s 3000m Steeplechase Entrants: 47 Event starts: August 1 Age (Days) Born SB PB 1003 GEGA Luiza ALB 32y 266d 1988 9:29.93 9:19.93 -19 NR Holder of all Albanian records from 800m to Marathon, plus the Steeplechase 5000 pb: 15:36.62 -19 (15:54.24 -21). 800 pb: 2:01.31 -14. 1500 pb: 4:02.63 -15. 3000 pb: 8:52.53i -17, 8:53.78 -16. 10,000 pb: 32:16.25 -21. Half Mar pb: 73:11 -17; Marathon pb: 2:35:34 -20 ht EIC 800 2011/2013; 1 Balkan 1500 2011/1500; 1 Balkan indoor 1500 2012/2013/2014/2016 & 3000 2018/2020; ht ECH 800/1500 2012; 2 WSG 1500 2013; sf WCH 1500 2013 (2015-ht); 6 WIC 1500 2014 (2016/2018-ht); 2 ECH 3000SC 2016 (2018-4); ht OLY 3000SC 2016; 5 EIC 1500 2017; 9 WCH 3000SC 2019. Coach-Taulant Stermasi Marathon (1): 1 Skopje 2020 In 2021: 1 Albanian winter 3000; 1 Albanian Cup 3000SC; 1 Albanian 3000/5000; 11 Doha Diamond 3000SC; 6 ECP 10,000; 1 ETCh 3rd League 3000SC; She was the Albanian flagbearer at the opening ceremony in Tokyo (along with weightlifter Briken Calja) 1025 CASETTA Belén ARG 26y 307d 1994 9:45.79 9:25.99 -17 Full name-Belén Adaluz Casetta South American record holder. 2017 World Championship finalist 5000 pb: 16:23.61 -16. 1500 pb: 4:19.21 -17. 10 World Youth 2011; ht WJC 2012; 1 Ibero-American 2016; ht OLY 2016; 1 South American 2017 (2013-6, 2015-3, 2019-2, 2021-3); 2 South American 5000 2017; 11 WCH 2017 (2019-ht); 3 WSG 2019 (2017-6); 3 Pan-Am Games 2019. -

INA Newsletter Vol 15 Part 2 1993 SALAMANCA ABSTRACTS
15/2 5th 1993 INTERNATIONAL NAN KTON ASSOCIATION VOLUME 15 UMBER 2 1993 ~&Rb~~ j CJ\ltl\ INTERNATIONAL NANNOPLANKTON \ ASSOCIATION 5th CONFERENCE SALAMANCA, SPAIN 30th August - 2nd September 1993 ABSTRACTS Conference Convenor Jose-Abel Flores Villarejo Organising Committee Francisco-Javier Sierro Jorge Civis Guillermo Prances Angeles Barcena Jose Angel Gonzalez Delgado Abstract volume edited by, J.R. Young & P.R. Bown INA Newsletter 15/1, 1993 - Salamanca Abstracts 41 EDITORS NOTES AND ACKNOWLEDGEMENTS The abstracts are not exactly as submitted since this volume was mainly produced via a Kurzweil text scanner - which converted the heterogeneous original copy into word processor files. The accuracy of scanning is dependant on the print quality of the originals and despite checking it is inevitable that some errors will have been introduced. Accents are a special problem, since they have to be individ ually re-inserted, and some will have been lost We have made corrections to spelling (including standardisation to UK spelling) - and to grammar where there were obvious problems with English usage. There has, however, been no scientific editing or vetting of the abstracts, other than removal \other nomina nuda. Some addresses have been shortened to save space, full postal addresses can be found in the INA Membership directory (INA Newsletter 14/3, p.118-124) The format adopted is virtually the same as for the Prague Abstract volume (INA Newsletter 13/2, 1991), including the use of topic codes similar to those used in the INA Bibliographies. These codes are (1) Age range covered. (2) Geographical provenance of studied material. (3) General topic of paper, N.B. -
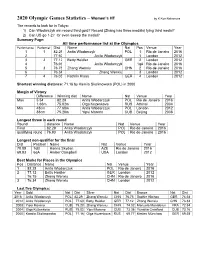
2020 Olympic Games Statistics
2020 Olympic Games Statistics – Women’s HT by K Ken Nakamura The records to look for in Tokyo: 1) Can Wlodarczyk win record third gold? Record (Zhang has three medals) tying third medal? 2) Can US go 1-2? Or even sweep the medal? Summary Page: All time performance list at the Olympics Performance Performer Dist Name Nat Pos Venue Year 1 1 82.29 Anita Wlodarczy k POL 1 Rio de Janeiro 2016 2 77.60 Anita Wlodarczyk 1 London 2012 3 2 77.12 Betty Heidler GER 2 London 2012 4 76.93 An ita Wlodarczyk 1qA Rio de J aneiro 2016 5 3 76.75 Zhang Wenxiu CHN 2 Rio de Janeiro 201 6 6 76.34 Zhang Wenxiu 3 London 2012 7 4 76.05 Kathrin Klaas GER 4 London 2012 Shortest winning distance: 71.16 by Kamila Skolimowska (POL) in 2000 Margin of Victory Difference Winning dist Name Nat Venue Year Max 5.54 82.29 Anita Wlodarczyk POL Rio de Janeiro 2016 1.66m 75.02m Olga Kuzenkova RUS Athinai 2004 Min 48cm 77.60 m Anita Wlodarc zyk POL Lon don 2012 88cm 75.20m Yipsi Moreno CUB Beijing 2008 Longest throw in each round Round distance Name Nat Venue Year Final 82.29 Anita Wlodarczyk POL Rio de Janeiro 2016 qualifying round 76.93 Anita Wlodarczyk POL Rio de Janeiro 201 6 Longest non-qualifier for the final Dist Position Name Nat Venue Ye ar 70.09 7qB Hanna Skydan AZE Rio de Janeiro 2016 69.93 6qA Amber Campbell USA London 2012 Best Marks for Places in the Olympics Pos Distance Name Nat Venue Year 1 82.29 Anita Wlodarczyk POL Rio de Janeiro 2016 2 77.12 Betty Heidler GER London 2012 76.75 Zhang Wenxiu CHN Rio de Janeiro 2016 3 76.34 Zhang Wenxiu CHN London 2012 Last five -

Almanac-2003.Pdf
www.athletics.org.au 2004 Season Guide TELSTRA A-SERIES & TELSTRA A-CHAMPIONSHIPS INCORPORATING THE 53rd YEAR OF RECORDS & RESULTS The 2004 Season Guide was produced by Athletics Australia (AA) Special thanks to the following people and organisations for their support and contributions to Athletics Australia and inparticular to this year’s guide: Rankings Paul Jenes, Dan Suchy and David Tarbotton Results Peter Hamilton Australian Championship Placegetters Peter Hamilton Records Ronda Jenkins Profiles David Tarbotton and Neil Fuller Telstra A-series Information AA Competitions Selection Criteria AA High Performance International Association of Athletics Federations (IAAF) Athletics Australia principal sponsor - Telstra Athletics Australia Sponsors and Supporters: New Balance, IGA, Accor, Qantas, Australian Sports Commission, Australian Olympic Committee, Australian Commonwealth Games Association, Australian Paralympic Committee. Official Photographers of Athletics Australia - Getty Images Pty Limited - Phone: 1800 550 285 Cover Image: Louise Sauvage speeds to victory in the women's 800m wheelchair final at the 2003 IAAF World Championships in Paris. P 1 IGA Advertisement Ausport Advertisement www.athletics.org.au 04Season Guide Contents Message from the Chairman of Athletics Australia PREFACE An Olympic Games year is the pinnacle year in any four-year cycle, and four years after Sydney, we are all looking forward Acknowledgements _______________________________________________________________1 to the Athens Games. Contents ______________________________________________________________________4 -

Men's 100M Final 30.06.2021
Men's 100m Final 30.06.2021 Start list 100m Time: 19:55 Records Lane Athlete Nat NR PB SB 1 Bartosz TARADAJ POL 10.00 10.77 10.79 WR 9.58 Usain BOLT JAM Olympiastadion, Berlin 16.08.09 2 Dominik BOCHENEK POL 10.00 10.91 AR 9.86 Francis OBIKWELU POR Olympic Stadium, Athina 22.08.04 3 Jerome BLAKE CAN 9.84 10.20 10.20 =AR 9.86 Jimmy VICAUT FRA Paris 04.07.15 =AR 9.86 Jimmy VICAUT FRA Montreuil-sous-Bois 07.06.16 4 Tlotliso Gift LEOTLELA RSA 9.89 9.94 9.94 NR 10.00 Marian WORONIN POL Warszawa 09.06.84 5 Michael RODGERS USA 9.69 9.85 10.09 WJR 9.97 Trayvon BROMELL USA Eugene, OR 13.06.14 6 Dominik KOPEĆ POL 10.00 10.25 10.29 MR 10.39 Simon MAGAKWE RSA 12.06.19 7Adrian BRZEZIŃSKIPOL10.0010.4610.47SB 9.77 Trayvon BROMELL USA Miramar, FL 05.06.21 8Karol KWIATKOWSKIPOL10.0010.4310.48 2021 World Outdoor list 9.77 +1.5 Trayvon BROMELL USA Miramar, FL (USA) 05.06.21 Medal Winners Previous Meeting 9.85 +1.5 Marvin BRACY USA Miramar, FL (USA) 05.06.21 9.85 +0.8 Ronnie BAKER USA Eugene, OR (USA) 20.06.21 2019 - IAAF World Ch. in Athletics Winners 9.86 +0.8 Fred KERLEY USA Eugene, OR (USA) 20.06.21 1. Christian COLEMAN (USA) 9.76 19 Simon MAGAKWE (RSA) 10.39 9.89 +0.2 Isiah YOUNG USA Clermont, FL (USA) 30.05.21 2. -

Abstract Book
3rd Annual International Conference on Earth and Environmental Sciences 2016 6-9 June 2016: Abstract Book Earth and Environmental Sciences Abstracts Third Annual International Conference on Earth and Environmental Sciences 6-9 June 2016, Athens, Greece Edited by Gregory T. Papanikos THE ATHENS INSTITUTE FOR EDUCATION AND RESEARCH 1 3rd Annual International Conference on Earth and Environmental Sciences 6-9 June 2016: Abstract Book 2 3rd Annual International Conference on Earth and Environmental Sciences 6-9 June 2016: Abstract Book Earth and Environmental Sciences Abstracts 3rd Annual International Conference on Earth and Environmental Sciences 6-9 June 2016, Athens, Greece Edited by Gregory T. Papanikos 3 3rd Annual International Conference on Earth and Environmental Sciences 6-9 June 2016: Abstract Book First Published in Athens, Greece by the Athens Institute for Education and Research. ISBN: 978-960-598-059-7 All rights reserved. No part of this publication may be reproduced, stored, retrieved system, or transmitted, in any form or by any means, without the written permission of the publisher, nor be otherwise circulated in any form of binding or cover. 8 Valaoritou Street Kolonaki, 10671 Athens, Greece www.atiner.gr ©Copyright 2015 by the Athens Institute for Education and Research. The individual essays remain the intellectual properties of the contributors. 4 3rd Annual International Conference on Earth and Environmental Sciences 6-9 June 2016: Abstract Book TABLE OF CONTENTS (In Alphabetical Order by Author's Family name) Preface 7 Conference Program 9 1. The Water Uses in the Multiple Actors' Representation: A Territorial Approach of Rio Doce's Medium Course 15 Watershed in Southwest Part of Goiás Franciane Araujo de Oliveira & Celene Cunha M. -

10Th IAAF World Championships in Athletics Helsinki (FIN) - Saturday, Aug 06, 2005 Shot Put - M QUALIFICATION Qual
------------------------------------------------------------------------------------- 10th IAAF World Championships in Athletics Helsinki (FIN) - Saturday, Aug 06, 2005 Shot Put - M QUALIFICATION Qual. rule: qualification standard 20.25m or at least best 12 qualified. ------------------------------------------------------------------------------------- Group A 06 August 2005 - 10:00 Position Bib Athlete Country Mark . 1 971 Christian Cantwell USA 21.11 Q . 2 200 Joachim Olsen DEN 20.85 Q . 3 75 Andrei Mikhnevich BLR 20.54 Q . 4 1012Adam Nelson USA 20.35 Q . 5 304 Tepa Reinikainen FIN 20.19 q . 6 727 Tomasz Majewski POL 20.12 q . 7 363 Carl Myerscough GBR 20.07 q . 8 774 Gheorghe Guset ROU 19.83 . 9 239 Manuel Martínez ESP 19.55 . 10 194 Petr Stehlík CZE 19.48 . 11 853 Miran Vodovnik SLO 19.28 . 12 838 Ivan Yushkov RUS 18.98 . 13 143 Marco Antonio Verni CHI 18.60 . 14 509 Dorian Scott JAM 18.33 . 840 Shaka Sola SAM DNS . Athlete 1st 2nd 3rd Christian Cantwell 21.11 Joachim Olsen 20.16 19.82 20.85 Andrei Mikhnevich 20.54 Adam Nelson X 20.35 Tepa Reinikainen 19.87 20.19 20.06 Tomasz Majewski 20.04 20.12 20.09 Carl Myerscough 19.88 20.07 19.68 Gheorghe Guset 19.44 19.60 19.83 Manuel Martínez 19.49 19.55 19.28 Petr Stehlík 18.98 19.48 X Miran Vodovnik 18.60 18.58 19.28 Ivan Yushkov 18.77 18.98 X Marco Antonio Verni X X 18.60 Dorian Scott 18.10 X 18.33 Shaka Sola Group B 06 August 2005 - 10:00 Position Bib Athlete Country Mark . -

Qualification START LIST Hammer Throw WOMEN Karsintakilpailu
10th IAAF World Championships in Athletics Helsinki From Saturday 6 August to Sunday 14 August 2005 Hammer Throw WOMEN Moukarinheitto NAISET ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHL Qualification START LIST Karsintakilpailu OSANOTTAJALUETTELO ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETI Qualification standard 70.00 or at least best 12 qualified 1 2 Group A 10 August 2005 14:00 Ryhmä A START BIB COMPETITOR NAT YEAR Personal Best 2005 Best 1 567 Kamila SKOLIMOWSKA POL 82 74.27 74.27 2 300 Betty HEIDLER GER 83 72.73 72.19 3 7 Jennifer DAHLGREN ARG 84 67.07 67.07 4 231 Sini PÖYRY FIN 80 69.16 68.90 5 594 Mihaela MELINTE ROM 75 76.07 71.95 6 711 Cecilia NILSSON SWE 79 68.44 68.44 7 56 Darya PCHELNIK BLR 81 71.08 71.08 8 796 Bethany HART USA 77 69.65 69.65 9 122 Wenxiu ZHANG CHN 86 73.24 73.24 10 306 Kathrin KLAAS GER 84 70.91 70.91 11 648 Tatyana LYSENKO RUS 83 77.06 77.06 12 155 Yipsi MORENO CUB 80 75.18 73.88 13 350 Éva ORBÁN HUN 84 68.70 68.70 14 181 Berta CASTELLS ESP 84 68.87 68.31 15 770 Nataliya ZOLOTUKHINA UKR 85 69.73 67.75 16 638 Yekaterina KHOROSHIKH RUS 83 73.08 73.08 17 373 Clarissa CLARETTI ITA 80 70.59 70.59 Issued Tuesday, 09 August 2005 at 11:01 Timing and Measurement by SEIKO Data processing -

2016 Olympic Games Statistics – Women's HT
2016 Olympic Games Statistics – Women’s HT by K Ken Nakamura The records to look for in Rio de Janeiro: Olympic record, largest winning margin, and longest throw in Rio are all under threat by Wlodarczyk Summary Page: All time performance list at the Olympics Performance Performer Dist Name Nat Pos Venue Year 1 1 78.18 Tatyana Beloborodova Lysenko RUS 1 London 2012 2 2 77.60 Anita Wlodarczyk POL 2 London 2012 3 3 77.12 Betty Heidler GER 3 London 2012 4 4 76.34 Aksana Miankova BLR 1 Beijing 2008 4 4 76.34 Zhang Wenxiu CHN 4 London 2012 6 6 76.05 Kathrin Klaas GER 5 London 2012 Shortest winning distance: 71.16 by Kamila Skolimowska (POL) in 2000 Margin of Victory Difference Winning dist Name Nat Venue Year Max 1.66m 75.02m Olga Kuzenkova RUS Athinai 2004 Min 58cm 78.18m Tatyana Lysenko RUS London 2012 1.14m 76.34m Aksana Miankova BLR Beijing 2008 Longest throw in each round Round distance Name Nat Venue Year Final 78.18 Tatyana Lysenko RUS London 2012 qualifying round 75.68 Anita Wlodarczyk POL London 2012 Longest non-qualifier for the final Dist Position Name Nat Venue Year 69.93 6qA Amber Campbell USA London 2012 Best Marks for Places in the Olympics Pos Distance Name Nat Venue Year 1 78.18 Tatyana Lysenko RUS London 2012 76.34 Aksana Miankova BLR Beijing 2008 2 77.60 Anita Wlodarczyk POL London 2012 75.20 Yipsi Moreno CUB Beijing 2008 3 77.12 Betty Heidler GER London 2012 74.32 Zhang Wenxiu CHN Beijing 2008 4 76.34 Zhang Wenxiu CHN London 2012 Multiple Medalists: Yipsi Moreno (CUB): 2004 Silver, 2008 Silver Olga Kuzenkova (RUS): 2000 -

Hammer Throwing
Hammer Throwing Bob Wagner 2006 draft 16/12/06 [email protected] http://www.hammerthrowing.com.au 2 CONTENTS THE AUTHOR.....................................................................................................................................................................4 INTRODUCTION ................................................................................................................................................................5 WORLD RECORD PROGRESSION.................................................................................................................................6 Men..............................................................................................................................................................................6 Women ........................................................................................................................................................................6 WEIGHT THROWING ........................................................................................................................................................7 A HISTORY OF HAMMER THROWING IN AUSTRALIA................................................................................................8 Men..............................................................................................................................................................................8 Women .................................................................................................................................................................... -

Japão 25 De Agosto a 03 De Setembro De 2007
11º Campeonatos Mundiais de Atletismo Adulto Osaka – Japão 25 de agosto a 03 de setembro de 2007 Official Results - Marathon - M - Final 25 august 2007 - 7:00 Pos Bib Athlete Country Mark 1 15 Luke Kibet KEN 2:15:59 2 4 Mubarak Hassan Shami QAT 2:17:18 3 9 Viktor Röthlin SUI 2:17:25 4 73 Yared Asmerom ERI 2:17:41 5 29 Tsuyoshi Ogata JPN 2:17:42 (SB) 6 30 Satoshi Osaki JPN 2:18:06 (SB) 7 14 Toshinari Suwa JPN 2:18:35 (SB) 8 10 William Kiplagat KEN 2:19:21 9 49 Janne Holmén FIN 2:19:36 10 22 José Manuel Martínez ESP 2:20:25 11 59 Dan Robinson GBR 2:20:30 12 47 Alex Malinga UGA 2:20:36 13 33 Tomoyuki Sato JPN 2:20:53 14 8 Gashaw Asfaw ETH 2:20:58 15 79 Ju-Young Park KOR 2:21:49 16 56 Mike Fokoroni ZIM 2:21:52 17 18 José Ríos ESP 2:22:21 (SB) 18 60 José de Souza BRA 2:22:24 19 81 Seteng Ayele ISR 2:22:27 (SB) 20 66 Ali Mabrouk El Zaidi LBA 2:22:50 21 45 Mbarak Kipkorir Hussein USA 2:23:04 (SB) 22 50 Alberto Chaíça POR 2:23:22 (SB) 23 70 Mike Morgan USA 2:23:28 (SB) 24 76 Young Chun Kim KOR 2:24:25 25 27 Samson Ramadhani TAN 2:25:51 26 65 Myongseung Lee KOR 2:25:54 27 2 Hendrick Ramaala RSA 2:26:00 28 82 Chia-Che Chang TPE 2:26:22 29 75 Khalid Kamal Yaseen BRN 2:26:32 (SB) 30 28 Getuli Bayo TAN 2:26:56 31 12 Dejene Birhanu ETH 2:27:50 (SB) 32 72 Kyle O'Brien USA 2:28:28 (SB) 33 64 Wei Su CHN 2:28:41 (SB) 34 85 Wodage Zvadya ISR 2:29:21 35 54 Luís Feiteira POR 2:29:34 36 32 Haiyang Deng CHN 2:29:37 (SB) 37 86 Ulrich Steidl GER 2:30:03 38 17 Ambesse Tolosa ETH 2:30:20 39 78 Michael Tluway Mislay TAN 2:30:33 40 83 Asaf Bimro ISR 2:31:34 41 53 -

President's Message
UPDATE Newsletter of the European Athletic Association 3|04 December President‘s Message HANSJÖRG WIRZ begun to transform our organisation. We started by moving our Head Office As in any business, the success of a sport to Lausanne and increasing the available movement like ours requires constant working capacity to meet the new de- adaptation to the changing expectations mands. To increase our control over our of society in general and the customer in marketing rights, we have changed our particular. The first priority for European structure for managing them. To help 2 CONTEST Athletics is, of course, that our athletes increase the recognition of European Ath- Waterford Crystal European have the chance to practice the sport and letics and create additional value for our Athlete of the Year Trophy 04 can participate in a well-structured system sport, we created a new brand architec- that provides them with the appropriate ture that visually links all our activities. To 5 STATISTICS level of competition. But it is also impor- improve our operational efficiency, we tant to understand and meet the needs adapted our internal structure and we will The Europeans in the top 100 of other groups touched by our sport, for propose constitutional changes for con- example spectators in the stadium and tel- sideration by the next EAA Congress. To 8 INSIDE evision viewers. increase the input of ideas and know how In memoriam EAA honorary from our Member Federations, we created member Artur Takac The year 2004 has underlined the impor- a system of working groups. To improve tance of these facts.