Monetary Policy in a Monetary Union: What Role for Regional Information?∗
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Payments and Market Infrastructure Two Decades After the Start of the European Central Bank Editor: Daniela Russo
Payments and market infrastructure two decades after the start of the European Central Bank Editor: Daniela Russo July 2021 Contents Foreword 6 Acknowledgements 8 Introduction 9 Prepared by Daniela Russo Tommaso Padoa-Schioppa, a 21st century renaissance man 13 Prepared by Daniela Russo and Ignacio Terol Alberto Giovannini and the European Institutions 19 Prepared by John Berrigan, Mario Nava and Daniela Russo Global cooperation 22 Prepared by Daniela Russo and Takeshi Shirakami Part 1 The Eurosystem as operator: TARGET2, T2S and collateral management systems 31 Chapter 1 – TARGET 2 and the birth of the TARGET family 32 Prepared by Jochen Metzger Chapter 2 – TARGET 37 Prepared by Dieter Reichwein Chapter 3 – TARGET2 44 Prepared by Dieter Reichwein Chapter 4 – The Eurosystem collateral management 52 Prepared by Simone Maskens, Daniela Russo and Markus Mayers Chapter 5 – T2S: building the European securities market infrastructure 60 Prepared by Marc Bayle de Jessé Chapter 6 – The governance of TARGET2-Securities 63 Prepared by Cristina Mastropasqua and Flavia Perone Chapter 7 – Instant payments and TARGET Instant Payment Settlement (TIPS) 72 Prepared by Carlos Conesa Eurosystem-operated market infrastructure: key milestones 77 Part 2 The Eurosystem as a catalyst: retail payments 79 Chapter 1 – The Single Euro Payments Area (SEPA) revolution: how the vision turned into reality 80 Prepared by Gertrude Tumpel-Gugerell Contents 1 Chapter 2 – Legal and regulatory history of EU retail payments 87 Prepared by Maria Chiara Malaguti Chapter 3 – -
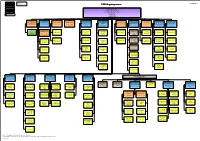
ECB Organisational Chart
Executive Board DG= Director General D= Director ECB PUBLIC Directorate General Dep./Deps.= Deputies ECB Organigramme Directorate Division Executive Board Other Units Christine Lagarde - President Luis de Guindos - Vice President Centre Fabio Panetta Frank Elderson Reporting line Philip R. Lane Isabel Schnabel Principal Macroprudential Market Infrastructure Legal Services Coordinator of the ESRB Secretariat Communications Policy & Financial International & Secretariat Internal Audit Risk Management Banknotes & Payments Counsel to the Stability European Relations DG: Wolfgang Proissl DG: Chiara Zilioli D: Francesco Mazzaferro Executive Board DG: Petra Senkovic D: Claudia Mann Deps.: Thierry Bracke DG: Ulrich Bindseil Deps.: Christian Dep.: Tuomas Peltonen DG: Sergio Nicoletti-Altimari D: Fernando Monar Lora DG: Hans-Joachim Klöckers D: Ton Roos Conny Lotze Deps.: Dimitri Pattyn Kroppenstedt Deps.: John Fell Dep.: Livio Stracca D: Roland Straub Fiona van Echelpoel Roberto Ugena Fátima Pires Compliance and ECB Representative Climate Change Centre Governance Office** Global Media Systemic Risk & Office in Brussels Currency Audit Missions Risk Strategy Oversight Institutional Law Senior Adviser: Irene Relations Financial Development Heemskerk Chief Compliance and Principal Adviser: Boris Institutions Governance Officer: Roman Kisselevsky Schremser ECB Representation in Washington D.C. Audit Support & Currency Market Innovation Web & Digital Stress Test Risk Analysis Principal Adviser: Financial Law Information Investigations Management & Integration -

Válogatás a Nemzetközi Intézmények És Külföldi Jegybankok Publikációiból
NEMZETKÖZI SZEMELVÉNYEK Válogatás a nemzetközi intézmények és külföldi jegybankok publikációiból 2020. november 26. – december 02. 26. 1 TARTALOMJEGYZÉK 1. MONETÁRIS POLITIKA, INFLÁCIÓ ................................................................................................... 3 2. PÉNZÜGYI STABILITÁS, PÉNZÜGYI PIACOK .................................................................................... 4 3. MIKROPRUDENCIÁLIS FELÜGYELET ÉS SZABÁLYOZÁS ................................................................... 5 4. FINTECH, KRIPTOVALUTÁK, MESTERSÉGES INTELLIGENCIA .......................................................... 6 5. ZÖLD PÉNZÜGYEK, FENNTARTHATÓ FEJLŐDÉS ............................................................................. 8 6. PÉNZFORGALOM, FIZETÉSI RENDSZEREK ....................................................................................... 9 7. MAKROGAZDASÁG ....................................................................................................................... 10 8. ÁLTALÁNOS GAZDASÁGPOLITIKA ................................................................................................ 11 9. KÖLTSÉGVETÉSI POLITIKA, ADÓZÁS ............................................................................................. 12 10. SZANÁLÁS .................................................................................................................................. 14 11. STATISZTIKA ............................................................................................................................. -

What Doesn't Kill Us Makes Us Stronger: but Can the Same Be Said of the Eurozone?
What Doesn't Kill Us Makes Us Stronger: But Can the Same Be Said of the Eurozone? CAROLITE JENSEN* This comment provides a brief, analytical survey of the European sovereign debt crisis. It aims to be user-friendly and accessible to any reader who wants to learn more about the causes and consequences of Europe's ongoing troubles. Rather than focus on a particular country, the comment reviews the fiscal Eurozone and its banking system as a whole. It begins by explaining the key, long-term roots of the Eurozone's present problems. Then, it provides a critical commentary on attempted reforms, and an analysis of the events that have unfolded this past year. It concludes by evaluating the Eurozone's options for fiscal and structural reform going forward. I. Introduction The Eurozone sovereign debt crisis is a moving target. Among other things, its roots are traceable to the 2008 financial crisis, flawed political constructs, risky and dishonest business practices, and faulty economic models. To the lay observer trying to make sense of the crisis, the avalanche of news on politicians, banks, and private market players can overwhelm and obscure. But it is important to wrestle with and understand these issues. The collective Eurozone is one of the world's largest economies. The debt crisis is rapidly evolving, and whatever happens in the next few years, for good or for ill, will affect everyone. This paper tackles the issue from a particular angle. It discusses the more significant legal changes occurring within the banking sector in response to the crisis, as well as external legal changes that will impact the banking sector. -

ECB: Unexpected Shake-Up Snap the German Member of the ECB’S Executive Board, Sabine Lautenschläger, Just Announced Her Resignation from Office by the End of October
Economic and Financial Analysis 25 September 2019 ECB: Unexpected shake-up Snap The German member of the ECB’s Executive Board, Sabine Lautenschläger, just announced her resignation from office by the end of October ECB headquarters, Frankfurt This is another shake-up of the ECB. Sabine Lautenschläger has announced that she will resign from office by the end of October. Lautenschläger has been on the ECB’s Executive Board since 27 January 2014, when she succeeded Jörg Asmussen, who back then left the ECB for a position in the German government. Her eight-year term would normally end in January 2022. Lautenschläger has been mainly responsible for setting up the Single Supervisory Mechanism (SSM). No reasons for her resignation were given in the press statement. So far, the motivation for her resignation is unclear. It may be due to personal reasons but perhaps also a protest against the ECB’s recent decision to engage in another round of monetary easing. The latter would fit into an almost typical German tradition as previous Executive Board member Jürgen Stark and Bundesbank President Axel Weber both stepped down in protest. Sabine Lautenschläger has been the most vocal and often the only member of the Executive Board to publicly criticise the ECB’s bond purchases. Some commentators had also expected her to be in the race for chair of the SSM, which eventually went to the Italian Andrea Enria. Lautenschläger will now be the fifth Executive Board member to resign before the official term ends. • The first ECB President Wim Duisenberg resigned in 2003 to make way for Jean-Claude Trichet • Lorenzo Bini Smaghi resigned in 2011, leaving only one Italian national on the Board after Mario Draghi had become president. -

List of Speakers
SPEAKERS Wednesday, 1 July 2020 Welcome Address Werner Hoyer has a PhD (in economics) from Cologne University where he also started his career in various positions. Dr Hoyer served for 33 years as a Member of the German Bundestag. During this period, he held the position of Minister of State at the Foreign Office on two separate occasions. In addition, he held several other positions, including that of Whip and FDP Security Policy Spokesman, Deputy Chairman of the German-American Parliamentary Friendship Group, FDP Secretary General and President of the European Liberal Democratic Reform Party (ELDR). Upon appointment by the EU Member States, Dr Hoyer commenced his first term as EIB President in January 2012. His mandate was renewed for a second term commencing on 1 January 2018. Dr Hoyer and his wife Katja have two children. Werner Hoyer President, European Investment Bank Klaus Regling is the current and first Managing Director of the European Stability Mechanism. The Managing Director of the ESM is appointed by the Board of Governors for a renewable term of five years. Klaus Regling is also the CEO of the European Financial Stability Facility (EFSF), a position he has held since the creation of the EFSF in June 2010. Klaus Regling has worked for over 40 years as an economist in senior positions in the public and the private sector in Europe, Asia, and the U.S., including a decade with the IMF in Washington and Jakarta and a decade with the German Ministry of Finance where he prepared Economic and Monetary Union in Europe. -

Recent Events
Web Version | Update preferences | Unsubscribe Forward Newsletter 03/2016 (No.19) RECENT EVENTS • RECENT EVENTS • OPPORTUNITIES • WORKING PAPERS • POLICY BRIEFS & COMMENTARIES • IN THE PRESS Villa Emiliani Carlo Bastasin introducing Marcello Messori, Gianni William Drozdiak at Fractured Toniolo, and SEP Researchers Continent Europe's Crises at Fractured Continent and the Fate of the West Europe's Crises and the Fate of the West UPCOMING EVENTS April 4, 2016 Peter Praet: Una nuova governance per l’euro un passo indietro o uno in avanti per la Bce? April 13, 2016 Luigi Abete: Perché le imprese italiane hanno perso produttività? April 20, 2016 Lorenzo Fabio Panetta and Fabrizio Marcello Messori and SEP Bini Smaghi: Riforme o Saccomanni at Banking Union Researchers at Banking Union declino? La sfida della secular stagnation all'Europa May 4, 2016 Alessandro Profumo: Perché le banche italiane sono diverse da quelle europee? May 11, 2016 Pier Carlo Padoan: A quanta sovranità si può rinunciare? L'ora del governo europeo May 18, 2016 Giuseppe Buccino: La sfida dell'immigrazione May 26, 2016 Tito Boeri: Il futuro del lavoro Marcello Messori and Gian Stefano Micossi and MEEG Luigi Tosato at Implicazioni Students at Implicazioni PAST EVENTS giuridiche del negoziato su giuridiche del negoziato su Brexit Brexit March 22, 2016 William Drozdiak: Fractured Continent Europe's OPPORTUNITIES Crises and the Fate of the West Visiting Fellowships March 18, 2016 Fabio Panetta: Banking Union The LUISS School of European Political Economy invites applications for Senior and Junior Fellowships tenable in the academic year 2015 March 1, 2016 Gian 16 (September 2016 – June 2017). -

Perspectives and Implications for Financial Markets
Munich Personal RePEc Archive Tracking ECB’s communication: Perspectives and Implications for Financial Markets FORTES, Roberta and Le Guenedal, Theo December 2020 Online at https://mpra.ub.uni-muenchen.de/108746/ MPRA Paper No. 108746, posted 22 Jul 2021 06:50 UTC Tracking ECB’s Communication: Perspectives and implications for financial markets Roberta Fortes✯ Th´eo Le Guenedal∗ Ph.D. Candidate Quantitative Analyst Paris 1 Panth´eon-Sorbonne, Paris Amundi Asset Management, Paris December 2020 Abstract This article assesses the communication of the European Central Bank (ECB) using Natural Language Processing (NLP) techniques. We show the evolution of discourse over time and capture the main themes of interest for the central bank that go beyond its traditional mandate of maintaining price stability, enlightening main concerns and themes of discussion among board members. We also built sentiment signals compatible with any form of language, both formal and informal, an important step as the ECB aims to enhance communication with non-expert audiences. In a second step, we measure the impact of the ECB’s communication on the EUR/USD exchange rate. We found that our quantitative series, both topics and sentiment, improve financial-linked models consistently in all periods analyzed (2.5% on average). Meaningful signals comprise a broad range of subjects and vary in time. This suggests that overall ECB’s talk matters for asset prices, including themes not directly related to monetary policy. This result is particularly important in a context in which the ECB, as well as other major central banks, are moving towards integrating issues closer to the society into their scope of action, implying that subjects, which were considered peripheral, may become central. -
21St Century Cash: Central Banking, Technological Innovation and Digital Currencies*
SUERF Policy Note Issue No 40, August 2018 21st century cash: Central banking, technological innovation and digital currencies* By Fabio Panetta1 Deputy Governor of the Bank of Italy JEL-codes: E42, E51, E58, G21, O33 . Keywords: technological progress, money, central banks, digital currency, payments system, financial stability, monetary policy, anonymity . Technological progress is allowing for the digitization of many objects of our daily life. Cash may be next in line. The paper analyses the pros and cons of issuing a Central Bank Digital Currency (CBDC), a dematerialized liability of the central bank accessible by anyone in the economy. While recourse to a CBDC as a means of payments may well have benefits, their precise nature is uncertain and they may be too small to justify the introduction of a CBDC. A digital currency could increase financial instability risks, due to its potential effects on the demand for commercial bank deposits; however its impact on the banking system is unlikely to be disruptive. Overall the case for issuing a CBDC remains at best unclear. In addition, a digital currency introduces many open questions, like the role and footprint of central banks in the economy and the extent to which it should preserve anonymity in transactions. Especially the latter implies that the decision to issue a CBDC is hardly a technical one: society as a whole must be involved. * The Policy Note is based on a speech held by Fabio Panetta on the occasion of the SUERF/BAFFI CAREFIN Centre Conference on "Do we need central bank digital currency? Economics, Technology and Institutions" in Milan, on 7 June 2018. -

Institutional Corruption in Finance and Organisational Solutions Against
Master Thesis Institutional Corruption in Finance and Organisational Solutions Against Losing Ascribed Purpose carried out for the purpose of obtaining the degree of Master of Science, submitted at TU Wien, Faculty of Mechanical and Industrial Engineering Berk Çaycı Mat.Nr.: 00826972 under the supervision of Em. O. Univ.Prof. Dipl.-Ing. Dr. techn Adolf Stepan Institute for Management Science- Work Science and Organisation Vienna, June 2020 Berk Çaycı I declare in lieu of oath, that I wrote this thesis and performed the associated research myself, using only literature cited in this volume. If text passages from sources are used literally, they are marked as such. I confirm that this work is original and has not been submitted elsewhere for any examination, nor is it currently under consideration for a thesis elsewhere. Place and Date Signature Acknowledgements I would like to thank my supervisor Em. O. Univ.Prof. Dipl.-Ing. Dr. techn Adolf Stepan for sharing his insight about institutional corruption. His valuable suggestions helped me to advance my thoughts on the subject and create a better analysis. Moreover, I would like to thank Manca Jurca for proofreading. I am also very grateful for my family and my girlfriend who provided support during the composition of this thesis, including quarantine days of Covid-19 pandemic. Kurzfassung Institutionelle Korruption ist ein Konzept, das entwickelt wurde, um schlecht funktionierende Organisationen aus einer neuen Perspektive zu analysieren. Organisationen können von ihrem Zweck abweichen und ihr öffentliches Vertrauen verlieren, obwohl es keine Anzeichen für individuelle Korruption gibt. Institutionelle Korruption tritt auf, wenn ein rechtlicher, sogar derzeit ethischer Einfluss die Wirksamkeit einer Organisation schwächt und ihr öffentliches Vertrauen schädigt. -

Monetary Policy and the Independence of Central Banks: the Experience of the European Central Bank in the Global Crisis
Università degli Studi di Verona Monetary policy and the independence of central banks: the experience of the European Central Bank in the global crisis Speech by Salvatore Rossi Senior Deputy Governor of the Bank of Italy Complesso universitario di Vicenza 19 November 2014 1. The independence of central banks in theory and in history1 We have been talking about the independence of central banks almost from the time of their inception. In an essay of 1824 David Ricardo accused the Bank of England, founded more than a century earlier, of submitting to the power of the executive. 2 Ricardo identified the three pillars of central bank independence: institutional separation of the power to create money from the power to spend it; a ban on the monetary funding of the State budget; and the central bank’s obligation to give an account of its monetary policy. Ricardo’s suggestions were taken up by the Brussels Conference of 1920, held under the aegis of the League of Nations with the aim of identifying the best policies to counter the economic and financial crisis that followed the First World War. Price stability was indicated as the primary objective of monetary policy but – as the Final Report of the conference maintained – if it was to be achieved, it had to be entrusted to central banks that were independent of their governments.3 These principles were forgotten for many years after the Second World War. The conviction that a certain degree of inflation was necessary to support employment and growth came to the fore in economic thought and in the minds of policy makers. -

Tracking ECB's Communication
Working Paper 106-2021 I February 2021 Tracking ECB’s Communication: Perspectives and Implications for Financial Markets Document for the exclusive attention of professional clients, investment services providers and any other professional of the financial industry Tracking ECB’s Communication: Perspectives and Implications for Financial Markets Abstract Roberta Fortes This article assesses the communication of the European University of Paris 1 Central Bank (ECB) using Natural Language Processing Panthéon Sorbonne (NLP) techniques. We show the evolution of discourse over [email protected] time and capture the main themes of interest for the central bank that go beyond its traditional mandate of maintaining Théo Le Guenedal price stability, enlightening main concerns and themes of Quantitative Research discussion among board members. We also built sentiment [email protected] signals compatible with any form of language, both formal and informal, an important step as the ECB aims to enhance communication with non-expert audiences. In a second step, we measure the impact of the ECB’s communication on the EUR/USD exchange rate. We found that our quantitative series, both topics and sentiment, improve financial-linked models consistently in all periods analyzed (2.5% on average). Meaningful signals comprise a broad range of subjects and vary in time. This suggests that overall ECB’s talk matters for asset prices, including themes not directly related to monetary policy. This result is particularly important in a context in which the ECB, as well as other major central banks, are moving towards integrating issues closer to the society into their scope of action, implying that subjects, which were considered peripheral, may become central.