DOCSLIB.ORG

Computational Interior Ballistics Modeling Robert Miner

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Computational Interior Ballistics Modeling Robert Miner University of New Mexico UNM Digital Repository Mechanical Engineering ETDs Engineering ETDs 1-30-2013 Computational interior ballistics modeling Robert Miner Follow this and additional works at: https://digitalrepository.unm.edu/me_etds Recommended Citation Miner, Robert. "Computational interior ballistics modeling." (2013). https://digitalrepository.unm.edu/me_etds/68 This Thesis is brought to you for free and open access by the Engineering ETDs at UNM Digital Repository. It has been accepted for inclusion in Mechanical Engineering ETDs by an authorized administrator of UNM Digital Repository. For more information, please contact [email protected]. Robert Todd Miner Candidate MECHANICAL ENGINEERING Department This thesis is approved, and it is acceptable in quality and form for publication: Approved by the Thesis Committee: Arslan Razani Ph.D. , Chairperson John Russell Ph.D. Steven Todd Ph.D. i Computational Interior Ballistics Modeling BY Robert Todd Miner* *BSME, University of New Mexico, 2008 THESIS Submitted in Partial Fulfillment of the Requirements for the Degree of Master of Science Mechanical Engineering The University of New Mexico Albuquerque, New Mexico December, 2012 ii DEDICATION I would like to dedicate this paper to my parents who have always been there for me and provided me the opportunity to further my education. This would not have been possible without their love and support. iii ACKNOWLEDGMENTS I would like to acknowledge my adviser Dr. Razani and my colleagues at Sandia National Laboratories. I would like to extend special thanks to my mentors Mark Anderson, Chance Hughs, and Steven Todd for making this research possible along with their expertise and support. In addition, I would also like to thank Greg Scharrer, Charles Jensen, Shawn Parks, the whole 5436 and 5437 teams for their support and guidance through my research and college years. Special thanks to my committee members, Dr. John Russell, Dr. Arslan Razani and Dr. Steven Todd for their valuable recommendations pertaining to this study and assistance in my professional development. iv Computational Interior Ballistics Modeling Robert Todd Miner* *BSME University of New Mexico, 2008 M.S., Mechanical Engineering, University of New Mexico, 2012 ABSTRACT Interior ballistics are the events in a gun system that determines the performance of any gun design. In order to efficiently design any gun system the internal ballistics should be understood to minimize energy losses and correctly define design parameters. The goal of this computational model is to develop a ballistics model to aid in gun design. A computational analysis of the dynamics events aids in the design of the gun system by providing output information such as pressure, velocity, charge burnout, and projectile distance versus time profiles. By applying the chemical and physical parameters of the propellant, gun breech geometry, projectile mass and gun barrel parameters, one can iterate through design parameters in an attempt to improve gun performance. There will be several computational models describing the main program being a lumped parameter internal ballistics analysis. The muzzle velocity of the model has been validated with empirical testing to at least one gun system and being applied to other gun systems for further validation on different designs. The validation of the muzzle velocity and breech pressure will build confidence in the model and allow for the model to be further developed into a more user friendly program. v TABLE OF CONTENTS DEDICATION ................................................................................................................... iii ACKNOWLEDGMENTS ................................................................................................ iv ABSTRACT ....................................................................................................................... v CHAPTER 1 INTRODUCTION ........................................................................................ 1 1.0 Introduction ............................................................................................................. 1 CHAPTER 2 INTERIOR BALLISTIC MODELING ........................................................ 3 2.0 Ballistics Problem ................................................................................................... 3 2.1 Pressure-Travel Curve ............................................................................................ 3 2.1.1 Propellant Parameters ......................................................................................... 5 2.1.2 Gun Parameters ................................................................................................. 12 2.1.3 Projectile Parameters ........................................................................................ 13 2.2 Numerical Techniques .......................................................................................... 14 2.2.1 Chemical Equilibrium Calculations .................................................................. 14 2.2.2 Closed Bomb Formulation ................................................................................. 18 2.2.3 Corner’s Model .................................................................................................. 21 2.2.4 Coppock's Model ................................................................................................ 23 2.2.5 IBHVG2 Lumped Parameter Model .................................................................. 36 2.2.6 XKTC Lumped Parameter Model and Codes of other Countries ...................... 38 2.2.7 SNL Lumped Parameter Model ......................................................................... 38 CHAPTER 3 MODEL COMPARISON ........................................................................... 48 3.1 Gun Models ........................................................................................................... 48 3.2 PAN Disruptor ...................................................................................................... 49 vi 3.3. 0.50 Caliber Powder Gun (SNL) ........................................................................ 55 3.3.1 SNL Powder Gun - .308 Winchester IMR 4350 .......................................... 57 3.3.2 SNL Powder Gun--.380 Winchester IMR 4064 ............................................ 60 3.3.5 SNL Powder Gun- 0.50 BMG IMR 4350 .................................................... 66 3.3.6 SNL Powder Gun- 0.50 BMG IMR 4064 ..................................................... 68 3.4 Thunder Range Powder Gun Results .................................................................... 70 3.5 50 mm Launcher ................................................................................................... 71 3.5.1- 50 mm Launcher Low Velocity Target ...................................................... 72 3.5.2-50 mm High Velocity Target ........................................................................ 74 CHAPTER 4 DISCUSSION ............................................................................................. 76 4.1 Model Difficulties .................................................................................................. 76 4.2 Model Limitations ................................................................................................. 76 CHAPTER 5 CONCLUSIONS ........................................................................................ 76 5.1 Summary ............................................................................................................... 76 5.2 Lessons Learned .................................................................................................... 77 5.3 Future Work .......................................................................................................... 78 REFERENCES ................................................................................................................. 79 APPENDIX A ................................................................................................................... 81 Propellant Formulations ............................................................................................. 82 APPENDIX B ................................................................................................................... 86 Corners Method: Mathcad Numeric Modeling ........................................................... 86 APPENDIX C ................................................................................................................... 92 Coppocks Method: Mathcad Numeric Modeling ........................................................ 92 vii APPENDIX D ................................................................................................................... 94 Lumped Parameter Model: Mathcad Numeric Modeling ........................................... 94 viii LIST OF FIGURES Figure 1. Propellant Grain Geometries ............................................................................... 6 Figure 2. Pressure vs. Grain Size ....................................................................................... 7 Figure 3. Pressure vs. Burn Type ....................................................................................... 8 Figure 4. Pressure vs. Load Density .................................................................................. 8 Figure 5. Velocity Dependence vs. Ballistic Parameters ................................................
Load more

Recommended publications
  • STANDARD OPERATING PROCEDURES Revision 10.0
    STANDARD OPERATING PROCEDURES Revision 10.0 Effective: November 10, 2020 Contents GTGC ADMINISTRATIVE ITEMS ............................................................................................................................................... 2 GTGC BOARD OF DIRECTORS: ............................................................................................................................................. 2 GTGC CHIEF RANGE SAFETY OFFICERS: ............................................................................................................................... 2 CLUB PHYSICAL ADDRESS: ................................................................................................................................................... 2 CLUB MAILING ADDRESS: .................................................................................................................................................... 2 CLUB CONTACT PHONE NUMBER ....................................................................................................................................... 2 CLUB EMAIL ADDRESS: ........................................................................................................................................................ 2 CLUB WEB SITE: ................................................................................................................................................................... 2 HOURS OF OPERATION ......................................................................................................................................................
    [Show full text]
  • Firearm Evidence
    INDIANAPOLIS-MARION COUNTY FORENSIC SERVICES AGENCY Doctor Dennis J. Nicholas Institute of Forensic Science 40 SOUTH ALABAMA STREET INDIANAPOLIS, INDIANA 46204 PHONE (317) 327-3670 FAX (317) 327-3607 EVIDENCE SUBMISSION GUIDELINE FIREARMS EVIDENCE INTRODUCTION Generally, crimes of violence involve the use of a firearm. The value of firearms and fired ammunition evidence will depend, to a significant degree on the recovery and submission techniques employed at the shooting event or later during autopsy. Trace evidence adhering to surfaces should be collected and submitted to the appropriate agency. This submission guideline is designed to assist you in your laboratory examination request decisions. Any situation not sufficiently explained to your specific needs may be handled on an individual basis by contacting the laboratory at (317) 327-3670 or the Firearms Section Supervisor at (317) 327-3777. A. The following is a list of items most commonly submitted to the Firearms Section for analyses: 1. Firearms 2. Cartridge Cases 3. Cartridges 4. Fired Bullets / Fragments 5. Shotshells 6. Wads 7. Slug / Pellets 8. Victim’s Clothing B. The I-MCFSA Firearms Section can conduct the following analysis: 1. Examination of firearms for function and safety, including test firing in order to obtain test bullets, cartridge cases and shot shells. 2. Comparison of evidence bullets, fired cartridge cases and shot shells to determine if they were or were not fired by the same firearm or the submitted firearm. 3. Examination of fired bullets to potentially determine caliber and possible make and type of firearm involved. 4. Imaging and comparing fired cartridge cases and test shots from firearms to similar exhibits recovered in unsolved crimes utilizing the NIBIN system (see NIBIN Submission Guideline #14).
    [Show full text]
  • Presentation Ballistics
    An Overview of Forensic Ballistics Ankit Srivastava, Ph.D. Assistant Professor Dr. A.P.J. Abdul Kalam Institute of Forensic Science & Criminology Bundelkhand University, Jhansi – 284128, UP, India E-mail: [email protected] ; Mob: +91-9415067667 Ballistics Ballistics It is a branch of applied mechanics which deals with the study of motion of projectile and missiles and their associated phenomenon. Forensic Ballistics It is an application of science of ballistics to solve the problems related with shooting incident(where firearm is used). Firearms or guns Bullets/Pellets Cartridge cases Related Evidence Bullet holes Damaged bullet Gun shot wounds Gun shot residue Forensic Ballistics is divided into 3 sub-categories Internal Ballistics External Ballistics Terminal Ballistics Internal Ballistics The study of the phenomenon occurring inside a firearm when a shot is fired. It includes the study of various firearm mechanisms and barrel manufacturing techniques; factors influencing internal gas pressure; and firearm recoil . The most common types of Internal Ballistics examinations are: ✓ examining mechanism to determine the causes of accidental discharge ✓ examining home-made devices (zip-guns) to determine if they are capable of discharging ammunition effectively ✓ microscopic examination and comparison of fired bullets and cartridge cases to determine whether a particular firearm was used External Ballistics The study of the projectile’s flight from the moment it leaves the muzzle of the barrel until it strikes the target. The Two most common types of External Ballistics examinations are: calculation and reconstruction of bullet trajectories establishing the maximum range of a given bullet Terminal Ballistics The study of the projectile’s effect on the target or the counter-effect of the target on the projectile.
    [Show full text]
  • How to Make Gun Powder the Old Fashioned Way in Less Than 30 Minutes - Ask a Prepper
    10/8/2019 How To Make Gun Powder The Old Fashioned Way in Less Than 30 Minutes - Ask a Prepper DIY Terms of Use Privacy Policy Ask a Prepper Search something.. Survival / Prepping Solutions My Instagram Feed Demo Facebook Demo HOME ALL ARTICLES EDITOR’S PICK SURVIVAL KNOWLEDGE HOW TO’S GUEST POSTS CONTACT ABOUT CLAUDE DAVIS Social media How To Make Gun Powder The Old Fashioned Way in Less Than 30 Minutes Share this article By James Walton Print this article Send e-mail December 30, 2016 14:33 FOLLOW US PREPPER RECOMMENDS IF YOU SEE THIS PLANT IN YOUR BACKYARD BURN IT IMMEDIATELY ENGINEERS CALL THIS “THE SOLAR PANEL KILLER” THIS BUG WILL KILL MOST by James Walton AMERICANS DURING THE NEXT CRISIS Would you believe that this powerful propellant, that has changed the world as we know it, was made as far back as 142 AD? 22LBS GONE IN 13 DAYS WITH THIS STRANGE “CARB-PAIRING” With that knowledge, how about the fact that it took nearly 1200 years for us to TRICK figure out how to use this technology in a gun. The history of this astounding 12X MORE EFFICIENT THAN substance is one that is inextricably tied to the human race. Imagine the great SOLAR PANELS? NEW battles and wars tied to this simple mixture of sulfur, carbon and potassium nitrate. INVENTION TAKES Mixed in the right ratios this mix becomes gunpowder. GREEK RITUAL REVERSES In this article, we are going to talk about the process of making gunpowder. DIABETES. DO THIS BEFORE BED! We have just become such a dependent bunch that the process, to most of us, seems like some type of magic that only a Merlin could conjure up.
    [Show full text]
  • Owner's Manual
    User’s guide for: MUZZLELOADING FIREARMS Official Sponsor ATTENTION: BEFORE REMOVING THE FIREARM FROM ITS PACKAGE READ & UNDERSTAND WARNINGS AND FULL INSTRUCTIONS AND PRECAUTIONS IN THIS OWNER’S MANUAL Owner’s Manual – MUZZLE LOADING FIREARMS CHIAPPA FIREARMS Chiappa Firearms is the brand new trade mark representing the arms manufacturers group of the Chiappa’s Family (founders of Armi Sport in far 1958) that reunite two brands leaders in their fields: ARMI SPORT: Producing perfectly working replicas of muzzle loading and breech loading firearms, with a complete and appreciated product line from American Independence War models to the mythical Lever Action rifles of epic Western era. KIMAR: Producing blank firing and signal pistol, air guns and defence guns. The two brands attend the internat ional markets from many years, especially Armi Sport that is knew by most exigent shooters, collectors and by the most important shooting and historical associations from all over the world, for the reliability, th e safety, the fidelity to the original models, the artisan finishing accuracy and the optimum quality price report of all their models. From the beginning of 2007 the Group gave an official mark to the own presence on the American market founding the CHIAPPA FIREARMS Ltd, with a convenient location in Dayton (Ohio) can provide better assistance to the distributors of Armi Sport and Kimar products throughout the USA . So CHIAPPA FIREARMS will be the brand new logo for the distribution and the guarantee protection of Armi Sport and Kimar products in the world and it’ll warrant the flexibility production and the research applied to the technical resource that have permitted in the last years the constant and continuing expansion of the group.
    [Show full text]
  • Voting from the Rooftops
    VOTING FROM THE ROOFTOPS How the Gun Industry Armed Osama bin Laden, other Foreign and Domestic Terrorists, and Common Criminals with 50 Caliber Sniper Rifles Violence Policy Center The Violence Policy Center is a national non-profit educational organization that conducts research and public education on firearms violence and provides information and analysis to policymakers, journalists, grassroots advocates, and the general public. The Center examines the role of firearms in America, analyzes trends and patterns in firearms violence, and works to develop policies to reduce gun- related death and injury. This study was authored by VPC Senior Policy Analyst Tom Diaz. This study was funded with the support of The David Bohnett Foundation, The Center on Crime, Communities & Culture of the Open Society Institute/Funders’ Collaborative for Gun Violence Prevention, The George Gund Foundation, The Joyce Foundation, and The John D. and Catherine T. MacArthur Foundation. Past studies released by the Violence Policy Center include: • Shot Full of Holes: Deconstructing John Ashcroft’s Second Amendment (July 2001) • Hispanics and Firearms Violence (May 2001) • Poisonous Pastime: The Health Risks of Target Ranges and Lead to Children, Families, and the Environment (May 2001) • Where’d They Get Their Guns?—An Analysis of the Firearms Used in High-Profile Shootings, 1963 to 2001 (April 2001) • Every Handgun Is Aimed at You: The Case for Banning Handguns (March 2001) • From Gun Games to Gun Stores: Why the Firearms Industry Wants Their Video Games on
    [Show full text]
  • 219 Zipper [PDF]
    219 ZIPPER .365 12° .253 .506 .422 .252 .063 1.359 1.621 1.938 219 ZIPPER RIFLE: . F.N. Mauser Custom BULLET DIAMETER:. 0.224" BARREL: . 27", 1 in 14" Twist MAXIMUM C.O.L.: . 2.260" CASE: . Remington MAX. CASE LENGTH: . 1.938" PRIMER: . Federal 210 CASE TRIM LENGTH: . 1.928" Winchester introduced the 219 Zipper in 1937, seven years after the Hornet and two years after the powerful 220 Swift. Chambered in the fi rm’s Model 64 lever action varmint version of the famous Model 94, it never delivered the tack-driving accuracy customers demanded and consequently never became widely popular. Winchester discontinued manufacturing the Model 64 after WW II and the 219 Zipper became an orphan in 1961 when Marlin stopped chambering its Model 336 for the cartridge. The Zipper is now completely a handloading proposition since both Remington and Winchester have discontinued producing ammunition. A necked down 25-35 WCF (which can also be formed from 30-30 brass), the 219 Zipper was and is a respectable performer. Top velocities possible for the cartridge are only 100 fps lower than those which can be developed in the 224 Weatherby Varmintmaster. The Hornady 53 grain V-MAX™ or the 55 grain Spire Point are fi ne choices for the 219 Zipper and the cartridge is large enough to propel the wind-bucking 60 grain SP or HP up to an impressive 3300 fps. H 4895 is a very good powder throughout the entire range of available bullet weights and especially with the heavier selections. Hornady 22 caliber V-MAX™ bullets are extra potent in the Zipper.
    [Show full text]
  • Rimfire Firing-Pin Indent Copper Crusher (Part 1)
    NONFERROUSNONFERROUS HEATHEAT TREATING TREATING Rimfire Firing-Pin Indent Copper Crusher (part 1) Daniel H. Herring – The HERRING GROUP, Inc.; Elmhurst, Ill. The Sporting Arms and Ammunition Manufacturers’ Institute Inc., also known as SAAMI, is an association of the nation’s leading manufacturers of rearms, ammunition and components. SAAMI is the American National Standards Institute-accredited standards Fig. 1. Firing-pin indent copper crushers developer for the commercial small arms and ammunition industry. SAAMI was for 22-caliber rimfire ammunition founded in 1926 at the request of the federal government and tasked with: creating and (courtesy of Cox Manufacturing and publishing industry standards for safety, interchangeability, reliability and quality; and Kirby & Associates) coordinating technical data to promote safe and responsible rearms use. he story of SAAMI’s rimfire firing-pin indent copper pressures and increased bullet velocities. crusher describes the reinvention of one of the most The primary advantage of rimfire ammunition is low cost, important tools in the ammunition and firearms industry typically one-fourth that of center fire. It is less expensive to T(Fig. 1). This article explains the purpose and operation manufacture a thin-walled casing with an integral-rimmed of the rimfire firing-pin indent copper crusher and how an primer than it is to seat a separate primer in the center of the unusual chain of events almost led to the disappearance of this head of the casing. simple but important technology. The most common rimfire ammunition is the 22LR (22-caliber long rif le). It is considered the most popular round Rimfire Ammunition in the world and is commonly used for target shooting, small- In order to discuss the rimfire copper crusher, we need to take a game hunting, competitive rifle shooting and, to a lesser extent, step back and first explain what rimfire ammunition is and how it works.
    [Show full text]
  • Offensive Weapons Bill Written Evidence Submitted by Simon Edwards Section 28 Conclusion
    Offensive Weapons Bill Written evidence submitted by Simon Edwards Section 28 Proposal to move rifles that can discharge a shot bullet or other missile with kinetic energy of more than 13,600 joules at the muzzle of the weapon to section 5 of the Firearms Act 1968; this amounts to a prohibition of these firearms. In her summing, up Victoria Atkins stated that in one example she was given it was stated that the rifles are large and heavy and were capable of shooting the distance between London Bridge and Trafalgar Square – some 3500 meters. Victoria also stated that there had been a recent increase in seizures at the UK border of higher power weaponry and ordinance, which were assessed to be destined for the criminal marketplace, and that the criminal marketplace is showing a growing demand for more powerful weaponry. 1) Can a rifle with 13,600 joules of Muzzle Energy shoot 3500 meters? The answer is yes but I believe that Victoria Atkins has been misleading in the way she used this information. a. There is a vast difference between an aimed shot at a target and the distance a bullet will travel. At a recent long-range shooting event where 62 of the world’s best target shooters assembled less than one third of the shooters were able to hit a 1m wide target and 1728 meters within 3 shots. An accurate 3500-meter shot is simply not realistic, outside being one of the world’s best shooters supported by extremely expensive instruments and custom-made ammunition.
    [Show full text]
  • Ballistic Aiming System Manual
    BALLISTICS AIMING SYSTEM Table of Contents Boone and Crockett™ Big Game Reticle ......................... Page 1 Varmint Hunter’s™ Reticle .................................... Page 11 LR Duplex® Reticle .......................................... Page 22 LRV Duplex® Reticle ......................................... Page 29 SAbot Ballistics Reticle (SA.B.R.®) ............................. Page 34 Ballistic FireDot® Reticle ..................................... Page 44 Multi-FireDot™ Reticle....................................... Page 51 Pig-Plex Ballistic Reticle...................................... Page 59 TMOA™ Reticles ............................................ Page 64 Various language translations of the BAS Manual can be found at www.leupold.com. La traduction en français du manuel BAS se trouve à www.leupold.com. La traducción al español del manual BAS se encuentra en www.leupold.com. Das BAS-Handbuch in deutscher Sprache finden Sie unter www.leupold.com. La traduzione in italiano del manuale BAS è pubblicata sul sito seguente: www.leupold.com. 1 The Leupold Ballistics Aiming System®– Boone and Crockett™ Big Game Reticle The goal of every hunter is a successful hunt with a clean harvest. It was with this in mind that Leupold® created the Leupold Ballistics Aiming System®. Because we so strongly agree with the Boone and Crockett Club’s legacy of wildlife conservation and ethical fair chase hunting, we have designated one of the system’s reticles as the Boone and Crockett™ Big Game reticle. The Boone and Crockett Big Game reticle gives the hunter very useful tools intended to bring about successful hunts with clean and efficient harvests. Through the use of these straightforward and easy-to-follow instructions, it is sincerely hoped that all hunters will find their skills improved and their hunts more successful. Boone and Crockett Club® is a registered trademark of the Boone and Crockett Club, and is used with their expressed written permission.
    [Show full text]
  • Artillery Through the Ages, by Albert Manucy 1
    Artillery Through the Ages, by Albert Manucy 1 Artillery Through the Ages, by Albert Manucy The Project Gutenberg EBook of Artillery Through the Ages, by Albert Manucy This eBook is for the use of anyone anywhere at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org Title: Artillery Through the Ages A Short Illustrated History of Cannon, Emphasizing Types Used in America Author: Albert Manucy Release Date: January 30, 2007 [EBook #20483] Language: English Artillery Through the Ages, by Albert Manucy 2 Character set encoding: ISO-8859-1 *** START OF THIS PROJECT GUTENBERG EBOOK ARTILLERY THROUGH THE AGES *** Produced by Juliet Sutherland, Christine P. Travers and the Online Distributed Proofreading Team at http://www.pgdp.net ARTILLERY THROUGH THE AGES A Short Illustrated History of Cannon, Emphasizing Types Used in America UNITED STATES DEPARTMENT OF THE INTERIOR Fred A. Seaton, Secretary NATIONAL PARK SERVICE Conrad L. Wirth, Director For sale by the Superintendent of Documents U. S. Government Printing Office Washington 25, D. C. -- Price 35 cents (Cover) FRENCH 12-POUNDER FIELD GUN (1700-1750) ARTILLERY THROUGH THE AGES A Short Illustrated History of Cannon, Emphasizing Types Used in America Artillery Through the Ages, by Albert Manucy 3 by ALBERT MANUCY Historian Southeastern National Monuments Drawings by Author Technical Review by Harold L. Peterson National Park Service Interpretive Series History No. 3 UNITED STATES GOVERNMENT PRINTING OFFICE WASHINGTON: 1949 (Reprint 1956) Many of the types of cannon described in this booklet may be seen in areas of the National Park System throughout the country.
    [Show full text]
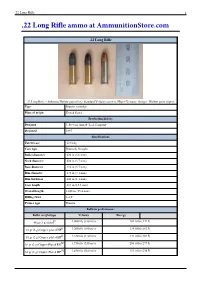
  • 22 Long Rifle Ammo at Ammunitionstore.Com
    .22 Long Rifle 1 .22 Long Rifle ammo at AmmunitionStore.com .22 Long Rifle .22 Long Rifle – Subsonic Hollow point (left). Standard Velocity (center), Hyper-Velocity "Stinger" Hollow point (right). Type Rimfire cartridge Place of origin United States Production history Designer J. Stevens Arm & Tool Company Designed 1887 Specifications Parent case .22 Long Case type Rimmed, Straight Bullet diameter .222 in (5.6 mm) Neck diameter .226 in (5.7 mm) Base diameter .226 in (5.7 mm) Rim diameter .278 in (7.1 mm) Rim thickness .043 in (1.1 mm) Case length .613 in (15.6 mm) Overall length 1.000 in (25.4 mm) Rifling twist 1–16" Primer type Rimfire Ballistic performance Bullet weight/type Velocity Energy [] 40 gr (3 g) Solid 1,080 ft/s (330 m/s) 104 ft·lbf (141 J) [] 38 gr (2 g) Copper-plated HP 1,260 ft/s (380 m/s) 134 ft·lbf (182 J) [] 31 gr (2 g) Copper-plated HP 1,430 ft/s (440 m/s) 141 ft·lbf (191 J) [1] 30 gr (2 g) Copper-Plated RN 1,750 ft/s (530 m/s) 204 ft·lbf (277 J) [1] 32 gr (2 g) Copper-Plated HP 1,640 ft/s (500 m/s) 191 ft·lbf (259 J) .22 Long Rifle 2 [][1] Source(s): The .22 Long Rifle rimfire (5.6×15R – metric designation) cartridge is a long established variety of ammunition, and in terms of units sold is still by far the most common in the world today. The cartridge is often referred to simply as .22 LR ("twenty-two-/ˈɛl/-/ˈɑr/") and various rifles, pistols, revolvers, and even some smoothbore shotguns have been manufactured in this caliber.
    [Show full text]