DOCSLIB.ORG

1 Space Curves and Tangent Lines 2 Gradients and Tangent Planes

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
1 Space Curves and Tangent Lines 2 Gradients and Tangent Planes CLASS NOTES for CHAPTER 4, Nonlinear Programming 1 Space Curves and Tangent Lines Recall that space curves are de¯ned by a set of parametric equations, x1(t) 2 x2(t) 3 r(t) = . 6 . 7 6 7 6 xn(t) 7 4 5 In Calc III, we might have written this a little di®erently, ~r(t) =< x(t); y(t); z(t) > but here we want to use n dimensions rather than two or three dimensions. The derivative and antiderivative of r with respect to t is done component- wise, x10 (t) x1(t) dt 2 x20 (t) 3 2 R x2(t) dt 3 r(t) = . ; R(t) = . 6 . 7 6 R . 7 6 7 6 7 6 xn0 (t) 7 6 xn(t) dt 7 4 5 4 5 And the local linear approximation to r(t) is alsoRdone componentwise. The tangent line (in n dimensions) can be written easily- the derivative at t = a is the direction of the curve, so the tangent line is given by: x1(a) x10 (a) 2 x2(a) 3 2 x20 (a) 3 L(t) = . + t . 6 . 7 6 . 7 6 7 6 7 6 xn(a) 7 6 xn0 (a) 7 4 5 4 5 In Class Exercise: Use Maple to plot the curve r(t) = [cos(t); sin(t); t]T ¼ and its tangent line at t = 2 . 2 Gradients and Tangent Planes Let f : Rn R. In this case, we can write: ! y = f(x1; x2; x3; : : : ; xn) 1 Note that any function that we wish to optimize must be of this form- It would not make sense to ¯nd the maximum of a function like a space curve; n dimensional coordinates are not well-ordered like the real line- so the fol- lowing statement would be meaningless: (3; 5) > (1; 2). This type of function is sometimes called a surface even though we can't graph it if the domain has a higher dimension than 2. The gradient of f, f, is de¯ned by its partial derivatives. We will denote @f r @xi as fxi , and so: fx1 (x1; x2; : : : ; xn) 2 fx2 (x1; x2; : : : ; xn) 3 f(x1; x2; : : : ; xn) = . r 6 . 7 6 7 6 fxn (x1; x2; : : : ; xn) 7 4 5 NOTE: When writing the gradient, we will not distinguish between it being a row vector or a column vector. For some ideas, it may be more clear notationally to write it as a column, but for computations, it is a row vector. Normally, it will be clear from the context whether it is a row or column. The rate of change of f at x = a in the direction of the unit vector u is de¯ned as the directional derivative of f: Duf(a) = f(a) u r ¢ If we recall the useful relationship between any two vectors u, v Rn, 2 u v = u 2 v 2 cos(θ) ¢ k k k k then we see that the direction for which the rate of change of f is a maximum is in the direction of f(a). In Class Example:rFind the maximum rate of change of f at the given point and the direction in which it occurs: f(x; y) = x + y=z at (4; 3). The linearization of f at x = a is the tangent plane, L(x) = f(a) + f(a) (x a) r ¢ ¡ which is also the ¯rst order Taylor series approximation to f at a. 2 2.1 Surfaces and Contours In maximizing or minimizing a function, we'll consider equations like: F (x) = k, where k is a real number. From our earlier discussion on the Implicit Function Theorem, we know that this equation could implicitly de¯ne one of the variables in terms of the others. In Calculus III, for example, we saw F (x; y) = k de¯nes a level curve in the plane. ² F (x; y; z) = k de¯nes a level surface in three dimensions. ² Now let r(t) be a curve on the surface de¯ned by F (x) = k. Then we could write F as dependent on t, and di®erentiate with respect to t: F (r(t)) r0(t) = 0 r ¢ which implies that the gradient is orthogonal to any curve on the surface. In particular, we can compute the tangent line or plane at the point (a; b) or (a; b; c): Fx(a; b) (x a) + Fy(a; b) (y b) = 0 ² ¢ ¡ ¢ ¡ Fx(a; b; c) (x a) + Fy(a; b; c) (y b) + Fz(a; b; c) (z c) = 0 ² ¢ ¡ ¢ ¡ ¢ ¡ If x Rn, this can be written compactly as F (a) (x a) = 0 2 r ¢ ¡ In Class Example: Compute the tangent line and show that the gradient 2 2 1 1 is orthogonal to it, if x + y = 1 at p2 ; p2 . In this case, the gradient of ³ ´ F (x; y) = x2 + y2 is [2x; 2y], and at the given point, the gradient is [p2; p2]. Notice that this vector points directly opposite from the center of the circle. On the other hand, the equation of the tangent line is: 1 1 p2 x + p2 y = 0 µ ¡ p2¶ µ ¡ p2¶ or in the more familiar form, y = x + p2. The \slope" of the gradient is 1, while the slope of the tangent line¡is 1. In two dimensions such as this, a ¡ F line in the direction of the gradient would have slope y , while the slope of Fx F the tangent line would be x . ¡Fy The important point in this section: Given a level surface of the form F (x) = k, the gradient F at x = a is orthogonal. Furthermore, the gradient points in the directionr where F increases the fastest (for y = F (x). 3 3 Derivatives we don't see in Calculus III 3.1 The Hessian Matrix n Let f : R R, so that we have something in the form of y = f(x1; x2; : : : ; xn). We have already! seen that the derivative of f takes the form of the gradient. We now examine the second derivative of f, and we'll see that the second derivative forms what is called the Hessian matrix. The ¯rst derivative is in the form of the gradient, where we have a vector of functions. Let fxi (x1; x2; : : : ; xn) = gi(x1; x2; : : : ; xn). Now each function g is also a function from Rn to R, and so the derivative of g is also a gradient. We could therefore write the second derivative of f in matrix form to obtain what is called the Hessian of f: g1 fx1x1 fx1x2 : : : fx1xn r 2 g2 3 2 fx2x1 fx2x2 : : : fx2xn 3 Hf = r. = . 6 . 7 6 . 7 6 7 6 7 6 gn 7 6 fxnx1 fxnx2 : : : fxnxn 7 4 r 5 4 5 In Class Example: Let f(x; y) = x3 +2xy y2. Compute the gradient and Hessian of f. ¡ 3x2 + 2y 6x + 2 2 f = ; Hf = r · 2x 2y ¸ · 2 2 ¸ ¡ ¡ You might note that, if the second partials of f are continuous, then Hf will always be a symmetric matrix (this is a consequence of Clairaut's Theorem). In Class Example: Let f(x; y) = 2 + x2 + x + xy + y + y2. Show that f can be written as: 1 f(a) + f(a)(x a) + (x a)T Hf(a)(x a) r ¡ 2 ¡ ¡ where a = (0; 0). First, we compute f and Hf: r 2x + 1 + y 2 1 f = ; Hf = r · x + 1 + 2y ¸ · 1 2 ¸ 4 Substituting (x; y) = (0; 0), the gradient is [1; 1], and now compute: x 0 1 2 1 x 0 2 + [1; 1] ¡ + [x 0; y 0] ¡ ¢ · y 0 ¸ 2 ¡ ¡ · 1 2 ¸ · y 0 ¸ ¡ ¡ 1 2x + y 2 + x + y + [x; y] = 2 + x + y + x2 + xy + y2 2 · x + 2y ¸ The Second Order Taylor Approximation If f : Rn R, then the Taylor approximation to f at a to second order is: ! 1 f(x) f(a) + f(a)(x a) + (x a)T Hf(a)(x a) ¼ r ¡ 2 ¡ ¡ 3.2 Connecting the Hessian to Calculus III In Calc III, when we were ¯nding local extrema, we had the \Second Deriva- tives Test". To generalize this result requires a little linear algebra, but the end result is that if x = a is a critical point of f, and Hf(a) has all positive eigenvalues, then f has a local minimum at a. If Hf(a) has all negative eigenvalues, then f has a local maximum at a. If the eigenvalues are mixed in sign, there is a saddle point. 3.3 The Jacobian Matrix Let f : Rn Rm. The we could write f using m coordinate functions, each depending !on n variables, f1(x1; : : : ; xn) 2 f2(x1; : : : ; xn) 3 f(x1; : : : ; xn) = . 6 . 7 6 7 6 fm(x1; : : : ; xn) 7 4 5 De¯nition: The derivative of f takes the form of a matrix called the Jaco- bian of f, constructed by taking the partial derivatives: (f1)x1 (f1)x2 (f1)xn ¢ ¢ ¢ 2 (f2)x1 (f2)x2 (f2)xn 3 Jf = . ¢ ¢ ¢ . 6 . 7 6 7 6 (fm)x1 (fm)x2 (fm)xn 7 4 ¢ ¢ ¢ 5 5 In Class Example: Compute the Jacobian of: x2 + yz + z f(x; y; z) = 2 y2 + xy + 3 3 sin(xyz) 4 5 2x z y + 1 Jf = 2 y 2y + x 0 3 yz cos(xyz) xz cos(xyz) xy cos(xyz) 4 5 If f : Rn Rm, then the linearization of f at x = a is given by: ! L(x) = f(a) + Jf(a)(x a) ¡ 4 The Extreme Value Theorem Let f : Rn R be continuous on a closed and bounded domain D.
Load more

Recommended publications
  • Infinitesimal and Tangent to Polylogarithmic Complexes For
    AIMS Mathematics, 4(4): 1248–1257. DOI:10.3934/math.2019.4.1248 Received: 11 June 2019 Accepted: 11 August 2019 http://www.aimspress.com/journal/Math Published: 02 September 2019 Research article Infinitesimal and tangent to polylogarithmic complexes for higher weight Raziuddin Siddiqui* Department of Mathematical Sciences, Institute of Business Administration, Karachi, Pakistan * Correspondence: Email: [email protected]; Tel: +92-213-810-4700 Abstract: Motivic and polylogarithmic complexes have deep connections with K-theory. This article gives morphisms (different from Goncharov’s generalized maps) between |-vector spaces of Cathelineau’s infinitesimal complex for weight n. Our morphisms guarantee that the sequence of infinitesimal polylogs is a complex. We are also introducing a variant of Cathelineau’s complex with the derivation map for higher weight n and suggesting the definition of tangent group TBn(|). These tangent groups develop the tangent to Goncharov’s complex for weight n. Keywords: polylogarithm; infinitesimal complex; five term relation; tangent complex Mathematics Subject Classification: 11G55, 19D, 18G 1. Introduction The classical polylogarithms represented by Lin are one valued functions on a complex plane (see [11]). They are called generalization of natural logarithms, which can be represented by an infinite series (power series): X1 zk Li (z) = = − ln(1 − z) 1 k k=1 X1 zk Li (z) = 2 k2 k=1 : : X1 zk Li (z) = for z 2 ¼; jzj < 1 n kn k=1 The other versions of polylogarithms are Infinitesimal (see [8]) and Tangential (see [9]). We will discuss group theoretic form of infinitesimal and tangential polylogarithms in x 2.3, 2.4 and 2.5 below.
    [Show full text]
  • The Matrix Calculus You Need for Deep Learning
    The Matrix Calculus You Need For Deep Learning Terence Parr and Jeremy Howard July 3, 2018 (We teach in University of San Francisco's MS in Data Science program and have other nefarious projects underway. You might know Terence as the creator of the ANTLR parser generator. For more material, see Jeremy's fast.ai courses and University of San Francisco's Data Institute in- person version of the deep learning course.) HTML version (The PDF and HTML were generated from markup using bookish) Abstract This paper is an attempt to explain all the matrix calculus you need in order to understand the training of deep neural networks. We assume no math knowledge beyond what you learned in calculus 1, and provide links to help you refresh the necessary math where needed. Note that you do not need to understand this material before you start learning to train and use deep learning in practice; rather, this material is for those who are already familiar with the basics of neural networks, and wish to deepen their understanding of the underlying math. Don't worry if you get stuck at some point along the way|just go back and reread the previous section, and try writing down and working through some examples. And if you're still stuck, we're happy to answer your questions in the Theory category at forums.fast.ai. Note: There is a reference section at the end of the paper summarizing all the key matrix calculus rules and terminology discussed here. arXiv:1802.01528v3 [cs.LG] 2 Jul 2018 1 Contents 1 Introduction 3 2 Review: Scalar derivative rules4 3 Introduction to vector calculus and partial derivatives5 4 Matrix calculus 6 4.1 Generalization of the Jacobian .
    [Show full text]
  • 2. the Tangent Line
    2. The Tangent Line The tangent line to a circle at a point P on its circumference is the line perpendicular to the radius of the circle at P. In Figure 1, The line T is the tangent line which is Tangent Line perpendicular to the radius of the circle at the point P. T Figure 1: A Tangent Line to a Circle While the tangent line to a circle has the property that it is perpendicular to the radius at the point of tangency, it is not this property which generalizes to other curves. We shall make an observation about the tangent line to the circle which is carried over to other curves, and may be used as its defining property. Let us look at a specific example. Let the equation of the circle in Figure 1 be x22 + y = 25. We may easily determine the equation of the tangent line to this circle at the point P(3,4). First, we observe that the radius is a segment of the line passing through the origin (0, 0) and P(3,4), and its equation is (why?). Since the tangent line is perpendicular to this line, its slope is -3/4 and passes through P(3, 4), using the point-slope formula, its equation is found to be Let us compute y-values on both the tangent line and the circle for x-values near the point P(3, 4). Note that near P, we can solve for the y-value on the upper half of the circle which is found to be When x = 3.01, we find the y-value on the tangent line is y = -3/4(3.01) + 25/4 = 3.9925, while the corresponding value on the circle is (Note that the tangent line lie above the circle, so its y-value was expected to be a larger.) In Table 1, we indicate other corresponding values as we vary x near P.
    [Show full text]
  • A Brief Tour of Vector Calculus
    A BRIEF TOUR OF VECTOR CALCULUS A. HAVENS Contents 0 Prelude ii 1 Directional Derivatives, the Gradient and the Del Operator 1 1.1 Conceptual Review: Directional Derivatives and the Gradient........... 1 1.2 The Gradient as a Vector Field............................ 5 1.3 The Gradient Flow and Critical Points ....................... 10 1.4 The Del Operator and the Gradient in Other Coordinates*............ 17 1.5 Problems........................................ 21 2 Vector Fields in Low Dimensions 26 2 3 2.1 General Vector Fields in Domains of R and R . 26 2.2 Flows and Integral Curves .............................. 31 2.3 Conservative Vector Fields and Potentials...................... 32 2.4 Vector Fields from Frames*.............................. 37 2.5 Divergence, Curl, Jacobians, and the Laplacian................... 41 2.6 Parametrized Surfaces and Coordinate Vector Fields*............... 48 2.7 Tangent Vectors, Normal Vectors, and Orientations*................ 52 2.8 Problems........................................ 58 3 Line Integrals 66 3.1 Defining Scalar Line Integrals............................. 66 3.2 Line Integrals in Vector Fields ............................ 75 3.3 Work in a Force Field................................. 78 3.4 The Fundamental Theorem of Line Integrals .................... 79 3.5 Motion in Conservative Force Fields Conserves Energy .............. 81 3.6 Path Independence and Corollaries of the Fundamental Theorem......... 82 3.7 Green's Theorem.................................... 84 3.8 Problems........................................ 89 4 Surface Integrals, Flux, and Fundamental Theorems 93 4.1 Surface Integrals of Scalar Fields........................... 93 4.2 Flux........................................... 96 4.3 The Gradient, Divergence, and Curl Operators Via Limits* . 103 4.4 The Stokes-Kelvin Theorem..............................108 4.5 The Divergence Theorem ...............................112 4.6 Problems........................................114 List of Figures 117 i 11/14/19 Multivariate Calculus: Vector Calculus Havens 0.
    [Show full text]
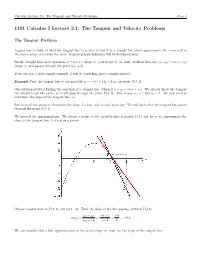
  • 1101 Calculus I Lecture 2.1: the Tangent and Velocity Problems
    Calculus Lecture 2.1: The Tangent and Velocity Problems Page 1 1101 Calculus I Lecture 2.1: The Tangent and Velocity Problems The Tangent Problem A good way to think of what the tangent line to a curve is that it is a straight line which approximates the curve well in the region where it touches the curve. A more precise definition will be developed later. Recall, straight lines have equations y = mx + b (slope m, y-intercept b), or, more useful in this case, y − y0 = m(x − x0) (slope m, and passes through the point (x0, y0)). Your text has a fairly simple example. I will do something more complex instead. Example Find the tangent line to the parabola y = −3x2 + 12x − 8 at the point P (3, 1). Our solution involves finding the equation of a straight line, which is y − y0 = m(x − x0). We already know the tangent line should touch the curve, so it will pass through the point P (3, 1). This means x0 = 3 and y0 = 1. We now need to determine the slope of the tangent line, m. But we need two points to determine the slope of a line, and we only know one. We only know that the tangent line passes through the point P (3, 1). We proceed by approximations. We choose a point on the parabola that is nearby (3,1) and use it to approximate the slope of the tangent line. Let’s draw a sketch. Choose a point close to P (3, 1), say Q(4, −8).
    [Show full text]
  • Policy Gradient
    Lecture 7: Policy Gradient Lecture 7: Policy Gradient David Silver Lecture 7: Policy Gradient Outline 1 Introduction 2 Finite Difference Policy Gradient 3 Monte-Carlo Policy Gradient 4 Actor-Critic Policy Gradient Lecture 7: Policy Gradient Introduction Policy-Based Reinforcement Learning In the last lecture we approximated the value or action-value function using parameters θ, V (s) V π(s) θ ≈ Q (s; a) Qπ(s; a) θ ≈ A policy was generated directly from the value function e.g. using -greedy In this lecture we will directly parametrise the policy πθ(s; a) = P [a s; θ] j We will focus again on model-free reinforcement learning Lecture 7: Policy Gradient Introduction Value-Based and Policy-Based RL Value Based Learnt Value Function Implicit policy Value Function Policy (e.g. -greedy) Policy Based Value-Based Actor Policy-Based No Value Function Critic Learnt Policy Actor-Critic Learnt Value Function Learnt Policy Lecture 7: Policy Gradient Introduction Advantages of Policy-Based RL Advantages: Better convergence properties Effective in high-dimensional or continuous action spaces Can learn stochastic policies Disadvantages: Typically converge to a local rather than global optimum Evaluating a policy is typically inefficient and high variance Lecture 7: Policy Gradient Introduction Rock-Paper-Scissors Example Example: Rock-Paper-Scissors Two-player game of rock-paper-scissors Scissors beats paper Rock beats scissors Paper beats rock Consider policies for iterated rock-paper-scissors A deterministic policy is easily exploited A uniform random policy
    [Show full text]
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]
  • High Order Gradient, Curl and Divergence Conforming Spaces, with an Application to NURBS-Based Isogeometric Analysis
    High order gradient, curl and divergence conforming spaces, with an application to compatible NURBS-based IsoGeometric Analysis R.R. Hiemstraa, R.H.M. Huijsmansa, M.I.Gerritsmab aDepartment of Marine Technology, Mekelweg 2, 2628CD Delft bDepartment of Aerospace Technology, Kluyverweg 2, 2629HT Delft Abstract Conservation laws, in for example, electromagnetism, solid and fluid mechanics, allow an exact discrete representation in terms of line, surface and volume integrals. We develop high order interpolants, from any basis that is a partition of unity, that satisfy these integral relations exactly, at cell level. The resulting gradient, curl and divergence conforming spaces have the propertythat the conservationlaws become completely independent of the basis functions. This means that the conservation laws are exactly satisfied even on curved meshes. As an example, we develop high ordergradient, curl and divergence conforming spaces from NURBS - non uniform rational B-splines - and thereby generalize the compatible spaces of B-splines developed in [1]. We give several examples of 2D Stokes flow calculations which result, amongst others, in a point wise divergence free velocity field. Keywords: Compatible numerical methods, Mixed methods, NURBS, IsoGeometric Analyis Be careful of the naive view that a physical law is a mathematical relation between previously defined quantities. The situation is, rather, that a certain mathematical structure represents a given physical structure. Burke [2] 1. Introduction In deriving mathematical models for physical theories, we frequently start with analysis on finite dimensional geometric objects, like a control volume and its bounding surfaces. We assign global, ’measurable’, quantities to these different geometric objects and set up balance statements.
    [Show full text]
  • Calculus Formulas and Theorems
    Formulas and Theorems for Reference I. Tbigonometric Formulas l. sin2d+c,cis2d:1 sec2d l*cot20:<:sc:20 +.I sin(-d) : -sitt0 t,rs(-//) = t r1sl/ : -tallH 7. sin(A* B) :sitrAcosB*silBcosA 8. : siri A cos B - siu B <:os,;l 9. cos(A+ B) - cos,4cos B - siuA siriB 10. cos(A- B) : cosA cosB + silrA sirrB 11. 2 sirrd t:osd 12. <'os20- coS2(i - siu20 : 2<'os2o - I - 1 - 2sin20 I 13. tan d : <.rft0 (:ost/ I 14. <:ol0 : sirrd tattH 1 15. (:OS I/ 1 16. cscd - ri" 6i /F tl r(. cos[I ^ -el : sitt d \l 18. -01 : COSA 215 216 Formulas and Theorems II. Differentiation Formulas !(r") - trr:"-1 Q,:I' ]tra-fg'+gf' gJ'-,f g' - * (i) ,l' ,I - (tt(.r))9'(.,') ,i;.[tyt.rt) l'' d, \ (sttt rrJ .* ('oqI' .7, tJ, \ . ./ stll lr dr. l('os J { 1a,,,t,:r) - .,' o.t "11'2 1(<,ot.r') - (,.(,2.r' Q:T rl , (sc'c:.r'J: sPl'.r tall 11 ,7, d, - (<:s<t.r,; - (ls(].]'(rot;.r fr("'),t -.'' ,1 - fr(u") o,'ltrc ,l ,, 1 ' tlll ri - (l.t' .f d,^ --: I -iAl'CSllLl'l t!.r' J1 - rz 1(Arcsi' r) : oT Il12 Formulas and Theorems 2I7 III. Integration Formulas 1. ,f "or:artC 2. [\0,-trrlrl *(' .t "r 3. [,' ,t.,: r^x| (' ,I 4. In' a,,: lL , ,' .l 111Q 5. In., a.r: .rhr.r' .r r (' ,l f 6. sirr.r d.r' - ( os.r'-t C ./ 7. /.,,.r' dr : sitr.i'| (' .t 8. tl:r:hr sec,rl+ C or ln Jccrsrl+ C ,f'r^rr f 9.
    [Show full text]
  • Leonhard Euler - Wikipedia, the Free Encyclopedia Page 1 of 14
    Leonhard Euler - Wikipedia, the free encyclopedia Page 1 of 14 Leonhard Euler From Wikipedia, the free encyclopedia Leonhard Euler ( German pronunciation: [l]; English Leonhard Euler approximation, "Oiler" [1] 15 April 1707 – 18 September 1783) was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion of a mathematical function.[2] He is also renowned for his work in mechanics, fluid dynamics, optics, and astronomy. Euler spent most of his adult life in St. Petersburg, Russia, and in Berlin, Prussia. He is considered to be the preeminent mathematician of the 18th century, and one of the greatest of all time. He is also one of the most prolific mathematicians ever; his collected works fill 60–80 quarto volumes. [3] A statement attributed to Pierre-Simon Laplace expresses Euler's influence on mathematics: "Read Euler, read Euler, he is our teacher in all things," which has also been translated as "Read Portrait by Emanuel Handmann 1756(?) Euler, read Euler, he is the master of us all." [4] Born 15 April 1707 Euler was featured on the sixth series of the Swiss 10- Basel, Switzerland franc banknote and on numerous Swiss, German, and Died Russian postage stamps. The asteroid 2002 Euler was 18 September 1783 (aged 76) named in his honor. He is also commemorated by the [OS: 7 September 1783] Lutheran Church on their Calendar of Saints on 24 St. Petersburg, Russia May – he was a devout Christian (and believer in Residence Prussia, Russia biblical inerrancy) who wrote apologetics and argued Switzerland [5] forcefully against the prominent atheists of his time.
    [Show full text]
  • Integrating Gradients
    Integrating gradients 1 dimension The \gradient" of a function f(x) in one dimension (i.e., depending on only one variable) is just the derivative, f 0(x). We want to solve f 0(x) = k(x); (1) where k(x) is a known function. When we find a primitive function K(x) to k(x), the general form of f is K plus an arbitrary constant, f(x) = K(x) + C: (2) Example: With f 0(x) = 2=x we find f(x) = 2 ln x + C, where C is an undetermined constant. 2 dimensions We let the function depend on two variables, f(x; y). When the gradient rf is known, we have known functions k1 and k2 for the partial derivatives: @ f(x; y) = k (x; y); @x 1 @ f(x; y) = k (x; y): (3) @y 2 @f To solve this, we integrate one of them. To be specific, we here integrate @x over x. We find a primitive function with respect to x (thus keeping y constant) to k1 and call it k3. The general form of f will be k3 plus an arbitrary term whose x-derivative is zero. In other words, f(x; y) = k3(x; y) + B(y); (4) where B(y) is an unknown function of y. We have made some progress, because we have replaced an unknown function of two variables with another unknown function depending only on one variable. @f The best way to come further is not to integrate @y over y. That would give us a second unknown function, D(x).
    [Show full text]
  • Mean Value Theorem on Manifolds
    MEAN VALUE THEOREMS ON MANIFOLDS Lei Ni Abstract We derive several mean value formulae on manifolds, generalizing the clas- sical one for harmonic functions on Euclidean spaces as well as the results of Schoen-Yau, Michael-Simon, etc, on curved Riemannian manifolds. For the heat equation a mean value theorem with respect to `heat spheres' is proved for heat equation with respect to evolving Riemannian metrics via a space-time consideration. Some new monotonicity formulae are derived. As applications of the new local monotonicity formulae, some local regularity theorems concerning Ricci flow are proved. 1. Introduction The mean value theorem for harmonic functions plays an central role in the theory of harmonic functions. In this article we discuss its generalization on manifolds and show how such generalizations lead to various monotonicity formulae. The main focuses of this article are the corresponding results for the parabolic equations, on which there have been many works, including [Fu, Wa, FG, GL1, E1], and the application of the new monotonicity formula to the study of Ricci flow. Let us start with the Watson's mean value formula [Wa] for the heat equation. Let U be a open subset of Rn (or a Riemannian manifold). Assume that u(x; t) is 2 a C solution to the heat equation in a parabolic region UT = U £ (0;T ). For any (x; t) de¯ne the `heat ball' by 8 9 jx¡yj2 < ¡ 4(t¡s) = e ¡n E(x; t; r) := (y; s) js · t; n ¸ r : : (4¼(t ¡ s)) 2 ; Then Z 1 jx ¡ yj2 u(x; t) = n u(y; s) 2 dy ds r E(x;t;r) 4(t ¡ s) for each E(x; t; r) ½ UT .
    [Show full text]