Geometry Caching for Ray-Tracing Displacement Maps
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

AWE Surface 1.2 Documentation
AWE Surface 1.2 Documentation AWE Surface is a new, robust, highly optimized, physically plausible shader for DAZ Studio and 3Delight employing physically based rendering (PBR) metalness / roughness workflow. Using a primarily uber shader approach, it can be used to render materials such as dielectrics, glass and metal. Features Highlight Physically based BRDF (Oren Nayar for diffuse, Cook Torrance, Ashikhmin Shirley and GGX for specular). Micro facet energy loss compensation for the diffuse and transmission lobe. Transmission with Beer-Lambert based absorption. BRDF based importance sampling. Multiple importance sampling (MIS) with 3delight's path traced area light shaders such as the aweAreaPT shader. Explicit Russian Roulette for next event estimation and path termination. Raytraced subsurface scattering with forward/backward scattering via Henyey Greenstein phase function. Physically based Fresnel for both dielectric and metal materials. Unified index of refraction value for both reflection and transmission with dielectrics. An artist friendly metallic Fresnel based on Ole Gulbrandsen model using reflection color and edge tint to derive complex IOR. Physically based thin film interference (iridescence). Shader based, global illumination. Luminance based, Reinhard tone mapping with exposure, temperature and saturation controls. Toggle switches for each lobe. Diffuse Oren Nayar based translucency with support for bleed through shadows. Can use separate front/back side diffuse color and texture. Two specular/reflection lobes for the base, one specular/reflection lobe for coat. Anisotropic specular and reflection (only with Ashikhmin Shirley and GGX BRDF), with map- controllable direction. Glossy Fresnel with explicit roughness values, one for the base and one for the coat layer. Optimized opacity handling with user controllable thresholds. -

Real-Time Rendering Techniques with Hardware Tessellation
Volume 34 (2015), Number x pp. 0–24 COMPUTER GRAPHICS forum Real-time Rendering Techniques with Hardware Tessellation M. Nießner1 and B. Keinert2 and M. Fisher1 and M. Stamminger2 and C. Loop3 and H. Schäfer2 1Stanford University 2University of Erlangen-Nuremberg 3Microsoft Research Abstract Graphics hardware has been progressively optimized to render more triangles with increasingly flexible shading. For highly detailed geometry, interactive applications restricted themselves to performing transforms on fixed geometry, since they could not incur the cost required to generate and transfer smooth or displaced geometry to the GPU at render time. As a result of recent advances in graphics hardware, in particular the GPU tessellation unit, complex geometry can now be generated on-the-fly within the GPU’s rendering pipeline. This has enabled the generation and displacement of smooth parametric surfaces in real-time applications. However, many well- established approaches in offline rendering are not directly transferable due to the limited tessellation patterns or the parallel execution model of the tessellation stage. In this survey, we provide an overview of recent work and challenges in this topic by summarizing, discussing, and comparing methods for the rendering of smooth and highly-detailed surfaces in real-time. 1. Introduction Hardware tessellation has attained widespread use in computer games for displaying highly-detailed, possibly an- Graphics hardware originated with the goal of efficiently imated, objects. In the animation industry, where displaced rendering geometric surfaces. GPUs achieve high perfor- subdivision surfaces are the typical modeling and rendering mance by using a pipeline where large components are per- primitive, hardware tessellation has also been identified as a formed independently and in parallel. -

Position, Displacement, Velocity Big Picture
Position, Displacement, Velocity Big Picture I Want to know how/why things move I Need a way to describe motion mathematically: \Kinematics" I Tools of kinematics: calculus (rates) and vectors (directions) I Chapters 2, 4 are all about kinematics I First 1D, then 2D/3D I Main ideas: position, velocity, acceleration Language is crucial Physics uses ordinary words but assigns specific technical meanings! WORD ORDINARY USE PHYSICS USE position where something is where something is velocity speed speed and direction speed speed magnitude of velocity vec- tor displacement being moved difference in position \as the crow flies” from one instant to another Language, continued WORD ORDINARY USE PHYSICS USE total distance displacement or path length traveled path length trav- eled average velocity | displacement divided by time interval average speed total distance di- total distance divided by vided by time inter- time interval val How about some examples? Finer points I \instantaneous" velocity v(t) changes from instant to instant I graphically, it's a point on a v(t) curve or the slope of an x(t) curve I average velocity ~vavg is not a function of time I it's defined for an interval between instants (t1 ! t2, ti ! tf , t0 ! t, etc.) I graphically, it's the \rise over run" between two points on an x(t) curve I in 1D, vx can be called v I it's a component that is positive or negative I vectors don't have signs but their components do What you need to be able to do I Given starting/ending position, time, speed for one or more trip legs, calculate average -

Quadtree Displacement Mapping with Height Blending
Quadtree Displacement Mapping with Height Blending Practical Detailed Multi-Layer Surface Rendering Michal Drobot Technical Art Director Reality Pump Outline • Introduction • Motivation • Existing Solutions • Quad tree Displacement Mapping • Shadowing • Surface Blending • Conclusion Introduction • Next generation rendering – Higher quality per-pixel • More effects • Accurate computation – Less triangles, more sophistication • Ray tracing • Volumetric effects • Post processing – Real world details • Shadows • Lighting • Geometric properties Surface rendering • Surface rendering stuck at – Blinn/Phong • Simple lighting model – Normal mapping • Accounts for light interaction modeling • Doesn’t exhibit geometric surface depth – Industry proven standard • Fast, cheap, but we want more… Terrain surface rendering • Rendering terrain surface is costly – Requires blending • With current techniques prohibitive – Blend surface exhibit high geometric complexity Surface properties • Surface geometric properties – Volume – Depth – Various frequency details • Together they model visual clues – Depth parallax – Self shadowing – Light Reactivity Surface Rendering • Light interactions – Depends on surface microstructure – Many analytic solutions exists • Cook Torrance BDRF • Modeling geometric complexity – Triangle approach • Costly – Vertex transform – Memory • More useful with Tessellation (DX 10.1/11) – Ray tracing Motivation • Render different surfaces – Terrains – Objects – Dynamic Objects • Fluid/Gas simulation • Do it fast – Current Hardware – Consoles -

Oscillations
CHAPTER FOURTEEN OSCILLATIONS 14.1 INTRODUCTION In our daily life we come across various kinds of motions. You have already learnt about some of them, e.g., rectilinear 14.1 Introduction motion and motion of a projectile. Both these motions are 14.2 Periodic and oscillatory non-repetitive. We have also learnt about uniform circular motions motion and orbital motion of planets in the solar system. In 14.3 Simple harmonic motion these cases, the motion is repeated after a certain interval of 14.4 Simple harmonic motion time, that is, it is periodic. In your childhood, you must have and uniform circular enjoyed rocking in a cradle or swinging on a swing. Both motion these motions are repetitive in nature but different from the 14.5 Velocity and acceleration periodic motion of a planet. Here, the object moves to and fro in simple harmonic motion about a mean position. The pendulum of a wall clock executes 14.6 Force law for simple a similar motion. Examples of such periodic to and fro harmonic motion motion abound: a boat tossing up and down in a river, the 14.7 Energy in simple harmonic piston in a steam engine going back and forth, etc. Such a motion motion is termed as oscillatory motion. In this chapter we 14.8 Some systems executing study this motion. simple harmonic motion The study of oscillatory motion is basic to physics; its 14.9 Damped simple harmonic motion concepts are required for the understanding of many physical 14.10 Forced oscillations and phenomena. In musical instruments, like the sitar, the guitar resonance or the violin, we come across vibrating strings that produce pleasing sounds. -
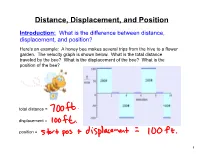
Distance, Displacement, and Position
Distance, Displacement, and Position Introduction: What is the difference between distance, displacement, and position? Here's an example: A honey bee makes several trips from the hive to a flower garden. The velocity graph is shown below. What is the total distance traveled by the bee? What is the displacement of the bee? What is the position of the bee? total distance = displacement = position = 1 Warm-up A particle moves along the x-axis so that the acceleration at any time t is given by: At time , the velocity of the particle is and at time , the position is . (a) Write an expression for the velocity of the particle at any time . (b) For what values of is the particle at rest? (c) Write an expression for the position of the particle at any time . (d) Find the total distance traveled by the particle from to . 2 Warm-up Answers (a) (b) (c) (d) Total Distance = 3 Now, using the equation from the warm-up find the following (WITHOUT A CALCULATOR): (a) the total distance from 0 to 4 (b) the displacement from 0 to 4 4 To find the displacement (position shift) from the velocity function, we just integrate the function. The negative areas below the x-axis subtract from the total displacement. Displacement = To find the distance traveled we have to use absolute value. Distance traveled = To find the distance traveled by hand you must: Find the roots of the velocity equation and integrate in pieces, just like when we found the area between a curve and x-axis. -

Force-Based Element Vs. Displacement-Based Element
Force-based Element vs. Displacement-based Element Vesna Terzic UC Berkeley December 2011 Agenda • Introduction • Theory of force-based element (FBE) • Theory of displacement-based element (DBE) • Examples • Summary and conclusions • Q & A with web participants Introduction • Contrary to concentrated plasticity models (elastic element with rotational springs at element ends) force-based element (FBE) and displacement- based element (DBE) permit spread of plasticity along the element (distributed plasticity models). • Distributed plasticity models allow yielding to occur at any location along the element, which is especially important in the presence of distributed element loads (girders with high gravity loads). Introduction • OpenSees commands for defining FBE and DBE have the same arguments: element forceBeamColumn $eleTag $iNode $jNode $numIntgrPts $secTag $transfTag element displacementBeamColumn $eleTag $iNode $jNode $numIntgrPts $secTag $transfTag • However a beam-column element needs to be modeled differently using these two elements to achieve a comparable level of accuracy. • The intent of this seminar is to show users how to properly model frame elements with both FBE and DBE. • In order to enhance your understanding of these two elements and to assure their correct application I will present the theory of these two elements and demonstrate their application on two examples. Transformation of global to basic system Element u p u p p aT q v = af u GeometricTran = f q3,v3 q1,v1 v q Basic System q2,v 2 Displacement-based element • The displacement-based approach follows standard finite element procedures where we interpolate section deformations from an approximate displacement field then use the PVD to form the element equilibrium relationship. -

Angular Kinematics Contents of the Lesson
Angular Kinematics Contents of the Lesson Angular Motion and Kinematics Angular Distance and Angular Displacement. Angular Speed and Angular Velocity Angular Acceleration Questions. Motion “change in the position of an object with respect to some reference frame.” Planes and Axis. Angular Motion “Rotation of a object around a central imaginary line” Characteristics: ◦ Axis of rotation. ◦ Whole object moves. Identify the angular motion Angular motion in the human body “most of movement are angular” In the human body; ◦ Joint= Axis of rotation. ◦ Body segment= object or rotatory body. ◦ Initial position= anatomical position. Kinematics; Angular Kinematics “Description of Angular Motion” Seeks to answer? “How much something has rotated?” “How fast something is rotating?” etc. Units of measurements Degrees. Radian Units of measurement Revolutions 1 revolution= 1 circle= 360 degrees= 2휋.radians Angular Distance “Sum of all angular changes undergone by a rotatory body” Unit: degrees, radian revolution. Angular Displacement “difference between the initial and final position of a rotatory body around an axis of rotation with regards to direction.” Direction= counter clockwise or clockwise In Human movement= Flexion,Extension,etc. What will be the angular displacement? Angular Speed “Scalar quantity” “angular distance covered divided by time interval over which the motion occurred” Angular Velocity “Vector quantity” “rate of change of angular position or angular displacement w.r.t time” Angular speed and Velocity Angular speed = degree/sec, rad/sec, or revolution/sec. Angular Velocity= degree/sec, rad/sec, or revolution/sec counterclockwise, clockwise or flexion or extension, etc. Angular Acceleration “Rate of change of angular velocity w.r.t time.” Unit= degree/sec² Calculate acceleration. -

Dynamic Image-Space Per-Pixel Displacement Mapping With
ThoseThose DeliciousDelicious TexelsTexels…… or… DynamicDynamic ImageImage--SpaceSpace PerPer--PixelPixel DisplacementDisplacement MappingMapping withwith SilhouetteSilhouette AntialiasingAntialiasing viavia ParallaxParallax OcclusionOcclusion MappingMapping Natalya Tatarchuk 3D Application Research Group ATI Research, Inc. OverviewOverview ofof thethe TalkTalk > The goal > Overview of approaches to simulate surface detail > Parallax occlusion mapping > Theory overview > Algorithm details > Performance analysis and optimizations > In the demo > Art considerations > Uses and future work > Conclusions Game Developer Conference, San Francisco, CA, March 2005 2 WhatWhat ExactlyExactly IsIs thethe Problem?Problem? > We want to render very detailed surfaces > Don’t want to pay the price of millions of triangles > Vertex transform cost > Memory > Want to render those detailed surfaces correctly > Preserve depth at all angles > Dynamic lighting > Self occlusion resulting in correct shadowing > Thirsty graphics cards want more ALU operations (and they can handle them!) > Of course, this is a balancing game - fill versus vertex transform – you judge for yourself what’s best Game Developer Conference, San Francisco, CA, March 2005 3 ThisThis isis NotNot YourYour TypicalTypical ParallaxParallax Mapping!Mapping! > Parallax Occlusion Mapping is a new technique > Different from > Parallax Mapping > Relief Texture Mapping > Per-pixel ray tracing at its core > There are some very recent similar techniques > Correctly handles complicated viewing phenomena -

Per-Pixel Displacement Mapping with Distance Functions
108_gems2_ch08_new.qxp 2/2/2005 2:20 PM Page 123 Chapter 8 Per-Pixel Displacement Mapping with Distance Functions William Donnelly University of Waterloo In this chapter, we present distance mapping, a technique for adding small-scale dis- placement mapping to objects in a pixel shader. We treat displacement mapping as a ray-tracing problem, beginning with texture coordinates on the base surface and calcu- lating texture coordinates where the viewing ray intersects the displaced surface. For this purpose, we precompute a three-dimensional distance map, which gives a measure of the distance between points in space and the displaced surface. This distance map gives us all the information necessary to quickly intersect a ray with the surface. Our algorithm significantly increases the perceived geometric complexity of a scene while maintaining real-time performance. 8.1 Introduction Cook (1984) introduced displacement mapping as a method for adding small-scale detail to surfaces. Unlike bump mapping, which affects only the shading of surfaces, displacement mapping adjusts the positions of surface elements. This leads to effects not possible with bump mapping, such as surface features that occlude each other and nonpolygonal silhouettes. Figure 8-1 shows a rendering of a stone surface in which occlusion between features contributes to the illusion of depth. The usual implementation of displacement mapping iteratively tessellates a base sur- face, pushing vertices out along the normal of the base surface, and continuing until 8.1 Introduction 123 Copyright 2005 by NVIDIA Corporation 108_gems2_ch08_new.qxp 2/2/2005 2:20 PM Page 124 Figure 8-1. A Displaced Stone Surface Displacement mapping (top) gives an illusion of depth not possible with bump mapping alone (bottom). -

Analysis on Torque, Flowrate, and Volumetric Displacement of Gerotor Pump/Motor
연구논문 Journal of Drive and Control, Vol.17 No.2 pp.28-37 Jun. 2020 ISSN 2671-7972(print) ISSN 2671-7980(online) http://dx.doi.org/10.7839/ksfc.2020.17.2.028 Analysis on Torque, Flowrate, and Volumetric Displacement of Gerotor Pump/Motor Hongsik Yun1, Young-Bog Ham2 and Sungdong Kim1* Received: 02 Apr. 2020, Revised: 14 May 2020, Accepted: 18 May 2020 Key Words:Torque Equilibrium, Energy Conservation, Volumetric Displacement, Flowrate, Rotation Speed, Gerotor Pump/Motor Abstract: It is difficult to analytically derive the relationship among volumetric displacement, flowrate, torque, and rotation speed regarding an instantaneous position of gerotor hydraulic pumps/motors. This can be explained by the geometric shape of the rotors, which is highly complicated. Herein, an analytical method for the instantaneous torque, rotation speed, flowrate, and volumetric displacement of a pump/motor is proposed. The method is based on two physical concepts: energy conservation and torque equilibrium. The instantaneous torque of a pump/motor shaft is determined for the posture of rotors from the torque equilibrium. If the torque equilibrium is combined with the energy conservation between the hydraulic energy of the pump/motor and the mechanical input/output energy, the formula for determining the instantaneous volumetric displacement and flowrate is derived. The numerical values of the instantaneous volumetric displacement, torque, rotation speed, and flowrate are calculated via the MATLAB software programs, and they are illustrated for the case in which inner and outer rotors rotate with respect to fixed axes. The degrees of torque fluctuation, speed fluctuation, and flowrate fluctuation can be observed from their instantaneous values. -

Analytic Displacement Mapping Using Hardware Tessellation
Analytic Displacement Mapping using Hardware Tessellation Matthias Nießner University of Erlangen-Nuremberg and Charles Loop Microsoft Research Displacement mapping is ideal for modern GPUs since it enables high- 1. INTRODUCTION frequency geometric surface detail on models with low memory I/O. How- ever, problems such as texture seams, normal re-computation, and under- Displacement mapping has been used as a means of efficiently rep- sampling artifacts have limited its adoption. We provide a comprehensive resenting and animating 3D objects with high frequency surface solution to these problems by introducing a smooth analytic displacement detail. Where texture mapping assigns color to surface points at function. Coefficients are stored in a GPU-friendly tile based texture format, u; v parameter values, displacement mapping assigns vector off- and a multi-resolution mip hierarchy of this function is formed. We propose sets. The advantages of this approach are two-fold. First, only the a novel level-of-detail scheme by computing per vertex adaptive tessellation vertices of a coarse (low frequency) base mesh need to be updated factors and select the appropriate pre-filtered mip levels of the displace- each frame to animate the model. Second, since the only connec- ment function. Our method obviates the need for a pre-computed normal tivity data needed is for the coarse base mesh, significantly less map since normals are directly derived from the displacements. Thus, we space is needed to store the equivalent highly detailed mesh. Fur- are able to perform authoring and rendering simultaneously without typical ther space reductions are realized by storing scalar, rather than vec- displacement map extraction from a dense triangle mesh.