And Multipolar Neurons7 2.1
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Nervous Tissue
Nervous Tissue Prof.Prof. ZhouZhou LiLi Dept.Dept. ofof HistologyHistology andand EmbryologyEmbryology Organization:Organization: neuronsneurons (nerve(nerve cells)cells) neuroglialneuroglial cellscells Function:Function: Ⅰ Neurons 1.1. structurestructure ofof neuronneuron somasoma neuriteneurite a.a. dendritedendrite b.b. axonaxon 1.11.1 somasoma (1)(1) nucleusnucleus LocatedLocated inin thethe centercenter ofof soma,soma, largelarge andand palepale--stainingstaining nucleusnucleus ProminentProminent nucleolusnucleolus (2)(2) cytoplasmcytoplasm (perikaryon)(perikaryon) a.a. NisslNissl bodybody b.b. neurofibrilneurofibril NisslNissl’’ss bodiesbodies LM:LM: basophilicbasophilic massmass oror granulesgranules Nissl’s Body (TEM) EMEM:: RERRER,, freefree RbRb FunctionFunction:: producingproducing thethe proteinprotein ofof neuronneuron structurestructure andand enzymeenzyme producingproducing thethe neurotransmitterneurotransmitter NeurofibrilNeurofibril thethe structurestructure LM:LM: EM:EM: NeurofilamentNeurofilament micmicrotubulerotubule FunctionFunction cytoskeleton,cytoskeleton, toto participateparticipate inin substancesubstance transporttransport LipofuscinLipofuscin (3)(3) CellCell membranemembrane excitableexcitable membranemembrane ,, receivingreceiving stimutation,stimutation, fromingfroming andand conductingconducting nervenerve impulesimpules neurite: 1.2 Dendrite dendritic spine spine apparatus Function: 1.3 Axon axon hillock, axon terminal, axolemma Axoplasm: microfilament, microtubules, neurofilament, mitochondria, -

Neurons and Glia
CHAPTER TWO Neurons and Glia INTRODUCTION THE NEURON DOCTRINE The Golgi Stain Cajal’s Contribution BOX 2.1 OF SPECIAL INTEREST: Advances in Microscopy THE PROTOTYPICAL NEURON The Soma The Nucleus Neuronal Genes, Genetic Variation, and Genetic Engineering BOX 2.2 BRAIN FOOD: Expressing One’s Mind in the Post-Genomic Era BOX 2.3 PATH OF DISCOVERY: Gene Targeting in Mice, by Mario Capecchi Rough Endoplasmic Reticulum Smooth Endoplasmic Reticulum and the Golgi Apparatus The Mitochondrion The Neuronal Membrane The Cytoskeleton Microtubules BOX 2.4 OF SPECIAL INTEREST: Alzheimer’s Disease and the Neuronal Cytoskeleton Microfilaments Neurofilaments The Axon The Axon Terminal The Synapse Axoplasmic Transport BOX 2.5 OF SPECIAL INTEREST: Hitching a Ride with Retrograde Transport Dendrites BOX 2.6 OF SPECIAL INTEREST: Intellectual Disability and Dendritic Spines CLASSIFYING NEURONS Classification Based on Neuronal Structure Number of Neurites Dendrites Connections Axon Length Classification Based on Gene Expression BOX 2.7 BRAIN FOOD: Understanding Neuronal Structure and Function with Incredible Cre GLIA Astrocytes Myelinating Glia Other Non-Neuronal Cells CONCLUDING REMARKS 23 © Jones & Bartlett Learning, LLC. NOT FOR SALE OR DISTRIBUTION. 24 PART ONE FOUNDATIONS INTRODUCTION All tissues and organs in the body consist of cells. The specialized func- tions of cells and how they interact determine the functions of organs. The brain is an organ—to be sure, the most sophisticated and complex organ that nature has devised. But the basic strategy for unraveling its functions is no different from that used to investigate the pancreas or the lung. We must begin by learning how brain cells work individually and then see how they are assembled to work together. -

Synaptic Mechanisms of Bipolar Cell Terminals
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Vision Research 39 (1999) 2469–2476 Synaptic mechanisms of bipolar cell terminals Gary Matthews * Department of Neurobiology and Beha6ior, State Uni6ersity of New York, Stony Brook, NY 11794-5230, USA Received 8 May 1998; received in revised form 24 August 1998 Abstract Giant synaptic terminals of goldfish bipolar neurons allow direct studies of presynaptic mechanisms underlying neurotransmit- ter release and its modulation. Calcium influx via L-type calcium channels of the terminal triggers synaptic vesicle exocytosis, which can be monitored in isolated terminals by means of the associated changes in membrane capacitance. Information about the kinetics and calcium dependence of synaptic exocytosis has been obtained from capacitance measurements in these ribbon-type synaptic terminals. © 1999 Elsevier Science Ltd. All rights reserved. Keywords: Synaptic mechanisms; Terminals; Bipolar neurons Studies of presynaptic mechanisms in the vertebrate enzymatic digestion of goldfish retina or in single, central nervous system (CNS) are complicated by the isolated terminals. Consistent with their central role in small size of most CNS synaptic terminals. However, neurotransmitter release, voltage-dependent calcium several notable exceptions allow direct electrical mea- channels are located predominantly in the synaptic surements to be made from single terminals, including terminal of the bipolar cell (Tachibana & Okada, 1991; giant -
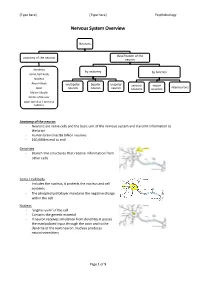
Nervous System Overview
[Type here] [Type here] Psychobiology Nervous System Overview Neurons classification of the anatomy of the neuron neuron dendrites by anatomy by function soma /cell body Nucleus Axon Hillock multipolar bipolar unipolar sensory motor interneurons Axon neuron neuron neuron neurons neurons Mylein Sheath Nodes of Ranvier Axon terminal / terminal buttons Anatomy of the neuron - Neurons are nerve cells and the basic unit of the nervous system and transmit information to the brain - Human brains has 86 billion neurons - 160,000km end to end Dendrites - Branch like structures that receive information from other cells Soma / Cell body - Includes the nucleus, it protects the nucleus and cell contents - The phospholipid bilayer maintains the negative charge within the cell Nucleus - ‘engine room’ of the cell - Contains the genetic material - If neuron receives simulation from dendrites it passes the manipulated input through the axon and to the dendrite of the next neuron. Nucleus produces neurotransmitters Page 1 of 5 [Type here] [Type here] Psychobiology Axon Hillock - The gatekeeper of transmission: this is where it is decided whether or not action potential is fired Axon terminals/ terminal buttons - Chemical messages are sent from these terminals - Gap between neurons are called synapses. Axon terminals are considered ‘pre-synaptic’ and dendrites are ‘post-synaptic’ Axon - Long nerve fibre - Transmits information to other neurons - Conducts the electrical signals from the cell body Myelin sheath - Coating that insulates the axon, composed of primarily of lipids (fats) - Allows for faster signalling - Produced by Schwan cells - Myelinated axons give some portions of the brain a white appearance Nodes of Ranvier - Bare axon - Allows the transmission to continue down the axon Classification of Neuron by Anatomy Multipolar Neuron Bipolar Neuron Unipolar Neuron - Long axon and lots of - 2 extensions from - 1 extension from the dendrites cell body cell body - (i.e. -

Notch-Signaling in Retinal Regeneration and Müller Glial Plasticity
Notch-Signaling in Retinal Regeneration and Müller glial Plasticity DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Kanika Ghai, MS Neuroscience Graduate Studies Program The Ohio State University 2009 Dissertation Committee: Dr. Andy J Fischer, Advisor Dr. Heithem El-Hodiri Dr. Susan Cole Dr. Paul Henion Copyright by Kanika Ghai 2009 ABSTRACT Eye diseases such as blindness, age-related macular degeneration (AMD), diabetic retinopathy and glaucoma are highly prevalent in the developed world, especially in a rapidly aging population. These sight-threatening diseases all involve the progressive loss of cells from the retina, the light-sensing neural tissue that lines the back of the eye. Thus, developing strategies to replace dying retinal cells or prolonging neuronal survival is essential to preserving sight. In this regard, cell-based therapies hold great potential as a treatment for retinal diseases. One strategy is to stimulate cells within the retina to produce new neurons. This dissertation elucidates the properties of the primary support cell in the chicken retina, known as the Müller glia, which have recently been shown to possess stem-cell like properties, with the potential to form new neurons in damaged retinas. However, the mechanisms that govern this stem-cell like ability are less well understood. In order to better understand these properties, we analyze the role of one of the key developmental processes, i.e., the Notch-Signaling Pathway in regulating proliferative, neuroprotective and regenerative properties of Müller glia and bestow them with this plasticity. -

Microcircuitry of Bipolar Cells in Cat Retina1
0270.6474/84/0412-2920$02.00/0 The Journal of Neuroscience Copyright 0 Society for Neuroscience Vol. 4, No. 12, pp. 2920-2938 Printed in U.S.A. December 1984 MICROCIRCUITRY OF BIPOLAR CELLS IN CAT RETINA1 BARBARA A. McGUIRE,’ JOHN K. STEVENS,3 AND PETER STERLING Department of Anatomy, School of Medicine, University of Pennsylvania, Philadelphia, Pennsylvania 19104 Received October 31, 1983; Revised June 4, 1984; Accepted June 6, 1984 Abstract We have studied 15 bipolar neurons from a small patch (14 x 120 Frn) of adult cat retina located within the area centralis. From electron micrographs of 189 serial ultrathin sections, the axon of each bipolar cell was substantially reconstructed with its synaptic inputs and outputs by means of a computer-controlled reconstruc- tion system. Based on differences in stratification, cytology, and synaptic connections, we identified eight different cell types among the group of 15 neurons: one type of rod bipolar and seven types of cone bipolar neurons. These types correspond to those identified by the Golgi method and by intracellular recording. Those bipolar cell types for which we reconstructed three or four examples were extremely regular in form, size, and cytology, and also in the quantitative details of their synaptic connections. They appeared quite as specific in these respects as invertebrate “identified” neurons. The synaptic patterns observed for each type of bipolar neuron were complex but may be summarized as follows: the rod bipolar axon ended in sublamina b of the inner plexiform layer and provided major input to the AI1 amacrine cell. The axons of three types of cone bipolar cells also terminated in sublamina b and provided contacts to dendrites of on-6 and other ganglion cells. -

The Diverse Roles of Ribbon Synapses in Sensory Neurotransmission
Nature Reviews Neuroscience | AOP, published online 3 November 2010; doi:10.1038/nrn2924 REVIEWS The diverse roles of ribbon synapses in sensory neurotransmission Gary Matthews* and Paul Fuchs‡ Abstract | Sensory synapses of the visual and auditory systems must faithfully encode a wide dynamic range of graded signals, and must be capable of sustained transmitter release over long periods of time. Functionally and morphologically, these sensory synapses are unique: their active zones are specialized in several ways for sustained, rapid vesicle exocytosis, but their most striking feature is an organelle called the synaptic ribbon, which is a proteinaceous structure that extends into the cytoplasm at the active zone and tethers a large pool of releasable vesicles. But precisely how does the ribbon function to support tonic release at these synapses? Recent genetic and biophysical advances have begun to open the ‘black box’ of the synaptic ribbon with some surprising findings and promise to resolve its function in vision and hearing. Changes in our external environment are detected by photoreceptors, electroreceptors, and hair cells of sensory receptor cells, which transduce sensory stim- vesti bular organs and the lateral line system. In the uli into an electrical signal that is graded depending visual system, ribbons are also found at the output on the stimulus intensity. In vision, balance and hear- synapses of the second-order retinal b ipolar neurons, ing, synapses of the receptor cells are unusual because which signal by means of graded changes in mem- they function tonically — that is, they transmit graded brane potential, similar to photoreceptors and hair information with high fidelity across a broad range of cells. -

The Human Brain Miguel Marín-Padilla
The Human Brain Miguel Marín-Padilla The Human Brain Prenatal Development and Structure Author Miguel Marín-Padilla Timberlea Circle 2447 55125 Woodbury, MN USA [email protected] ISBN 978-3-642-14723-4 e-ISBN 978-3-642-14724-1 DOI 10.1007/978-3-642-14724-1 Springer Heidelberg Dordrecht London New York Library of Congress Control Number: 2010936628 © Springer-Verlag Berlin Heidelberg 2011 This work is subject to copyright. All rights are reserved, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilm or in any other way, and storage in data banks. Duplication of this publication or parts thereof is permitted only under the provisions of the German Copyright Law of September 9, 1965, in its current version, and permission for use must always be obtained from Springer. Violations are liable to prosecution under the German Copyright Law. The use of general descriptive names, registered names, trademarks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use. Product liability: The publishers cannot guarantee the accuracy of any information about dosage and appli- cation contained in this book. In every individual case the user must check such information by consulting the relevant literature. Cover design: eStudioCalamar, Figueres/Berlin Printed on acid-free paper Springer is part of Springer Science+Business Media (www.springer.com) I dedicated this monograph to the memory of my dear Teresa, spouse, mother of my children, friend and life-long companion, since student years. -

The Unipolar Neuron
The Unipolar Neuron The unipolar neuron is a sensory neuron and carries an electrical signal to the CNS. However, the anatomy of unipolar neurons is subject to different interpretations. As the unipolar neuron develops, there is a single protoplasmic process which extends from the neuron’s soma. This process splits immediately into two segments: 1) a proximal segment which enters the spinal cord; 2) a distal segment which extends out into the body and terminates in tissue as a “receptor”. Some refer to the two processes as “axons” while others refer to only the proximal process as an axon and the distal process as the dendrite. Saladin chooses the former while others (including myself!) choose the latter interpretation. Here is the critical issue. The receptor (i.e. dendrite) in the target tissue is stimulated and generates an action potential that moves towards the spinal cord (either in the dendrite or axon depending on which interpretation you choose). As the electrical signal approaches the soma, it does not need to create a local potential within the soma and the action potential continues to propagate the signal beyond the protoplasmic process of the soma. At the point of the soma’s protoplasmic process, the action potential does not enter the soma, but simply continues uninterrupted along the path to the spinal cord. Competing Definitions: 1. Unipolar neurons have but one process from the cell body. However, that single, very short, process splits into longer processes (a dendrite plus an axon). Unipolar neurons are sensory neurons - conducting impulses into the central nervous system. -

Normal Cells of the Cns
NORMAL CELLS OF THE CNS Color index: Slides.. Important ..Notes ..Extra.. Objectives: At the end of this lecture, you should describe the microscopic structure and the function of: 1- Neurons: Cell body (perikaryon). Processes: An axon and dendrites. 2- Neuroglia: Astrocytes. Oligodendrocytes. Microglia. Ependymal cells. Axon: only one Processes Neuron components Dendrites: one or more Cell body (Perikaryon) Types of neurons based on number of processes: Unipolar neuron Has one process only, that divides into two branches; (Pseudounipolar) one acts as a dendrite and the other as an axon. (rounded neuron) e.g. Mesencephalic nucleus of trigeminal nerve Not directly connected to the cell body and dorsal root (spinal) ganglion. Bipolar Neuron Has two processes (one arising from each pole of the cell body) (spindle-shaped neuron) One of them is the dendrite and the other is the axon. like having 2 necks e.g. retina & olfactory epithelium. Multipolar neuron: Stellate Neurons (star shape) Pyramidal Neurons (wide base) Pyriform Neurons Has one axon and multiple - The commonest type. - Distributed in motor area 4 - Pear-shaped dendrites. - Distributed in most areas of CNS of the cerebral cortex. e.g. Purkinje cells of cerebellar -Its outline is irregular in shape e.g. anterior horn cells of the -Neuroglial cells are much more cortex. number than neurons in the CNS spinal cord. they can divide and regenerate normally. Cell body (perikaryon) Cytoplasm: Cytoplasm with mitochondria and ribosomes and rough Nucleus: ER only in dendrites not in axons Single, usually central, rounded and Its main components include: vesicular with prominent nucleolus. Nissl Neuro- Micro- Golgi Mito- Centriole Pigments Other bodies filaments tubles apparatus chondria Depend on age Are * Are Most basophilic intermediate *lipofuscin patches of filaments adult pigment: in rough which are Are neurons old age bundled Endoplasmic found in have Some fat Reticulum together to the cell Surrounds *Melanin (rER) and form the Are only one and rudimentary pigments: in free neurofibrils. -

Name HST 131/Neuro 200 Exam III, Nov 19
Harvard-MIT Division of Health Sciences and Technology HST.131: Introduction to Neuroscience Course Director: Dr. David Corey Name ___________________________ HST 131/Neuro 200 (write your name on every sheet) Exam III, Nov 19, 2004 There are 28 questions. Point values for each are given. 86 points total. 1. The dark current of photoreceptors is so named since it flows in the dark. It was initially recorded between two extracellular electrodes one placed at the outer segment, and the other placed nearer to the inner segment. What ionic current is being measured here? (3 points): a. Ion responsible: __________ b. Type of channel responsible: __________ c. Subcellular localization of channel: __________ 2. Following the interaction of rhodopsin with light, which of the following play a rolein stopping the downstream signaling? (3 points) a. The G-protein coupled receptor transducin is hydrolyzes its GTP and ceases to signal. b. Active rhodopsin eventually hydrolyses its GTP and ceases to signal. c. Active transducin is phosphorylated by opsin kinase and then inactived by arrestin. d. Active rhodopsin is phosphorylated by opsin kinase and then inactived by arrestin. e. Active rhodopsin is phosphorylated by opsin kinase and then endocytosed. f. Activation of a phosphodiesterase reduces intracellular cGMP and closes gates of cyclic nucleotide gated channels. 3. Sensory adaptation in the retina occurs since (2 points): a. Calcium influx through cGMP gated channels is reduced during prolonged light exposure. Resting calcum is reduced, which disinhibits guanylyl cyclase and modestly increases cGMP concentration in the photoreceptor. b. The center-surround structure of horizontal cells tends to reduce signals in response to only extremely bright light, always resulting in an intermediate firing pattern in retinal ganglion cells. -

Guillain-Barre Syndrome (GBS)
Nervous tissue Anatomically Central nervous system (CNS) brain and spinal cord Peripheral nervous system (PNS) - cranial, spinal, and peripheral nerves - ganglia: nerve cell bodies outside the CNS Major cell types Neuron: nerve cell Supporting / Glial cells - Schwann cells, satellite cells (in PNS) - glia/neuroglia (in CNS) Neurone / Neuron Cell body Nucleus Cytoplasm (perikaryon) Process Axon Dendrites Axons (nerve fibers) Axon hillock Terminal boutons Dorsal root ganglia (DRG) nucleus ganglion/ganglia DRG neurons Basic neuron types Multipolar neuron Multiple dendrites Single axons Types: Interneurons Motor neurons Sympathetic neurons Bipolar neuron Single dendrite Single axon Types: Receptor neurons Vision Smell Balance Pseudo-unipolar neuron peripheral Single axon (Stem process) with stem 2 branches: Central process to spinal cord Peripheral process to terminal tissues (muscle, joints, skin et al) functionally: dendrite structurally: axon Type: Dorsal root ganglia (DRG neuron) central Pseudo-unipolar neuron Neuron: ultrastructure Rough endoplamic reticulum (rER) Nissl substance Cytoskeleton Microtubule Intermediate filaments: Neurofilaments Microfilaments: Actin Specialization of neuron/axon Cytoskeleton Axonal transport Neuron: ultrastructure rER: rough ER M: mitochondria L: lysosome G: Golgi Microscopic methods H & E (Hematoxylin and eosin) Nissl method Heavy metal impregnation Golgi, Cajal Thick sections / Spread preparations gold, silver: deposited in microtubules / neurofilaments Immunohistochemistry Microscopic methods: H & E