Tree: Classification and Regression Trees
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
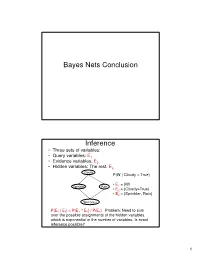
Bayes Nets Conclusion Inference
Bayes Nets Conclusion Inference • Three sets of variables: • Query variables: E1 • Evidence variables: E2 • Hidden variables: The rest, E3 Cloudy P(W | Cloudy = True) • E = {W} Sprinkler Rain 1 • E2 = {Cloudy=True} • E3 = {Sprinkler, Rain} Wet Grass P(E 1 | E 2) = P(E 1 ^ E 2) / P(E 2) Problem: Need to sum over the possible assignments of the hidden variables, which is exponential in the number of variables. Is exact inference possible? 1 A Simple Case A B C D • Suppose that we want to compute P(D = d) from this network. A Simple Case A B C D • Compute P(D = d) by summing the joint probability over all possible values of the remaining variables A, B, and C: P(D === d) === ∑∑∑ P(A === a, B === b,C === c, D === d) a,b,c 2 A Simple Case A B C D • Decompose the joint by using the fact that it is the product of terms of the form: P(X | Parents(X)) P(D === d) === ∑∑∑ P(D === d | C === c)P(C === c | B === b)P(B === b | A === a)P(A === a) a,b,c A Simple Case A B C D • We can avoid computing the sum for all possible triplets ( A,B,C) by distributing the sums inside the product P(D === d) === ∑∑∑ P(D === d | C === c)∑∑∑P(C === c | B === b)∑∑∑P(B === b| A === a)P(A === a) c b a 3 A Simple Case A B C D This term depends only on B and can be written as a 2- valued function fA(b) P(D === d) === ∑∑∑ P(D === d | C === c)∑∑∑P(C === c | B === b)∑∑∑P(B === b| A === a)P(A === a) c b a A Simple Case A B C D This term depends only on c and can be written as a 2- valued function fB(c) === === === === === === P(D d) ∑∑∑ P(D d | C c)∑∑∑P(C c | B b)f A(b) c b …. -

How to Find out the IP Address of an Omron
Communications Middleware/Network Browser How to find an Omron Controller’s IP address Valin Corporation | www.valin.com Overview • Many Omron PLC’s have Ethernet ports or Ethernet port options • The IP address for a PLC is usually changed by the programmer • Most customers do not mark the controller with IP address (label etc.) • Very difficult to communicate to the PLC over Ethernet if the IP address is unknown. Valin Corporation | www.valin.com Simple Ethernet Network Basics IP address is up to 12 digits (4 octets) Ex:192.168.1.1 For MOST PLC programming applications, the first 3 octets are the network address and the last is the node address. In above example 192.168.1 is network address, 1 is node address. For devices to communicate on a simple network: • Every device IP Network address must be the same. • Every device node number must be different. Device Laptop EX: Omron PLC 192.168.1.1 192.168.1.1 Device Laptop EX: Omron PLC 127.27.250.5 192.168.1.1 Device Laptop EX: Omron PLC 192.168.1.3 192.168.1.1 Valin Corporation | www.valin.com Omron Default IP Address • Most Omron Ethernet devices use one of the following IP addresses by default. Omron PLC 192.168.250.1 OR 192.168.1.1 Valin Corporation | www.valin.com PING Command • PING is a way to check if the device is connected (both virtually and physically) to the network. • Windows Command Prompt command. • PC must use the same network number as device (See previous) • Example: “ping 172.21.90.5” will test to see if a device with that IP address is connected to the PC. -

Disk Clone Industrial
Disk Clone Industrial USER MANUAL Ver. 1.0.0 Updated: 9 June 2020 | Contents | ii Contents Legal Statement............................................................................... 4 Introduction......................................................................................4 Cloning Data.................................................................................................................................... 4 Erasing Confidential Data..................................................................................................................5 Disk Clone Overview.......................................................................6 System Requirements....................................................................................................................... 7 Software Licensing........................................................................................................................... 7 Software Updates............................................................................................................................. 8 Getting Started.................................................................................9 Disk Clone Installation and Distribution.......................................................................................... 12 Launching and initial Configuration..................................................................................................12 Navigating Disk Clone.....................................................................................................................14 -

Tree-Combined Trie: a Compressed Data Structure for Fast IP Address Lookup
(IJACSA) International Journal of Advanced Computer Science and Applications, Vol. 6, No. 12, 2015 Tree-Combined Trie: A Compressed Data Structure for Fast IP Address Lookup Muhammad Tahir Shakil Ahmed Department of Computer Engineering, Department of Computer Engineering, Sir Syed University of Engineering and Technology, Sir Syed University of Engineering and Technology, Karachi Karachi Abstract—For meeting the requirements of the high-speed impact their forwarding capacity. In order to resolve two main Internet and satisfying the Internet users, building fast routers issues there are two possible solutions one is IPv6 IP with high-speed IP address lookup engine is inevitable. addressing scheme and second is Classless Inter-domain Regarding the unpredictable variations occurred in the Routing or CIDR. forwarding information during the time and space, the IP lookup algorithm should be able to customize itself with temporal and Finding a high-speed, memory-efficient and scalable IP spatial conditions. This paper proposes a new dynamic data address lookup method has been a great challenge especially structure for fast IP address lookup. This novel data structure is in the last decade (i.e. after introducing Classless Inter- a dynamic mixture of trees and tries which is called Tree- Domain Routing, CIDR, in 1994). In this paper, we will Combined Trie or simply TC-Trie. Binary sorted trees are more discuss only CIDR. In addition to these desirable features, advantageous than tries for representing a sparse population reconfigurability is also of great importance; true because while multibit tries have better performance than trees when a different points of this huge heterogeneous structure of population is dense. -

Heaps a Heap Is a Complete Binary Tree. a Max-Heap Is A
Heaps Heaps 1 A heap is a complete binary tree. A max-heap is a complete binary tree in which the value in each internal node is greater than or equal to the values in the children of that node. A min-heap is defined similarly. 97 Mapping the elements of 93 84 a heap into an array is trivial: if a node is stored at 90 79 83 81 index k, then its left child is stored at index 42 55 73 21 83 2k+1 and its right child at index 2k+2 01234567891011 97 93 84 90 79 83 81 42 55 73 21 83 CS@VT Data Structures & Algorithms ©2000-2009 McQuain Building a Heap Heaps 2 The fact that a heap is a complete binary tree allows it to be efficiently represented using a simple array. Given an array of N values, a heap containing those values can be built, in situ, by simply “sifting” each internal node down to its proper location: - start with the last 73 73 internal node * - swap the current 74 81 74 * 93 internal node with its larger child, if 79 90 93 79 90 81 necessary - then follow the swapped node down 73 * 93 - continue until all * internal nodes are 90 93 90 73 done 79 74 81 79 74 81 CS@VT Data Structures & Algorithms ©2000-2009 McQuain Heap Class Interface Heaps 3 We will consider a somewhat minimal maxheap class: public class BinaryHeap<T extends Comparable<? super T>> { private static final int DEFCAP = 10; // default array size private int size; // # elems in array private T [] elems; // array of elems public BinaryHeap() { . -

“Log” File in Stata
Updated July 2018 Creating a “Log” File in Stata This set of notes describes how to create a log file within the computer program Stata. It assumes that you have set Stata up on your computer (see the “Getting Started with Stata” handout), and that you have read in the set of data that you want to analyze (see the “Reading in Stata Format (.dta) Data Files” handout). A log file records all your Stata commands and output in a given session, with the exception of graphs. It is usually wise to retain a copy of the work that you’ve done on a given project, to refer to while you are writing up your findings, or later on when you are revising a paper. A log file is a separate file that has either a “.log” or “.smcl” extension. Saving the log as a .smcl file (“Stata Markup and Control Language file”) keeps the formatting from the Results window. It is recommended to save the log as a .log file. Although saving it as a .log file removes the formatting and saves the output in plain text format, it can be opened in most text editing programs. A .smcl file can only be opened in Stata. To create a log file: You may create a log file by typing log using ”filepath & filename” in the Stata Command box. On a PC: If one wanted to save a log file (.log) for a set of analyses on hard disk C:, in the folder “LOGS”, one would type log using "C:\LOGS\analysis_log.log" On a Mac: If one wanted to save a log file (.log) for a set of analyses in user1’s folder on the hard drive, in the folder “logs”, one would type log using "/Users/user1/logs/analysis_log.log" If you would like to replace an existing log file with a newer version add “replace” after the file name (Note: PC file path) log using "C:\LOGS\analysis_log.log", replace Alternately, you can use the menu: click on File, then on Log, then on Begin. -

Tree Structures
Tree Structures Definitions: o A tree is a connected acyclic graph. o A disconnected acyclic graph is called a forest o A tree is a connected digraph with these properties: . There is exactly one node (Root) with in-degree=0 . All other nodes have in-degree=1 . A leaf is a node with out-degree=0 . There is exactly one path from the root to any leaf o The degree of a tree is the maximum out-degree of the nodes in the tree. o If (X,Y) is a path: X is an ancestor of Y, and Y is a descendant of X. Root X Y CSci 1112 – Algorithms and Data Structures, A. Bellaachia Page 1 Level of a node: Level 0 or 1 1 or 2 2 or 3 3 or 4 Height or depth: o The depth of a node is the number of edges from the root to the node. o The root node has depth zero o The height of a node is the number of edges from the node to the deepest leaf. o The height of a tree is a height of the root. o The height of the root is the height of the tree o Leaf nodes have height zero o A tree with only a single node (hence both a root and leaf) has depth and height zero. o An empty tree (tree with no nodes) has depth and height −1. o It is the maximum level of any node in the tree. CSci 1112 – Algorithms and Data Structures, A. -

A Simple Linear-Time Algorithm for Finding Path-Decompostions of Small Width
Introduction Preliminary Definitions Pathwidth Algorithm Summary A Simple Linear-Time Algorithm for Finding Path-Decompostions of Small Width Kevin Cattell Michael J. Dinneen Michael R. Fellows Department of Computer Science University of Victoria Victoria, B.C. Canada V8W 3P6 Information Processing Letters 57 (1996) 197–203 Kevin Cattell, Michael J. Dinneen, Michael R. Fellows Linear-Time Path-Decomposition Algorithm Introduction Preliminary Definitions Pathwidth Algorithm Summary Outline 1 Introduction Motivation History 2 Preliminary Definitions Boundaried graphs Path-decompositions Topological tree obstructions 3 Pathwidth Algorithm Main result Linear-time algorithm Proof of correctness Other results Kevin Cattell, Michael J. Dinneen, Michael R. Fellows Linear-Time Path-Decomposition Algorithm Introduction Preliminary Definitions Motivation Pathwidth Algorithm History Summary Motivation Pathwidth is related to several VLSI layout problems: vertex separation link gate matrix layout edge search number ... Usefullness of bounded treewidth in: study of graph minors (Robertson and Seymour) input restrictions for many NP-complete problems (fixed-parameter complexity) Kevin Cattell, Michael J. Dinneen, Michael R. Fellows Linear-Time Path-Decomposition Algorithm Introduction Preliminary Definitions Motivation Pathwidth Algorithm History Summary History General problem(s) is NP-complete Input: Graph G, integer t Question: Is tree/path-width(G) ≤ t? Algorithmic development (fixed t): O(n2) nonconstructive treewidth algorithm by Robertson and Seymour (1986) O(nt+2) treewidth algorithm due to Arnberg, Corneil and Proskurowski (1987) O(n log n) treewidth algorithm due to Reed (1992) 2 O(2t n) treewidth algorithm due to Bodlaender (1993) O(n log2 n) pathwidth algorithm due to Ellis, Sudborough and Turner (1994) Kevin Cattell, Michael J. Dinneen, Michael R. -

Basic STATA Commands
Summer School on Capability and Multidimensional Poverty OPHI-HDCA, 2011 Oxford Poverty and Human Development Initiative (OPHI) http://ophi.qeh.ox.ac.uk Oxford Dept of International Development, Queen Elizabeth House, University of Oxford Basic STATA commands Typical STATA window Review Results Variables Commands Exploring your data Create a do file doedit Change your directory cd “c:\your directory” Open your database use database, clear Import from Excel (csv file) insheet using "filename.csv" Condition (after the following commands) if var1==3 or if var1==”male” Equivalence symbols: == equal; ~= not equal; != not equal; > greater than; >= greater than or equal; < less than; <= less than or equal; & and; | or. Weight [iw=weight] or [aw=weight] Browse your database browse Look for a variables lookfor “any word/topic” Summarize a variable (mean, standard su variable1 variable2 variable3 deviation, min. and max.) Tabulate a variable (per category) tab variable1 (add a second variables for cross tabs) Statistics for variables by subgroups tabstat variable1 variable2, s(n mean) by(group) Information of a variable (coding) codebook variable1, tab(99) Keep certain variables (use drop for the keep var1 var2 var3 opposite) Save a dataset save filename, [replace] Summer School on Capability and Multidimensional Poverty OPHI-HDCA, 2011 Creating Variables Generate a new variable (a number or a gen new_variable = 1 combinations of other variables) gen new_variable = variable1+ variable2 Generate a new variable conditional gen new_variable -

Forest Quickstart Guide for Linguists
Forest Quickstart Guide for Linguists Guido Vanden Wyngaerd [email protected] June 28, 2020 Contents 1 Introduction 1 2 Loading Forest 2 3 Basic Usage 2 4 Adjusting node spacing 4 5 Triangles 7 6 Unlabelled nodes 9 7 Horizontal alignment of terminals 10 8 Arrows 11 9 Highlighting 14 1 Introduction Forest is a package for drawing linguistic (and other) tree diagrams de- veloped by Sašo Živanović. This manual provides a quickstart guide for linguists with just the essential things that you need to get started. More 1 extensive documentation is available from the CTAN-archive. Forest is based on the TikZ package; more information about its commands, in par- ticular those controlling the appearance of the nodes, the arrows, and the highlighting can be found in the TikZ documentation. 2 Loading Forest In your preamble, put \usepackage[linguistics]{forest} The linguistics option makes for nice trees, in which the branches meet above the two nodes that they join; it will also align the example number (provided by linguex) with the top of the tree: (1) CP C IP I VP V NP 3 Basic Usage Forest uses a familiar labelled brackets syntax. The code below will out- put the tree in (1) above (\ex. requires the linguex package and provides the example number): \ex. \begin{forest} [CP[C][IP[I][VP[V][NP]]]] \end{forest} Forest will parse the above code without problem, but you are likely to soon get lost in your labelled brackets with more complicated trees if you write the code this way. The better alternative is to arrange the nodes over multiple lines: 2 \ex. -

Problem Solving and Unix Tools
Problem Solving and Unix Tools Command Shell versus Graphical User Interface • Ease of use • Interactive exploration • Scalability • Complexity • Repetition Example: Find all Tex files in a directory (and its subdirectories) that have not changed in the past 21 days. With an interactive file roller, it is easy to sort files by particular characteristics such as the file extension and the date. But this sorting does not apply to files within subdirectories of the current directory, and it is difficult to apply more than one sort criteria at a time. A command line interface allows us to construct a more complex search. In unix, we find the files we are after by executing the command, find /home/nolan/ -mtime +21 -name ’*.tex’ To find out more about a command you can read the online man pages man find or you can execute the command with the –help option. In this example, the standard output to the screen is piped into the more command which formats it to dispaly one screenful at a time. Hitting the space bar displays the next page of output, the return key displays the next line of output, and the ”q” key quits the display. find --help | more Construct Solution in Pieces • Solve a problem by breaking down into pieces and building back up • Typing vs automation • Error messages - experimentation 1 Example: Find all occurrences of a particular string in several files. The grep command searches the contents of files for a regular expression. In this case we search for the simple character string “/stat141/FINAL” in all files in the directory WebLog that begin with the filename “access”. -

Metadata for Everyone a Simple, Low-Cost Methodology Timothy D
SAS Global Forum 2008 Data Integration Paper 138-2008 Metadata for Everyone A Simple, Low-Cost Methodology Timothy D. Brown, Altoona, IA ABSTRACT In the context of Base SAS® programming, this paper uses “hardcoded” values as an introduction to “metadata” and the reasons for using it. It then describes a low cost and simple methodology for maintaining any kind of metadata. INTRODUCTION This discussion will take an indirect approach to defining metadata. It’ll describe the metadata which might be included, or hard-coded, in a Base SAS program and propose alternatives to storing and using the metadata. Outside of programs “data” and “code” are distinct. However within programs, the distinction gets blurred when data values, called “hardcoded” data, are included within the code. Hardcoded values include, but are not limited to: • Text constants, literals • Names of companies, people, organizations and places • Directory paths and file names • Parameters on SAS procedures such as WHERE, KEEP, DROP, RENAME, VARS, BY etc • Numeric constants including dates* • Statistical constants • Period begin and end dates • Mixed text and numeric values • Expressions in IF and WHERE clauses • What-if scenarios (* excluding dates which are derived logically using a SAS functions such as TODAY(), DATETIME(), INTNX and NXTPD) In addition, many small conversion, cross-reference and look-up tables, which might be hardcoded as SAS formats or read into a program from many different sources, work well as metadata and fit into this framework. Obviously, some hardcoded values might never change in the life of a program. So it might be prudent to leave some hardcoded values in the code.