DOCSLIB.ORG

Information to Users

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Information to Users INFORMATION TO USERS This manuscript has been reproduced from the microfilm master. UMI films the text directly from the original or copy submitted. Thus, some thesis and dissertation copies are in typewriter face, while others may be from any type of computer printer. The quality of this reproduction is dependent upon the quality of the copy submitted. Broken or indistinct print, colored or poor quality illustrations and photographs, print bleedthrough, substandard margins, and improper alignment can adversely affect reproduction. In the unlikely event that the author did not send UMI a complete manuscript and there are missing pages, these will be noted. Also, if unauthorized copyright material had to be removed, a note will indicate the deletion. Oversize materials (e.g., maps, drawings, charts) are reproduced by sectioning the original, beginning at the upper left-hand corner and continuing from left to right in equal sections with small overlaps. Each original is also photographed in one exposure and is included in reduced form at the back of the book. Photographs included in the original manuscript have been reproduced xerographically in this copy. Higher quality 6 " x 9" black and white photographic prints are available for any photographs or illustrations appearing in this copy for an additional charge. Contact UMI directly to order. University Microfilms International A Bell & Howell Information C om pany 300 North Zeeb Road. Ann Arbor. Ml 48106-1346 USA 313/761-4700 800/521-0600 Order Number 9325623 C losed 2 -cell embeddings of 2 -connected graphs in surfaces Zha, Xiaoya, Ph.D. The Ohio State University, 1993 UMI 300 N. ZeebRd. Ann Arbor, MI 48106 C lo sed 2 -cell E m b e d d in g s of 2 -c o n n e c t e d G r a ph s in S urfaces DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Xiaoya Zha, B.S., M.S., The Ohio State University 1993 Dissertation Committee: Approved by Thomas Dowling l Philip Huneke P Adviser Randolph Moses Department of Mathematics Dijen Ray-Chaudhuri Neil Robertson to my wife Qiong Shi, and my parents Binmo Zha and Zhilan Zhou for all they have done through the years ii A cknowledgements I am deeply indebted to my advisor, Dr. Neil Robertson, for his guidance, en­ couragement, many insights and tireless assistance through the preparation of this dissertation. I would like to express my thanks to Dr. Ruth Charney and Dr. Henry Glover, for their valuable help in topology, which has been specially important to this disser­ tation. I am grateful to my committee members Dr. Thomas Dowling, Dr. Philip Huneke, Dr. Randolph Moses and Dr. Dijen K. Ray-Chaudhuri, for their suggestions and the time they have spent reading this dissertation. I would like to express my special appreciation to Qiong Shi, my wife, for her encouragement, faith and many sacrifices, without which this work would have been impossible. Finally, I would like to thank my friend Yining Xia, for many stimulating discus­ sions, help and friendship. V ita August 14, 1959 Born in Tunxi, China. 1982 B.S., Anhui University, Hefei, China. 1984 ..................................M.S., Department of Mathematics, Huazhong University of Science and Technology, Wuhan, China. 1990 ..................................M.S., Department of Mathematics, The Ohio State University, Columbus, Ohio. F ie l d s o f S t u d y Major Field: Mathematics iv T a b l e o f C o n t e n t s ACKNOWLEDGEMENTS ........................................................................................ iii VITA ............................................................................................................................... iv LIST OF FIGURES ..................................................................................................... vii LIST OF TABLES ........................................................................................................ ix INTRODUCTION ........................................................................................................ 1 CHAPTER PAGE I Preliminaries and Survey ..................................................................................... 4 1.1 Preliminaries ............................................................................................... 4 1.2 Survey ............................................................................................................ 10 II The Face Chain M ethod..................................................................................... 20 2.1 Circuit chains and an edge version of face chains .............................. 20 2.2 Vertex version of the face chain m eth o d .............................................. 21 2.3 Two new operations .................................................................................. 26 2.4 Dual circuits and the face attachment model ........................................ 28 2.5 Good face c h a in s ......................................................................................... 30 III Some Topological Results ................................................................................. 41 3.1 Classification of nonseparating simple curves in the Klein bottle . 41 3.2 Homology and homotopy intersections of T and T ~ ........................... 44 3.3 Classification and properties of simple curves in A 3 ........................... 50 IV Closed 2-Cell Embeddings of Lower Surface Embeddable Graphs ............ 57 4.1 R e d u c tio n s ............................................................................................ 57 4.2 Closed 2-cell embeddings of some planar graphs with new edges . 59 4.3 Face chains in the projective plane and the Klein b o ttle .......... 65 4.4 Face chains in ........................................................................................ 70 4.5 Closed 2-cell embeddings of some projective graphs with new edges 76 4.6 Closed 2-cell embeddings of lower surface embeddable graphs . 81 V Minimal Surface Embeddings ........................................................................... 89 5.1 Notation and some technical results .................................................. 90 5.2 A structure theorem ........................................................................... 93 5.3 A pp lication ............................................................................................ 99 5.4 E x a m p le s ............................................................................................... 107 BIBLIOGRAPHY ......................................................................................................... 114 vi L is t o f F ig u r e s 1 24 2 25 3 26 4 27 5 28 6 29 7 30 8 32 9 35 10 37 11 38 12 39 13 42 14 43 15 49 16 51 vii 17 54 18 55 19 56 20 61 21 64 22 66 23 71 24 74 25 75 26 78 27 80 28 94 29 95 30 98 31 99 32 108 33 111 34 112 viii Introduction The closed 2-cell embedding conjecture (called the strong embedding conjecture in [Jae], [LR] and circular embedding conjecture in [RSS]) states that every 2-connected graph G has a closed 2-cell embedding in some surface; i.e., an embedding in a compact closed 2-manifold in which the boundary of each face is a circuit in the graph. This conjecture from the folklore of topological graph theory has been open for at least 30 years. The first result may be due to H. Whitney [Whi] in 1932, who proved that a plane embedding of any 2-connected planar graph is a closed 2-cell embedding. Since then, not much progress has been made. During the last 30 years, topological graph theory has become an active research area which combines graph theory and lower dimensional topology. As a topic of topological graph theory, closed 2-cell embedding has attracted more and more attention. A closed 2-cell embedding can be viewed as a “good” embedding, since embeddings (even genus embeddings) in which the facial walks have repeated vertices and edges may be viewed as “bad” embeddings. Many problems in topological graph theory require “good” embeddings. For instance, it is hard to work with the (surface) dual of an embedded graph if a facial walk has repeated edges because loops will be created. Therefore, if the closed 2-cell embedding conjecture is true, then it will provide a very general class of embeddings of graphs satisfying this useful condition. As an existence 2 problem, it has its own interest as a topic in topological graph theory. On the other hand, for the past 15 years, the topic of cycle double covers of 2- edge-connected graphs has been very active. The cycle double cover conjecture states that every 2 -edge-connected graph has a cycle double cover, i.e. a list of cycles in the graph with each edge in exactly two of these cycles. Part of the reason that this topic has been active is it is related to the well-known 4-color theorem of planar graphs, which was proved in 1974-76 by computer techniques, and to flow theory, including the famous 4-flow and 5-flow conjectures of Tutte. Since the existence of a closed 2- cell embedding of a graph implies the existence of a cycle double cover of that graph, simply by choosing all face boundaries as cycles, research on closed 2 -cell embeddings can also be viewed as a topological approach to the cycle double cover problem. In this dissertation, we try to develop some techniques to approach the closed 2 -cell embedding conjecture and to confirm this conjecture for some classes of graphs. Chapter 1 contains the preliminaries and a survey. In Chapter
Load more

Recommended publications
  • Investigations on Unit Distance Property of Clebsch Graph and Its Complement
    Proceedings of the World Congress on Engineering 2012 Vol I WCE 2012, July 4 - 6, 2012, London, U.K. Investigations on Unit Distance Property of Clebsch Graph and Its Complement Pratima Panigrahi and Uma kant Sahoo ∗yz Abstract|An n-dimensional unit distance graph is on parameters (16,5,0,2) and (16,10,6,6) respectively. a simple graph which can be drawn on n-dimensional These graphs are known to be unique in the respective n Euclidean space R so that its vertices are represented parameters [2]. In this paper we give unit distance n by distinct points in R and edges are represented by representation of Clebsch graph in the 3-dimensional Eu- closed line segments of unit length. In this paper we clidean space R3. Also we show that the complement of show that the Clebsch graph is 3-dimensional unit Clebsch graph is not a 3-dimensional unit distance graph. distance graph, but its complement is not. Keywords: unit distance graph, strongly regular The Petersen graph is the strongly regular graph on graphs, Clebsch graph, Petersen graph. parameters (10,3,0,1). This graph is also unique in its parameter set. It is known that Petersen graph is 2-dimensional unit distance graph (see [1],[3],[10]). It is In this article we consider only simple graphs, i.e. also known that Petersen graph is a subgraph of Clebsch undirected, loop free and with no multiple edges. The graph, see [[5], section 10.6]. study of dimension of graphs was initiated by Erdos et.al [3].
    [Show full text]
  • Directed Cycle Double Cover Conjecture: Fork Graphs
    Directed Cycle Double Cover Conjecture: Fork Graphs Andrea Jim´enez ∗ Martin Loebl y October 22, 2013 Abstract We explore the well-known Jaeger's directed cycle double cover conjecture which is equiva- lent to the assertion that every cubic bridgeless graph has an embedding on a closed orientable surface with no dual loop. We associate each cubic graph G with a novel object H that we call a hexagon graph; perfect matchings of H describe all embeddings of G on closed orientable surfaces. The study of hexagon graphs leads us to define a new class of graphs that we call lean fork-graphs. Fork graphs are cubic bridgeless graphs obtained from a triangle by sequentially connecting fork-type graphs and performing Y−∆, ∆−Y transformations; lean fork-graphs are fork graphs fulfilling a connectivity property. We prove that Jaeger's conjecture holds for the class of lean fork-graphs. The class of lean fork-graphs is rich; namely, for each cubic bridgeless graph G there is a lean fork-graph containing a subdivision of G as an induced subgraph. Our results establish for the first time, to the best of our knowledge, the validity of Jaeger's conjecture in a broad inductively defined class of graphs. 1 Introduction One of the most challenging open problems in graph theory is the cycle double cover conjecture which was independently posed by Szekeres [14] and Seymour [13] in the seventies. It states that every bridgeless graph has a cycle double cover, that is, a system C of cycles such that each edge of the graph belongs to exactly two cycles of C.
    [Show full text]
  • Hydraulic Cylinder Replacement for Cylinders with 3/8” Hydraulic Hose Instructions
    HYDRAULIC CYLINDER REPLACEMENT FOR CYLINDERS WITH 3/8” HYDRAULIC HOSE INSTRUCTIONS INSTALLATION TOOLS: INCLUDED HARDWARE: • Knife or Scizzors A. (1) Hydraulic Cylinder • 5/8” Wrench B. (1) Zip-Tie • 1/2” Wrench • 1/2” Socket & Ratchet IMPORTANT: Pressure MUST be relieved from hydraulic system before proceeding. PRESSURE RELIEF STEP 1: Lower the Power-Pole Anchor® down so the Everflex™ spike is touching the ground. WARNING: Do not touch spike with bare hands. STEP 2: Manually push the anchor into closed position, relieving pressure. Manually lower anchor back to the ground. REMOVAL STEP 1: Remove the Cylinder Bottom from the Upper U-Channel using a 1/2” socket & wrench. FIG 1 or 2 NOTE: For Blade models, push bottom of cylinder up into U-Channel and slide it forward past the Ram Spacers to remove it. Upper U-Channel Upper U-Channel Cylinder Bottom 1/2” Tools 1/2” Tools Ram 1/2” Tools Spacers Cylinder Bottom If Ram-Spacers fall out Older models have (1) long & (1) during removal, push short Ram Spacer. Ram Spacers 1/2” Tools bushings in to hold MUST be installed on the same side Figure 1 Figure 2 them in place. they were removed. Blade Models Pro/Spn Models Need help? Contact our Customer Service Team at 1 + 813.689.9932 Option 2 HYDRAULIC CYLINDER REPLACEMENT FOR CYLINDERS WITH 3/8” HYDRAULIC HOSE INSTRUCTIONS STEP 2: Remove the Cylinder Top from the Lower U-Channel using a 1/2” socket & wrench. FIG 3 or 4 Lower U-Channel Lower U-Channel 1/2” Tools 1/2” Tools Cylinder Top Cylinder Top Figure 3 Figure 4 Blade Models Pro/SPN Models STEP 3: Disconnect the UP Hose from the Hydraulic Cylinder Fitting by holding the 1/2” Wrench 5/8” Wrench Cylinder Fitting Base with a 1/2” wrench and turning the Hydraulic Hose Fitting Cylinder Fitting counter-clockwise with a 5/8” wrench.
    [Show full text]
  • Simple Infinite Presentations for the Mapping Class Group of a Compact
    SIMPLE INFINITE PRESENTATIONS FOR THE MAPPING CLASS GROUP OF A COMPACT NON-ORIENTABLE SURFACE RYOMA KOBAYASHI Abstract. Omori and the author [6] have given an infinite presentation for the mapping class group of a compact non-orientable surface. In this paper, we give more simple infinite presentations for this group. 1. Introduction For g ≥ 1 and n ≥ 0, we denote by Ng,n the closure of a surface obtained by removing disjoint n disks from a connected sum of g real projective planes, and call this surface a compact non-orientable surface of genus g with n boundary components. We can regard Ng,n as a surface obtained by attaching g M¨obius bands to g boundary components of a sphere with g + n boundary components, as shown in Figure 1. We call these attached M¨obius bands crosscaps. Figure 1. A model of a non-orientable surface Ng,n. The mapping class group M(Ng,n) of Ng,n is defined as the group consisting of isotopy classes of all diffeomorphisms of Ng,n which fix the boundary point- wise. M(N1,0) and M(N1,1) are trivial (see [2]). Finite presentations for M(N2,0), M(N2,1), M(N3,0) and M(N4,0) ware given by [9], [1], [14] and [16] respectively. Paris-Szepietowski [13] gave a finite presentation of M(Ng,n) with Dehn twists and arXiv:2009.02843v1 [math.GT] 7 Sep 2020 crosscap transpositions for g + n > 3 with n ≤ 1. Stukow [15] gave another finite presentation of M(Ng,n) with Dehn twists and one crosscap slide for g + n > 3 with n ≤ 1, applying Tietze transformations for the presentation of M(Ng,n) given in [13].
    [Show full text]
  • An Introduction to Topology the Classification Theorem for Surfaces by E
    An Introduction to Topology An Introduction to Topology The Classification theorem for Surfaces By E. C. Zeeman Introduction. The classification theorem is a beautiful example of geometric topology. Although it was discovered in the last century*, yet it manages to convey the spirit of present day research. The proof that we give here is elementary, and its is hoped more intuitive than that found in most textbooks, but in none the less rigorous. It is designed for readers who have never done any topology before. It is the sort of mathematics that could be taught in schools both to foster geometric intuition, and to counteract the present day alarming tendency to drop geometry. It is profound, and yet preserves a sense of fun. In Appendix 1 we explain how a deeper result can be proved if one has available the more sophisticated tools of analytic topology and algebraic topology. Examples. Before starting the theorem let us look at a few examples of surfaces. In any branch of mathematics it is always a good thing to start with examples, because they are the source of our intuition. All the following pictures are of surfaces in 3-dimensions. In example 1 by the word “sphere” we mean just the surface of the sphere, and not the inside. In fact in all the examples we mean just the surface and not the solid inside. 1. Sphere. 2. Torus (or inner tube). 3. Knotted torus. 4. Sphere with knotted torus bored through it. * Zeeman wrote this article in the mid-twentieth century. 1 An Introduction to Topology 5.
    [Show full text]
  • Volumes of Prisms and Cylinders 625
    11-4 11-4 Volumes of Prisms and 11-4 Cylinders 1. Plan Objectives What You’ll Learn Check Skills You’ll Need GO for Help Lessons 1-9 and 10-1 1 To find the volume of a prism 2 To find the volume of • To find the volume of a Find the area of each figure. For answers that are not whole numbers, round to prism a cylinder the nearest tenth. • To find the volume of a 2 Examples cylinder 1. a square with side length 7 cm 49 cm 1 Finding Volume of a 2. a circle with diameter 15 in. 176.7 in.2 . And Why Rectangular Prism 3. a circle with radius 10 mm 314.2 mm2 2 Finding Volume of a To estimate the volume of a 4. a rectangle with length 3 ft and width 1 ft 3 ft2 Triangular Prism backpack, as in Example 4 2 3 Finding Volume of a Cylinder 5. a rectangle with base 14 in. and height 11 in. 154 in. 4 Finding Volume of a 6. a triangle with base 11 cm and height 5 cm 27.5 cm2 Composite Figure 7. an equilateral triangle that is 8 in. on each side 27.7 in.2 New Vocabulary • volume • composite space figure Math Background Integral calculus considers the area under a curve, which leads to computation of volumes of 1 Finding Volume of a Prism solids of revolution. Cavalieri’s Principle is a forerunner of ideas formalized by Newton and Leibniz in calculus. Hands-On Activity: Finding Volume Explore the volume of a prism with unit cubes.
    [Show full text]
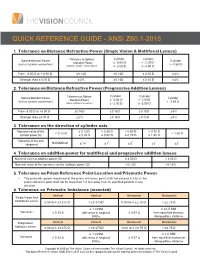
  • Quick Reference Guide - Ansi Z80.1-2015
    QUICK REFERENCE GUIDE - ANSI Z80.1-2015 1. Tolerance on Distance Refractive Power (Single Vision & Multifocal Lenses) Cylinder Cylinder Sphere Meridian Power Tolerance on Sphere Cylinder Meridian Power ≥ 0.00 D > - 2.00 D (minus cylinder convention) > -4.50 D (minus cylinder convention) ≤ -2.00 D ≤ -4.50 D From - 6.50 D to + 6.50 D ± 0.13 D ± 0.13 D ± 0.15 D ± 4% Stronger than ± 6.50 D ± 2% ± 0.13 D ± 0.15 D ± 4% 2. Tolerance on Distance Refractive Power (Progressive Addition Lenses) Cylinder Cylinder Sphere Meridian Power Tolerance on Sphere Cylinder Meridian Power ≥ 0.00 D > - 2.00 D (minus cylinder convention) > -3.50 D (minus cylinder convention) ≤ -2.00 D ≤ -3.50 D From -8.00 D to +8.00 D ± 0.16 D ± 0.16 D ± 0.18 D ± 5% Stronger than ±8.00 D ± 2% ± 0.16 D ± 0.18 D ± 5% 3. Tolerance on the direction of cylinder axis Nominal value of the ≥ 0.12 D > 0.25 D > 0.50 D > 0.75 D < 0.12 D > 1.50 D cylinder power (D) ≤ 0.25 D ≤ 0.50 D ≤ 0.75 D ≤ 1.50 D Tolerance of the axis Not Defined ° ° ° ° ° (degrees) ± 14 ± 7 ± 5 ± 3 ± 2 4. Tolerance on addition power for multifocal and progressive addition lenses Nominal value of addition power (D) ≤ 4.00 D > 4.00 D Nominal value of the tolerance on the addition power (D) ± 0.12 D ± 0.18 D 5. Tolerance on Prism Reference Point Location and Prismatic Power • The prismatic power measured at the prism reference point shall not exceed 0.33Δ or the prism reference point shall not be more than 1.0 mm away from its specified position in any direction.
    [Show full text]
  • Math 7410 Graph Theory
    Math 7410 Graph Theory Bogdan Oporowski Department of Mathematics Louisiana State University April 14, 2021 Definition of a graph Definition 1.1 A graph G is a triple (V,E, I) where ◮ V (or V (G)) is a finite set whose elements are called vertices; ◮ E (or E(G)) is a finite set disjoint from V whose elements are called edges; and ◮ I, called the incidence relation, is a subset of V E in which each edge is × in relation with exactly one or two vertices. v2 e1 v1 Example 1.2 ◮ V = v1, v2, v3, v4 e5 { } e2 e4 ◮ E = e1,e2,e3,e4,e5,e6,e7 { } e6 ◮ I = (v1,e1), (v1,e4), (v1,e5), (v1,e6), { v4 (v2,e1), (v2,e2), (v3,e2), (v3,e3), (v3,e5), e7 v3 e3 (v3,e6), (v4,e3), (v4,e4), (v4,e7) } Simple graphs Definition 1.3 ◮ Edges incident with just one vertex are loops. ◮ Edges incident with the same pair of vertices are parallel. ◮ Graphs with no parallel edges and no loops are called simple. v2 e1 v1 e5 e2 e4 e6 v4 e7 v3 e3 Edges of a simple graph can be described as v e1 v 2 1 two-element subsets of the vertex set. Example 1.4 e5 e2 e4 E = v1, v2 , v2, v3 , v3, v4 , e6 {{ } { } { } v1, v4 , v1, v3 . v4 { } { }} v e7 3 e3 Note 1.5 Graph Terminology Definition 1.6 ◮ The graph G is empty if V = , and is trivial if E = . ∅ ∅ ◮ The cardinality of the vertex-set of a graph G is called the order of G and denoted G .
    [Show full text]
  • A Three-Dimensional Laguerre Geometry and Its Visualization
    A Three-Dimensional Laguerre Geometry and Its Visualization Hans Havlicek and Klaus List, Institut fur¨ Geometrie, TU Wien 3 We describe and visualize the chains of the 3-dimensional chain geometry over the ring R("), " = 0. MSC 2000: 51C05, 53A20. Keywords: chain geometry, Laguerre geometry, affine space, twisted cubic. 1 Introduction The aim of the present paper is to discuss in some detail the Laguerre geometry (cf. [1], [6]) which arises from the 3-dimensional real algebra L := R("), where "3 = 0. This algebra generalizes the algebra of real dual numbers D = R("), where "2 = 0. The Laguerre geometry over D is the geometry on the so-called Blaschke cylinder (Figure 1); the non-degenerate conics on this cylinder are called chains (or cycles, circles). If one generator of the cylinder is removed then the remaining points of the cylinder are in one-one correspon- dence (via a stereographic projection) with the points of the plane of dual numbers, which is an isotropic plane; the chains go over R" to circles and non-isotropic lines. So the point space of the chain geometry over the real dual numbers can be considered as an affine plane with an extra “improper line”. The Laguerre geometry based on L has as point set the projective line P(L) over L. It can be seen as the real affine 3-space on L together with an “improper affine plane”. There is a point model R for this geometry, like the Blaschke cylinder, but it is more compli- cated, and belongs to a 7-dimensional projective space ([6, p.
    [Show full text]
  • On the Cycle Double Cover Problem
    On The Cycle Double Cover Problem Ali Ghassâb1 Dedicated to Prof. E.S. Mahmoodian Abstract In this paper, for each graph , a free edge set is defined. To study the existence of cycle double cover, the naïve cycle double cover of have been defined and studied. In the main theorem, the paper, based on the Kuratowski minor properties, presents a condition to guarantee the existence of a naïve cycle double cover for couple . As a result, the cycle double cover conjecture has been concluded. Moreover, Goddyn’s conjecture - asserting if is a cycle in bridgeless graph , there is a cycle double cover of containing - will have been proved. 1 Ph.D. student at Sharif University of Technology e-mail: [email protected] Faculty of Math, Sharif University of Technology, Tehran, Iran 1 Cycle Double Cover: History, Trends, Advantages A cycle double cover of a graph is a collection of its cycles covering each edge of the graph exactly twice. G. Szekeres in 1973 and, independently, P. Seymour in 1979 conjectured: Conjecture (cycle double cover). Every bridgeless graph has a cycle double cover. Yielded next data are just a glimpse review of the history, trend, and advantages of the research. There are three extremely helpful references: F. Jaeger’s survey article as the oldest one, and M. Chan’s survey article as the newest one. Moreover, C.Q. Zhang’s book as a complete reference illustrating the relative problems and rather new researches on the conjecture. A number of attacks, to prove the conjecture, have been happened. Some of them have built new approaches and trends to study.
    [Show full text]
  • Closed 2-Cell Embeddings of Graphs with No V8-Minors
    Discrete Mathematics 230 (2001) 207–213 www.elsevier.com/locate/disc Closed 2-cell embeddings of graphs with no V8-minors Neil Robertsona;∗;1, Xiaoya Zhab;2 aDepartment of Mathematics, Ohio State University, Columbus, OH 43210, USA bDepartment of Mathematical Sciences, Middle Tennessee State University, Murfreesboro, TN 37132, USA Received 12 July 1996; revised 30 June 1997; accepted 14 October 1999 Abstract A closed 2-cell embedding of a graph embedded in some surface is an embedding such that each face is bounded by a cycle in the graph. The strong embedding conjecture says that every 2-connected graph has a closed 2-cell embedding in some surface. In this paper, we prove that any 2-connected graph without V8 (the Mobius 4-ladder) as a minor has a closed 2-cell embedding in some surface. As a corollary, such a graph has a cycle double cover. The proof uses a classiÿcation of internally-4-connected graphs with no V8-minor (due to Kelmans and independently Robertson), and the proof depends heavily on such a characterization. c 2001 Elsevier Science B.V. All rights reserved. Keywords: Embedding; Strong embedding conjecture; V8 minor; Cycle double cover; Closed 2-cell embedding 1. Introduction The closed 2-cell embedding (called strong embedding in [2,4], and circular em- bedding in [6]) conjecture says that every 2-connected graph G has a closed 2-cell embedding in some surface, that is, an embedding in a compact closed 2-manifold in which each face is simply connected and the boundary of each face is a cycle in the graph (no repeated vertices or edges on the face boundary).
    [Show full text]
  • 1 University of California, Berkeley Physics 7A, Section 1, Spring 2009
    1 University of California, Berkeley Physics 7A, Section 1, Spring 2009 (Yury Kolomensky) SOLUTIONS TO THE SECOND MIDTERM Maximum score: 100 points 1. (10 points) Blitz (a) hoop, disk, sphere This is a set of simple questions to warm you up. The (b) disk, hoop, sphere problem consists of five questions, 2 points each. (c) sphere, hoop, disk 1. Circle correct answer. Imagine a basketball bouncing on a court. After a dozen or so (d) sphere, disk, hoop bounces, the ball stops. From this, you can con- (e) hoop, sphere, disk clude that Answer: (d). The object with highest moment of (a) Energy is not conserved. inertia has the largest kinetic energy at the bot- (b) Mechanical energy is conserved, but only tom, and would reach highest elevation. The ob- for a single bounce. ject with the smallest moment of inertia (sphere) (c) Total energy in conserved, but mechanical will therefore reach lowest altitude, and the ob- energy is transformed into other types of ject with the largest moment of inertia (hoop) energy (e.g. heat). will be highest. (d) Potential energy is transformed into kinetic 4. A particle attached to the end of a massless rod energy of length R is rotating counter-clockwise in the (e) None of the above. horizontal plane with a constant angular velocity ω as shown in the picture below. Answer: (c) 2. Circle correct answer. In an elastic collision ω (a) momentum is not conserved but kinetic en- ergy is conserved; (b) momentum is conserved but kinetic energy R is not conserved; (c) both momentum and kinetic energy are conserved; (d) neither kinetic energy nor momentum is Which direction does the vector ~ω point ? conserved; (e) none of the above.
    [Show full text]