Maximum Likelihood Estimation for Incomplete Multinomial Data Via the Weaver Algorithm
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Modelling Rankings in R: the Plackettluce Package∗
Modelling rankings in R: the PlackettLuce package∗ Heather L. Turnery Jacob van Ettenz David Firthx Ioannis Kosmidis{ December 17, 2019 Abstract This paper presents the R package PlackettLuce, which implements a generalization of the Plackett-Luce model for rankings data. The generalization accommodates both ties (of arbitrary order) and partial rankings (complete rankings of subsets of items). By default, the implementation adds a set of pseudo-comparisons with a hypothetical item, ensuring that the underlying network of wins and losses between items is always strongly connected. In this way, the worth of each item always has a finite maximum likelihood estimate, with finite standard error. The use of pseudo-comparisons also has a regularization effect, shrinking the estimated parameters towards equal item worth. In addition to standard methods for model summary, PlackettLuce provides a method to compute quasi standard errors for the item parameters. This provides the basis for comparison intervals that do not change with the choice of identifiability constraint placed on the item parameters. Finally, the package provides a method for model-based partitioning using covariates whose values vary between rankings, enabling the identification of subgroups of judges or settings with different item worths. The features of the package are demonstrated through application to classic and novel data sets. 1 Introduction Rankings data arise in a range of applications, such as sport tournaments and consumer studies. In rankings data, each observation is an ordering of a set of items. A classic model for such data is the Plackett-Luce model, which stems from Luce’s axiom of choice (Luce, 1959, 1977). -

Modelling Rankings in R: the Plackettluce Package
Computational Statistics (2020) 35:1027–1057 https://doi.org/10.1007/s00180-020-00959-3 ORIGINAL PAPER Modelling rankings in R: the PlackettLuce package Heather L. Turner1 · Jacob van Etten2 · David Firth1,3 · Ioannis Kosmidis1,3 Received: 30 October 2018 / Accepted: 18 January 2020 / Published online: 12 February 2020 © The Author(s) 2020 Abstract This paper presents the R package PlackettLuce, which implements a generalization of the Plackett–Luce model for rankings data. The generalization accommodates both ties (of arbitrary order) and partial rankings (complete rankings of subsets of items). By default, the implementation adds a set of pseudo-comparisons with a hypothetical item, ensuring that the underlying network of wins and losses between items is always strongly connected. In this way, the worth of each item always has a finite maximum likelihood estimate, with finite standard error. The use of pseudo-comparisons also has a regularization effect, shrinking the estimated parameters towards equal item worth. In addition to standard methods for model summary, PlackettLuce provides a method to compute quasi standard errors for the item parameters. This provides the basis for comparison intervals that do not change with the choice of identifiability constraint placed on the item parameters. Finally, the package provides a method for model- based partitioning using covariates whose values vary between rankings, enabling the identification of subgroups of judges or settings with different item worths. The features of the package are demonstrated through application to classic and novel data sets. This research is part of cooperative agreement AID-OAA-F-14-00035, which was made possible by the generous support of the American people through the United States Agency for International Development (USAID). -

1911: All 40 Starters
INDIANAPOLIS 500 – ROOKIES BY YEAR 1911: All 40 starters 1912: (8) Bert Dingley, Joe Horan, Johnny Jenkins, Billy Liesaw, Joe Matson, Len Ormsby, Eddie Rickenbacker, Len Zengel 1913: (10) George Clark, Robert Evans, Jules Goux, Albert Guyot, Willie Haupt, Don Herr, Joe Nikrent, Theodore Pilette, Vincenzo Trucco, Paul Zuccarelli 1914: (15) George Boillot, S.F. Brock, Billy Carlson, Billy Chandler, Jean Chassagne, Josef Christiaens, Earl Cooper, Arthur Duray, Ernst Friedrich, Ray Gilhooly, Charles Keene, Art Klein, George Mason, Barney Oldfield, Rene Thomas 1915: (13) Tom Alley, George Babcock, Louis Chevrolet, Joe Cooper, C.C. Cox, John DePalma, George Hill, Johnny Mais, Eddie O’Donnell, Tom Orr, Jean Porporato, Dario Resta, Noel Van Raalte 1916: (8) Wilbur D’Alene, Jules DeVigne, Aldo Franchi, Ora Haibe, Pete Henderson, Art Johnson, Dave Lewis, Tom Rooney 1919: (19) Paul Bablot, Andre Boillot, Joe Boyer, W.W. Brown, Gaston Chevrolet, Cliff Durant, Denny Hickey, Kurt Hitke, Ray Howard, Charles Kirkpatrick, Louis LeCocq, J.J. McCoy, Tommy Milton, Roscoe Sarles, Elmer Shannon, Arthur Thurman, Omar Toft, Ira Vail, Louis Wagner 1920: (4) John Boling, Bennett Hill, Jimmy Murphy, Joe Thomas 1921: (6) Riley Brett, Jules Ellingboe, Louis Fontaine, Percy Ford, Eddie Miller, C.W. Van Ranst 1922: (11) E.G. “Cannonball” Baker, L.L. Corum, Jack Curtner, Peter DePaolo, Leon Duray, Frank Elliott, I.P Fetterman, Harry Hartz, Douglas Hawkes, Glenn Howard, Jerry Wonderlich 1923: (10) Martin de Alzaga, Prince de Cystria, Pierre de Viscaya, Harlan Fengler, Christian Lautenschlager, Wade Morton, Raoul Riganti, Max Sailer, Christian Werner, Count Louis Zborowski 1924: (7) Ernie Ansterburg, Fred Comer, Fred Harder, Bill Hunt, Bob McDonogh, Alfred E. -

Post-Race Report
Loop Data Statistics Post-Race Report Sylvania 300 September 18, 2005 Provided by STATS LLC and NASCAR - Thursday, January 22, 2009 NASCAR Nextel Cup Series Average Running Position Sum of driver position on each lap - divided by the laps run in the race. Sylvania 300 New Hampshire International Speedway September 18, 2005 Car Finish Average Rk. Number Driver Team Pos. Place 1 20 Tony Stewart The Home Depot 2 2.933 2 12 Ryan Newman Mobil 1/alltel 1 7.263 3 8 Dale Earnhardt Jr. Budweiser 5 7.407 4 17 Matt Kenseth DeWalt 3 7.547 5 24 Jeff Gordon Dupont 14 7.663 6 48 Jimmie Johnson Lowe's 8 9.453 7 29 Kevin Harvick GM Goodwrench 10 9.637 8 31 Jeff Burton Cingular Wireless 9 10.973 9 16 Greg Biffle National Guard 4 11.130 10 19 Jeremy Mayfield Dodge Dealers/UAW 16 11.860 11 6 Mark Martin Viagra 7 12.730 12 38 Elliott Sadler M&M's 30 12.913 13 2 Rusty Wallace Miller Lite 6 13.290 14 25 Brian Vickers GMAC/ditech.com 13 16.363 15 40 Sterling Marlin Coors Light 11 17.240 16 01 Joe Nemechek U.S. Army 25 17.247 17 42 Jamie McMurray Havoline/Texaco 12 17.297 18 21 Ricky Rudd Motorcraft Genuine Parts 20 18.550 19 18 Bobby Labonte Interstate Batteries 24 18.567 20 88 Dale Jarrett UPS 18 18.667 21 5 Kyle Busch Kellogg's 27 18.917 22 15 Michael Waltrip NAPA Auto Parts 15 19.333 23 43 Jeff Green Cheerios/Betty Crocker 17 21.257 24 99 Carl Edwards Office Depot/Scott's 19 22.883 25 41 Casey Mears Target 23 23.407 26 0 Mike Bliss NetZero/Best Buy 36 24.627 27 22 Scott Wimmer Caterpillar 26 25.220 28 9 Kasey Kahne Dodge Dealers/UAW 38 25.813 29 7 Robby Gordon Jim Beam 37 27.153 30 4 Mike Wallace Lucas Oil Products 22 27.307 31 45 Kyle Petty Georgia Pacific/Brawny 21 28.783 32 10 Scott Riggs Valvoline 28 30.517 33 32 Bobby Hamilton Jr. -

NASCAR for Dummies (ISBN
spine=.672” Sports/Motor Sports ™ Making Everything Easier! 3rd Edition Now updated! Your authoritative guide to NASCAR — 3rd Edition on and off the track Open the book and find: ® Want to have the supreme NASCAR experience? Whether • Top driver Mark Martin’s personal NASCAR you’re new to this exciting sport or a longtime fan, this insights into the sport insider’s guide covers everything you want to know in • The lowdown on each NASCAR detail — from the anatomy of a stock car to the strategies track used by top drivers in the NASCAR Sprint Cup Series. • Why drivers are true athletes NASCAR • What’s new with NASCAR? — get the latest on the new racing rules, teams, drivers, car designs, and safety requirements • Explanations of NASCAR lingo • A crash course in stock-car racing — meet the teams and • How to win a race (it’s more than sponsors, understand the different NASCAR series, and find out just driving fast!) how drivers get started in the racing business • What happens during a pit stop • Take a test drive — explore a stock car inside and out, learn the • How to fit in with a NASCAR crowd rules of the track, and work with the race team • Understand the driver’s world — get inside a driver’s head and • Ten can’t-miss races of the year ® see what happens before, during, and after a race • NASCAR statistics, race car • Keep track of NASCAR events — from the stands or the comfort numbers, and milestones of home, follow the sport and get the most out of each race Go to dummies.com® for more! Learn to: • Identify the teams, drivers, and cars • Follow all the latest rules and regulations • Understand the top driver skills and racing strategies • Have the ultimate fan experience, at home or at the track Mark Martin burst onto the NASCAR scene in 1981 $21.99 US / $25.99 CN / £14.99 UK after earning four American Speed Association championships, and has been winning races and ISBN 978-0-470-43068-2 setting records ever since. -

Mike Twedt 4/29 (Woo) Mark K
COMPLETE RESULTS FOR 1988 Date (Sanction/Event) – Winners 4/23 410 – Jerry Richert Jr., 360 – Mike Twedt 4/29 (WoO) Mark Kinser 4/30 (WoO) Steve Kinser 5/7 410 – Sammy Swindell, 360 – David Hesmer 5/14 410 – Jerry Richert Jr., 360 – Dean Chadd 5/21 Rain 5/28 410 – Danny Thoman, 360 – Dwight Snodgrass 6/4 410 – Danny Lasoski, 360 – Rick McClure 6/11 (USAC winged) Sammy Swindell, 360 – Rick McClure 6/18 Rain 6/22 (WoO) Steve Kinser, 360 – Dean Chadd 6/25 410 – Randy Smith, 360 – David Hesmer 7/2 410 – Randy Smith, 360 – Jordan Albaugh 7/9 (Twin Features) 410 – Randy Smith, Danny Young, 360 – David Hesmer, Mike Twedt 7/16 410 – Randy Smith, 360 – Toby Lawless 7/23 410 – Terry McCarl, 360 – Terry Thorson 7/26 (Enduro) Bob Maschman 7/28 (Modified) Brad Dubil 7/29 (WoO Late Models) Billy Moyer 7/30 410 – Danny Lasoski, 360 – Mike Twedt 8/6 410 – Danny Lasoski, 360 – David Hesmer 8/10 (Knoxville Nationals Prelim) Bobby Davis Jr. 8/11 (Knoxville Nationals Prelim) Dave Blaney 8/12 (Knoxville Nationals NQ) Doug Wolfgang, (Race of States) Doug Wolfgang, (Mystery Feature) Sammy Swindell 8/13 (Knoxville Nationals) Steve Kinser 8/27 410 – Randy Smith, 360 – David Hesmer 4/23/88 Weather Cold, Richert Hot at Knoxville Opener by Bob Wilson Knoxville, IA – Jerry Richert Jr., son of 1962 Knoxville Nationals champion, Jerry Richert Sr., captured the 20 lap season opener at the Knoxville Raceway Saturday night. The win, Richert’s initial here, came aboard the Marty Johnson Taggert Racing Gambler and earned $2,000 for the young Minnesota pilot in track record time. -

Kentucky Speedway Arca Records 2000-2015
KENTUCKY SPEEDWAY ARCA RECORDS 2000-2015 CAR PERFORMANCE AT KENTUCKY CAR MAKE ENTRIES WINS RUNNING % RUNNING AVG. PURSE TOTAL PURSE WON Chevrolet 367 2 229 62 NA NA Ford 251 11 166 66 NA NA Dodge 108 6 81 75 NA NA Pontiac 40 0 22 55 NA NA Toyota 43 3 37 86 NA NA TOP FIVE FINISHERS 205-MILE RACES YEAR FIRST (Started) SECOND THIRD FOURTH FIFTH 2004 Ryan Hemphill (2) Billy Venturini Mark Gibson Ken Weaver Christi Passmore 2003 Kyle Busch (4) Frank Kimmel Matt Hagans Shelby Howard Jason Jarrett 200-MILE RACES YEAR FIRST (Started) SECOND THIRD FOURTH FIFTH 2002 Chad Blount (3) Frank Kimmel Austin Cameron Jason Jarrett Mark Gibson 2001 Frank Kimmel (1) John Metcalf Billy Venturini Todd Bowsher Chase Montgomery 2000 Ryan Newman (1) Tim Steele A.J. Henriksen Billy Venturini Bobby Gerhart 155-MILE RACES YEAR FIRST (Started) SECOND THIRD FOURTH FIFTH 2002 Frank Kimmel (2) Chad Blount Jason Rudd John Metcalf Andy Belmont 150-MILE RACES YEAR FIRST (Started) SECOND THIRD FOURTH FIFTH Sept. 26, 2015 Ryan Reed (9) Travis Braden David Levine Ross Kenseth Grant Enfinger Sept. 19, 2014 Brennan Poole (8) Matt Tifft Mason Mitchell Cody Coughlin Daniel Suarez Sept. 21, 2013 Corey Lajoie (13) Mason Mitchell Spencer Grant Enfinger Chad Boat Gallaher 2009 Parker Kligerman (2) Grant Enfinger Justin Lofton Craig Goess Brian Ickler 2009 James Buescher (1) Justin Lofton Jesse Smith Brian Ickler Frank Kimmel 2008 Scott Speed (6) Sean Caisse Justin Allgaier Frank Kimmel Brian Scott 2008 Ricky Stenhouse, Jr. (15) Scott Speed Ryan Fischer Ken Butler III John Wes Townley 2007 Michael McDowell (2) Cale Gale Bobby Santos Alex Yontz Erin Crocker 2007 Erik Darnell (5) Erin Crocker Bobby Santos Scott Lagasse, Chad Blount Jr. -

Points Report Talladega Superspeedway UAW-Ford 500 UNOFFICIAL Provided by NASCAR Statistical Services - Sun, Oct 2, 2005 @ 08:09 PM Eastern UNOFFICIAL
Points Report Talladega Superspeedway UAW-Ford 500 UNOFFICIAL Provided by NASCAR Statistical Services - Sun, Oct 2, 2005 @ 08:09 PM Eastern UNOFFICIAL Pos Driver BPts Points -Ldr -Nxt Starts Poles Wins T5s T10s DNFs Money Won PPos G/L 1 Tony Stewart 120 5519 0 0 29 2 5 14 20 1 $5,829,335 5 4 2 Ryan Newman 80 5515 -4 -4 29 6 1 8 13 3 $4,590,956 3 1 3 Rusty Wallace 35 5443 -76 -72 29 0 0 8 16 0 $4,048,697 2 -1 4 Jimmie Johnson 80 5437 -82 -6 29 1 3 10 17 4 $5,622,476 1 -3 5 Greg Biffle 115 5421 -98 -16 29 0 5 11 16 1 $4,563,902 6 1 6 Carl Edwards 40 5419 -100 -2 29 1 2 9 12 1 $3,512,909 8 2 7 Matt Kenseth 75 5408 -111 -11 29 1 1 8 13 4 $4,595,182 9 2 8 Jeremy Mayfield 50 5407 -112 -1 29 0 1 4 8 1 $3,831,461 7 -1 9 Mark Martin 50 5381 -138 -26 29 0 0 7 14 2 $4,593,193 4 -5 10 Kurt Busch 105 5339 -180 -42 29 0 3 8 15 3 $5,721,366 10 0 11 Kevin Harvick 45 3321 0 0 29 2 1 3 9 1 $4,098,812 12 1 12 Jamie McMurray 10 3307 -14 -14 29 1 0 4 8 3 $3,309,124 13 1 13 Elliott Sadler 55 3288 -33 -19 29 3 0 1 10 2 $4,077,999 11 -2 14 Dale Jarrett 15 3270 -51 -18 29 1 1 4 6 1 $3,859,097 15 1 15 Joe Nemechek 50 3222 -99 -48 29 1 0 1 8 2 $3,437,038 16 1 16 Jeff Gordon 65 3202 -119 -20 29 2 3 5 9 8 $5,686,421 14 -2 17 Brian Vickers 55 3187 -134 -15 29 1 0 5 10 3 $3,363,819 18 1 18 Dale Earnhardt Jr. -

Kasey Kahne Chevy American Revolution 400 – Richmond International Raceway May 13, 2005
Bud Pole Winner: Kasey Kahne Chevy American Revolution 400 – Richmond International Raceway May 13, 2005 • Kasey Kahne won the NASCAR NEXTEL Cup Series Bud Pole for the Chevy American Revolution 400, lapping Richmond International Raceway in 20.775 seconds at 129.964 mph. Brian Vickers holds the track-qualifying record of 20.772 seconds, 129.983 mph, set May 14, 2004. • This is Kahne’s sixth career Bud Pole in 47 NASCAR NEXTEL Cup Series races. His most recent Bud Pole was last week at Darlington. • This is Kahne’s first top-10 start in three NASCAR NEXTEL Cup Series race at Richmond International Raceway. • Kahne, who also won the Busch Pole for the NASCAR Busch Series race later tonight, became the first driver to sweep weekend poles at Richmond. The last driver to sweep both poles in a weekend was Mark Martin at Rockingham in October 1999. • There has been a different Bud Pole winner in each of the past 11 races at Richmond International Raceway. • Ryan Newman posted the second-quickest qualifying lap of 20.801 seconds, 129.801 mph – and will join Kahne on the front row for the Chevy American Revolution 400. Newman has started from a top-10 starting position in each race this season, the only driver to do so. He has also started from the top-10 in six of his seven races at Richmond, including four times from the front row. • This is the fifth Bud Pole for Dodge in 2005. Chevrolet has four Bud Poles and Ford has two. • Tony Stewart (third) posted his sixth top-10 start in 13 races at Richmond, but his first since May 2003. -
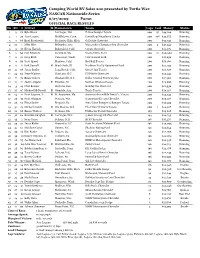
NNS Race Results
Camping World RV Sales 200 presented by Turtle Wax NASCAR Nationwide Series 6/27/2009 Purse: OFFICIAL RACE RESULTS Fn Str # Driver R Hometown Team Laps Led Money Status 1 9 18 Kyle Busch Las Vegas, Nev. Z-Line Designs Toyota 20037 $44,120 Running 2 1 20 Joey Logano Middletown, Conn. GameStop/Singularity Toyota 200108 $39,675 Running 3 7 88 Brad Keselowski Rochester Hills, Mich. GoDaddy Chevrolet 200 $32,743 Running 4 10 1 Mike Bliss Milwaukie, Ore. Miccosukee Championship Chevrolet 2003 $37,043 Running 5 5 33 Kevin Harvick Bakersfield, Calif. Copart Chevrolet 200 $21,475 Running 6 2 60 Carl Edwards Columbia, Mo. Scotts/Ortho Ford 20051 $20,200 Running 7 6 16 Greg Biffle Vancouver, Wash. CitiFinancial Ford 200 $18,650 Running 8 4 99 Scott Speed Manteca, Calif. Red Bull Toyota 200 $18,150 Running 9 11 6 Erik Darnell R Beach Park, Ill. Northern Tool & Equipment Ford 200 $25,193 Running 10 12 38 Jason Leffler Long Beach, Calif. Great Clips Toyota 200 $24,818 Running 11 24 66 Steve Wallace Charlotte, N.C. US Fidelis Chevrolet 200 $23,943 Running 12 8 32 Brian Vickers Thomasville, N.C. Dollar General Stores Toyota 200 $17,350 Running 13 1312 Justin Allgaier R Riverton, Ill. Verizon Wireless Dodge 200 $23,668 Running 14 3 29 Clint Bowyer Emporia, Kan. Holiday Inn Chevrolet 200 $18,930 Running 15 1647 Michael McDowell R Glendale, Ariz. Tom's Toyota 200 $24,118 Running 16 1411 Scott Lagasse, Jr. R St. Augustine, Fla. America's Incredible Pizza Co. -

Post-Race Report
Loop Data Statistics Post-Race Report Batman Begins 400 June 19, 2005 Provided by STATS LLC and NASCAR - Thursday, January 22, 2009 NASCAR Nextel Cup Series Average Running Position Sum of driver position on each lap - divided by the laps run in the race. Batman Begins 400 Michigan International Speedway June 19, 2005 Car Finish Average Rk. Number Driver Team Pos. Place 1 20 Tony Stewart The Home Depot 2 2.485 2 16 Greg Biffle Charter/National Guard 1 4.035 3 97 Kurt Busch Sharpie 12 4.930 4 17 Matt Kenseth Carhartt/Dewalt 4 5.300 5 6 Mark Martin Pfizer/Batman Begins 3 7.680 6 12 Ryan Newman alltel 15 7.725 7 99 Carl Edwards AAA/Office Depot 5 8.270 8 01 Joe Nemechek U.S. Army 6 11.210 9 48 Jimmie Johnson Lowe's 19 12.415 10 18 Bobby Labonte Interstate Batteries 14 12.655 11 15 Michael Waltrip NAPA Auto Parts 7 12.790 12 2 Rusty Wallace Miller Lite 10 13.165 13 41 Casey Mears Target 21 13.955 14 42 Jamie McMurray Home 123/Havoline 13 14.045 15 38 Elliott Sadler M&M's 8 15.120 16 5 Kyle Busch Kellogg's 9 15.140 17 31 Jeff Burton Beneficial/Cingular 11 18.060 18 9 Kasey Kahne Dodge Dealers/UAW 18 18.145 19 22 Scott Wimmer Caterpillar 16 19.440 20 8 Dale Earnhardt Jr. Budweiser 17 21.060 21 19 Jeremy Mayfield Dodge Dealers/UAW 22 21.190 22 40 Sterling Marlin Coors Light 40 22.030 23 10 Scott Riggs Valvoline 23 22.650 24 77 Travis Kvapil Kodak/Jasper Engines 26 24.765 25 88 Dale Jarrett UPS 24 24.835 26 11 Jason Leffler FedEx Kinko's 20 26.085 27 24 Jeff Gordon Dupont 32 27.215 28 29 Kevin Harvick GM Goodwrench 25 27.360 29 0 Mike Bliss NetZero/Best Buy 27 27.720 30 7 Robby Gordon Menard's 39 27.935 31 21 Ricky Rudd Rent-A-Center/Motorcraft 33 28.345 32 45 Kyle Petty Georgia-Pacific/Brawny 30 30.495 33 32 Bobby Hamilton Jr. -

Bud Pole Winner: Elliott Sadler Allstate 400 at the Brickyard – Indianapolis Motor Speedway Aug
Bud Pole Winner: Elliott Sadler AllState 400 at the Brickyard – Indianapolis Motor Speedway Aug. 11, 2005 • Elliot Sadler won the NASCAR NEXTEL Cup Series Bud Pole for the AllState 400 at the Brickyard, lapping Indianapolis Motor Speedway in 48.882 seconds at 184.116 mph. Casey Mears holds the track-qualifying record of 48.311 seconds, 186.293 mph, set Aug. 7, 2004. • This is Sadler’s fourth career Bud Pole in 234 NASCAR NEXTEL Cup Series races. This is his second Bud Pole and 11th top-10 start this season. • This is Sadler’s second top-10 start in seven NASCAR NEXTEL Cup Series race at Indianapolis Motor Speedway. He started third and finished third here in 2004. • Sadler became the fourth repeat Bud Pole winner this season. • Jeremy Mayfield posted the second-quickest qualifying lap of 49.166 seconds, 183.053 mph – and will join Sadler on the front row for the AllState 400 at the Brickyard. He has started from a top-10 starting position in just three of his 11 races at Indianapolis. Mayfield tied his season-best start set at Texas with his ninth top-10 start of 2005. • This is the third Bud Pole for Ford in 2005. Chevrolet has nine Bud Poles and Dodge has eight. Qualifying was canceled at Dover in June. • Michael Waltrip (third) posted his fourth top-10 start in 12 races at Indianapolis. Waltrip posted his third top-10 start in 2005. • Kasey Kahne (fourth) scored his first top-10 start in two races at Indianapolis. Kahne posted his 10th top-10 start in 2005.