Central Asia Railways Telecommunications
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Auksion-TUR 27.11.2020.Pdf
ÜNS BERIŇ! BÄSLEŞIKLI SÖWDA! Türkmenistanyň Maliýe we ykdysadyýet ministrligi Türkmenistanyň döwlet eýeçiligindäki desgalary hususylaşdyrmak hakynda kanunçylygyna laýyklykda, döwlet eýeçiligindäki desgalary satmak boýunça bäsleşikli söwdalaryň geçirilýändigini habar berýär. Bäsleşikli söwdalar 2020-nji ýylyň 27-nji noýabrynda sagat 10-00-da Türkmenistanyň Maliýe we ykdysadyýet ministrliginiň jaýynda geçirilýär. Salgysy: Aşgabat şäheriniň Arçabil şaýolynyň 156-njy jaýy. Bäsleşikli söwdada satuwa çykarylýan Türkmenistanyň Söwda we daşary ykdysady aragatnaşyklar ministrliginiň, Türkmenistanyň Oba hojalyk we daşky gurşawy goramak ministrliginiň, “Türkmengaz” döwlet konserniniň, “Türkmenhaly” döwlet birleşiginiň, Aşgabat şäheriniň we Ahal, Daşoguz, Lebap hem-de Mary welaýat häkimlikleriniň desgalarynyň sanawy. Desganyň görnüşi, Binalaryň Başlangyç Hususylaşdyrma Desgalaryň ady, № (işiniň ugry, gurlan meýdany, bahasy gyň ýerleşýän ýeri ýyly) (m²) (manat) şertleri Türkmenistanyň Söwda we daşary ykdysady aragatnaşyklar ministrliginiň desgalary Balkan welaýaty Balkan welaýat Alyjylar jemgyýetleri birleşiginiň Esenguly etrap Söwda işleri, Hususy eýeçilige 1 Alyjylar jemgyýetiniň Söwda merkezi, Esenguly etrabynyň Esenguly 737,80 1 037 362,90 2008ý. satmak şäheri. Balkan welaýat Alyjylar jemgyýetleri birleşiginiň Serdar etrap Alyjylar Ammar, Hususy eýeçilige 2 jemgyýetine degişli Ammar binasy, Serdar şäheriniň G.Meretjäýew 578,80 89 024,40 1979ý. satmak köçesiniň 9-njy jaýy. Balkan welaýat Alyjylar jemgyýetleri birleşiginiň Bereket etrap Jemgyýetçilik iýmiti, Hususy eýeçilige 3 Alyjylar jemgyýetiniň “Gülüstan” restorany, Bereket şäheriniň 1000,10 302 536,80 1976-2008ý. satmak H.Babaýew köçesi. Lebap welaýaty «Lebap» döwlet lomaý-bölek söwda firmasynyň Söwda merkezi, Söwda işleri, Hususy eýeçilige 4 569,00 35 130,00 Gazojak şäheriniň «Sazakino» demir ýol bekedi. 1978ý. satmak Lebap welaýat Alyjylar jemgyýetleri birleşiginiň Köýtendag etrap Söwda işleri, Hususy eýeçilige 5 alyjylar jemgyýetiniň Bazarly söwda merkezi, Köýtendag etrabynyň 632,90 1 787 889,60 2013ý. -
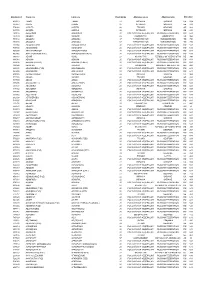
FÁK Állomáskódok
Állomáskód Orosz név Latin név Vasút kódja Államnév orosz Államnév latin Államkód 406513 1 МАЯ 1 MAIA 22 УКРАИНА UKRAINE UA 804 085827 ААКРЕ AAKRE 26 ЭСТОНИЯ ESTONIA EE 233 574066 ААПСТА AAPSTA 28 ГРУЗИЯ GEORGIA GE 268 085780 ААРДЛА AARDLA 26 ЭСТОНИЯ ESTONIA EE 233 269116 АБАБКОВО ABABKOVO 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 737139 АБАДАН ABADAN 29 УЗБЕКИСТАН UZBEKISTAN UZ 860 753112 АБАДАН-I ABADAN-I 67 ТУРКМЕНИСТАН TURKMENISTAN TM 795 753108 АБАДАН-II ABADAN-II 67 ТУРКМЕНИСТАН TURKMENISTAN TM 795 535004 АБАДЗЕХСКАЯ ABADZEHSKAIA 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 795736 АБАЕВСКИЙ ABAEVSKII 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 864300 АБАГУР-ЛЕСНОЙ ABAGUR-LESNOI 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 865065 АБАГУРОВСКИЙ (РЗД) ABAGUROVSKII (RZD) 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 699767 АБАИЛ ABAIL 27 КАЗАХСТАН REPUBLIC OF KAZAKHSTAN KZ 398 888004 АБАКАН ABAKAN 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 888108 АБАКАН (ПЕРЕВ.) ABAKAN (PEREV.) 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 398904 АБАКЛИЯ ABAKLIIA 23 МОЛДАВИЯ MOLDOVA, REPUBLIC OF MD 498 889401 АБАКУМОВКА (РЗД) ABAKUMOVKA 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 882309 АБАЛАКОВО ABALAKOVO 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 408006 АБАМЕЛИКОВО ABAMELIKOVO 22 УКРАИНА UKRAINE UA 804 571706 АБАША ABASHA 28 ГРУЗИЯ GEORGIA GE 268 887500 АБАЗА ABAZA 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 887406 АБАЗА (ЭКСП.) ABAZA (EKSP.) 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 -

Iqtisodiy Geografiya Fanlaridan Test Savollari
OZBEKISTON RESPUBLIKASI XALQ TA’LIMI VAZIRLIGI NAVOIY DAVLAT PEDAGOGIKA INSTITUTI GEOGRAFIYA KAFEDRASI IQTISODIY GEOGRAFIYA FANLARIDAN TEST SAVOLLARI NAVOIY -2008 1 Tuzuvchilar: g.f.n., dots. B.H.Kalonov kat.o`qit. Z.A.Abdiyeva kat.o`qit. M.M.Qodirova o`qit. Sh.Sh.Norov Taqrizchilar: g.f.n.,dots.Yu.B.Raxmatov i.f.n., dots. Z.X.Zoirov Mas’ul muharrir: g.f.n., dots. B.H.Kalonov Tabiatshunoslik fakulteti ilmiy-uslubiy kengashi tomonidan nashrga tavsiya etilgan. 2 SO`Z BOSHI Mazkur test savollari to`plami talabalar bilimini test asosida baholashga qaratilgan. Mamlakatmizda “Ta’lim to`grisida” qonun va “Kadrlar tayyorlash milliy dasturi”ni hayotga tadbiq etish maqsadida oliy ta’lim tizimida juda katta o`zgarishlar amalga oshirildi. Kadrlar tayyorlash Milliy dasturining asosiy talablaridan biri, yangi iqtisodiy – ijtimoiy munosabatlarga to`la javob beruvchi, bozor iqtisodiyoti sharoitida raqobatga bardosh bera oladigan, Vatanga sodiq va fidoiy kadrlarni tayyorlash hisoblanadi. Bunday kadrlarni tarbiyalab etishtirish oliy o`quv yurtlari oldiga yangicha mazmunga ega bo`lgan vazifalarni amalga oshirishni va birinchi navbatda o`quv jarayonini tashkil etishda yangi shakl va uslublarni tadbiq qilishni talab qiladi. Ana shu maqsadda 5440500-Geografiya, 5140500-Geografiya va iqtisodiy bilim asoslari ta’lim yo`nalishlarining o`quv rejasida iqtisodiy geografiya fanlari tizimiga kiruvchi “Sanoat va qishloq xo`jaligi asoslari”, “Aholi geografiyasi va demografiya asoslari”, “Jahon mamlakatlarining iqtisodiy va ijtimoiy geografiyasi”, “O`rta Osiyo iqtisodiy va ijtimoiy geografiyasi”, “O`zbekiston iqtisodiy va ijtimoiy geografiyasi” va “Geografiya o`qitish metodikasi” fanlaridan tuzilgan. Test savollari har bir fandan 50 tadan savollardan va III-variantdan iborat. Savollar oliy maktab fan dasturida berilgan mavzular bo`yicha tuzilgan. -

Water Resources Lifeblood of the Region
Water Resources Lifeblood of the Region 68 Central Asia Atlas of Natural Resources ater has long been the fundamental helped the region flourish; on the other, water, concern of Central Asia’s air, land, and biodiversity have been degraded. peoples. Few parts of the region are naturally water endowed, In this chapter, major river basins, inland seas, Wand it is unevenly distributed geographically. lakes, and reservoirs of Central Asia are presented. This scarcity has caused people to adapt in both The substantial economic and ecological benefits positive and negative ways. Vast power projects they provide are described, along with the threats and irrigation schemes have diverted most of facing them—and consequently the threats the water flow, transforming terrain, ecology, facing the economies and ecology of the country and even climate. On the one hand, powerful themselves—as a result of human activities. electrical grids and rich agricultural areas have The Amu Darya River in Karakalpakstan, Uzbekistan, with a canal (left) taking water to irrigate cotton fields.Upper right: Irrigation lifeline, Dostyk main canal in Makktaaral Rayon in South Kasakhstan Oblast, Kazakhstan. Lower right: The Charyn River in the Balkhash Lake basin, Kazakhstan. Water Resources 69 55°0'E 75°0'E 70 1:10 000 000 Central AsiaAtlas ofNaturalResources Major River Basins in Central Asia 200100 0 200 N Kilometers RUSSIAN FEDERATION 50°0'N Irty sh im 50°0'N Ish ASTANA N ura a b m Lake Zaisan E U r a KAZAKHSTAN l u s y r a S Lake Balkhash PEOPLE’S REPUBLIC Ili OF CHINA Chui Aral Sea National capital 1 International boundary S y r D a r Rivers and canals y a River basins Lake Caspian Sea BISHKEK Issyk-Kul Amu Darya UZBEKISTAN Balkhash-Alakol 40°0'N ryn KYRGYZ Na Ob-Irtysh TASHKENT REPUBLIC Syr Darya 40°0'N Ural 1 Chui-Talas AZERBAIJAN 2 Zarafshan TURKMENISTAN 2 Boundaries are not necessarily authoritative. -

Central Asian Rewiew. Vol. III. No. 1. 1955. Ebook 2016
CENTRAL ASIAN REVIEW A quarterly review of current developments in Soviet Central Asia and Kazakhstan. The area covered in this Review embraces the five S.S R. of Uzbekistan, Tadzhikistan, Kirgizia, Turkmenistan and Kazakhstan. According to Soviet classification “ Central Asia" (Srednyaya Aziya) comprises only the first four of these, Kazakhstan being regarded as a separate area. Issued by the Central Asian Research Centre in association with St. Antony's College (Oxford) Soviet Affairs Study Group. PRICE : SEVEN SHILLINGS & SIXPENCE Vol. III. No. 1. 1955. CENTRAL A sian Re v ie w and other papers issued by the Central Asian Research Centre are under the general editorship of Geoffrey Wheeler, 66 King's Road, London, S.W.3 and David Footman, St. Antony's College, Oxford. CENTRAL A sian Re v ie w aims at presenting a coherent and objective picture of current developments in the five Soviet Socialist Republics of Uzbekistan, Tadzhikistan, Kirgizia, Turkmenistan and Kazakhstan as these are reflected in Soviet publications. The subscription rate is Thirty Shillings per year, post free. The price of single copies is Seven Shillings and Sixpence. Distribution Agents: Messrs. Luzac & Co. Ltd., 46, Great Russell Street, LONDON W.C.1. CENTRAL ASIAN REVIEW CONTENTS Page Industry Thirty Years of Industrial Development in Turkmenistan 1 Sredazneft : Central Asian Oil Authority 8 Central Asian Fisheries 14 Communications Bail ways and Waterways in Kirgizia 20 Agriculture Silk : A Traditional Industry 26 Life on the New Lands of Kazakhstan 32 Economics Central Asian Budget Debates and Plans 37 Public Services Health Services in Central Asia 45 Electric Power in Kazakhstan 55 Archaeology 1953 Expeditions in Kirgizia 61 Cultural Affairs Higher Education in Uzbekistan 68 Islamic Studies in Russia : Part II 76 Vq|. -

Revision of the Quedius Fauna of Middle Asia (Coleoptera, Staphylinidae, Staphylininae)
Dtsch. Entomol. Z. 65 (2) 2018, 117–159 | DOI 10.3897/dez.65.27033 Revision of the Quedius fauna of Middle Asia (Coleoptera, Staphylinidae, Staphylininae) Maria Salnitska1, Alexey Solodovnikov2 1 Department of Entomology, St. Petersburg State University, Universitetskaya Embankment 7/9, Saint-Petersburg, Russia 2 Natural History Museum of Denmark, Zoological Museum, Universitetsparken 15, Copenhagen 2100 Denmark http://zoobank.org/B1A8523C-A463-4FC4-A0C3-072C2E78BA02 Corresponding authors: Maria Salnitska ([email protected]); Alexey Solodovnikov ([email protected]) Abstract Received 29 May 2018 Accepted 6 July 2018 Twenty eight species of the genus Quedius from Middle Asia comprising Kazakhstan, Published 31 July 2018 Kyrgyzstan, Tajikistan, Turkmenistan and Uzbekistan, are revised. Quedius altaicus Korge, 1962, Q. capitalis Eppelsheim, 1892, Q. fusicornis Luze, 1904, Q. solskyi Luze, Academic editor: 1904 and Q. cohaesus Eppelsheim, 1888 are redescribed. The following new synonymies James Liebherr are established: Q. solskyi Luze, 1904 = Q. asiaticus Bernhauer, 1918, syn. n.; Q. cohae- sus Eppelsheim, 1888 = Q. turkmenicus Coiffait, 1969, syn. n., = Q. afghanicus Coiffait, 1977, syn. n.; Q. hauseri Bernhauer, 1918 = Q. peneckei Bernhauer, 1918, syn. n., = Q. Key Words ouzbekiscus Coiffait, 1969,syn. n.; Q. imitator Luze, 1904 = Q. tschinganensis Coiffait, 1969, syn. n.; Q. novus Eppelsheim, 1892 = Q. dzambulensis Coiffait, 1967, syn. n., Staphylininae Q. pseudonigriceps Reitter, 1909 = Q. kirklarensis Korge, 1971, syn. n. Lectotypes are Staphylinini designated for Q. asiaticus Bernhauer, 1918, Q. fusicornis Luze, 1904, Q. hauseri Ber- Quedius nhauer, 1918, Q. imitator Luze, 1904, Q. novus Eppelsheim, 1892 and Q. solskyi Luze, Middle Asia 1904. For all revised species, taxonomy, distribution and bionomics are summarized. -

Uzbekistan Page 1 of 29
2009 Human Rights Report: Uzbekistan Page 1 of 29 Home » Under Secretary for Democracy and Global Affairs » Bureau of Democracy, Human Rights, and Labor » Releases » Human Rights Reports » 2009 Country Reports on Human Rights Practices » South and Central Asia » Uzbekistan 2009 Human Rights Report: Uzbekistan BUREAU OF DEMOCRACY, HUMAN RIGHTS, AND LABOR 2009 Country Reports on Human Rights Practices March 11, 2010 Uzbekistan is an authoritarian state with a population of approximately 27.6 million. The constitution provides for a presidential system with separation of powers among the executive, legislative, and judicial branches. In practice President Islam Karimov and the centralized executive branch dominated political life and exercised nearly complete control over the other branches. Of the 150 members of the lower house of parliament, 135 are elected, and 84 of the 100 senators are chosen in limited elections open only to elected members of local councils. The president appoints the remainder. In December 2007, the country elected President Karimov to a third term in office; however, according to the limited observer mission from the Organization for Security and Cooperation in Europe (OSCE), the government deprived voters of a genuine choice. Parliamentary elections took place on December 27. While noticeable procedural improvements were observed, the elections were not considered free and fair due to government restrictions on eligible candidates and government control of media and campaign financing. Civilian authorities generally -

Turkmenistan – Making the Most of Desert Resources
Turkmenistan Making the Most of Desert Resources urkmen hospitality is legendary, its roots There is little forested land. In fact, four-fifths of the in the distant past. Beyond the traditional country’s surface is desert—most of it the Karakum Khosh geldiniz (welcome), a host’s sacred (Garagum in Turkmen, the official language). And duty has always been to be hospitable to most of the remaining 20% of land is occupied Tguests, even if they are strangers. The hardship of by steep mountains. At the southwest edge of the life and travel in the desert that makes up most of Karakum, the Kopet-Dag Range rises up along the country is such that finding a friendly refuge Turkmenistan’s southern border. This range forms could be a matter of life or death. Inhospitality to a part of the Trans-Eurasian seismic belt, which is traveler is virtually unthinkable. unstable and has caused violent earthquakes in the country. An Uncompromising Terrain Turkmenistan’s most important river is the Amu Darya, the longest river in Central Asia, which Turkmenistan, the second largest Central Asian emanates from the Pamir mountains and flows country, covers 488,100 square kilometers, northwesterly through Turkmenistan. Much of its measuring about 1,100 kilometers from east to water is diverted to the west for irrigation via the west and 650 kilometers from north to south, Karakum Canal. Other major rivers are the Tejen, Upper: The Yangkala Canyon in northwestern Turkmenistan. Lower: The between the Caspian Sea in the west and the the Murgab, and the Atrek. Mausoleum of Turkmenbashi in Ahal Amu Darya River in the east. -

Investor Guide ‘19
INVESTOR GUIDE ‘19 IN ASSOCIATION WITH GOVERNMENT REGIONAL CENTER OF ALMATY REGION FOR DEVELOPMENT OF ALMATY REGION Dear friends! One of the key factors of investment attractiveness is macroeconomic, social and political stability. Almaty region is one of the largest regions in Kazakhstan with huge natural potential and a favorable geographical position for transit opportunities, which provides sufficient possibilities for partnership and business development. All the necessary conditions for the implementation of joint business initiatives with domestic and foreign partners are provided. We are interested in building mutually beneficial relations, in attracting innovative projects using the latest accomplishments and effective technologies. Sincerely, the Governor of Almaty region Amandyk Batalov ALMATY REGION East Kazakhstan region Alakol Karagandy lake region e Sarkand district Alakol district Balkhash lak Karatal Aksu district district Balkhash Eskeldy district TALDYKORGAN district China TEKELI Koksu district Panfilov Ile Kerbulak district district district Kapshagay lake Zhambyl Uigur KAPSHAGAY district region Enbekshikazakh district Zhambyl ALMATY district Talgar Kegen Raimbek district dictrict district Karasay district Kyrgyzstan Area Structure Lakes 223 911 km² 17 districts Balkhash - 16 400 km² 3 cities Alakol - 2 200 km² Population Regional Center Major rivers 2 mln. people Taldykorgan Ili, Aksu, Koksu, Lepsy, Karatal TRANSIT POTENTIAL ТРАНЗИТНЫЙ ПОТЕНЦИАЛ Almaty region has a unique transport and logistics potential: 5 road crossing -

Uzbek: War, Friendship of the Peoples, and the Creation of Soviet Uzbekistan, 1941-1945
Making Ivan-Uzbek: War, Friendship of the Peoples, and the Creation of Soviet Uzbekistan, 1941-1945 By Charles David Shaw A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in History in the Graduate Division of the University of California, Berkeley Committee in charge: Professor Yuri Slezkine, Chair Professor Victoria Frede-Montemayor Professor Victoria E. Bonnell Summer 2015 Abstract Making Ivan-Uzbek: War, Friendship of the Peoples, and the Creation of Soviet Uzbekistan, 1941-1945 by Charles David Shaw Doctor of Philosophy in History University of California, Berkeley Professor Yuri Slezkine, Chair This dissertation addresses the impact of World War II on Uzbek society and contends that the war era should be seen as seen as equally transformative to the tumultuous 1920s and 1930s for Soviet Central Asia. It argues that via the processes of military service, labor mobilization, and the evacuation of Soviet elites and common citizens that Uzbeks joined the broader “Soviet people” or sovetskii narod and overcame the prejudices of being “formerly backward” in Marxist ideology. The dissertation argues that the army was a flexible institution that both catered to national cultural (including Islamic ritual) and linguistic difference but also offered avenues for assimilation to become Ivan-Uzbeks, part of a Russian-speaking, pan-Soviet community of victors. Yet as the war wound down the reemergence of tradition and violence against women made clear the limits of this integration. The dissertation contends that the war shaped the contours of Central Asian society that endured through 1991 and created the basis for thinking of the “Soviet people” as a nation in the 1950s and 1960s. -

List of Districts of Uzbekistan
Karakalpakstan SNo District name District capital 1 Amudaryo District Mang'it 2 Beruniy District Beruniy 3 Chimboy District Chimboy 4 Ellikqala District Bo'ston 5 Kegeyli District* Kegeyli 6 Mo'ynoq District Mo'ynoq 7 Nukus District Oqmang'it 8 Qonliko'l District Qanliko'l 9 Qo'ng'irot District Qo'ng'irot 10 Qorao'zak District Qorao'zak 11 Shumanay District Shumanay 12 Taxtako'pir District Taxtako'pir 13 To'rtko'l District To'rtko'l 14 Xo'jayli District Xo'jayli Xorazm SNo District name District capital 1 Bog'ot District Bog'ot 2 Gurlen District Gurlen 3 Xonqa District Xonqa 4 Xazorasp District Xazorasp 5 Khiva District Khiva 6 Qo'shko'pir District Qo'shko'pir 7 Shovot District Shovot 8 Urganch District Qorovul 9 Yangiariq District Yangiariq 10 Yangibozor District Yangibozor Navoiy SNo District name District capital 1 Kanimekh District Kanimekh 2 Karmana District Navoiy 3 Kyzyltepa District Kyzyltepa 4 Khatyrchi District Yangirabad 5 Navbakhor District Beshrabot 6 Nurata District Nurata 7 Tamdy District Tamdibulok 8 Uchkuduk District Uchkuduk Bukhara SNo District name District capital 1 Alat District Alat 2 Bukhara District Galaasiya 3 Gijduvan District Gijduvan 4 Jondor District Jondor 5 Kagan District Kagan 6 Karakul District Qorako'l 7 Karaulbazar District Karaulbazar 8 Peshku District Yangibazar 9 Romitan District Romitan 10 Shafirkan District Shafirkan 11 Vabkent District Vabkent Samarqand SNo District name District capital 1 Bulungur District Bulungur 2 Ishtikhon District Ishtikhon 3 Jomboy District Jomboy 4 Kattakurgan District -

Report of Expedition to Uzbekistan in 1997
+" ..s::: 11'1 c IJ "t:I OJ ... s:: ro ro E OJ +".... 11'1 ... OJ OJ 10 ..s::: Q. cr::: ..... Report of expedition OJ s:: OJ 0 0 Z to Uzbekistan in 1997 ..s::: +" IJ OJ ....U :::s ..s::: 10 "t:I I- OJ • 0 11'1 Itinerary, collected materials V'l "- OJ OJ c.. IJ cr::: OJ ... and data cr::: :::s 10 0 .... "t:I 11'1 :::s s:: OJ +" ro cr::: :::::l U CI IJ .... .s:: ..... Louis J. M. van Soest CI "t:I- OJ OJ s:: « OJ OJ ... \!) co ... +"s:: 0 ro OJ Q. -"- cpro-dlo ..... ... s:: 0 OJ U -...OJ +"s:: OJ U -- ---. --- -- - ----,- -,--.- . ------- Report of expedition to Uzbekistan in 1997 Itinerary, collected materials and data Louis J.M. van Soest Members collecting teClm: Dr K. I. BClimatov (Uz-NIIR, Uzbekistan) Dr.V.F. Chapurin (VIR, Russia) Dr. AP. Pimakov (Uz-NIIR, Uzbekistan) Agricultural Research Department Centre for Plant Breeding and Reproduction Research (CPRO-DLO) . Centre for Genetic Resources, The Netherlands (CGN) P.O. Box 16 6700 AA Wageningen The Netherlands Tel: +31317477000 Fax: +31' 317 41 80 94 E-mail: [email protected] ------------------- Foreword This report gives an overview of the itinerary and the details of materials and data obtained during a joint multi-crop collecting expedition of the Uzbekistan Research Institute of Plant Industry, the Vavilov Institute of Plant Industry and the Centre for Genetic Resources, the Netherlands, of CPRO-DLO. The joint efforts and commitment of these three institutes and the tenacity of its staff members involved rendered the expedition possible and made it into an important success.