DOCSLIB.ORG

AAO 2016 Telescopes Bailey.Pptx

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
AAO 2016 Telescopes Bailey.Pptx 1/29/16 UNDERSTANDING LOW VISION TELESCOPES Applications for Telescopes in Low Vision Basic and Advanced Observation tasks from audience Theater Ballet Movies Sports Classroom, Public speakers TV in communal environments Ian L Bailey OD, MS, DSc, FCOptom, FAAO School of Optometry General tasks Scenery University of California, Berkeley Faces Cars [email protected] McDonalds Menu Computer screens Mobility tasks Top shelf items Traffic signals Street signs Please silence all mobile devices. Bus numbers, airport signs Unauthorized recording of this Building directories, wall signs session is prohibited. Checking traffic Choices For the Clinician Course Outline or the Patient Review of basic theory Optical Factors Afocal telescopes Magnification Focal telescopes for ametropia or close focus Field size Exit pupil size or entrance pupil for stars Apertures and Stops Adjustable focus/fixed focus Image brightness Range of focusing (for near and ametropia) Field of View and Field of Fixation Can you include astigmatic Rx ? Design Features Image quality Binocular/Monocular Vergence amplification Lens Coatings Hand-held /Head mounted If head mounted Bi-optic ? Practical implications Practical Considerations Tripod/monopod Checking magnification Eye-cup, Objective shroud Measuring BVP Cost Durability Neck, wrist strap, handle Fitting bioptic telescopes Portability (weight/bulk/holder) Influenced by frequency of use Ease of use (mechanical ergonomics) (Protracted, Intermittent, Occasional) Emerging technologies zoom, autofocus, video Cosmesis (conspicuity and perceived acceptability) How do afocal telescopes work? Parallel rays in gives parallel rays out GALILEAN TELESCOPES GALILEAN TELESCOPE Objective Pobj (+/-) A converging element (Convex lens, Concave mirror) P forms a real inverted image. oc Weak objective- long focal length - larger inverted image w w w' Ocular or Eyepiece I Objective’s image must be at primary focal plane of ocular Stronger ocular - short focal length - large image (infinity) f'obj f oc Bailey AAO 2016 1 1/29/16 Image Inversion in Keplerian telescopes KEPLERIAN TELESCOPES KEPLERIAN TELESCOPE Pobj (+/+) Poc w w' w I w' Pechan-Schmidt Porro Prism System Roof Prism System pair of right-angled prisms A Prism A 112.5-45-22.5 f' Prism B 45-62.5-62.5 obj f oc Total internal reflection with 45-90-45 roof so no mirrored surfaces Mirrored surface at 45 deg 45-90-45 45-90-45 Comparing Galilean and Keplerian FOUR BASIC TELESCOPE FORMULAE GALILEAN KEPLERIAN The two obvious relationships Optical path length Short Long Ratio Ocular / Objective Mts = - Poc/ Pobj Image Erect (M=+ve) Inverted (M= -ve) Prisms No Yes Makes it terrestrial d = (1 / Pobj) + (1 / Poc) Sum of focal lengths Ocular Single lens 2 or more lenses Optical surfaces 4 10 or more Two similar formulae (similar to spectacle magnification formula) Exit pupil inside outside M = 1 / (1 - dP ) ts obj Field of view smaller larger Field limits tapered sharp outline M = 1 - d P ts oc Image quality poorer better EQUIVALENT VIEWING DISTANCE 6.3cm AFOCAL TELESCOPES 12.5cm25cm 50cm 2X EVD=12.5cm 100cm AFOCAL iF Parallel rays in give Parallel Rays out EVD=25cm 4X Afocal telescopes have some mathema3cally sweet proper3es EVD=6.3cm EVD=50cm EVD=12.5cm Usually telescopes not quite afocal Objects not at infinity 8X Pa3ents o?en do not want or demand image at infinity EVD=3.2cm EVD=25cm EVD=6.3cm EVD = Viewing distance Enlargement ratio EVD=12.5cm Bailey AAO 2016 2 1/29/16 Adapting Afocal Telescopes (a) POWER CHANGE AT OCULAR for Ametropia Simple and intuitive Hold afocal telescope against own spectacle lens Assume object at infinity OR What can you change? Change ocular lens by adding spectacle Rx (a) OCULAR Place ocular against spec Rx OR Change ocular to include spec Rx Magnification gain = magnification of original telescope (b) LENGTH Change length, changes exit vergence Total magnification = (Spectacle mag) (Telescope mag) No differences for Galilean/Keplerian (c) OBJECTIVE Low Powered Lens Cap OR power change at objective changes exit vergence RARELY USED EVD = viewing distance / Mts FOR HYPEROPE Increase length (b) CHANGE LENGTH Re-assign PLUS power from ocular to provide Rx. Changing length, changes exiting vergence Keplerian telescope Borrow plus from ocular Weaker ocular, longer TS Increasing length adds plus (HYPEROPE) Reduced magnification Also increase length to focus for near (adding plus) Galilean telescope Borrow plus from ocular Decreasing length adds minus (MYOPE) Stronger ocular, longer TS Increased magnification Be able to calculate TS length and Mts FOR MYOPE Decrease length TELESCOPES FOR NEAR VISION Re-assign MINUS power from ocular to provide Rx. 1 Afocal TS with a cap Keplerian telescope EVD = u/M = f /M Borrow minus from ocular ts cap ts Stronger ocular, shorter TS 2. Adjust TS length of afocal telescope Increased magnification EVD = (u/M ) – f EVD ≈ u/Mts ts oc Where foc = focal length of ocular (usually 1-2 cm) Galilean telescope Borrow minus from ocular 3. Afocal telescope over a high add Weaker ocular, shorter TS Rarely used Reduced magnification EVD = Mts . fadd Working distance = M2 f - dM add ts System gives low magnification Long EVD and much longer WD Be able to calculate TS length and Mts Bailey AAO 2016 3 1/29/16 Increasing length Labeling Telescopes a 4x12 TS focused for 20 cm Increase length to 4x12 Monocular telescope M= -100/25 = -4x Two numbers “add plus” for +25 D mm near vision focus. +100 D Magnification x Objective diameter Manufacturers never state negative magnification for Keplerian TS’s 4 cm 1 cm Tube length = 5 cm when afocal 4x12 Effectively borrow is a 4x TS, with objective 12 mm in diameter +5D from objective Adjusted to focus on 20 cm Now system is like a 5x TS with a +5D cap M= -100/20 = -5x Light diverging +20 D 10x50 System behaves like from 20cm +100 D is a 10x TS with objective 50 mm in diameter an afocal telescope 5 cm with a cap on the 1 cm +5D Tube length now 6 cm objective EVD = 20 cm/5x = 4 cm EVP = 25D EXIT PUPILS OBJECTIVE EXIT PUPIL OF KEPLERIAN TELESCOPE Aobj = diam Small images oF ObjecMve lens EYEPIECE A = diam oc Located quite close to eyepiece lens A'obj = Aobj / M ts Keplerian telescopes ( Exit pupil outside TS) Galilean telescopes ( Exit pupil outside TS) Relevant to Image Brightness EXIT PUPIL = image of objective fobj ' foc d Relevant to Field oF View - d / M ts Can help understand imaging by telescopes Exit pupil is a real image suspended in space An important reFerence point Its size is Aobj / M ts It is located d / Mts from the eyepiece lens Can be used to determine magnificaon oF TS OBJECTIVE EXIT PUPIL OF GALILEAN TELESCOPE Image Brightness and Telescopes A = diam obj EYEPIECE A' = A / M obj obj ts A = diam oc REFLECTIONS AND ABSORPTION F All telescopes reduce brightness of real objects EXIT PUPIL = image of objective Light loss (about 15-40%) from reflections f f ' oc from internal optical surfaces obj d Keplerian more light loss - d / M ts More surfaces (compound eyepiece and prisms) Surface coatings reduce light loss Exit pupil is a virtual image inside telescope Its size is A / M obj ts BUT It is located d / M from the eyepiece lens ts TELESCOPES ENHANCE BRIGHTNESS OF POINT SOURCES (STARS) Bailey AAO 2016 4 1/29/16 STARS OR POINT SOURCES Bottom line on brightness Retinal image is smaller than a receptor diameter For Point Sources As the eye gets closer to a point source, the pupil becomes larger in angular size and captures more light from the point. The size of the image of the point is NOT changed. FOR POINT SOURCES Entrance pupil determines brightness Image brightness determined by the area of light capture Inverse square rule for point sources Either TS objective OR M times eye pupil, 2 (whichever is smaller) Image illuminance ∝ 1 / d FOR EXTENDED SOURCES Image brightness determined by size of beam to enter eye For extended sources (large objects) Either eye pupil OR exit pupil of TS, Object does not get brighter (whichever is smaller) Retinal image of object gets larger, but average retinal illuminance remains the same All images from the system are FIELD ASPECT RATIOS within the Image Field Cone IFAR = 10 cm/30 cm Image Field Aspect Ratio (IFAR) Is the ratio of the diameter of FoV = 0.33 = 19° 20 cm at 60 cm Field limiter image space aperture that limits the field 10 cm diameter to its distance from the eye point. Aperture in a card Object Field Aspect Ratio (OFAR) E FoV 5 cm at 15 cm Is the ratio of the diameter of object space aperture that limits the field to its distance from the object space representation of the eye point Eye-to-aperture For Telescopes, IFAR = M (OFAR) = 30 cm Field of View for simple Rule of thumb for Galilean and Keplerian telescopes Fields of View of Telescopes Keplerian Keplerian telescopes (Usually IFAR ≈1) IFAR = A2 / z Keplerian or IFAR = A2 /(d/M) Field limitation by Ocular lens FoV ≈ EVD (or field lens?) Ocular lens subtends a large angle at the eye Galilean Telescopes (Usually IFAR = 1/Mts) Galilean FoV ≈ EVD / Mts Field limitation by image of objective (exit pupil of TS) Depth oF Field oF Telescopes TS exit pupil is small 2 and remote. Thus DoF≈EVD Galilean subtends a small angle at the eye IFAR = (A1 /M) / (z + d/M) 4x12 TS with +5.00D cap EVD = (20 cm / 4) = 5cm = 0.05m DoF ≈ (0.05)2 = 0.0025 m = 2.5 mm Bailey AAO 2016 5 1/29/16 Field of Fixation is smaller than Field of View Imaging through afocal telescopes finite object distances Field of View Extent of peripheral vision during central fixation Field restricting aperture and its distance from the
Load more

Recommended publications
  • Breaking Down the “Cosine Fourth Power Law”
    Breaking Down The “Cosine Fourth Power Law” By Ronian Siew, inopticalsolutions.com Why are the corners of the field of view in the image captured by a camera lens usually darker than the center? For one thing, camera lenses by design often introduce “vignetting” into the image, which is the deliberate clipping of rays at the corners of the field of view in order to cut away excessive lens aberrations. But, it is also known that corner areas in an image can get dark even without vignetting, due in part to the so-called “cosine fourth power law.” 1 According to this “law,” when a lens projects the image of a uniform source onto a screen, in the absence of vignetting, the illumination flux density (i.e., the optical power per unit area) across the screen from the center to the edge varies according to the fourth power of the cosine of the angle between the optic axis and the oblique ray striking the screen. Actually, optical designers know this “law” does not apply generally to all lens conditions.2 – 10 Fundamental principles of optical radiative flux transfer in lens systems allow one to tune the illumination distribution across the image by varying lens design characteristics. In this article, we take a tour into the fascinating physics governing the illumination of images in lens systems. Relative Illumination In Lens Systems In lens design, one characterizes the illumination distribution across the screen where the image resides in terms of a quantity known as the lens’ relative illumination — the ratio of the irradiance (i.e., the power per unit area) at any off-axis position of the image to the irradiance at the center of the image.
    [Show full text]
  • Geometrical Irradiance Changes in a Symmetric Optical System
    Geometrical irradiance changes in a symmetric optical system Dmitry Reshidko Jose Sasian Dmitry Reshidko, Jose Sasian, “Geometrical irradiance changes in a symmetric optical system,” Opt. Eng. 56(1), 015104 (2017), doi: 10.1117/1.OE.56.1.015104. Downloaded From: https://www.spiedigitallibrary.org/journals/Optical-Engineering on 11/28/2017 Terms of Use: https://www.spiedigitallibrary.org/terms-of-use Optical Engineering 56(1), 015104 (January 2017) Geometrical irradiance changes in a symmetric optical system Dmitry Reshidko* and Jose Sasian University of Arizona, College of Optical Sciences, 1630 East University Boulevard, Tucson 85721, United States Abstract. The concept of the aberration function is extended to define two functions that describe the light irra- diance distribution at the exit pupil plane and at the image plane of an axially symmetric optical system. Similar to the wavefront aberration function, the irradiance function is expanded as a polynomial, where individual terms represent basic irradiance distribution patterns. Conservation of flux in optical imaging systems is used to derive the specific relation between the irradiance coefficients and wavefront aberration coefficients. It is shown that the coefficients of the irradiance functions can be expressed in terms of wavefront aberration coefficients and first- order system quantities. The theoretical results—these are irradiance coefficient formulas—are in agreement with real ray tracing. © 2017 Society of Photo-Optical Instrumentation Engineers (SPIE) [DOI: 10.1117/1.OE.56.1.015104] Keywords: aberration theory; wavefront aberrations; irradiance. Paper 161674 received Oct. 26, 2016; accepted for publication Dec. 20, 2016; published online Jan. 23, 2017. 1 Introduction the normalized field H~ and aperture ρ~ vectors.
    [Show full text]
  • Beam Expander Basics: Not All Spots Are Created Equal
    LEARNING – UNDERSTANDING – INTRODUCING – APPLYING Beam Expander Basics: Not All Spots Are Created Equal APPLICATION NOTES www.edmundoptics.com BEAM EXPANDERS A laser beam expander is designed to increase the diameter from well-established optical telescope fundamentals. In such of a collimated input beam to a larger collimated output beam. systems, the object rays, located at infinity, enter parallel to Beam expanders are used in applications such as laser scan- the optical axis of the internal optics and exit parallel to them ning, interferometry, and remote sensing. Contemporary laser as well. This means that there is no focal length to the entire beam expander designs are afocal systems that developed system. THEORY: TELESCOPES Optical telescopes, which have classically been used to view eye, or image created, is called the image lens. distant objects such as celestial bodies in outer space, are di- vided into two types: refracting and reflecting. Refracting tele- A Galilean telescope consists of a positive lens and a negative scopes utilize lenses to refract or bend light while reflecting lens that are also separated by the sum of their focal length telescopes utilize mirrors to reflect light. (Figure 2). However, since one of the lenses is negative, the separation distance between the two lenses is much shorter Refracting telescopes fall into two categories: Keplerian and than in the Keplerian design. Please note that using the Effec- Galilean. A Keplerian telescope consists of positive focal length tive Focal Length of the two lenses will give a good approxima- lenses that are separated by the sum of their focal lengths (Fig- tion of the total length, while using the Back Focal Length will ure 1).
    [Show full text]
  • Nikon Binocular Handbook
    THE COMPLETE BINOCULAR HANDBOOK While Nikon engineers of semiconductor-manufactur- FINDING THE ing equipment employ our optics to create the world’s CONTENTS PERFECT BINOCULAR most precise instrumentation. For Nikon, delivering a peerless vision is second nature, strengthened over 4 BINOCULAR OPTICS 101 ZOOM BINOCULARS the decades through constant application. At Nikon WHAT “WATERPROOF” REALLY MEANS FOR YOUR NEEDS 5 THE RELATIONSHIP BETWEEN POWER, Sport Optics, our mission is not just to meet your THE DESIGN EYE RELIEF, AND FIELD OF VIEW The old adage “the better you understand some- PORRO PRISM BINOCULARS demands, but to exceed your expectations. ROOF PRISM BINOCULARS thing—the more you’ll appreciate it” is especially true 12-14 WHERE QUALITY AND with optics. Nikon’s goal in producing this guide is to 6-11 THE NUMBERS COUNT QUANTITY COUNT not only help you understand optics, but also the EYE RELIEF/EYECUP USAGE LENS COATINGS EXIT PUPIL ABERRATIONS difference a quality optic can make in your appre- REAL FIELD OF VIEW ED GLASS AND SECONDARY SPECTRUMS ciation and intensity of every rare, special and daily APPARENT FIELD OF VIEW viewing experience. FIELD OF VIEW AT 1000 METERS 15-17 HOW TO CHOOSE FIELD FLATTENING (SUPER-WIDE) SELECTING A BINOCULAR BASED Nikon’s WX BINOCULAR UPON INTENDED APPLICATION LIGHT DELIVERY RESOLUTION 18-19 BINOCULAR OPTICS INTERPUPILLARY DISTANCE GLOSSARY DIOPTER ADJUSTMENT FOCUSING MECHANISMS INTERNAL ANTIREFLECTION OPTICS FIRST The guiding principle behind every Nikon since 1917 product has always been to engineer it from the inside out. By creating an optical system specific to the function of each product, Nikon can better match the product attri- butes specifically to the needs of the user.
    [Show full text]
  • Technical Aspects and Clinical Usage of Keplerian and Galilean Binocular Surgical Loupe Telescopes Used in Dentistry Or Medicine
    Surgical and Dental Ergonomic Loupes Magnification and Microscope Design Principles Technical Aspects and Clinical Usage of Keplerian and Galilean Binocular Surgical Loupe Telescopes used in Dentistry or Medicine John Mamoun, DMD1, Mark E. Wilkinson, OD2 , Richard Feinbloom3 1Private Practice, Manalapan, NJ, USA 2Clinical Professor of Opthalmology at the University of Iowa Carver College of Medicine, Department of Ophthalmology and Visual Sciences, Iowa City, IA, USA, and the director, Vision Rehabilitation Service, University of Iowa Carver Family Center for Macular Degeneration 3President, Designs for Vision, Inc., Ronkonkoma, NY Open Access Dental Lecture No.2: This Article is Public Domain. Published online, December 2013 Abstract Dentists often use unaided vision, or low-power telescopic loupes of 2.5-3.0x magnification, when performing dental procedures. However, some clinically relevant microscopic intra-oral details may not be visible with low magnification. About 1% of dentists use a surgical operating microscope that provides 5-20x magnification and co-axial illumination. However, a surgical operating microscope is not as portable as a surgical telescope, which are available in magnifications of 6-8x. This article reviews the technical aspects of the design of Galilean and Keplerian telescopic binocular loupes, also called telemicroscopes, and explains how these technical aspects affect the clinical performance of the loupes when performing dental tasks. Topics include: telescope lens systems, linear magnification, the exit pupil, the depth of field, the field of view, the image inverting Schmidt-Pechan prism that is used in the Keplerian telescope, determining the magnification power of lens systems, and the technical problems with designing Galilean and Keplerian loupes of extremely high magnification, beyond 8.0x.
    [Show full text]
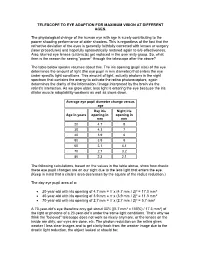
  • TELESCOPE to EYE ADAPTION for MAXIMUM VISION at DIFFERENT AGES. the Physiological Change of the Human Eye with Age Is Surely
    TELESCOPE TO EYE ADAPTION FOR MAXIMUM VISION AT DIFFERENT AGES. The physiological change of the human eye with age is surely contributing to the poorer shooting performance of older shooters. This is regardless of the fact that the refractive deviation of the eyes is generally faithfully corrected with lenses or surgery (laser procedures) and hopefully optometrically restored again to 6/6 effectiveness. Also, blurred eye lenses (cataracts) get replaced in the over sixty group. So, what then is the reason for seeing “poorer” through the telescope after the above? The table below speaks volumes about this. The iris opening (pupil size) of the eye determines the amount of light (the eye pupil in mm diameter) that enters the eye under specific light conditions. This amount of light, actually photons in the sight spectrum that contains the energy to activate the retina photoreceptors, again determines the clarity of the information / image interpreted by the brain via the retina's interaction. As we grow older, less light is entering the eye because the iris dilator muscle adaptability weakens as well as slows down. Average eye pupil diameter change versus age Day iris Night iris Age in years opening in opening in mm mm 20 4.7 8 30 4.3 7 40 3.9 6 50 3.5 5 60 3.1 4.1 70 2.7 3.2 80 2.3 2.5 The following calculations, based on the values in the table above, show how drastic these eye pupil changes are on our sight due to the less light that enters the eye.
    [Show full text]
  • Part 4: Filed and Aperture, Stop, Pupil, Vignetting Herbert Gross
    Optical Engineering Part 4: Filed and aperture, stop, pupil, vignetting Herbert Gross Summer term 2020 www.iap.uni-jena.de 2 Contents . Definition of field and aperture . Numerical aperture and F-number . Stop and pupil . Vignetting Optical system stop . Pupil stop defines: 1. chief ray angle w 2. aperture cone angle u . The chief ray gives the center line of the oblique ray cone of an off-axis object point . The coma rays limit the off-axis ray cone . The marginal rays limit the axial ray cone stop pupil coma ray marginal ray y field angle image w u object aperture angle y' chief ray 4 Definition of Aperture and Field . Imaging on axis: circular / rotational symmetry Only spherical aberration and chromatical aberrations . Finite field size, object point off-axis: - chief ray as reference - skew ray bundels: y y' coma and distortion y p y'p - Vignetting, cone of ray bundle not circular O' field of marginal/rim symmetric view ray RAP' chief ray - to distinguish: u w' u' w tangential and sagittal chief ray plane O entrance object exit image pupil plane pupil plane 5 Numerical Aperture and F-number image . Classical measure for the opening: plane numerical aperture (half cone angle) object in infinity NA' nsinu' DEnP/2 u' . In particular for camera lenses with object at infinity: F-number f f F# DEnP . Numerical aperture and F-number are to system properties, they are related to a conjugate object/image location 1 . Paraxial relation F # 2n'tanu' . Special case for small angles or sine-condition corrected systems 1 F # 2NA' 6 Generalized F-Number .
    [Show full text]
  • The F-Word in Optics
    The F-word in Optics F-number, was first found for fixing photographic exposure. But F/number is a far more flexible phenomenon for finding facts about optics. Douglas Goodman finds fertile field for fixes for frequent confusion for F/#. The F-word of optics is the F-number,* also known as F/number, F/#, etc. The F- number is not a natural physical quantity, it is not defined and used consistently, and it is often used in ways that are both wrong and confusing. Moreover, there is no need to use the F-number, since what it purports to describe can be specified rigorously and unambiguously with direction cosines. The F-number is usually defined as follows: focal length F-number= [1] entrance pupil diameter A further identification is usually made with ray angle. Referring to Figure 1, a ray from an object at infinity that is parallel to the axis in object space intersects the front principal plane at height Y and presumably leaves the rear principal plane at the same height. If f is the rear focal length, then the angle of the ray in image space θ′' is given by y tan θ'= [2] f In this equation, as in the others here, a sign convention for angles heights and magnifications is not rigorously enforced. Combining these equations gives: 1 F−= number [3] 2tanθ ' For an object not at infinity, by analogy, the F-number is often taken to be the half of the inverse of the tangent of the marginal ray angle. However, Eq. 2 is wrong.
    [Show full text]
  • Head Mounted Display Optics II
    Head Mounted Display Optics II Gordon Wetzstein Stanford University EE 267 Virtual Reality Lecture 8 stanford.edu/class/ee267/ Lecture Overview • focus cues & the vergence-accommodation conflict • advanced optics for VR with focus cues: • gaze-contingent varifocal displays • volumetric and multi-plane displays • near-eye light field displays • Maxwellian-type displays • AR displays Magnified Display • big challenge: virtual image appears at fixed focal plane! d • no focus cues d’ f 1 1 1 + = d d ' f Importance of Focus Cues Decreases with Age - Presbyopia 0D (∞cm) 4D (25cm) 8D (12.5cm) 12D (8cm) Nearest focus distance focus Nearest 16D (6cm) 8 16 24 32 40 48 56 64 72 Age (years) Duane, 1912 Cutting & Vishton, 1995 Relative Importance of Depth Cues The Vergence-Accommodation Conflict (VAC) Real World: Vergence & Accommodation Match! Current VR Displays: Vergence & Accommodation Mismatch Accommodation and Retinal Blur Blur Gradient Driven Accommodation Blur Gradient Driven Accommodation Blur Gradient Driven Accommodation Blur Gradient Driven Accommodation Blur Gradient Driven Accommodation Blur Gradient Driven Accommodation Top View Real World: Vergence & Accommodation Match! Top View Screen Stereo Displays Today (including HMDs): Vergence-Accommodation Mismatch! Consequences of Vergence-Accommodation Conflict • Visual discomfort (eye tiredness & eyestrain) after ~20 minutes of stereoscopic depth judgments (Hoffman et al. 2008; Shibata et al. 2011) • Degrades visual performance in terms of reaction times and acuity for stereoscopic vision
    [Show full text]
  • 6-1 Optical Instrumentation-Stop and Window.Pdf
    6.6. OpticalOptical instrumentationinstrumentation Last chapter ¾ Chromatic Aberration ¾ Third-order (Seidel) Optical Aberrations Spherical aberrations, Coma, Astigmatism, Curvature of Field, Distortion This chapter ¾ Aperture stop, Entrance pupil, Exit pupil ¾ Field stop, Entrance window, Exit window Aperture effects on image ¾ Depth of field, Depth of focus ¾ prism and dispersion ¾ Camera ¾ Magnifier and eyepiece Optical instruments ¾ Microscope ¾ Telescope StopsStops inin OpticalOptical SystemsSystems Larger lens improves the brightness of the image Image of S Two lenses of the same formed at focal length (f), but the same diameter (D) differs place by both lenses SS’ Bundle of rays from S, imaged at S’ More light collected is larger for from S by larger larger lens lens StopsStops inin OpticalOptical SystemsSystems • Brightness of the image is determined primarily by the size of the bundle of rays collected by the system (from each object point) • Stops can be used to reduce aberrations StopsStops inin OpticalOptical SystemsSystems How much of the object we see is determined by: Field of View Q Q’ (not seen) Rays from Q do not pass through system We can only see object points closer to the axis of the system Thus, the Field of view is limited by the system ApertureAperture StopStop • A stop is an opening (despite its name) in a series of lenses, mirrors, diaphragms, etc. • The stop itself is the boundary of the lens or diaphragm • Aperture stop: that element of the optical system that limits the cone of light from any particular object point on the axis of the system ApertureAperture StopStop (AS)(AS) E O Diaphragm E Assume that the Diaphragm is the AS of the system Entrance Pupil (E P) Entrance Pupil (EnnP) The entrance pupil is defined to be the image of the aperture stop in all the lenses preceding it (i.e.
    [Show full text]
  • A Simple but Precise Method for Quantitative Measurement of the Quality of the Laser Focus in a Scanning Optical Microscope
    Journal of Microscopy, Vol. 00, Issue 0 2015, pp. 1–8 doi: 10.1111/jmi.12249 Received 3 December 2014; accepted 24 February 2015 A simple but precise method for quantitative measurement of the quality of the laser focus in a scanning optical microscope J. Trag¨ ardh˚ ∗,K.MacRae∗,†,C.Travis†,R.Amor∗, G. Norris∗, S.H. Wilson∗,†, G.-L. Oppo† & G. McConnell∗ ∗Centre for Biophotonics, Strathclyde Institute for Pharmacy and Biomedical Sciences, University of Strathclyde, Glasgow, U.K †Department of Physics, University of Strathclyde, Glasgow, U.K Key words. Beam characterization, knife-edge measurement, microscopy, resolution. Summary distinguish between fine details of a specimen. According to the Abbe equation, modified by Rayleigh, the lateral resolution We report a method for characterizing the focussing laser r is given by beam exiting the objective in a laser scanning microscope. lat This method provides the size of the optical focus, the diver- 0.61λ r = , (1) gence of the beam, the ellipticity and the astigmatism. We use lat N.A. a microscopic-scale knife edge in the form of a simple trans- mission electron microscopy grid attached to a glass micro- while the axial resolution rax is given by scope slide, and a light-collecting optical fibre and photodiode 2nλ underneath the specimen. By scanning the laser spot from a rax = , (2) (N.A.)2 reflective to a transmitting part of the grid, a beam profile in the form of an error function can be obtained and by repeating where λ is the wavelength, n is the refractive index and N.A.
    [Show full text]
  • Parallax Adjustment for Riflescopes
    Parallax Adjustment For Riflescopes As applied to riflescopes, parallax can be defined as the apparent movement of objects within the field of view in relation to the reticle. Parallax occurs when the “primary image” of the object is formed either in front of, or behind the reticle. If the eye is moved from the optical axis of the scope, this also creates parallax. Parallax does not occur if the primary image is formed on the same focal plane as the reticle, or if the eye is positioned in the optical axis of the scope. Riflescopes with high magnification, or scopes for long-range shooting should be equipped with a parallax adjustment because even slight sighting errors can seriously affect sighting accuracy. By adjusting the objective part of the optical system the target can be brought in the exact focal plane of the reticle at any distance. Tactical style riflescopes do not usually have parallax adjustment because the exact range of the target can never be anticipated. Lower magnification scopes do not usually have parallax adjustment either since at lower powers the amount of parallax is very small and has little importance for practical, fast target sighting accuracy. Factors That Affect the Amount of Parallax in a Riflescope Two main factors that cause and affect the amount of parallax in a riflescope. First is the distance of the target to the objective lens of the riflescope. Since the reticle is in a fixed position within the riflescope housing, the image of the target doesn’t always appear positioned in the same plane as the reticle.
    [Show full text]