Characterisation of Young Stellar Clusters⋆
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Observing List Evening of 2011 Dec 25 at Boyden Observatory
Southern Skies Binocular list Observing List Evening of 2011 Dec 25 at Boyden Observatory Sunset 19:20, Twilight ends 20:49, Twilight begins 03:40, Sunrise 05:09, Moon rise 06:47, Moon set 20:00 Completely dark from 20:49 to 03:40. New Moon. All times local (GMT+2). Listing All Classes visible above 2 air mass and in complete darkness after 20:49 and before 03:40. Cls Primary ID Alternate ID Con Mag Size Distance RA 2000 Dec 2000 Begin Optimum End S.A. Ur. 2 PSA Difficulty Optimum EP Open Collinder 227 Melotte 101 Car 8.4 15.0' 6500 ly 10h42m12.0s -65°06'00" 01:32 03:31 03:54 25 210 40 challenging Glob NGC 2808 Car 6.2 14.0' 26000 ly 09h12m03.0s -64°51'48" 21:57 03:08 04:05 25 210 40 detectable Open IC 2602 Collinder 229 Car 1.6 100.0' 520 ly 10h42m58.0s -64°24'00" 23:20 03:31 04:07 25 210 40 obvious Open Collinder 246 Melotte 105 Car 9.4 5.0' 7200 ly 11h19m42.0s -63°29'00" 01:44 03:33 03:57 25 209 40 challenging Open IC 2714 Collinder 245 Car 8.2 14.0' 4000 ly 11h17m27.0s -62°44'00" 01:32 03:33 03:57 25 209 40 challenging Open NGC 2516 Collinder 172 Car 3.3 30.0' 1300 ly 07h58m04.0s -60°45'12" 20:38 01:56 04:10 24 200 30 obvious Open NGC 3114 Collinder 215 Car 4.5 35.0' 3000 ly 10h02m36.0s -60°07'12" 22:43 03:27 04:07 25 199 40 easy Neb NGC 3372 Eta Carinae Nebula Car 3.0 120.0' 10h45m06.0s -59°52'00" 23:26 03:32 04:07 25 199 38 easy Open NGC 3532 Collinder 238 Car 3.4 50.0' 1600 ly 11h05m39.0s -58°45'12" 23:47 03:33 04:08 25 198 38 easy Open NGC 3293 Collinder 224 Car 6.2 6.0' 7600 ly 10h35m51.0s -58°13'48" 23:18 03:32 04:08 25 199 -

The List of Possible Double and Multiple Open Clusters Between Galactic Longitudes 240O and 270O
The list of possible double and multiple open clusters between galactic longitudes 240o and 270o Juan Casado Facultad de Ciencias, Universidad Autónoma de Barcelona, 08193, Bellaterra, Catalonia, Spain Email: [email protected] Abstract This work studies the candidate double and multiple open clusters (OCs) in the galactic sector from l = 240o to l = 270o, which contains the Vela-Puppis star formation region. To do that, we have searched the most recent and complete catalogues of OCs by hand to get an extensive list of 22 groups of OCs involving 80 candidate members. Gaia EDR3 has been used to review some of the candidate OCs and look for new OCs near the candidate groups. Gaia data also permitted filtering out most of the field sources that are not member stars of the OCs. The plotting of combined colour-magnitude diagrams of candidate pairs has allowed, in several cases, endorsing or discarding their link. The most likely systems are formed by OCs less than 0.1 Gyr old, with only one eccentric OC in this respect. No probable system of older OCs has been found. Preliminary estimations of the fraction of known OCs that form part of groups (9.4 to 15%) support the hypothesis that the Galaxy and the Large Magellanic Cloud are similar in this respect. The results indicate that OCs are born in groups like stars are born in OCs. Keywords Binary open clusters; Open cluster groups; Open cluster formation; Gaia; Manual search; Large Magellanic Cloud. 1. Introduction Open clusters are formed in giant molecular clouds and there is observational evidence suggesting that they can form in groups (Camargo et al. -

407 a Abell Galaxy Cluster S 373 (AGC S 373) , 351–353 Achromat
Index A Barnard 72 , 210–211 Abell Galaxy Cluster S 373 (AGC S 373) , Barnard, E.E. , 5, 389 351–353 Barnard’s loop , 5–8 Achromat , 365 Barred-ring spiral galaxy , 235 Adaptive optics (AO) , 377, 378 Barred spiral galaxy , 146, 263, 295, 345, 354 AGC S 373. See Abell Galaxy Cluster Bean Nebulae , 303–305 S 373 (AGC S 373) Bernes 145 , 132, 138, 139 Alnitak , 11 Bernes 157 , 224–226 Alpha Centauri , 129, 151 Beta Centauri , 134, 156 Angular diameter , 364 Beta Chamaeleontis , 269, 275 Antares , 129, 169, 195, 230 Beta Crucis , 137 Anteater Nebula , 184, 222–226 Beta Orionis , 18 Antennae galaxies , 114–115 Bias frames , 393, 398 Antlia , 104, 108, 116 Binning , 391, 392, 398, 404 Apochromat , 365 Black Arrow Cluster , 73, 93, 94 Apus , 240, 248 Blue Straggler Cluster , 169, 170 Aquarius , 339, 342 Bok, B. , 151 Ara , 163, 169, 181, 230 Bok Globules , 98, 216, 269 Arcminutes (arcmins) , 288, 383, 384 Box Nebula , 132, 147, 149 Arcseconds (arcsecs) , 364, 370, 371, 397 Bug Nebula , 184, 190, 192 Arditti, D. , 382 Butterfl y Cluster , 184, 204–205 Arp 245 , 105–106 Bypass (VSNR) , 34, 38, 42–44 AstroArt , 396, 406 Autoguider , 370, 371, 376, 377, 388, 389, 396 Autoguiding , 370, 376–378, 380, 388, 389 C Caldwell Catalogue , 241 Calibration frames , 392–394, 396, B 398–399 B 257 , 198 Camera cool down , 386–387 Barnard 33 , 11–14 Campbell, C.T. , 151 Barnard 47 , 195–197 Canes Venatici , 357 Barnard 51 , 195–197 Canis Major , 4, 17, 21 S. Chadwick and I. Cooper, Imaging the Southern Sky: An Amateur Astronomer’s Guide, 407 Patrick Moore’s Practical -

Ngc Catalogue Ngc Catalogue
NGC CATALOGUE NGC CATALOGUE 1 NGC CATALOGUE Object # Common Name Type Constellation Magnitude RA Dec NGC 1 - Galaxy Pegasus 12.9 00:07:16 27:42:32 NGC 2 - Galaxy Pegasus 14.2 00:07:17 27:40:43 NGC 3 - Galaxy Pisces 13.3 00:07:17 08:18:05 NGC 4 - Galaxy Pisces 15.8 00:07:24 08:22:26 NGC 5 - Galaxy Andromeda 13.3 00:07:49 35:21:46 NGC 6 NGC 20 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 7 - Galaxy Sculptor 13.9 00:08:21 -29:54:59 NGC 8 - Double Star Pegasus - 00:08:45 23:50:19 NGC 9 - Galaxy Pegasus 13.5 00:08:54 23:49:04 NGC 10 - Galaxy Sculptor 12.5 00:08:34 -33:51:28 NGC 11 - Galaxy Andromeda 13.7 00:08:42 37:26:53 NGC 12 - Galaxy Pisces 13.1 00:08:45 04:36:44 NGC 13 - Galaxy Andromeda 13.2 00:08:48 33:25:59 NGC 14 - Galaxy Pegasus 12.1 00:08:46 15:48:57 NGC 15 - Galaxy Pegasus 13.8 00:09:02 21:37:30 NGC 16 - Galaxy Pegasus 12.0 00:09:04 27:43:48 NGC 17 NGC 34 Galaxy Cetus 14.4 00:11:07 -12:06:28 NGC 18 - Double Star Pegasus - 00:09:23 27:43:56 NGC 19 - Galaxy Andromeda 13.3 00:10:41 32:58:58 NGC 20 See NGC 6 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 21 NGC 29 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 22 - Galaxy Pegasus 13.6 00:09:48 27:49:58 NGC 23 - Galaxy Pegasus 12.0 00:09:53 25:55:26 NGC 24 - Galaxy Sculptor 11.6 00:09:56 -24:57:52 NGC 25 - Galaxy Phoenix 13.0 00:09:59 -57:01:13 NGC 26 - Galaxy Pegasus 12.9 00:10:26 25:49:56 NGC 27 - Galaxy Andromeda 13.5 00:10:33 28:59:49 NGC 28 - Galaxy Phoenix 13.8 00:10:25 -56:59:20 NGC 29 See NGC 21 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 30 - Double Star Pegasus - 00:10:51 21:58:39 -

Southern Sky Binocular Observing List
Southern Sky Binocular Observing List Object R.A. DEC Mag PA* Type Size Const Urn SA [ ] NGC 104 00 24.1 -72 05 4.5 ----- GbCl 25.0' Tuc 440 24 [ ] SMC 00 52.8 -72 50 2.7 10 Glxy 316'X186' Tuc 441 24 [ ] NGC 362 01 03.2 -70 51 6.6 ----- GbCl 12.9' Tuc 441 24 [ ] NGC 1261 03 12.3 -55 13 8.4 ----- GbCl 6.9' Hor 419 24 [ ] NGC 1851 05 14.1 -40 03 7.2 ----- GbCl 11.0' Col 393 19 [ ] LMC 05 23.6 -69 45 0.9 170 Glxy 646'X550' Dor 444 24 [ ] NGC 2070 05 38.6 -69 05 8.2 ----- BNeb 40'X25' Dor 445 24 [ ] NGC 2451 07 45.4 -37 58 2.8 ----- OpCl 45.0' Pup 362 19 [ ] NGC 2477 07 52.3 -38 33 5.8 ----- OpCl 27.0' Pup 362 19 [ ] NGC 2516 07 58.3 -60 52 3.8 ----- OpCl 29.0' Car 424 24 [ ] NGC 2547 08 10.7 -49 16 4.7 ----- OpCl 20.0' Vel 396 20 [ ] NGC 2546 08 12.4 -37 38 6.3 ----- OpCl 40.0' Pup 362 20 [ ] NGC 2627 08 37.3 -29 57 8.4 ----- OpCl 11.0' Pyx 363 20 [ ] IC 2391 08 40.2 -53 04 2.5 ----- OpCl 50.0' Vel 425 25 [ ] IC 2395 08 41.1 -48 12 4.6 ----- OpCl 7.0' Vel 397 20 [ ] NGC 2659 08 42.6 -44 57 8.6 ----- OpCl 2.7' Vel 397 20 [ ] NGC 2670 08 45.5 -48 47 7.8 ----- OpCl 9.0' Vel 397 20 [ ] NGC 2808 09 12.0 -64 52 6.3 ----- GbCl 13.8' Car 448 25 [ ] IC 2488 09 27.6 -56 59 7.4 ----- OpCl 14.0' Vel 425 25 [ ] NGC 2910 09 30.4 -52 54 7.2 ----- OpCl 5.0' Vel 426 25 [ ] NGC 2925 09 33.7 -53 26 8.3 ----- OpCl 12.0' Vel 426 25 [ ] NGC 3114 10 02.7 -60 07 4.2 ----- OpCl 35.0' Car 426 25 [ ] NGC 3201 10 17.6 -46 25 6.7 ----- GbCl 18.0' Vel 399 20 [ ] NGC 3228 10 21.8 -51 43 6.0 ----- OpCl 18.0' Vel 426 25 [ ] NGC 3293 10 35.8 -58 14 4.7 ----- OpCl 5.0' Car -

South Binoculars
South Binoculars (66 objects) Object Type Mag Size Information 47 Tucanae GC 4.0 50.0' R00:24:05.2 D-72:04:49 Tucana NGC 104 Type: III NGC 362 GC 6.8 14.0' R01:03:14.3 D-70:50:52 Tucana Type: III NGC 1261 GC 8.3 6.8' R03:12:15.3 D-55:12:59 Horologium Type: II NGC 1851 GC 7.1 12.0' R05:14:06.3 D-40:02:48 Columba Type: II Tarantula Nebula BN 30.0'x20.0' R05:38:42.5 D-69:06:03 Dorado NGC 2070 Type: EN, mag_b: 5.0 NGC 2451 OC 2.8 50.0' R07:45:15.0 D-37:58:00 Puppis Type: II2p NGC 2477 OC 5.8 20.0' R07:52:10.0 D-38:31:48 Puppis Type: I3r NGC 2516 OC 3.8 22.0' R07:58:04.0 D-60:45:12 Carina Type: I3r, mag_b: 3.8 NGC 2547 OC 4.7 25.0' R08:10:09.0 D-49:12:54 Vela Type: II2p NGC 2546 OC 6.3 70.0' R08:12:15.0 D-37:35:42 Puppis Type: III2m NGC 2627 OC 8.4 9.0' R08:37:15.0 D-29:57:18 Pyxis Type: III2m Omicron Velorum OC 2.6 60.0' R08:40:18.0 D-52:55:00 Vela cluster Type: II3p IC 2391 IC 2395 OC 4.6 13.0' R08:42:30.0 D-48:08:12 Vela Type: II3p NGC 2659 OC 8.6 15.0' R08:42:36.0 D-44:59:00 Vela Type: III3m NGC 2670 OC 7.8 7.0' R08:45:30.0 D-48:48:00 Vela Type: II2p NGC 2808 GC 6.2 14.0' R09:12:02.6 D-64:51:45 Carina Type: I IC 2488 OC 7.4 18.0' R09:27:31.0 D-56:58:54 Vela Type: II2m NGC 2910 OC 7.2 6.0' R09:30:29.0 D-52:54:50 Vela Type: I2p NGC 3114 OC 4.2 35.0' R10:02:36.0 D-60:07:00 Carina Type: II3r 1/4 South Binoculars (66 objects) Object Type Mag Size Information NGC 3201 GC 6.9 20.0' R10:17:36.8 D-46:24:38 Vela Type: X NGC 3228 OC 6.0 5.0' R10:21:22.0 D-51:43:42 Vela Type: I1p Gem Cluster OC 4.7 5.0' R10:35:51.0 D-58:13:48 Carina NGC 3293 Type: -

Capa Resumos Final.Indd 1 29/07/2010 15:43:44
Capa_Resumos_Final.indd 1 29/07/2010 15:43:44 ÍNDICE Programa da XXXV Reunião Anual...........................................................................................................i Horários das apresentações dos painéis ................................................................................................vii Lista de Participantes ..............................................................................................................................ix Resumos Conferências..........................................................................................................................................1 Comunicações Orais .............................................................................................................................5 Painéis Astrometria.........................................................................................................................................43 Cosmologia ......................................................................................................................................... 47 Ensino e História ............................................................................................................................... 57 Estrelas ...............................................................................................................................................77 Extragaláctica...................................................................................................................................103 Física Solar -
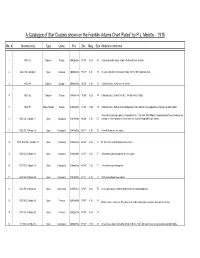
A Catalogue of Star Clusters Shown on the Franklin-Adams Chart Plates” by P.J
A Catalogue of Star Clusters shown on the Franklin-Adams Chart Plates” by P.J. Melotte – 1915 Mel. # Alternative(s) Type Const. R.A. Dec. Mag. Size Melotte's comments 1 NGC 104 Globular Tucana 00h24m04s -72°05' 4.00 50' A typical globular cluster. Bright. Well condensed at centre. 2 NGC 188, Collinder 6 Open Cepheus 00h47m28s +85°15' 9.30 17' "A somewhat ill-defined cluster mostly 14th to 16th magnitude stars. 3 NGC 288 Globular Sculptor 00h52m45s -26°35' 8.10 13' Globular cluster, rather loose at centre. 4 NGC 362 Globular Tucana 01h03m14s -70°50' 6.80 14' Globular cluster. Similar to N.G.C. 104 but smaller. Bright. 5 NGC 371 Diffuse Nebula Tucana 01h03m30s -72°03' 13.80 7.5' Globular cluster. Falls in smaller Magellanic cloud, and has every appearance of being a globular cluster. A few stars clustering together. Resembles N.G.C. 582, 645, 659. Difficult to decide whether these should not be 6 NGC 436, Collinder 11 Open Cassiopeia 01h15m58s +58°48' 9.30 5.0' classed II. All the clusters here resemble one another though differing in extent. 7 NGC 457, Collinder 12 Open Cassiopeia 01h19m35s +58°17' 5.10 20' A small cluster in a rich region. 8 M103, NGC 581, Collinder 14 Open Cassiopeia 01h33m23s +60°39' 6.90 5' M. 103. A few stars forming a loose cluster. 9 NGC 654, Collinder 18 Open Cassiopeia 01h44m00s +61°53' 8.20 5' A few stars clustered together in a rich region. 10 NGC 659, Collinder 19 Open Cassiopeia 01h44m24s +60°40' 7.20 5' A few stars clustered together. -
The Evolutionary Status of Be Stars: Results from a Photometric Study Of
The Evolutionary Status of Be Stars: Results from a Photometric Study of Southern Open Clusters M. Virginia McSwain1,2 Department of Astronomy, Yale University, P.O. Box 208101, New Haven, CT 06520-8101 [email protected] Douglas R. Gies Department of Physics and Astronomy, Georgia State University, P.O. Box 4106, Atlanta, GA 30302-4106 [email protected] ABSTRACT Be stars are a class of rapidly rotating B stars with circumstellar disks that cause Balmer and other line emission. There are three possible reasons for the rapid rotation of Be stars: they may have been born as rapid rotators, spun up by binary mass transfer, or spun up during the main- sequence (MS) evolution of B stars. To test the various formation scenarios, we have conducted a photometric survey of 55 open clusters in the southern sky. Of these, five clusters are probably not physically associated groups and our results for two other clusters are not reliable, but we identify 52 definite Be stars and an additional 129 Be candidates in the remaining clusters. We use our results to examine the age and evolutionary dependence of the Be phenomenon. We find an overall increase in the fraction of Be stars with age until 100 Myr, and Be stars are most common among the brightest, most massive B-type stars above the zero-age MS (ZAMS). We show that a spin-up phase at the terminal-age MS (TAMS) cannot produce the observed distribution of Be stars, but up to 73% of the Be stars detected may have been spun-up by binary mass transfer. -

Constellations T
1 Name Type Mag. Size Con. NGC 1502 Open cluster 6.9 8.0' Cam Áquila Aql Líbra Lib IC 342 Galaxy 9.1 20.9'x20.4' Cam NGC 1513 Open cluster 8.4 9.0' Per Ára Ara Lúpus Lup Áries Ari Lynx Lyn IC 1396 Open cluster 3.5 89.0' Cep NGC 1528 Open cluster 6.4 24.0' Per Auríga Aur Lýra Lyr IC 1805 Open cluster 6.5 60.0'x60.0' Cas NGC 1545 Open cluster 6.2 18.0' Per Boótes Boo Ménsa Men IC 1848 Open cluster 6.5 40.0'x10.0' Cas NGC 1605 Open cluster 10.7 5.0' Per Cáélum Cae Microscópium Mic IC 2574 Galaxy 10.8 12.9'x5.3' UMa NGC 2126 Open cluster 10.2 6.0' Aur Camelopárdalis Cam Monóceros Mon Cáncer Cnc Músca Mus M 52 Open cluster 6.9 13.0' Cas NGC 2403C7 Galaxy 8.9 23.4'x11.8' Cam Cánes Venátici CVn Nórma Nor M 81* Galaxy 7.8 24.9'x11.5' UMa NGC 2768 Galaxy 10.9 8.2'x5.3' UMa Cánis Májor CMa Óctans Oct M 82* Galaxy 9.2 10.5'x5.1' UMa NGC 2976 Galaxy 10.8 6.2'x3.1' UMa Cánis Mínor CMi Ophiúchus Oph M 102 Galaxy 10.8 6.5'x3.1' Dra NGC 3077 Galaxy 10.6 5.2'x4.7' UMa Capricórnus Cap Oríon Ori Carína Car Pávo Pav M 103 Open cluster 7.4 6.0' Cas NGC 4125 Galaxy 10.6 6.0'x5.1' Dra Cassiopéia Cas Pégasus Peg C2 NGC 40 Planetary nebula 10.7 37.0" Cep NGC 4236C3 Galaxy 10.7 22.6'x6.9' Dra Centáurus Cen Pérseus Per NGC 103 Open cluster 9.8 5.0' Cas NGC 4605 Galaxy 10.8 5.9'x2.4' UMa Cephéus Cep Phóénix Phe C1 NGC 188 Open cluster 8.1 15' Cep NGC 6229 Globular cluster 9.4 3.8' Her Cétus Cet Píctor Pic Chamáéleon Cha Písces Psc NGC 129 Open cluster 6.5 21.0' Cas NGC 6503 Galaxy 10.9 7.0'x2.5' Dra Círcinus Cir Píscis Austrínus PsA NGC 133 Open cluster 9.4 7.0' -

The Use of Artificial Intelligence in the Search for Structural Parameters Of
v.1, n.1, p.2-18, 2018. The use of artificial intelligence in the search for structural parameters of clusters of young stars A. Hetem1, S. E. Matsuda Sampa1, J. L. Lima Berretta1 1Federal University of ABC ABSTRACT Due to the huge amount of data available to the astrophysicists nowadays it is imperative to use state of the art tools in the many processes involving data reduction, data traformation and generation of high level indicators in order to advance to the physical analysis. With the rise of huge parallel computer resources, it is possible to concatenate the many Artificial Inteligence tools necessary to model the astrophysical data. We present a realization of this idea applied to a real case of astrophysical study: the analysis of a large sample of clusters of young stars in order to investigate the inherent properties of clustering and dynamic evolution of stellar components. To achieve the statistical parameter Q measured for each cluster, it is necessary to pass the original star data set through a series of processes, each one with its own characteriscits, needs and behaviour. So, we present a set of results obtained by the proposed method and some perspectives of future work in this path. Keywords: artificial inteligence; genetic algorithm; cross-entropy; physical-mathematical model; young star cluster. INTRODUCTION Clusters of young stars In our galaxy it is possible to find some groups of stars that move as an unity, when compared to the other stars. In the studies of stellar evolution, the open clusters are very important objects because their members (stars) are of similar chemical composition and same age. -

A Abell 21, 20–21 Abell 37, 164 Abell 50, 264 Abell 262, 380 Abell 426, 402 Abell 779, 51 Abell 1367, 94 Abell 1656, 147–148
Index A 308, 321, 360, 379, 383, Aquarius Dwarf, 295 Abell 21, 20–21 397, 424, 445 Aquila, 257, 259, 262–264, 266–268, Abell 37, 164 Almach, 382–383, 391 270, 272, 273–274, 279, Abell 50, 264 Alnitak, 447–449 295 Abell 262, 380 Alpha Centauri C, 169 57 Aquila, 279 Abell 426, 402 Alpha Persei Association, Ara, 202, 204, 206, 209, 212, Abell 779, 51 404–405 220–222, 225, 267 Abell 1367, 94 Al Rischa, 381–382, 385 Ariadne’s Hair, 114 Abell 1656, 147–148 Al Sufi, Abdal-Rahman, 356 Arich, 136 Abell 2065, 181 Al Sufi’s Cluster, 271 Aries, 372, 379–381, 383, 392, 398, Abell 2151, 188–189 Al Suhail, 35 406 Abell 3526, 141 Alya, 249, 255, 262 Aristotle, 6 Abell 3716, 297 Andromeda, 327, 337, 339, 345, Arrakis, 212 Achird, 360 354–357, 360, 366, 372, Auriga, 4, 291, 425, 429–430, Acrux, 113, 118, 138 376, 380, 382–383, 388, 434–436, 438–439, 441, Adhara, 7 391 451–452, 454 ADS 5951, 14 Andromeda Galaxy, 8, 109, 140, 157, Avery’s Island, 13 ADS 8573, 120 325, 340, 345, 351, AE Aurigae, 435 354–357, 388 B Aitken, Robert, 14 Antalova 2, 224 Baby Eskimo Nebula, 124 Albino Butterfly Nebula, 29–30 Antares, 187, 192, 194–197 Baby Nebula, 399 Albireo, 70, 269, 271–272, 379 Antennae, 99–100 Barbell Nebula, 376 Alcor, 153 Antlia, 55, 59, 63, 70, 82 Barnard 7, 425 Alfirk, 304, 307–308 Apes, 398 Barnard 29, 430 Algedi, 286 Apple Core Nebula, 280 Barnard 33, 450 Algieba, 64, 67 Apus, 173, 192, 214 Barnard 72, 219 Algol, 395, 399, 402 94 Aquarii, 335 Barnard 86, 233, 241 Algorab, 98, 114, 120, 136 Aquarius, 295, 297–298, 302, 310, Barnard 92, 246 Allen, Richard Hinckley, 5, 120, 136, 320, 324–325, 333–335, Barnard 114, 260 146, 188, 258, 272, 286, 340–341 Barnard 118, 260 M.E.