DOCSLIB.ORG

Some Thermodynamic and Quantum Aspects of NMR Signal Detection Stanislav Sýkora URL of This Document: DOI: 10.3247/Sl4nmr11.002

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Some Thermodynamic and Quantum Aspects of NMR Signal Detection Stanislav Sýkora URL of This Document: DOI: 10.3247/Sl4nmr11.002 Some Thermodynamic and Quantum Aspects of NMR Signal Detection Stanislav Sýkora URL of this document: www.ebyte.it/stan/Talk_BFF6_2011.html DOI: 10.3247/SL4nmr11.002 Presented at 6th BFF on Magnetic Resonance Microsystem , Saig/Titisee (Freiburg), Germany, 26-29 July 2011 Controversies about the nature of NMR signal and its most common modes of detection There is a growing body of literature showing that the foundations of Magnetic Resonance are not as well understood as they should be Principle articles: Bloch F., Nuclear Induction , Phys.Rev. 70, 460-474 (1946). Dicke R.H., Coherence in Spontaneous Radiation Processes , Phys.Rev. 93, 99-110 (1954). Hoult D.I., Bhakar B., NMR signal reception: Virtual photons and coherent spontaneous emission , Concepts Magn. Reson. 9, 277-297 (1997). Hoult D.I., Ginsberg N.S., The quantum origins of the free induction decay and spin noise , J.Magn.Reson. 148, 182-199 (2001). Jeener J., Henin F., A presentation of pulsed nuclear magnetic resonance with full quantization of the radio frequency magnetic field , J.Chem.Phys. 116, 8036-8047 (2002). Hoult D.I., The origins and present status of the radio wave controversy in NMR , Concepts in Magn.Reson. 34A, 193-216 (2009). Stan Sykora 6th BFF 2011, Freiburg, Germany Controversies about the nature of NMR signal and its most common modes of detection This author’s presentations: Magnetic Resonance in Astronomy: Feasibility Considerations , XXXVI GIDRM, 2006. Perpectives of Passive and Active Magnetic Resonance in Astronomy, 22nd NMR Valtice 2007. Spin Radiation, remote MR Spectroscopy, and MR Astronomy , 50th ENC, 2009. Signal Detection: Virtual photons and coherent spontaneous emission , 18th ISMRM, 2010. The Many Walks of Magnetic Resonance: Past, Present and Beyond, Uni Cantabria, Santander, 2010. Do we really understand Magnetic Resonance? , MMCE, 2011. Slides and more info: see www.ebyte.it/stan/SS_Lectures.html Stan Sykora 6th BFF 2011, Freiburg, Germany Questions, questions, questions … for which there should exist simple answers, but … do they? (we have no time for these points now, but I have a handout and we can discuss them during the meeting) 1) Why do we use different explanations for different aspects of MR ? 2) Which aspects of MR are undeniably quantum and cannot be described classically ? 3) Are Bloch equations classical? Is it sensible to try derive them from quantum theory ? 4) Is electromagnetic radiation involved in magnetic resonance? If so, is it true or virtual ? 5) Does spontaneous emission from spin systems occur? If so, what are its properties ? 6) Is MR a near or a far phenomenon? Is remote excitation and/or detection possible ? 7) Can an FID be described as coherent spontaneous emission ? What about CW-NMR ? 8) How do the spins interact with nearby conductors, and with the coil ? 9) Which phenomena can be described considering an isolated spin, and which can’t ? a) What is the role of relaxation processes in all this? Are they essential or marginal ? b) What is the role of time-averaged Hamiltonians in magnetic resonance ? c) Can an FID be described as a sum of individual quantum transitions ? d) Does all this uncover some gaping holes in quantum physics ? e) Does all this tell us something about the ontology of photons ? f) Can MR throw new light on basic aspects of physics ? Stan Sykora 6th BFF 2011, Freiburg, Germany We use different descriptions for different MR phenomena ! Q < 10 4 11 B 3/2 Q = ω/∆ω ≈ 10 1 M 1/2 ⊥⊥⊥ Z' ≡≡≡Z 1/2 ωn 0 -1/2 M|| M(0) -1/2 -1 M α M(t) -3/2 Y' B1 X' CLASSICAL HYBRID QUANTUM Induction law, Thermal equilibrium Coupled spins spectroscopy, Bloch equations, Theory of CW-MR Spin systems dynamics, Reciprocity theorem, Quantum coherences Hilbert/Liouville QM, Simplified MRI, Operator products Density matrix,… Stan Sykora MMCE 2011, Tatranska Lomnica, Slovakia The principle difficulty: How to reconcile the manifestly quantum aspects of MR phenomena with the totally classical nature of the detection/excitation devices Possible ways to tackle the problem A. Rely on paradigms shared by both classical and quantum physics Thermodynamics, Conservation Laws and (some) Statistical Physics A problem: the approach provides good insights but remains incomplete B. Approximate quantum spin systems in a classical way A problem: arisal of a transversal magnetization from parallel spin eigenstates C. Provide a quantum description of the detection/excitation devices A problem: apparent complexity and necessity to conform to classical results An extra task: how to couple the spin system to the detection/excitation device Stan Sykora 6th BFF 2011, Freiburg, Germany The two parts of this talk: A. Part I: Classical paradigms shared also by quantum physics Thermodynamics, Conservation Laws and (some) Statistical Physics B. Approximate quantum spin systems in a classical way A problem: everybody does this since 50 years, therefore I don’t dig it C. Part II: Quantum description of the detection/excitation devices An extra task: coupling the spin system to the detection/excitation device Stan Sykora 6th BFF 2011, Freiburg, Germany Let us forget quantum physics for a while ☺☺☺ and remember just the conservation of energy (the first law of thermodynamics) The physical system we will consider: L Loop and its Inductance R Resistance (may be distributed) J Electric current P just a Point B Magnetic Field m Magnetic Dipole B H = µ = µβ Jτττβ , where µ is the permaebility, β a constant, and τττβ a unit vector. β and τττβ depend only on the system’s geometry. m m = m τττm , where τττm is a unit vector along Stan Sykora 6th BFF 2011, Freiburg, Germany Setting up a master equation Energy terms: 2 Inductive: EL = LJ /2 2 Self-energy of m: Em = km /2 m B Interaction: Ei = - . = -κmJ , where κ = µβ (τττβ.τττm) Dissipation: dE/dt = -J2R Since R is the only dissipative element in the circuit, the energy conservation law dictates 2 dE/dt = dE L/dt + dE i/dt + dE m/dt = -J R Hence, using the apostrophe to denote time derivatives, (LJ -γm)J' - κm'J + RJ 2 +kmm' = 0 Stan Sykora 6th BFF 2011, Freiburg, Germany … a couple of useful notes … Energy terms: 2 Inductive: EL = LJ /2 2 Self-energy of m: Em = km /2 m B Interaction: Ei = - . = -γmJ , where κ = µβ (τττβ.τττm) Dissipation: dE/dt = -J2R 2 2 2 2 † Since EL = LJ /2 and also EL = ∫∫∫V|B| dτ/2 µ = µJ ∫∫∫V β dτ/2 , 2 2 we have L = µ∫∫∫V β dτ = µ<β > V showing that, upon scaling, β correlates with L1/2 The old terms coil volume and filling factor arise from here † While β is positive by definition, κ = µβ (τττβ.τττm) can be both positive or negative Stan Sykora 6th BFF 2011, Freiburg, Germany (A,B) Special cases of the master equation (LJ -γm)J' - κm'J + RJ 2 +kmm' = 0 A. When there is no magnetic dipole (m = m' = 0 ), we get 2 - (R/L) t LJJ' + RJ = 0 ⇒ LJ' + RJ = 0 ⇒ J = J 0 e This is the well-known equation of the LR-circuit . B. The term kmm' is the power needed to maintain the dipole. This is null in the case of quantum particles . It drops out also when the dipole is associated with a permanent magnet or when it is driven driven by an external device. In such cases k=0 and we have a modified master equation: LJJ' - κmJ' - κm'J + J 2R = 0 Stan Sykora 6th BFF 2011, Freiburg, Germany (C) Special cases of the modified master equation LJJ' - κmJ' - κm'J + J 2R = 0 How must the dipole evolve to maintain a constant current ? J’ = 0 The answer is that m must grow linearly with time at the rate m' = JR/ κ One can reverse the point of view and say that this is as though the linearly increasing dipole generated in the circuit the emf Vemf = JR = κm' = µβ (τττβ.τττm) m' which coincides exactly with the classical law of induction . It is easy to show that this holds also when J’≠ 0, provided the induction law is properly extended ( LJ = κm = - Φ). Stan Sykora 6th BFF 2011, Freiburg, Germany (D-E) Oscillating magnetic dipoles LJJ' - κmJ' - κm'J + J 2R = 0 D. What if the dipole is made to oscillate? Let m = m 0 exp(i ωt) and assume a solution of the type J = J 0 exp[i( ωt+ ϕ)]. Then the master equation gives J0 = 2 κω m0/|R+i ωL| and tan( ϕ) = R/ ωL. E. The amplitude of the detected current (signal) is proportional to κ and therefore also to β. Since β describes the efficiency B/J of a current J to generate the field B at point P, this proves the reciprocity theorem : The larger is the field B generated at a point P by a current J in the loop, the stronger is the detected signal due to an oscillating dipole located at P. Hoult D.I., The principle of reciprocity in signal strength calculations - a mathematical guide , Concepts in Magn. Reson. <b>12</b>, 173-187 (2000). Stan Sykora 6th BFF 2011, Freiburg, Germany (F) Current detection of oscillating dipoles J0 = 2 κω m0/|R+i ωL| Detected signal current J0,max = 2 κm0/L is attained for R=0 ½ NJ = [4kTB w/R] Johnson noise current -½ ½ (S/N) J = J 0/N J = ωκ m0 (kTB w) R / |R+i ωL| ½ -½ -½ (S/N) J,max = m 0 ω (2kTB w) κL is attained at R= ωL Comment: While the maximum current is obtained for infinite-Q loops (R=0 ), the best S/N ratio is attained for the “matching” condition R = ωL Stan Sykora 6th BFF 2011, Freiburg, Germany (G) Voltage detection of oscillating dipoles V0 = J 0R = 2 ωκ m0 R/|R+i ωL| Detected signal voltage V0,max = 2 ωκ m0 is attained for R= ∞ ½ NV = [4kTB wR] Johnson noise voltage -½ ½ (S/N) V = V 0 /N V = ωκ m0 (kTB w) R / |R+i ωL| ½ -½ -½ (S/N) V,max = m 0 ω (2kTB w) κL is again attained at R= ωL Comment: While the maximum voltage is obtained for open loops (R = ∞), the best S/N ratio is attained for the “matching” condition R = ωL.
Load more

Recommended publications
  • Few-Electron Ultrastrong Light-Matter Coupling in a Quantum LC Circuit
    PHYSICAL REVIEW X 4, 041031 (2014) Few-Electron Ultrastrong Light-Matter Coupling in a Quantum LC Circuit Yanko Todorov and Carlo Sirtori Université Paris Diderot, Sorbonne Paris Cité, Laboratoire Matériaux et Phénomènes Quantiques, CNRS-UMR 7162, 75013 Paris, France (Received 19 March 2014; revised manuscript received 23 October 2014; published 18 November 2014) The phenomenon of ultrastrong light-matter interaction of a two-dimensional electron gas within a lumped element electronic circuit resonator is explored. The gas is coupled through the oscillating electric field of the capacitor, and in the limit of very small capacitor volumes, the total number of electrons of the system can be reduced to only a few. One of the peculiar features of our quantum mechanical system is that its Hamiltonian evolves from the fermionic Rabi model to the bosonic Hopfield model for light-matter coupling as the number of electrons is increased. We show that the Dicke states, introduced to describe the atomic super-radiance, are the natural base to describe the crossover between the two models. Furthermore, we illustrate how the ultrastrong coupling regime in the system and the associated antiresonant terms of the quantum Hamiltonian have a fundamentally different impact in the fermionic and bosonic cases. In the intermediate regime, our system behaves like a multilevel quantum bit with nonharmonic energy spacing, owing to the particle-particle interactions. Such a system can be inserted into a technological semi- conductor platform, thus opening interesting perspectives for electronic devices where the readout of quantum electrodynamical properties is obtained via the measure of a DC current.
    [Show full text]
  • Anna University Chennai :: Chennai 600 025
    ITEM NO. FI 13.07(3) ANNA UNIVERSITY CHENNAI :: CHENNAI 600 025 UNIVERSITY DEPARTMENTS CURRICULUM – R 2009 B.E. (PART TIME) ELECTRONICS AND COMMUNICATION ENGINEERING SEMESTER I COURSE S.NO. COURSE TITLE L T P C CODE THEORY 1. PTMA9111 Applied Mathematics 3 1 0 4 2. PTPH 9111 Applied Physics 3 0 0 3 3. PTGE 9261 Environmental Science and Engineering 3 0 0 3 4. PTEC 9151 Electron Devices 3 0 0 3 5. PTEC 9152 Circuit Analysis 3 1 0 4 TOTAL 15 2 0 17 SEMESTER II COURSE S.NO. COURSE TITLE L T P C CODE THEORY 1. PTMA 9212 Tran sforms and Partial Differential Equations 3 1 0 4 2. PTEC 9201 Electromagnetic Fields and Waves 3 0 0 3 3. PTEC 9202 Electronic Circuits- I 3 0 0 3 4. PTEC 9203 Signals and Systems 3 1 0 4 PRACTICAL 5. PTEC 9204 Electronic Circuits Lab 0 0 3 2 TOTAL 12 2 3 16 SEMESTER III S.NO. CODE NO. COURSE TITLE L T P C THEORY 1. PTEC 9251 Digital Electronics and System Design 3 1 0 4 2. PTEC 9252 Electronic Circuits- II 3 1 0 4 3. PTEC 9253 Communication Systems 3 0 0 3 4. PTEC 9254 Control Systems 3 1 0 4 PRACTICAL 5. PTEC 9257 Digital System Lab 0 0 3 2 TOTAL 12 3 3 17 1 SEMESTER IV COURSE S.NO. COURSE TITLE L T P C CODE THEORY 1. PTEC 9301 Digital Communication Techniques 3 0 0 3 2. PTEC 9302 Linear Integrated Circuits 3 0 0 3 3.
    [Show full text]
  • 6.453 Quantum Optical Communication Reading 4
    Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.453 Quantum Optical Communication Lecture Number 4 Fall 2016 Jeffrey H. Shapiro c 2006, 2008, 2014, 2016 Date: Tuesday, September 20, 2016 Reading: For the quantum harmonic oscillator and its energy eigenkets: C.C. Gerry and P.L. Knight, Introductory Quantum Optics (Cambridge Uni- • versity Press, Cambridge, 2005) pp. 10{15. W.H. Louisell, Quantum Statistical Properties of Radiation (McGraw-Hill, New • York, 1973) sections 2.1{2.5. R. Loudon, The Quantum Theory of Light (Oxford University Press, Oxford, • 1973) pp. 128{133. Introduction In Lecture 3 we completed the foundations of Dirac-notation quantum mechanics. Today we'll begin our study of the quantum harmonic oscillator, which is the quantum system that will pervade the rest of our semester's work. We'll start with a classical physics treatment and|because 6.453 is an Electrical Engineering and Computer Science subject|we'll develop our results from an LC circuit example. Classical LC Circuit Consider the undriven LC circuit shown in Fig. 1. As in Lecture 2, we shall take the state variables for this system to be the charge on its capacitor, q(t) Cv(t), and the flux through its inductor, p(t) Li(t). Furthermore, we'll consider≡ the behavior of this system for t 0 when one≡ or both of the initial state variables are non-zero, i.e., q(0) = 0 and/or≥p(0) = 0. You should already know that this circuit will then undergo simple6 harmonic motion,6 i.e., the energy stored in the circuit will slosh back and forth between being electrical (stored in the capacitor) and magnetic (stored in the inductor) as the voltage and current oscillate sinusoidally at the resonant frequency ! = 1=pLC.
    [Show full text]
  • ANNA UNIVERSITY, CHENNAI UNIVERSITY DEPARTMENTS B.E. BIOMEDICAL ENGINEERING REGULATIONS – 2019 VISION the Department of ECE Sh
    ANNA UNIVERSITY, CHENNAI UNIVERSITY DEPARTMENTS B.E. BIOMEDICAL ENGINEERING REGULATIONS – 2019 VISION The Department of ECE shall strive continuously to create highly motivated, technologically competent engineers, be a benchmark and a trend setter in Electronics and Communication Engineering by imparting quality education with interwoven input from academic institutions, research organizations and industries, keeping in phase with rapidly changing technologies imbibing ethical values. MISSION Imparting quality technical education through flexible student centric curriculum evolved continuously for students of ECE with diverse backgrounds. Providing good academic ambience by adopting best teaching and learning practices. Providing congenial ambience in inculcating critical thinking with a quest for creativity, innovation, research and development activities. Enhancing collaborative activities with academia, research institutions and industries by nurturing ethical entrepreneurship and leadership qualities. Nurturing continuous learning in the stat-of-the-art technologies and global outreach programmes resulting in competent world class engineers. ANNA UNIVERSITY, CHENNAI UNIVERSITY DEPARTMENTS REGULATIONS - 2019 CHOICE BASED CREDIT SYSTEM B.E. BIO MEDICAL ENGINEERING The programme spells out Programme Educational Objectives (6 PEOs), Programme Outcomes (12 POs) with mapping and Program Specific Outcomes (4 PSOs) 1. PROGRAM EDUCATIONAL OBJECTIVES (PEOs) THE OBJECTIVES OF THE B.E BIO MEDICAL ENGINEERING PROGRAMME IS BROADLY DEFINED ON THE FOLLOWING: I. Prepare the students to comprehend the fundamental concepts in Bio Medical Engineering. II. Enable the students to relate theory with practice for problem solving. III. Enable the students to critically analyse the present trends and learn and understand future issues. IV. Motivate the students to continue to pursue lifelong learning as professional engineers and scientists and effectively communicate.
    [Show full text]
  • Quantum Memristors
    UC San Diego UC San Diego Previously Published Works Title Quantum memristors. Permalink https://escholarship.org/uc/item/9cb4k842 Journal Scientific reports, 6(1) ISSN 2045-2322 Authors Pfeiffer, P Egusquiza, IL Di Ventra, M et al. Publication Date 2016-07-06 DOI 10.1038/srep29507 Peer reviewed eScholarship.org Powered by the California Digital Library University of California www.nature.com/scientificreports OPEN Quantum memristors P. Pfeiffer1, I. L. Egusquiza2, M. Di Ventra3, M. Sanz1 & E. Solano1,4 Technology based on memristors, resistors with memory whose resistance depends on the history of the crossing charges, has lately enhanced the classical paradigm of computation with neuromorphic architectures. However, in contrast to the known quantized models of passive circuit elements, such Received: 22 March 2016 as inductors, capacitors or resistors, the design and realization of a quantum memristor is still missing. Here, we introduce the concept of a quantum memristor as a quantum dissipative device, whose Accepted: 17 June 2016 decoherence mechanism is controlled by a continuous-measurement feedback scheme, which accounts Published: 06 July 2016 for the memory. Indeed, we provide numerical simulations showing that memory effects actually persist in the quantum regime. Our quantization method, specifically designed for superconducting circuits, may be extended to other quantum platforms, allowing for memristor-type constructions in different quantum technologies. The proposed quantum memristor is then a building block for neuromorphic quantum computation and quantum simulations of non-Markovian systems. Although they are often misused terms, the difference between information storage and memory is relevant. While the former refers to saving information in a physical device for a future use without changes, a physical sys- tem shows memory when its dynamics, usually named non-Markovian1,2, depend on the past states of the system.
    [Show full text]
  • BE ECE Sem8.Pdf
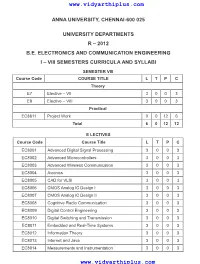
    www.vidyarthiplus.com ANNA UNIVERSITY, CHENNAI-600 025 UNIVERSITY DEPARTMENTS R – 2012 B.E. ELECTRONICS AND COMMUNICATION ENGINEERING I – VIII SEMESTERS CURRICULA AND SYLLABI SEMESTER VIII Course Code COURSE TITLE L T P C Theory E7 Elective – VII 3 0 0 3 E8 Elective – VIII 3 0 0 3 Practical EC8811 Project Work 0 0 12 6 Total 6 0 12 12 E LECTIVES Course Code Course Title L T P C EC8001 Advanced Digital Signal Processing 3 0 0 3 EC8002 Advanced Microcontrollers 3 0 0 3 EC8003 Advanced Wireless Communication 3 0 0 3 EC8004 Avionics 3 0 0 3 EC8005 CAD for VLSI 3 0 0 3 EC8006 CMOS Analog IC Design I 3 0 0 3 EC8007 CMOS Analog IC Design II 3 0 0 3 EC8008 Cognitive Radio Communication 3 0 0 3 EC8009 Digital Control Engineering 3 0 0 3 EC8010 Digital Switching and Transmission 3 0 0 3 EC8011 Embedded and Real-Time Systems 3 0 0 3 EC8012 Information Theory 3 0 0 3 EC8013 Internet and Java 3 0 0 3 EC8014 Measurements and Instrumentation 3 0 0 3 www.vidyarthiplus.com www.vidyarthiplus.com EC8015 Medical Electronics 3 0 0 3 EC8016 Microwave Engineering 3 0 0 3 EC8017 Parallel and Distributed processing 3 0 0 3 EC8018 RF Microelectronics 3 0 0 3 EC8019 Satellite Communication 3 0 0 3 EC8020 Speech Processing 3 0 0 3 EC8021 VLSI Signal Processing 3 0 0 3 EC8022 Wireless Networks 3 0 0 3 EC8071 Cryptography and Network Security 3 0 0 3 EC8072 Electro Magnetic Interference and Compatibility 3 0 0 3 EC8073 Foundations for Nano-Electronics 3 0 0 3 EC8074 Multimedia Compression and Communication 3 0 0 3 EC8075 Robotics 3 0 0 3 EC8076 Soft Computing and
    [Show full text]
  • Superconducting Quantum Circuits Theory and Application
    UNIVERSITY OF CALIFORNIA, MERCED Superconducting quantum circuits theory and application by Xiuhao Deng A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Physics Committee in charge: Professor Kevin Mitchell, Chair Professor Raymond Chiao Professor Jay Sharping Professor Chih-Chun Chien Professor Boaz Ilan Spring 2015 c 2015 Xiuhao Deng All rights are reserved. The dissertation of Xiuhao Deng is approved: Kevin Mitchell, Chair Date Raymond Chiao Date Jay Sharping Date Chih-Chun Chien Date Boaz Ilan Date University of California, Merced c Spring 2015 To my parents iv Acknowledgments First of all, I would like to sincerely thank my advisor Professor Raymond Chiao. Two years ago, when I was very frustrated, he gave me a lot of helpful advice and inspiration. He encouraged me to do what I am interested in. His enthusiasm in scientific research is like a lighthouse guiding me. Finally I am finishing this Ph.D. program, I have so many thanks to give for all of his help. Wish Ray sincerely for the best and a good health. Thank professor Chih-Chun Chien for advising me. He is always nice and patient for discussion and answering my questions. He also gave me a lot of thoughtful suggestions for my career and study. I enjoy a lot working with him for recent projects. Thank all the committee. Especially, professor Kevin Mitchell has been my committee member since 2010. I am so glad to have him as my committee chair for knowing my stories and what I have been working on since the beginning.
    [Show full text]
  • B.E. Electronics and Communication Engineering
    ANNA UNIVERSITY, CHENNAI 600 025 UNIVERSITY DEPARTMENTS R- 2013 B.E. (PART TIME) ELECTRONICS AND COMMUNICATION ENGINEERING I – VII SEMESTERS CURRICULUM AND SYLLABUS SEMESTER I COURSE S.NO COURSE TITLE L T P C CODE THEORY 1. PTMA8151 Applied Mathematics 3 0 0 3 2. PTPH8152 Physics for Electrical and Electronics 3 0 0 3 Engineering 3. PTCY8151 Chemistry for Electrical and Electronics 3 0 0 3 Engineering 4. PTEC8101 Circuit Theory 3 0 0 3 5. PTEC8102 Electronic Devices 3 0 0 3 TOTAL 15 0 0 15 SEMESTER II COURSE S.NO. COURSE TITLE L T P C CODE THEORY 1. PTEC8201 Digital Electronics and System Design 3 0 0 3 2. PTEC8202 Electronic Circuits – I 3 0 0 3 3. PTEC8203 Signals and Systems 3 0 0 3 4. PTMA8253 Transforms and Partial Differential Equations 3 0 0 3 PRACTICAL 5. PTEC8211 Electronic circuits – I Laboratory 0 0 3 2 TOTAL 12 0 3 14 SEMESTER III COURSE S.NO. COURSE TITLE L T P C CODE THEORY 1. PTEC8301 Communication Theory 3 0 0 3 2. PTEC8302 Electromagnetic Fields and Waves 3 0 0 3 3. PTEC8303 Electronic Circuits – II 3 0 0 3 4. Operational Amplifiers and Analog Integrated PTEC8304 3 0 0 3 Circuits PRACTICAL 5. PTEC8311 Electronic circuits – II Laboratory 0 0 3 2 TOTAL 12 0 3 14 1 SEMESTER IV COURSE S.NO. COURSE TITLE L T P C CODE THEORY 1. PTEC8401 Digital Communication Techniques 3 0 0 3 2. PTEC8402 Discrete Time Signal Processing 3 0 0 3 3.
    [Show full text]
  • The Dual Canonical Formalism in the Quantum Junction Systems
    THE DUAL CANONICAL FORMALISM IN THE QUANTUM JUNCTION SYSTEMS MORISHIGE YONEDA∗,MASAAKI NIWA† AND MITSUYA MOTOHASHI‡ We have constructed a theory of dual canonical formalism, to study the quantum dual systems. In such a system, as the relationship between current and voltage of each, we assumed the duality conditions. As a simple example, we examined the duality between the SC(superconductor)/SI(superinsulator)/SC(superconductor) junction and its reverse SI/SC/SI junction. We derived the relationship between the phase and the number of particles in a dual system of each other. Keywords:duality, quantum junction systems, SC/SI/SC junction, SI/SC/SI junction 1 Introduction The duality has been known to be a powerful tool in various physical systems such as statistical mechanics[1] and field theory[2],[3]. Furthermore, the duality has been also known in several studies of the Josephson junction systems[4],[5].In superconducting systems, the general Josephson junction are known as the quan- tum effect devices[6],[7] which operates by using the Cooper-pair tunneling. Fur- thermore, the mesoscopic Josephson junction can be used as a quantum effect devices which operates by using the single Cooper-pair tunneling created by a Coulomb blockade[8]. In contrast, the mesoscopic dual Josephson junction systems are known as the quantum effect devices which operates by using the single quantum vortex(quantum flux) tunneling[9]. The Cooper-pair and the quantum vortex are known as the duality relation to each other[10],[11]. That is, under certain conditions, even if we replace the role of Cooper pairs and vortices, these systems satisfy the equation of similar type.
    [Show full text]
  • BE-Biomedical-Engineering-2018.Pdf
    B.E Biomedical Engineering Curriculum and Syllabus Effective from the Academic year 2018 - 2019 Department of Biomedical Engineering School of Engineering VISION OF THE DEPARTMENT To be a premiere in Biomedical Engineering field by imparting technical knowledge and nurture talents with strong research focus towards betterment of healthy nation. MISSION OF THE DEPARTMENT M1. To provide quality education in Biomedical Engineering by effective teaching learning process and inculcating value-based education. M2. To incorporate collaborative research with institution, hospitals and health care industry to bring out leadership and professionalism. M3. Encourage to explore innovative ideas to create enabling technologies to improve healthcare technologies. M4. Exhibit societal and ethical values, teamwork spirit, multidisciplinary approach for successful careers globally, as entrepreneurs and to engage in lifelong learning. PROGRAM SPECIFIC OUTCOMES (PEO) The Graduates of the B.E biomedical engineering within few years will be PEO 1: Engaged in professional practise as biomedical engineers/related positions in industry, academia, hospital and government sectors. PEO 2: Continuing towards professional development in biomedical engineering or other related fields by successfully engaging in post graduate education, scientific research, entrepreneurship throughout their careers. PEO 3: Utilizing Engineering knowledge in creating innovative solutions or enabling technologies for the betterment of healthcare society PEO 4: Exhibiting leadership and
    [Show full text]
  • Anna University, Chennai University Departments B.E. Electronics and Communication Engineering Regulations – 2019 Vision
    ANNA UNIVERSITY, CHENNAI UNIVERSITY DEPARTMENTS B.E. ELECTRONICS AND COMMUNICATION ENGINEERING REGULATIONS – 2019 VISION The Department of ECE shall strive continuously to create highly motivated, technologically competent engineers, be a benchmark and a trend setter in Electronics and Communication Engineering by imparting quality education with interwoven input from academic institutions, research organizations and industries, keeping in phase with rapidly changing technologies imbibing ethical values. MISSION Imparting quality technical education through flexible student centric curriculum evolved continuously for students of ECE with diverse backgrounds. Providing good academic ambience by adopting best teaching and learning practices. Providing congenial ambience in inculcating critical thinking with a quest for creativity, innovation, research and development activities. Enhancing collaborative activities with academia, research institutions and industries by nurturing ethical entrepreneurship and leadership qualities. Nurturing continuous learning in the stat-of-the-art technologies and global outreach programmes resulting in competent world class engineers. 1 ANNA UNIVERSITY, CHENNAI UNIVERSITY DEPARTMENTS B.E. ELECTRONICS AND COMMUNICATION ENGINEERING REGULATIONS – 2019 The Programme defines Programme Educational Objectives, Programme Outcomes and Programme Specific Outcomes as follows: 1. PROGRAMME EDUCATIONAL OBJECTIVES (PEOs): PEO1 Equip the students with sufficient theoretical, analytical and initiative skills in Basic Sciences and Engineering necessary, to assimilate, analyze, synthesis and innovate solutions to meet societal needs. PEO2 To provide adequate research ambience enabling the students to inculcate thirst for life long learning and sustained research interest. PEO3 To instill and practice values, leadership qualities and team spirit to promote entrepreneurship and indigenization. After the course duration of four years, B.E. graduates of Electronics and Communication Engineering will exhibit the following outcomes: 2.
    [Show full text]
  • 6.453 Quantum Optical Communication Spring 2009
    MIT OpenCourseWare http://ocw.mit.edu 6.453 Quantum Optical Communication Spring 2009 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.453 Quantum Optical Communication Lecture Number 4 Fall 2008 Jeffrey H. Shapiro c 2006, 2008 � Date: Tuesday, September 16, 2008 Reading: For the quantum harmonic oscillator and its energy eigenkets: C.C. Gerry and P.L. Knight, Introductory Quantum Optics (Cambridge Uni­ • versity Press, Cambridge, 2005) pp. 10–15. W.H. Louisell, Quantum Statistical Properties of Radiation (McGraw-Hill, New • York, 1973) sections 2.1–2.5. R. Loudon, The Quantum Theory of Light (Oxford University Press, Oxford, • 1973) pp. 128–133. Introduction In Lecture 3 we completed the foundations of Dirac-notation quantum mechanics. Today we’ll begin our study of the quantum harmonic oscillator, which is the quantum system that will pervade the rest of our semester’s work. We’ll start with a classical physics treatment and—because 6.453 is an Electrical Engineering and Computer Science subject—we’ll develop our results from an LC circuit example. Classical LC Circuit Consider the undriven LC circuit shown in Fig. 1. As in Lecture 2, we shall take the state variables for this system to be the charge on its capacitor, q(t) = Cv(t), and the flux through its inductor, p(t) Li(t). Furthermore, we’ll consider the behavior of this system for t 0 when one ≡or both of the initial state variables are non-zero, i.e., q(t) = 0 and/or≥ p(0) = 0.
    [Show full text]