Cell Motility Driven by Actin Polymerization
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Glossary - Cellbiology
1 Glossary - Cellbiology Blotting: (Blot Analysis) Widely used biochemical technique for detecting the presence of specific macromolecules (proteins, mRNAs, or DNA sequences) in a mixture. A sample first is separated on an agarose or polyacrylamide gel usually under denaturing conditions; the separated components are transferred (blotting) to a nitrocellulose sheet, which is exposed to a radiolabeled molecule that specifically binds to the macromolecule of interest, and then subjected to autoradiography. Northern B.: mRNAs are detected with a complementary DNA; Southern B.: DNA restriction fragments are detected with complementary nucleotide sequences; Western B.: Proteins are detected by specific antibodies. Cell: The fundamental unit of living organisms. Cells are bounded by a lipid-containing plasma membrane, containing the central nucleus, and the cytoplasm. Cells are generally capable of independent reproduction. More complex cells like Eukaryotes have various compartments (organelles) where special tasks essential for the survival of the cell take place. Cytoplasm: Viscous contents of a cell that are contained within the plasma membrane but, in eukaryotic cells, outside the nucleus. The part of the cytoplasm not contained in any organelle is called the Cytosol. Cytoskeleton: (Gk. ) Three dimensional network of fibrous elements, allowing precisely regulated movements of cell parts, transport organelles, and help to maintain a cell’s shape. • Actin filament: (Microfilaments) Ubiquitous eukaryotic cytoskeletal proteins (one end is attached to the cell-cortex) of two “twisted“ actin monomers; are important in the structural support and movement of cells. Each actin filament (F-actin) consists of two strands of globular subunits (G-Actin) wrapped around each other to form a polarized unit (high ionic cytoplasm lead to the formation of AF, whereas low ion-concentration disassembles AF). -

Marine Microplankton Ecology Reading
Marine Microplankton Ecology Reading Microbes dominate our planet, especially the Earth’s oceans. The distinguishing feature of microorganisms is their small size, usually defined as less than 200 micrometers (µm); they are all invisible to the naked eye. As a group, sea microbes are extremely diverse, and extremely versatile with respect to their abilities to make and eat food. All marine microbes are too small to swim against the current and are therefore classified as plankton. First we will discuss several ways to classify marine microbes. 1. Size Planktonic marine organisms can be divided into the following size categories: Category Size femtoplankton <0.2 µm picoplankton 0.2-2 µm nanoplankton 2-20 µm microplankton 20-200 µm mesoplankton 200-2000 µm In this laboratory we are concerned with the microscopic portion of the plankton, less than 200 µm. These organisms are not visible to the naked eye (Figure 1). Figure 1. Size classes of marine plankton 2. Type A. Viruses Viruses are the smallest and simplest microplankton. They range from 0.01 to 0.3 um in diameter. Externally, viruses have a capsid, or protein coat. Viruses can also have simple or complex external morphologies with tail fibers and structures that are used to inject DNA or RNA into their host. Viruses have little internal morphology. They do not have a nucleus or organelles. They do not have chlorophyll. Inside a virus there is only nucleic acid, either DNA or RNA. Viruses do not grow and have no metabolism. Marine viruses are highly abundant. There are up to 10 billion in one liter of seawater! B. -

Gastrointestinal Motility Physiology
GASTROINTESTINAL MOTILITY PHYSIOLOGY JAYA PUNATI, MD DIRECTOR, PEDIATRIC GASTROINTESTINAL, NEUROMUSCULAR AND MOTILITY DISORDERS PROGRAM DIVISION OF PEDIATRIC GASTROENTEROLOGY AND NUTRITION, CHILDREN’S HOSPITAL LOS ANGELES VRINDA BHARDWAJ, MD DIVISION OF PEDIATRIC GASTROENTEROLOGY AND NUTRITION CHILDREN’S HOSPITAL LOS ANGELES EDITED BY: CHRISTINE WAASDORP HURTADO, MD REVIEWED BY: JOSEPH CROFFIE, MD, MPH NASPGHAN PHYSIOLOGY EDUCATION SERIES SERIES EDITORS: CHRISTINE WAASDORP HURTADO, MD, MSCS, FAAP [email protected] DANIEL KAMIN, MD [email protected] CASE STUDY 1 • 14 year old female • With no significant past medical history • Presents with persistent vomiting and 20 lbs weight loss x 3 months • Initially emesis was intermittent, occurred before bedtime or soon there after, 2-3 hrs after a meal • Now occurring immediately or up to 30 minutes after a meal • Emesis consists of undigested food and is nonbloody and nonbilious • Associated with heartburn and chest discomfort 3 CASE STUDY 1 • Initial screening blood work was unremarkable • A trial of acid blockade was started with improvement in heartburn only • Antiemetic therapy with ondansetron showed no improvement • Upper endoscopy on acid blockade was normal 4 CASE STUDY 1 Differential for functional/motility disorders: • Esophageal disorders: – Achalasia – Gastroesophageal Reflux – Other esophageal dysmotility disorders • Gastric disorders: – Gastroparesis – Rumination syndrome – Gastric outlet obstruction : pyloric stricture, pyloric stenosis • -
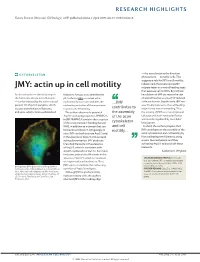
JMY: Actin up in Cell Motility Migrate Faster in a Wound Healing Assay That Assesses Cell Motility
RESEARCH HIGHLIGHTS Nature Reviews Molecular Cell Biology | AOP, published online 2 April 2009; doi:10.1038/nrm2678 — the area closest to the direction CYTOSKELETON of movement — in motile cells. This suggests a role for JMY in cell motility. Indeed, cells that overexpress JMY JMY: actin up in cell motility migrate faster in a wound healing assay that assesses cell motility. By contrast, Actin nucleation — the initial step in filaments. A study now identifies the knockdown of JMY decreases the rate the formation of new actin filaments p53 cofactor JMY as a novel actin of wound healing as a result of reduced — can be induced by the actin-related nucleation factor that combines the ...JMY actin nucleation. Significantly, JMY was protein 2/3 (Arp2/3) complex, which nucleating activities of these proteins specifically induced to the cell leading creates branched actin filaments, to promote cell motility. contributes to edge in response to wounding. Thus, and spire, which creates unbranched The authors observed a potential the assembly the activity of JMY as a transcriptional Arp2/3-activating sequence, WWWCA, of the actin cofactor and actin nucleation factor in JMY. WWWCA contains three repeats seems to be regulated by its cellular of the actin monomer-binding domain cytoskeleton localization. WH2, in addition to a domain that can and cell In short, the authors propose that bind actin and Arp2/3. Intriguingly, in motility... JMY contributes to the assembly of the vitro, JMY can both activate Arp2/3 and, actin cytoskeleton and cell motility by in the absence of Arp2/3, induce rapid first nucleating new filaments, using actin polymerization. -

The Effect of Azide on Phototaxis in Chlamydomonas Reinhardi (Motility)
Proc. Nat. Acad. Sci. USA Vol. 71, No. 5, pp. 1824-1827, May 1974 The Effect of Azide on Phototaxis in Chlamydomonas reinhardi (motility) ROBERT L. STAVIS Department of Molecular Biology, Division of Biological Sciences, Albert Einstein College of Medicine, Bronx, New York 10461 Communicated by Alfred Gilman, February 25, 1974 ABSTRACT Phototaxis in Chlamydomonas reinhardi section of a cuvette. The maximum rate of accumulation was specifically inhibited by azide. The effect of azide was divided by the concentration of cells rapid and reversible, and did not depend upon the intensity .(AOD8wo/min) (ODwo) of actinic light. Under conditions of completely inhibited is the phototaxis coefficient, a measure of phototaxis indepen- phototaxis, azide had no effect on the number of motile dent of cell density. The actinic light used in these studies was cells in the population or on the rate of motility. The an Osram 150-W xenon lamp in an Oriel 6137 lamp housing effect was not related to changes in oxygen uptake or (Oriel Corp. of America, Stamford, Conn.). Light below 350 cellular ATP concentration. Apparently, a cellular com- ponent or process specifically involved in phototaxis is nm or above 650 nm was excluded by filtering the light source inactivated by azide. with an Oriel C-722-3900 long-pass filter, a G-774-4450 band-pass filter, and a G-776-7100 infrared-absorbing filter. The stimulus-response system that mediates the tactic be- The resulting light had a maximum intensity at 445 nm, with havior of microorganisms may be thought of as consisting a half-maximum band width of about 100 nm and an intensity of components that function as stimulus receptor, a transmis- of about 100 J/m2 per see at the phototaxis cuvette. -

Actin-Based Motility of Pathogenic Bacteria
Journal of Cell Science 112, 1697-1708 (1999) 1697 Printed in Great Britain © The Company of Biologists Limited 1999 JCS9942 A comparative study of the actin-based motilities of the pathogenic bacteria Listeria monocytogenes, Shigella flexneri and Rickettsia conorii E. Gouin1, H. Gantelet1, C. Egile2, I. Lasa1,*, H. Ohayon3, V. Villiers1, P. Gounon3, P. J. Sansonetti2 and P. Cossart1,‡ 1Unité des Interactions Bactéries-Cellules, 2Unité de Pathogénie Microbienne Moléculaire, 3Station Centrale de Microscopie Electronique, Institut Pasteur, 25 and 28 Rue du Dr Roux, 75724 Paris Cedex 15, France *Present address: Dpto. Producción agraria, Universidad Pública de Navarra, Campus de Arrosadia s/n, Pamplona-31006, Spain ‡Author for correspondence (e-mail: [email protected]) Accepted 17 March; published on WWW 11 May 1999 SUMMARY Listeria monocytogenes, Shigella flexneri, and Rickettsia of actin with the S1 subfragment of myosin in infected cells conorii are three bacterial pathogens that are able to showed that the comet tails of Rickettsia have a structure polymerize actin into ‘comet tail’ structures and move strikingly different from those of L. monocytogenes or S. within the cytosol of infected cells. The actin-based flexneri. In Listeria and Shigella tails, actin filaments form motilities of L. monocytogenes and S. flexneri are known to a branching network while Rickettsia tails display longer require the bacterial proteins ActA and IcsA, respectively, and not cross-linked actin filaments. Immunofluorescence and several mammalian cytoskeleton proteins including studies revealed that the two host proteins, VASP and α- the Arp2/3 complex and VASP (vasodilator-stimulated actinin colocalized with actin in the tails of Rickettsia but phosphoprotein) for L. -

Microbial Motility in 3-D Extending the Reach of Phase Contrast Microscopy to Track the Three- Dimensional Motility of Microbes from Woods Hole, MA
Microbial Motility in 3-D Extending the reach of phase contrast microscopy to track the three- dimensional motility of microbes from Woods Hole, MA. Max Villa, Microbial Diversity 2016, Marine Biological Lab, Woods Hole, MA, Home Institution: Duke University, Durham, NC Abstract Bacteria solve complex 3D optimization problems to search for energy sources in oligotrophic environments. However, until now, accessing their 3D motility patterns has been limited to expensive and complex microscopy systems. Herein, a recent algorithm that using the diffraction patterns of out-of-focus bacteria to determine their Z-location is implemented and applied to a diverse collection of marine bacteria isolated from around Woods Hole, MA. Introduction We fundamentally rely on the concept of search. Google, Yahoo, Baidu and others have made search a modern necessity and changed our vernacular (“you can google it”). Microbial chemo- and phototaxis (“search”) in oligotrophic marine environments is essential to survival and to our understanding of how microbes influence the ecology of their environment. Patterns of microbial motility can help us better understand how bacteria sense and respond to chemical cues in their microenvironment.1,2, 3 Studying motility in the context of populations can provide insights into variations in their behavior across the population, so-called ‘bacterial individuality’.4,5 Finally, few models exist to quantitatively connect genetics to behavior. 6 High throughput tracking of bacteria is an ideal system for efficiently producing large datasets to probe the connection between behavior and genetics. A deep understanding of diverse microbial motility should lead to more predictive models of how microbes shape our environment. -

Molecular Marine Microbiology
J. Molec. Microbiol. Biotechnol. (1999) 1(1): 3-4. JMMBMarine Symposium Microbiology 3 Molecular Marine Microbiology Douglas H. Bartlett* describes the bacterial manufacturing of magnetic iron containing organelles (magnetosomes) within certain Center for Marine Biotechnology and Biomedicine benthic bacteria and their biotechnological promise in Scripps Institution of Oceanography products ranging from magnetic tapes to magnetic University of California, San Diego resonance imaging devices. La Jolla, CA 92093-0202, USA Two articles deal with mysterious motility mechanisms operating in marine microbes. Linda McCarter introduces surface-regulated phenomena, including swarming motility The following thirteen minireviews introduce some of the via lateral flagella, in the human pathogen and marine exciting milestones being covered in molecular marine resident, V. parahaemolyticus. Bianca Brahamsha details microbiology today, and in many cases, their biomedical the only known case of liquid motility in the absence of or biotechnological relevance. The issues covered include flagella, a phenotype displayed by many marine quorum and anti-quorum sensing, selected symbioses, Synechococcus species. DNA shuffling in the environment, the evolution and devel- The minireviews end with descriptions of the opment of novel motility mechanisms, hydrocarbon deg- adaptations of certain deep-sea prokaryotes to extremes radation, the interactions of microbes with metals, and of pressure and temperature. Kato and Qureshi present a adaptations to extremes of pressure and temperature. Al- taxomonic overview of deep-sea bacteria and genetic and though most of these topics are not exclusive to marine biophysical analyses of respiratory chain adaptations to realms, they all have as a common thread a profound rel- elevated pressure. My article describes genetic evidence evance to the ocean environment. -

Normal Gastrointestinal Motility and Function Esophagus
Normal Gastrointestinal Motility and Function "Motility" is an unfamiliar word to many people; it is used primarily to describe the contraction of the muscles in the gastrointestinal tract. Because the gastrointestinal tract is a circular tube, when these muscles contract, they close off the tube or make the opening inside smaller - they squeeze. These muscles can contract in a synchronized way to move the food in one direction (usually downstream, but occasionally upstream for short distances); this is called peristalsis. If you looked at the intestine, you would see a ring of contraction that moves along pushing contents ahead of it. At other times, the muscles in adjacent parts of the gastrointestinal tract squeeze more or less independently of each other: this has the effect of mixing the contents but not moving them up or down. Both kinds of contraction patterns are called motility. The gastrointestinal tract is divided into four distinct parts: the esophagus, stomach, small intestine, and large intestine (colon). They are separated from each other by special muscles called sphincters which normally stay tightly closed and which regulate the movement of food and food residues from one part to another. Each part of the gastrointestinal tract has a unique function to perform in digestion, and as a result each part has a distinct type of motility and sensation. When motility or sensations are not appropriate for performing this function, they cause symptoms such as bloating, vomiting, constipation, or diarrhea which are associated with subjective sensations such as pain, bloating, fullness, and urgency to have a bowel movement. -

Bacterial Motility م.م رنا مشعل Bacterial Motility
Bacterial Motility م.م رنا مشعل Bacterial Motility The ability of an organism to move by itself is called motility. A large number of bacteria are motile. Most possess one or more flagella on their surface that allow them to swim. Bacterial flagella are tiny hair like organelles of locomotion. Originating in the cytoplasm beneath the cell wall, they extend beyond the cell, usually equaling or exceeding it in length. Their fine protein structure requires special staining techniques for demonstrating them with the light microscope. Site of Flagella The pattern of flagellation is an important feature in identification of motile bacteria. Monotrichous is a single polar flagellum. Amphitrichous one or more flagella at both poles. Lophotrichous tufts of flagella at one end pole. Peritrichous flagella surrounding the perimeter of the cell. • Bacterial Motility Flagella compose from: . Filament – Composed of a protein called flagellin . Hook – Base of filament near cell wall . Basal Body - Anchors filament & hook to cell wal Types of movement : . Run : straight line movement occurs when the flagella rotates couter clockwise. Tumbles : turning the direction by clockwise movement of the flagella. Flagella are anchored by pairs of rings associated with the plasma membrane and cell wall. Gram positive bacteria have only the inner pair of rings. Motility testing Motility could be detected by: 1) Hanging Drop technique. 2) Flagella stain. 3) Semi-Solid media Inoculation. 1) Hanging Drop slide The slide for a hanging drop is ground with a concave well in the centre; the cover glass holds a drop of the suspension. When the cover glass is inverted over the well of the slide, the drop hangs from the glass in the hollow concavity of the slide. -

Examination and Processing of Human Semen
WHO laboratory manual for the Examination and processing of human semen FIFTH EDITION WHO laboratory manual for the Examination and processing of human semen FIFTH EDITION WHO Library Cataloguing-in-Publication Data WHO laboratory manual for the examination and processing of human semen - 5th ed. Previous editions had different title : WHO laboratory manual for the examination of human semen and sperm-cervical mucus interaction. 1.Semen - chemistry. 2.Semen - laboratory manuals. 3.Spermatozoa - laboratory manuals. 4.Sperm count. 5.Sperm-ovum interactions - laboratory manuals. 6.Laboratory techniques and procedures - standards. 7.Quality control. I.World Health Organization. ISBN 978 92 4 154778 9 (NLM classifi cation: QY 190) © World Health Organization 2010 All rights reserved. Publications of the World Health Organization can be obtained from WHO Press, World Health Organization, 20 Avenue Appia, 1211 Geneva 27, Switzerland (tel.: +41 22 791 3264; fax: +41 22 791 4857; e-mail: [email protected]). Requests for permission to reproduce or translate WHO publications— whether for sale or for noncommercial distribution—should be addressed to WHO Press, at the above address (fax: +41 22 791 4806; e-mail: [email protected]). The designations employed and the presentation of the material in this publication do not imply the expres- sion of any opinion whatsoever on the part of the World Health Organization concerning the legal status of any country, territory, city or area or of its authorities, or concerning the delimitation of its frontiers or boundaries. Dotted lines on maps represent approximate border lines for which there may not yet be full agreement. The mention of specifi c companies or of certain manufacturers’ products does not imply that they are endorsed or recommended by the World Health Organization in preference to others of a similar nature that are not mentioned. -

The Two Motility Systems Ofmyxococcus Xanthus Show
Proc. Natl. Acad. Sci. USA Vol. 90, pp. 3378-3382, April 1993 Microbiology The two motility systems of Myxococcus xanthus show different selective advantages on various surfaces (gliding bacterium/swarming/fruiting/video microscopy) WENYUAN SHI AND DAVID R. ZUSMAN Department of Molecular and Cell Biology, 401 Barker Hall, University of California, Berkeley, CA 94720 Communicated by Horace A. Barker, January 8, 1993 (received for review August 26, 1992) ABSTRACT Myxococcus xanthus, a bacterium that forms In this paper, we report that A-motility and S-motility show fruiting bodies, moves by gliding motility utilizing dual motility different selective advantages on different surfaces: A-mo- systems that differ both genetically and morphologically [sys- tility allows cells to move better than S-motility on relatively tem A, having at least 21 genetic loci and moving mainly single firm and dry surfaces, whereas S-motility allows cells to cells, and system S, having at least 10 genetic loci and moving move much better on relatively soft and wet surfaces. These groups (rafts) of cells] [Hodgkin, J. & Kaiser, D. (1979) Mol. results show that, like flagellated bacteria, the dual motility Gen. Genet. 172, 177-191]. In this study, we found that A- and systems in gliding bacteria allow cells to adapt to a variety of S-gliding-motility systems have different selective advantages physiological and ecological environments. on surfaces containing different concentrations of agar. We observed that colonies of A+S- cells (A-motile cells) swarmed better than A-S+ cells (S-motile cells) on relatively firm and MATERIALS AND METHODS dry surfaces (e.g., 1.5% agar).