Reinforcement Learning in Self Organizing Cellular Networks
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Long-Term Data Traffic Forecasting for Network Dimensioning in LTE With
electronics Article Long-Term Data Traffic Forecasting for Network Dimensioning in LTE with Short Time Series Carolina Gijón * , Matías Toril , Salvador Luna-Ramírez , María Luisa Marí-Altozano and José María Ruiz-Avilés Instituto de Telecomunicaciones (TELMA), Universidad de Málaga, CEI Andalucía TECH, 29071 Málaga, Spain; [email protected] (M.T.); [email protected] (S.L.-R.); [email protected] (M.L.M.-A.); [email protected] (J.M.R.-A.) * Correspondence: [email protected] Abstract: Network dimensioning is a critical task in current mobile networks, as any failure in this process leads to degraded user experience or unnecessary upgrades of network resources. For this purpose, radio planning tools often predict monthly busy-hour data traffic to detect capacity bottle- necks in advance. Supervised Learning (SL) arises as a promising solution to improve predictions obtained with legacy approaches. Previous works have shown that deep learning outperforms classical time series analysis when predicting data traffic in cellular networks in the short term (sec- onds/minutes) and medium term (hours/days) from long historical data series. However, long-term forecasting (several months horizon) performed in radio planning tools relies on short and noisy time series, thus requiring a separate analysis. In this work, we present the first study comparing SL and time series analysis approaches to predict monthly busy-hour data traffic on a cell basis in a live LTE network. To this end, an extensive dataset is collected, comprising data traffic per cell for a whole country during 30 months. The considered methods include Random Forest, different Citation: Gijón, C.; Toril, M.; Neural Networks, Support Vector Regression, Seasonal Auto Regressive Integrated Moving Average Luna-Ramírez, S.; Marí-Altozano, and Additive Holt–Winters. -

Modeling the Use of an Airborne Platform for Cellular Communications Following Disruptions
Dissertations and Theses 9-2017 Modeling the Use of an Airborne Platform for Cellular Communications Following Disruptions Stephen John Curran Follow this and additional works at: https://commons.erau.edu/edt Part of the Aviation Commons, and the Communication Commons Scholarly Commons Citation Curran, Stephen John, "Modeling the Use of an Airborne Platform for Cellular Communications Following Disruptions" (2017). Dissertations and Theses. 353. https://commons.erau.edu/edt/353 This Dissertation - Open Access is brought to you for free and open access by Scholarly Commons. It has been accepted for inclusion in Dissertations and Theses by an authorized administrator of Scholarly Commons. For more information, please contact [email protected]. MODELING THE USE OF AN AIRBORNE PLATFORM FOR CELLULAR COMMUNICATIONS FOLLOWING DISRUPTIONS By Stephen John Curran A Dissertation Submitted to the College of Aviation in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy in Aviation Embry-Riddle Aeronautical University Daytona Beach, Florida September 2017 © 2017 Stephen John Curran All Rights Reserved. ii ABSTRACT Researcher: Stephen John Curran Title: MODELING THE USE OF AN AIRBORNE PLATFORM FOR CELLULAR COMMUNICATIONS FOLLOWING DISRUPTIONS Institution: Embry-Riddle Aeronautical University Degree: Doctor of Philosophy in Aviation Year: 2017 In the wake of a disaster, infrastructure can be severely damaged, hampering telecommunications. An Airborne Communications Network (ACN) allows for rapid and accurate information exchange that is essential for the disaster response period. Access to information for survivors is the start of returning to self-sufficiency, regaining dignity, and maintaining hope. Real-world testing has proven that such a system can be built, leading to possible future expansion of features and functionality of an emergency communications system. -

Global Systems Performance Analysis for Mobile Communications (Gsm) Using Cellular Network Codecs
GLOBAL SYSTEMS PERFORMANCE ANALYSIS FOR MOBILE COMMUNICATIONS (GSM) USING CELLULAR NETWORK CODECS MaphuthegoEtu Maditsi, Thulani Phakathi, Francis Lugayizi and MichaelEsiefarienrhe Department of Computer Science, North West University, Mahikeng, South Africa ABSTRACT Global System for Mobile Communications (GSM) is a cellular network that is popular and has been growing in recent years. It was developed to solve fragmentation issues of the first cellular system, and it addresses digital modulation methods, level of the network structure, and services. It is fundamental for organizations to become learning organizations to keep up with the technology changes for network services to be at a competitive level. A simulation analysisusing the NetSim tool in this paper is presented for comparing different cellular network codecsfor GSM network performance. Theseparameters such as throughput, delay, and jitter are analyzed for the quality of service provided by each network codec. Unicast application for the cellular network is modeled for different network scenarios. Depending on the evaluation and simulation, it was discovered that G.711, GSM_FR, and GSM-EFR performed better than the other codecs, and they are considered to be the best codecs for cellular networks.These codecs will be of best use to better the performance of the network in the near future. KEYWORDS GSM, CODECS, Cellular Network, G.711, GSM_FR, GSM-EFR. 1. INTRODUCTION Cellular Networks play an important role in most organizations in the Information Technology (IT) field and countries as it potentially improve the economic growth and it also contributes extremely to human development and employment. Mobile communication networks equally help in sharing and gathering information [1]. -

Road Traffic Estimation Using Cellular Network Signaling in Intelligent Transportation Systems
Road Traffic Estimation using Cellular Network Signaling in Intelligent Transportation Systems David Gundlegård and Johan M Karlsson Linköping University Post Print N.B.: When citing this work, cite the original article. Original Publication: David Gundlegård and Johan M Karlsson, Road Traffic Estimation using Cellular Network Signaling in Intelligent Transportation Systems, 2009, Wireless technologies in Intelligent Transportation Systems. Editors: Ming-Tuo Zhou, Yan Zhang and L. T. Yan. ISBN: 978-1-60741-588-6 Copyright: Nova Science Publishers https://www.novapublishers.com/ Postprint available at: Linköping University Electronic Press http://urn.kb.se/resolve?urn=urn:nbn:se:liu:diva-50734 In: Wireless Technologies in Intelligent Transportation Systems ISBN 978-1-60741-588-6 Editors: Ming-Tuo Zhou, Yan Zhang and L. T. Yan, pp. © 2009 Nova Science Publishers, Inc. Chapter 13 ROAD TRAFFIC ESTIMATION USING CELLULAR NETWORK SIGNALING IN INTELLIGENT TRANSPORTATION SYSTEMS David Gundlegård and Johan M Karlsson Department of Science and Technology Linköping University, 601 74 Norrköping ABSTRACT In the area of Intelligent Transportation Systems the introduction of wireless communications is reshaping the information distribution concept, and is one of the most important enabling technologies. The distribution of real-time traffic information, scheduling and route-guidance information is helping the transportation management systems in their strive to optimize the system. The communication required to transfer all this information is rather expensive in terms of transmission power, use of the scarce resources of frequencies and also the building of an infrastructure to support the transceivers. By using information that already exists and is exchanged within the infrastructures of the GSM and UMTS networks, a lot of the resource problems are solved. -
A Comprehensive Survey on Moving Networks
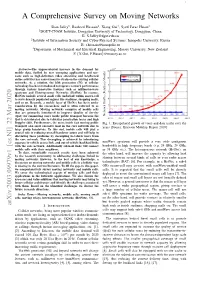
1 A Comprehensive Survey on Moving Networks Shan Jaffry1, Rasheed Hussain2, Xiang Gui3, Syed Faraz Hasan3 1DGUT-CNAM Institute, Dongguan University of Technology, Dongguan, China. E: [email protected] 2Institute of Information Security and Cyber-Physical Systems, Innopolis University, Russia E: [email protected] 3Department of Mechanical and Electrical Engineering, Massey University, New Zealand. E fX.Gui, [email protected] Abstract—The unprecedented increase in the demand for mobile data, fuelled by new emerging applications and use- cases such as high-definition video streaming and heightened online activities has caused massive strain on the existing cellular networks. As a solution, the fifth generation (5G) of cellular technology has been introduced to improve network performance through various innovative features such as millimeter-wave spectrum and Heterogeneous Networks (HetNet). In essence, HetNets include several small cells underlaid within macro-cell to serve densely populated regions like stadiums, shopping malls, and so on. Recently, a mobile layer of HetNet has been under consideration by the researchers and is often referred to as moving networks. Moving networks comprise of mobile cells that are primarily introduced to improve Quality of Service (QoS) for commuting users inside public transport because the QoS is deteriorated due to vehicular penetration losses and high Doppler shift. Furthermore, the users inside fast moving public Fig. 1: Extrapolated growth of voice and data traffic over the transport also exert excessive load on the core network due to years [Source: Ericsson Mobility Report 2018] large group handovers. To this end, mobile cells will play a crucial role in reducing overall handover count and will help in alleviating these problems by decoupling in-vehicle users from the core network. -

Gr Mbc 001 V1.1.1 (2018-06)
ETSI GR MBC 001 V1.1.1 (2018-06) GROUP REPORT Mobile Broadcast Convergence Group Report Disclaimer The present document has been produced and approved by the Mobile and Broadcast Convergence (MBC) ETSI Industry Specification Group (ISG) and represents the views of those members who participated in this ISG. It does not necessarily represent the views of the entire ETSI membership. 2 ETSI GR MBC 001 V1.1.1 (2018-06) Reference DGR/MBC-001 Keywords audio, broadband, broadcast, content, DVB, IMT, LTE-Advanced, mobile, multimedia, smartphone, UHDTV, video ETSI 650 Route des Lucioles F-06921 Sophia Antipolis Cedex - FRANCE Tel.: +33 4 92 94 42 00 Fax: +33 4 93 65 47 16 Siret N° 348 623 562 00017 - NAF 742 C Association à but non lucratif enregistrée à la Sous-Préfecture de Grasse (06) N° 7803/88 Important notice The present document can be downloaded from: http://www.etsi.org/standards-search The present document may be made available in electronic versions and/or in print. The content of any electronic and/or print versions of the present document shall not be modified without the prior written authorization of ETSI. In case of any existing or perceived difference in contents between such versions and/or in print, the only prevailing document is the print of the Portable Document Format (PDF) version kept on a specific network drive within ETSI Secretariat. Users of the present document should be aware that the document may be subject to revision or change of status. Information on the current status of this and other ETSI documents is available at https://portal.etsi.org/TB/ETSIDeliverableStatus.aspx If you find errors in the present document, please send your comment to one of the following services: https://portal.etsi.org/People/CommiteeSupportStaff.aspx Copyright Notification No part may be reproduced or utilized in any form or by any means, electronic or mechanical, including photocopying and microfilm except as authorized by written permission of ETSI. -

Download Activity Reports
UC Berkeley UC Berkeley Electronic Theses and Dissertations Title Towards Scalable Community Networks Permalink https://escholarship.org/uc/item/1zr87965 Author Hasan, Shaddi Publication Date 2019 Peer reviewed|Thesis/dissertation eScholarship.org Powered by the California Digital Library University of California Towards Scalable Community Networks by Shaddi Husein Hasan A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Computer Science in the Graduate Division of the University of California, Berkeley Committee in charge: Professor Eric Brewer, Chair Associate Professor Joshua Blumenstock Professor Scott Shenker Professor Anant Sahai Spring 2019 Towards Scalable Community Networks Copyright 2019 by Shaddi Husein Hasan 1 Abstract Towards Scalable Community Networks by Shaddi Husein Hasan Doctor of Philosophy in Computer Science University of California, Berkeley Professor Eric Brewer, Chair Over 400 million people live without access to basic communication services, largely in rural areas. Community-based networks, and particularly community cellular networks, can sustainably support services even in these extremely rural areas where traditional commercial network operators cannot. However, community cellular networks face a variety of technical, business, and regulatory challenges that hamper their proliferation. In this thesis, we aim to develop approaches to enable scale within and across community cellular networks. Through a mixed-methods study of more than 80 rural wireless Internet service providers, a related class of network operators, we identify key scaling challenges rural network operators face. We next present two approaches for addressing these challenges in the context of community cellular networks. The first, GSM Whitespaces, demonstrates that rural community cellular networks can safely share spectrum in bands occupied by incumbent mobile network operators, removing a key barrier to independent operation. -

Preferences of Smartphone Users in Mobile to Wi-Fi Data Traffic Offload
XXXIV Simpozijum o novim tehnologijama u poštanskom i telekomunikacionom saobraćaju – PosTel 2016, Beograd, 29. i 30. novembar 2016. PREFERENCES OF SMARTPHONE USERS IN MOBILE TO WI-FI DATA TRAFFIC OFFLOAD Siniša Husnjak, Ivan Forenbacher, Dragan Peraković, Marko Periša Faculty of Transport and Traffic Sciences, University of Zagreb, [email protected], [email protected], [email protected], [email protected] Abstract: Smartphone users generate data traffic using mobile and Wi-Fi access networks. The development of smartphones and the evolution of access networks has changed the behavior of smartphone users in generating data traffic. Data traffic offload is defined as a switch from the mobile to the Wi-Fi access network. Smartphone users offload large amounts of data traffic from mobile to Wi-Fi networks. This paper will show preferences of smartphone users that affect user's propensity and desire to offload data traffic from mobile to Wi-Fi networks. Keywords: smartphone, data traffic offload, mobile networks, Wi-Fi, user's preferences 1. Introduction Mobile data services are necessities for many smartphone users. Smartphones are bringing Internet experience to the mobile devices. According to [1], increased smartphone usage has changed consumers’ behavior, because it has encouraged and facilitated their need to be connected all the times. Average smartphone usage grew 43 % in 2015 and smartphones will cross four-fifths of generated mobile data traffic by 2020 [2]. In parallel, the use of Wi-Fi is exploding as more mobile devices are Wi-Fi enabled, the number of public hotspots expands and user acceptance grows [3]. Data traffic offload refers to traffic from dual-mode smartphones (i.e., supports cellular and Wi-Fi connectivity) over Wi-Fi networks. -

Traffic Volume Estimation Through Cellular Networks Handover Information
Traffic volume estimation through cellular networks handover information Demissie, Correia, Bento TRAFFIC VOLUME ESTIMATION THROUGH CELLULAR NETWORKS HANDOVER INFORMATION Merkebe Getachew Demissie, Civil Engineering Department, Coimbra University, Portugal, Email: [email protected] Gonçalo Homem de Almeida Correia, Civil Engineering Department, Coimbra University, Portugal, Email: [email protected] Carlos Lisboa Bento, Informatics Engineering Department, Coimbra University, Portugal, Email: [email protected] ABSTRACT Traffic management agencies carry out different types of traffic counts. Permanent traffic counter (PTC) is the preferred counter that provides traffic statistics throughout the year. Due to its expensive installation and maintenance costs, PTC has limited road network coverage; therefore, agencies choose to utilize sample traffic counts from seasonal traffic counter (STC). However, road network covered with STC lack continuous observation to update changes in traffic in a regular basis, which causes a series impediment to the effective use of active traffic management schemes. One way that has been tried to obtain complementary traffic information is the use of cellular networks. This paper presents a method for estimating hourly traffic volume through a combined use of average city-wide traffic volume and cellular networks handover information. To test this method, handover data were collected from cellular towers in Lisbon, Portugal, which are situated along the Eixo norte-sul itinerarios principais road. The traffic volumes were also obtained from traffic counters installed in the same road. First, we applied statistical analysis to investigate the relationship between vehicular and cellular traffic. Then, we built a multiple linear regression model. Results from statistical analysis proved that handover can be used as a proxy to detect vehicle movement. -

Assessment of Deep Learning Methodology for Self-Organizing 5G Networks
applied sciences Article Assessment of Deep Learning Methodology for Self-Organizing 5G Networks Muhammad Zeeshan Asghar * , Mudassar Abbas †, Khaula Zeeshan †, Pyry Kotilainen † and Timo Hämäläinen Faculty of Information Technology, University of Jyväskylä, 40014 Jyväskylä, Finland * Correspondence: muhammad.z.asghar@jyu.fi; Tel.: +358-504497760 † These authors contributed equally to this work. Received: 9 May 2019; Accepted: 12 July 2019; Published: 25 July 2019 Abstract: In this paper, we present an auto-encoder-based machine learning framework for self organizing networks (SON). Traditional machine learning approaches, for example, K Nearest Neighbor, lack the ability to be precisely predictive. Therefore, they can not be extended for sequential data in the true sense because they require a batch of data to be trained on. In this work, we explore artificial neural network-based approaches like the autoencoders (AE) and propose a framework. The proposed framework provides an advantage over traditional machine learning approaches in terms of accuracy and the capability to be extended with other methods. The paper provides an assessment of the application of autoencoders (AE) for cell outage detection. First, we briefly introduce deep learning (DL) and also shed light on why it is a promising technique to make self organizing networks intelligent, cognitive, and intuitive so that they behave as fully self-configured, self-optimized, and self-healed cellular networks. The concept of SON is then explained with applications of intrusion detection and mobility load balancing. Our empirical study presents a framework for cell outage detection based on an autoencoder using simulated data obtained from a SON simulator. Finally, we provide a comparative analysis of the proposed framework with the existing frameworks. -

Data Traffic Analysis and Small Cell Deployment in Cellular Networks
Electronic & Electrical Engineering Data Traffic Analysis and Small Cell Deployment in Cellular Networks A THESIS SUBMITTED TO THE UNIVERSITY OF SHEFFIELD IN THE SUBJECT OF TELECOMMUNICATIONS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY. By Nan E 2016 I Abstract In this thesis, the study of small cell deployment in heterogeneous networks is presented. The research work can be divided into three aspects. The first part is user data traffic analysis for an existing 3G network in London. The second part is the deployment of additional small cells on top of existing heterogeneous networks. The third part is small cell deployment based on stochastic geometry analysis of heterogeneous networks. In the first part, an analysis of 3G network user downlink data traffic is presented. With the increasing demands for high data rate and energy-efficient cellular service, it is important to understand how cellular user data traffic changes over time and in space. A statistical model of time-varying throughput per cell and the distribution of instantaneous throughput per cell over different cells based on throughput measurements from a real-world large-scale urban cellular network are provided. The model can generate network traffic data that are very close to the measured traffic and can be used in simulations of large-scale urban-area mobile networks. In the second part of the work, three different small-cell deployment strategies are proposed. As the mobile data demand keeps growing, an existing heterogeneous network composed of macrocells and small cells may still face the problem of not being able to provide sufficient capacity for unexpected but reoccurring hot spots. -

Radio Resource Management in LTE Networks: Load Balancing in Heterogeneous Cellular Networks
Radio Resource Management in LTE Networks : Load Balancing in Heterogeneous Cellular Networks Hana Jouini To cite this version: Hana Jouini. Radio Resource Management in LTE Networks : Load Balancing in Heterogeneous Cellu- lar Networks. Networking and Internet Architecture [cs.NI]. Conservatoire national des arts et metiers - CNAM; École nationale d’ingénieurs de Tunis (Tunisie), 2017. English. NNT : 2017CNAM1153. tel-01878355 HAL Id: tel-01878355 https://tel.archives-ouvertes.fr/tel-01878355 Submitted on 21 Sep 2018 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. École doctorale Informatique, Télécommunications et Électronique (Paris), Laboratoire Centre d’Etudes et De Recherche en Informatique et Communications École doctorale Sciences et Techniques de l’Ingénieur, Systèmes de Communications, Laboratoire Systèmes de Communications THÈSE DE DOCTORAT présentée par : Hana JOUINI soutenue le : 20 décembre 2017 Pour obtenir le grade de DOCTEUR conjointement du Conservatoire National des Arts et Métiers et l’École Nationale d’Ingénieurs de Tunis Spécialité : Informatique Radio Resource Management in LTE Networks Load Balancing in Heterogeneous Cellular Networks THÈSE dirigée par M. BARKAOUI Kamel Professeur des Universités, Conservatoire National des Arts et Métiers M. EZZEDINE Tahar Professeur, École Nationale d’Ingénieurs de Tunis RAPPORTEURS M.