DOCSLIB.ORG

603: Electromagnetic Theory I

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
603: Electromagnetic Theory I 603: Electromagnetic Theory I CONTENTS Maxwell’s Equations: Introduction; units; boundary conditions. • Electrostatics: Uniqueness theorem; Green’s theorem; gauge potentials; energy • Boundary value problems in electrostatics: Method of images; separation of variables • in Cartesian, spherical polar and cylindrical polar coordinates. Dielectric media • Multipole expansion • Magnetostatics • Time-dependent fields • Contents 1 Introduction 3 1.1 Maxwell’sequations .............................. 3 1.2 Gaussianunits .................................. 4 1.3 Macroscopicmedia ................................ 6 1.4 Boundary conditions at media interfaces . ....... 8 1.5 Gaugepotentials ................................. 12 1.6 Electric field of a point charge; Coulomb’s law . ........ 14 1.7 Gauss’slaw .................................... 15 1.8 Electrostatic potential . 17 1.9 Electrostaticenergy ............................. 18 1.10Capacitance.................................... 22 2 Uniqueness Theorem, Green Functions and Method of Images 23 2.1 Uniquenesstheorem ............................... 23 2.2 Green’stheorem ................................. 27 2.3 Green functions and the boundary-value problem . ........ 28 2.4 Dirichlet and Neumann Green functions for infinite planar conductor . 32 2.5 Dirichlet Green function for spherical conductor . ........... 35 3 Separation of Variables in Cartesian Coordinates 41 3.1 Introduction.................................... 41 3.2 Separation of variables in Cartesian coordinates . ........... 42 4 Separation of variables in spherical polar coordinates 45 4.1 Series solution of the Legendre equation . ....... 47 4.2 Rodriguesformula ................................ 52 4.3 Thegeneratingfunction . 53 4.4 ExpansioninLegendrepolynomials. ..... 54 4.5 Azimuthally-symmetric solutions of Laplace’s equation............ 56 4.6 Some useful techniques for azimuthally-symmetric problems......... 59 4.7 Thesphericalharmonics . 64 4.8 General solution of Laplace’s equation without azimuthalsymmetry . 70 4.9 Another look at the generating function . ...... 72 4.10 Dirichlet Green function expansion . ....... 79 1 4.11 Inversionsymmetryrevisited . ..... 80 5 Separation of Variables in Cylindrical Polar Coordinates 82 5.1 Solutions of Bessel’s equation . ..... 84 5.2 PropertiesoftheBesselfunctions . ...... 88 5.3 A boundary-value problem in cylindrical polar coordinates.......... 92 5.4 ModifiedBesselfunctions . 93 5.5 Green function in cylindrical polar coordinates . .......... 95 6 Multipole Expansion 98 6.1 Index notation for Cartesian vectors and tensors . ......... 98 6.2 Multipole expansion in Cartesian coordinates . ......... 101 6.3 Multipole expansion using spherical harmonics . ......... 104 6.4 Another construction of the spherical harmonics . ......... 105 6.5 Multipole expansion of the energy in an external field . ......... 107 7 Dielectric Media 108 7.1 Microscopicdescription . 108 7.2 Examplesofdielectricmedia . 113 7.3 Boundary-value problems with dielectric interfaces . ............ 115 7.4 Electrostatic energy in dielectric media . ......... 123 8 Magnetostatics 126 8.1 Amp`ere’s law and the Biot-Savat law . 127 8.2 Magnetic field of a circular current loop . 131 8.3 LocalisedCurrentDistribution . 137 8.4 Force on a current distribution in an external B~ field............. 141 8.5 Magnetically permeable media . 143 8.6 Boundary conditions at medium interfaces . ....... 145 8.7 Techniques for solving boundary-value problems in magnetostatics . 145 9 Electromagnetism and Quantum Mechanics 153 9.1 The Schr¨odinger equation and gauge transformations . ........... 153 9.2 Magneticmonopoles ............................... 155 9.3 Dirac quantisation condition . 157 2 1 Introduction 1.1 Maxwell’s equations The equations now known as Maxwell’s equations were obtained over an extended period, principally during the early nineteenth century. Here, we shall take as our starting point the set of four differential equations as they were presented by Maxwell in about 1861. It was Maxwell who completed the process of constructing the equations, thereby achieving the first unification of fundamental theories in physics. Prior to Maxwell, there were two essen- tially independent theories, one describing electricity and the other describing magnetism, and it was he who brought about the synthesis that unified them into a single theory of electromagnetism. It was only later, after Einstein developed the theory of Special Relativity in 1905, that the magnitude of Maxwell’s achievement really became clear. Especially, a quite remarkable feature of Maxwell’s 1861 equations is that they are already completely compatible with special relativity, with no need for modification of any kind.1 Aside from changes in notation and units, Maxwell’s equations have remained otherwise unaltered since 1861. Let us begin by considering Maxwell’s equations in free space, by which is meant that the space outside of any conducting surfaces is assumed to be a vacuum. Using the SI system of units, Maxwell’s equations are: ′ ~ ′ ′ ρ ′ ∂E ′ ~ E~ = , ~ B~ µ0ǫ0 = µ0J~ , ∇ · ǫ0 ∇× − ∂t ∂B~ ′ ~ B~ ′ = 0 , ~ E~ ′ + = 0 . (1.1) ∇ · ∇× ∂t Observe that I have written these equations with a “prime” on the electric field E~ the magnetic field B~ , the electric charge density ρ and the electric current density J~ . This is to indicate that these quantities are all expressed in the SI system of units. (The SI system typically maximises the number of “redundant” dimensionful constants, and so one might say that it is Super Inconvenient.) The remaining quantities appearing in (1.1) are the constants ǫ0 and µ0, which are, respectively, the permitivity of free space and the permeability of free space. They have the values ǫ 8.85419 10−12 Farads/metre , µ = 4π 10−7 Henries/metre (1.2) 0 ≈ × 0 × 1This contrasts with the case of Newtonian mechanics, which is not compatible with special relativity and therefore did not survive as a “fundamental” theory after 1905. 3 1.2 Gaussian units SI units have their virtues for some purposes, but they can also be quite inconvenient in practice. This seems to be especially true in electromagnetism, and for this reason it is often more convenient to stick with an earlier system, known as Gaussian units. In this system, Maxwell’s equations in free space take the form 1 ∂E~ 4π ~ E~ = 4πρ , ~ B~ = J~ , ∇ · ∇× − c ∂t c 1 ∂B~ ~ B~ = 0 , ~ E~ + = 0 , (1.3) ∇ · ∇× c ∂t where c is the speed of light. Observe that here, we are writing the equations using the unprimed quantities E~ , B~ , ρ and J~ , and it will probably therefore come as no surprise that it is this Gaussian system of units that I prefer to use. It should already be evident upon comparing (1.1) and (1.3) that Gaussian system is somewhat simpler, in that one needs only one “fundamental constant” (i.e. the speed of light) rather than two (the permittivity and the permeability of free space).2 The introduction of the 4π factors in (1.3) may perhaps seem tiresome, but the advantage of doing so will become apparent in due course. (There can be no escape from having 4π factors somewhere, because of the fact that a unit sphere has area 4π.) In order to ensure that we can, whenever desired, revert to SI units, it is useful to work out explicitly the relation between the Gaussian quantities (denoted without primes, as in (1.3)) and the SI quantities (denoted with primes, as in (1.1)). In order to do this, we first need to understand a very important property of the Maxwell equations, namely that they imply the existence of electromagnetic waves that propagate at the speed of light. Consider the Maxwell equations (1.1) in a completely empty region of space, where there ′ is no charge density ρ′ and no current density J~ . Taking the curl of the last equation, and using the vector identity ~ (~ V~ )= ~ (~ V~ ) 2V~ , we obtain ∇× ∇× ∇ ∇ · −∇ ∂ 2E~ ′ + ~ (~ E~ ′)+ ~ B~ ′ = 0 , (1.4) −∇ ∇ ∇ · ∂t∇× and hence, since the partial derivative ∂/∂t commutes with the spatial partial derivatives 2Actually, one can do even better by changing the units in which one measures length from the metre to the light second, or alternatively, changing the unit of time to the light metre (the time light takes to travel 1 metre). In either of these systems of units, the speed of light becomes equal to 1. 4 in ~ , ∇ ∂B~ ′ 2E~ ′ + ~ (~ E~ ′)+ ~ = 0 . (1.5) −∇ ∇ ∇ · ∇× ∂t ′ Using the first equation in (1.1) (with ρ′ = 0) and the second equation (with J~ = 0) then gives ∂2 2E~ ′ µ ǫ E~ ′ = 0 . (1.6) ∇ − 0 0 ∂t2 Analogous manipulations show that B~ ′ satisfies an identical equation. We see, therefore, that the electric and magnetic fields satisfy an equation for waves that propagate at the speed 1 c = 2.99792 108 metres/second . (1.7) √µ0ǫ0 ≈ × This is precisely the speed of light in vacuo, and these wave solutions describe the propa- gation of radio waves, light, etc. With this preliminary, we are nearly ready to establish the relation between the SI units used in (1.1), and the Gaussian units used in (1.3). The procedure for doing this is to introduce constant factors α, β, γ and δ that relate the primed to the unprimed quantities, ′ E~ ′ = αE~ , B~ ′ = βB~ , ρ′ = γρ , J~ = δJ~ , (1.8) and to fix the values of these constants by demanding that plugging (1.8) into (1.1) should give (1.3). It is essential, in doing so, that we have the relation (1.7) between c, µ0 and ǫ0. Elementary algebra then gives γ γ µ α = , β = 0 , δ = γ . (1.9) 4πǫ 4π ǫ 0 r 0 Observe that the value of the constant γ has not yet been determined. This means that we can choose any value for γ, and we may use this freedom in order to make some other equation as nice as possible by removing superfluous constant factors. Consider Coulomb’s law, giving the force between two electric charges separated by a distance R. We again need ′ ′ to distinguish between the charges q1 and q2 expressed in SI units, and the charges q1 and ′ q2 expressed in Gaussian units. Since we have the relation ρ = γρ between charge densities in the two systems, and since the unit of volume is the same in the two systems, it follows that the charges will also be related by the same factor of γ: q′ = γq .
Load more

Recommended publications
  • Mathematics 412 Partial Differential Equations
    Mathematics 412 Partial Differential Equations c S. A. Fulling Fall, 2005 The Wave Equation This introductory example will have three parts.* 1. I will show how a particular, simple partial differential equation (PDE) arises in a physical problem. 2. We’ll look at its solutions, which happen to be unusually easy to find in this case. 3. We’ll solve the equation again by separation of variables, the central theme of this course, and see how Fourier series arise. The wave equation in two variables (one space, one time) is ∂2u ∂2u = c2 , ∂t2 ∂x2 where c is a constant, which turns out to be the speed of the waves described by the equation. Most textbooks derive the wave equation for a vibrating string (e.g., Haber- man, Chap. 4). It arises in many other contexts — for example, light waves (the electromagnetic field). For variety, I shall look at the case of sound waves (motion in a gas). Sound waves Reference: Feynman Lectures in Physics, Vol. 1, Chap. 47. We assume that the gas moves back and forth in one dimension only (the x direction). If there is no sound, then each bit of gas is at rest at some place (x,y,z). There is a uniform equilibrium density ρ0 (mass per unit volume) and pressure P0 (force per unit area). Now suppose the gas moves; all gas in the layer at x moves the same distance, X(x), but gas in other layers move by different distances. More precisely, at each time t the layer originally at x is displaced to x + X(x,t).
    [Show full text]
  • Electrostatics Vs Magnetostatics Electrostatics Magnetostatics
    Electrostatics vs Magnetostatics Electrostatics Magnetostatics Stationary charges ⇒ Constant Electric Field Steady currents ⇒ Constant Magnetic Field Coulomb’s Law Biot-Savart’s Law 1 ̂ ̂ 4 4 (Inverse Square Law) (Inverse Square Law) Electric field is the negative gradient of the Magnetic field is the curl of magnetic vector electric scalar potential. potential. 1 ′ ′ ′ ′ 4 |′| 4 |′| Electric Scalar Potential Magnetic Vector Potential Three Poisson’s equations for solving Poisson’s equation for solving electric scalar magnetic vector potential potential. Discrete 2 Physical Dipole ′′′ Continuous Magnetic Dipole Moment Electric Dipole Moment 1 1 1 3 ∙̂̂ 3 ∙̂̂ 4 4 Electric field cause by an electric dipole Magnetic field cause by a magnetic dipole Torque on an electric dipole Torque on a magnetic dipole ∙ ∙ Electric force on an electric dipole Magnetic force on a magnetic dipole ∙ ∙ Electric Potential Energy Magnetic Potential Energy of an electric dipole of a magnetic dipole Electric Dipole Moment per unit volume Magnetic Dipole Moment per unit volume (Polarisation) (Magnetisation) ∙ Volume Bound Charge Density Volume Bound Current Density ∙ Surface Bound Charge Density Surface Bound Current Density Volume Charge Density Volume Current Density Net , Free , Bound Net , Free , Bound Volume Charge Volume Current Net , Free , Bound Net ,Free , Bound 1 = Electric field = Magnetic field = Electric Displacement = Auxiliary
    [Show full text]
  • Review of Electrostatics and Magenetostatics
    Review of electrostatics and magenetostatics January 12, 2016 1 Electrostatics 1.1 Coulomb’s law and the electric field Starting from Coulomb’s law for the force produced by a charge Q at the origin on a charge q at x, qQ F (x) = 2 x^ 4π0 jxj where x^ is a unit vector pointing from Q toward q. We may generalize this to let the source charge Q be at an arbitrary postion x0 by writing the distance between the charges as jx − x0j and the unit vector from Qto q as x − x0 jx − x0j Then Coulomb’s law becomes qQ x − x0 x − x0 F (x) = 2 0 4π0 jx − xij jx − x j Define the electric field as the force per unit charge at any given position, F (x) E (x) ≡ q Q x − x0 = 3 4π0 jx − x0j We think of the electric field as existing at each point in space, so that any charge q placed at x experiences a force qE (x). Since Coulomb’s law is linear in the charges, the electric field for multiple charges is just the sum of the fields from each, n X qi x − xi E (x) = 4π 3 i=1 0 jx − xij Knowing the electric field is equivalent to knowing Coulomb’s law. To formulate the equivalent of Coulomb’s law for a continuous distribution of charge, we introduce the charge density, ρ (x). We can define this as the total charge per unit volume for a volume centered at the position x, in the limit as the volume becomes “small”.
    [Show full text]
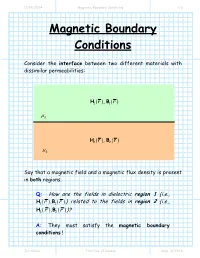
  • Magnetic Boundary Conditions 1/6
    11/28/2004 Magnetic Boundary Conditions 1/6 Magnetic Boundary Conditions Consider the interface between two different materials with dissimilar permeabilities: HB11(r,) (r) µ1 HB22(r,) (r) µ2 Say that a magnetic field and a magnetic flux density is present in both regions. Q: How are the fields in dielectric region 1 (i.e., HB11()rr, ()) related to the fields in region 2 (i.e., HB22()rr, ())? A: They must satisfy the magnetic boundary conditions ! Jim Stiles The Univ. of Kansas Dept. of EECS 11/28/2004 Magnetic Boundary Conditions 2/6 First, let’s write the fields at the interface in terms of their normal (e.g.,Hn ()r ) and tangential (e.g.,Ht (r ) ) vector components: H r = H r + H r H1n ()r 1 ( ) 1t ( ) 1n () ˆan µ 1 H1t (r ) H2t (r ) H2n ()r H2 (r ) = H2t (r ) + H2n ()r µ 2 Our first boundary condition states that the tangential component of the magnetic field is continuous across a boundary. In other words: HH12tb(rr) = tb( ) where rb denotes to any point along the interface (e.g., material boundary). Jim Stiles The Univ. of Kansas Dept. of EECS 11/28/2004 Magnetic Boundary Conditions 3/6 The tangential component of the magnetic field on one side of the material boundary is equal to the tangential component on the other side ! We can likewise consider the magnetic flux densities on the material interface in terms of their normal and tangential components: BHrr= µ B1n ()r 111( ) ( ) ˆan µ 1 B1t (r ) B2t (r ) B2n ()r BH222(rr) = µ ( ) µ2 The second magnetic boundary condition states that the normal vector component of the magnetic flux density is continuous across the material boundary.
    [Show full text]
  • Chapter 2. Steady States and Boundary Value Problems
    “rjlfdm” 2007/4/10 i i page 13 i i Copyright ©2007 by the Society for Industrial and Applied Mathematics This electronic version is for personal use and may not be duplicated or distributed. Chapter 2 Steady States and Boundary Value Problems We will first consider ordinary differential equations (ODEs) that are posed on some in- terval a < x < b, together with some boundary conditions at each end of the interval. In the next chapter we will extend this to more than one space dimension and will study elliptic partial differential equations (ODEs) that are posed in some region of the plane or Q5 three-dimensional space and are solved subject to some boundary conditions specifying the solution and/or its derivatives around the boundary of the region. The problems considered in these two chapters are generally steady-state problems in which the solution varies only with the spatial coordinates but not with time. (But see Section 2.16 for a case where Œa; b is a time interval rather than an interval in space.) Steady-state problems are often associated with some time-dependent problem that describes the dynamic behavior, and the 2-point boundary value problem (BVP) or elliptic equation results from considering the special case where the solution is steady in time, and hence the time-derivative terms are equal to zero, simplifying the equations. 2.1 The heat equation As a specific example, consider the flow of heat in a rod made out of some heat-conducting material, subject to some external heat source along its length and some boundary condi- tions at each end.
    [Show full text]
  • Solving the Boundary Value Problems for Differential Equations with Fractional Derivatives by the Method of Separation of Variables
    mathematics Article Solving the Boundary Value Problems for Differential Equations with Fractional Derivatives by the Method of Separation of Variables Temirkhan Aleroev National Research Moscow State University of Civil Engineering (NRU MGSU), Yaroslavskoe Shosse, 26, 129337 Moscow, Russia; [email protected] Received: 16 September 2020; Accepted: 22 October 2020; Published: 29 October 2020 Abstract: This paper is devoted to solving boundary value problems for differential equations with fractional derivatives by the Fourier method. The necessary information is given (in particular, theorems on the completeness of the eigenfunctions and associated functions, multiplicity of eigenvalues, and questions of the localization of root functions and eigenvalues are discussed) from the spectral theory of non-self-adjoint operators generated by differential equations with fractional derivatives and boundary conditions of the Sturm–Liouville type, obtained by the author during implementation of the method of separation of variables (Fourier). Solutions of boundary value problems for a fractional diffusion equation and wave equation with a fractional derivative are presented with respect to a spatial variable. Keywords: eigenvalue; eigenfunction; function of Mittag–Leffler; fractional derivative; Fourier method; method of separation of variables In memoriam of my Father Sultan and my son Bibulat 1. Introduction Let j(x) L (0, 1). Then the function 2 1 x a d− 1 a 1 a j(x) (x t) − j(t) dt L1(0, 1) dx− ≡ G(a) − 2 Z0 is known as a fractional integral of order a > 0 beginning at x = 0 [1]. Here G(a) is the Euler gamma-function. As is known (see [1]), the function y(x) L (0, 1) is called the fractional derivative 2 1 of the function j(x) L (0, 1) of order a > 0 beginning at x = 0, if 2 1 a d− j(x) = a y(x), dx− which is written da y(x) = j(x).
    [Show full text]
  • Topics on Calculus of Variations
    TOPICS ON CALCULUS OF VARIATIONS AUGUSTO C. PONCE ABSTRACT. Lecture notes presented in the School on Nonlinear Differential Equa- tions (October 9–27, 2006) at ICTP, Trieste, Italy. CONTENTS 1. The Laplace equation 1 1.1. The Dirichlet Principle 2 1.2. The dawn of the Direct Methods 4 1.3. The modern formulation of the Calculus of Variations 4 1 1.4. The space H0 (Ω) 4 1.5. The weak formulation of (1.2) 8 1.6. Weyl’s lemma 9 2. The Poisson equation 11 2.1. The Newtonian potential 11 2.2. Solving (2.1) 12 3. The eigenvalue problem 13 3.1. Existence step 13 3.2. Regularity step 15 3.3. Proof of Theorem 3.1 16 4. Semilinear elliptic equations 16 4.1. Existence step 17 4.2. Regularity step 18 4.3. Proof of Theorem 4.1 20 References 20 1. THE LAPLACE EQUATION Let Ω ⊂ RN be a body made of some uniform material; on the boundary of Ω, we prescribe some fixed temperature f. Consider the following Question. What is the equilibrium temperature inside Ω? Date: August 29, 2008. 1 2 AUGUSTO C. PONCE Mathematically, if u denotes the temperature in Ω, then we want to solve the equation ∆u = 0 in Ω, (1.1) u = f on ∂Ω. We shall always assume that f : ∂Ω → R is a given smooth function and Ω ⊂ RN , N ≥ 3, is a smooth, bounded, connected open set. We say that u is a classical solution of (1.1) if u ∈ C2(Ω) and u satisfies (1.1) at every point of Ω.
    [Show full text]
  • THE IMPACT of RIEMANN's MAPPING THEOREM in the World
    THE IMPACT OF RIEMANN'S MAPPING THEOREM GRANT OWEN In the world of mathematics, scholars and academics have long sought to understand the work of Bernhard Riemann. Born in a humble Ger- man home, Riemann became one of the great mathematical minds of the 19th century. Evidence of his genius is reflected in the greater mathematical community by their naming 72 different mathematical terms after him. His contributions range from mathematical topics such as trigonometric series, birational geometry of algebraic curves, and differential equations to fields in physics and philosophy [3]. One of his contributions to mathematics, the Riemann Mapping Theorem, is among his most famous and widely studied theorems. This theorem played a role in the advancement of several other topics, including Rie- mann surfaces, topology, and geometry. As a result of its widespread application, it is worth studying not only the theorem itself, but how Riemann derived it and its impact on the work of mathematicians since its publication in 1851 [3]. Before we begin to discover how he derived his famous mapping the- orem, it is important to understand how Riemann's upbringing and education prepared him to make such a contribution in the world of mathematics. Prior to enrolling in university, Riemann was educated at home by his father and a tutor before enrolling in high school. While in school, Riemann did well in all subjects, which strengthened his knowl- edge of philosophy later in life, but was exceptional in mathematics. He enrolled at the University of G¨ottingen,where he learned from some of the best mathematicians in the world at that time.
    [Show full text]
  • Magnetostatics: Part 1 We Present Magnetostatics in Comparison with Electrostatics
    Magnetostatics: Part 1 We present magnetostatics in comparison with electrostatics. Sources of the fields: Electric field E: Coulomb’s law Magnetic field B: Biot-Savart law Forces exerted by the fields: Electric: F = qE Mind the notations, both Magnetic: F = qvB printed and hand‐written Does the magnetic force do any work to the charge? F B, F v Positive charge moving at v B Negative charge moving at v B Steady state: E = vB By measuring the polarity of the induced voltage, we can determine the sign of the moving charge. If the moving charge carriers is in a perfect conductor, then we can have an electric field inside the perfect conductor. Does this contradict what we have learned in electrostatics? Notice that the direction of the magnetic force is the same for both positive and negative charge carriers. Magnetic force on a current carrying wire The magnetic force is in the same direction regardless of the charge carrier sign. If the charge carrier is negative Carrier density Charge of each carrier For a small piece of the wire dl scalar Notice that v // dl A current-carrying wire in an external magnetic field feels the force exerted by the field. If the wire is not fixed, it will be moved by the magnetic force. Some work must be done. Does this contradict what we just said? For a wire from point A to point B, For a wire loop, If B is a constant all along the loop, because Let’s look at a rectangular wire loop in a uniform magnetic field B.
    [Show full text]
  • Modeling of Ferrofluid Passive Cooling System
    Excerpt from the Proceedings of the COMSOL Conference 2010 Boston Modeling of Ferrofluid Passive Cooling System Mengfei Yang*,1,2, Robert O’Handley2 and Zhao Fang2,3 1M.I.T., 2Ferro Solutions, Inc, 3Penn. State Univ. *500 Memorial Dr, Cambridge, MA 02139, [email protected] Abstract: The simplicity of a ferrofluid-based was to develop a model that supports results passive cooling system makes it an appealing from experiments conducted on a cylindrical option for devices with limited space or other container of ferrofluid with a heat source and physical constraints. The cooling system sink [Figure 1]. consists of a permanent magnet and a ferrofluid. The experiments involved changing the Ferrofluids are composed of nanoscale volume of the ferrofluid and moving the magnet ferromagnetic particles with a temperature- to different positions outside the ferrofluid dependant magnetization suspended in a liquid container. These experiments tested 1) the effect solvent. The cool, magnetic ferrofluid near the of bringing the heat source and heat sink closer heat sink is attracted toward a magnet positioned together and using less ferrofluid, and 2) the near the heat source, thereby displacing the hot, optimal position for the permanent magnet paramagnetic ferrofluid near the heat source and between the heat source and sink. In the model, setting up convective cooling. This paper temperature-dependent magnetic properties were explores how COMSOL Multiphysics can be incorporated into the force component of the used to model a simple cylinder representation of momentum equation, which was coupled to the such a cooling system. Numerical results from heat transfer module. The model was compared the model displayed the same trends as empirical with experimental results for steady-state data from experiments conducted on the cylinder temperature trends and for appropriate velocity cooling system.
    [Show full text]
  • FETI-DP Domain Decomposition Method
    ECOLE´ POLYTECHNIQUE FED´ ERALE´ DE LAUSANNE Master Project FETI-DP Domain Decomposition Method Supervisors: Author: Davide Forti Christoph Jaggli¨ Dr. Simone Deparis Prof. Alfio Quarteroni A thesis submitted in fulfilment of the requirements for the degree of Master in Mathematical Engineering in the Chair of Modelling and Scientific Computing Mathematics Section June 2014 Declaration of Authorship I, Christoph Jaggli¨ , declare that this thesis titled, 'FETI-DP Domain Decomposition Method' and the work presented in it are my own. I confirm that: This work was done wholly or mainly while in candidature for a research degree at this University. Where any part of this thesis has previously been submitted for a degree or any other qualification at this University or any other institution, this has been clearly stated. Where I have consulted the published work of others, this is always clearly at- tributed. Where I have quoted from the work of others, the source is always given. With the exception of such quotations, this thesis is entirely my own work. I have acknowledged all main sources of help. Where the thesis is based on work done by myself jointly with others, I have made clear exactly what was done by others and what I have contributed myself. Signed: Date: ii ECOLE´ POLYTECHNIQUE FED´ ERALE´ DE LAUSANNE Abstract School of Basic Science Mathematics Section Master in Mathematical Engineering FETI-DP Domain Decomposition Method by Christoph Jaggli¨ FETI-DP is a dual iterative, nonoverlapping domain decomposition method. By a Schur complement procedure, the solution of a boundary value problem is reduced to solving a symmetric and positive definite dual problem in which the variables are directly related to the continuity of the solution across the interface between the subdomains.
    [Show full text]
  • An Improved Riemann Mapping Theorem and Complexity In
    AN IMPROVED RIEMANN MAPPING THEOREM AND COMPLEXITY IN POTENTIAL THEORY STEVEN R. BELL Abstract. We discuss applications of an improvement on the Riemann map- ping theorem which replaces the unit disc by another “double quadrature do- main,” i.e., a domain that is a quadrature domain with respect to both area and boundary arc length measure. Unlike the classic Riemann Mapping Theo- rem, the improved theorem allows the original domain to be finitely connected, and if the original domain has nice boundary, the biholomorphic map can be taken to be close to the identity, and consequently, the double quadrature do- main close to the original domain. We explore some of the parallels between this new theorem and the classic theorem, and some of the similarities between the unit disc and the double quadrature domains that arise here. The new results shed light on the complexity of many of the objects of potential theory in multiply connected domains. 1. Introduction The unit disc is the most famous example of a “double quadrature domain.” The average of an analytic function on the disc with respect to both area measure and with respect to boundary arc length measure yield the value of the function at the origin when these averages make sense. The Riemann Mapping Theorem states that when Ω is a simply connected domain in the plane that is not equal to the whole complex plane, a biholomorphic map of Ω to this famous double quadrature domain exists. We proved a variant of the Riemann Mapping Theorem in [16] that allows the domain Ω = C to be simply or finitely connected.
    [Show full text]