DOCSLIB.ORG

Angle Relationships in Circles 10.5

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Angle Relationships in Circles 10.5 10.5 Angle Relationships in Circles EEssentialssential QQuestionuestion When a chord intersects a tangent line or another chord, what relationships exist among the angles and arcs formed? Angles Formed by a Chord and Tangent Line Work with a partner. Use dynamic geometry software. a. Construct a chord in a circle. At Sample one of the endpoints of the chord, construct a tangent line to the circle. b. Find the measures of the two angles C B formed by the chord and the tangent line. c. Find the measures of the two A circular arcs determined by the chord. d. Repeat parts (a)–(c) several times. D Record your results in a table. Then write a conjecture that summarizes the data. Angles Formed by Intersecting Chords Work with a partner. Use dynamic geometry software. a. Construct two chords that Sample intersect inside a circle. b. Find the measure of one D CONSTRUCTING of the angles formed by the B VIABLE ARGUMENTS intersecting chords. To be profi cient in math, c. Find the measures of the arcs C you need to understand intercepted by the angle in part (b) A and use stated assumptions, and its vertical angle. What do defi nitions, and previously you observe? E established results. d. Repeat parts (a)–(c) several times. Record your results in a table. Then write a conjecture that summarizes the data. CCommunicateommunicate YourYour AnswerAnswer 3. When a chord intersects a tangent line or another chord, what relationships exist 148° among the angles and arcs formed? m m ∠ 1 4. Line is tangent to the circle in the fi gure at the left. Find the measure of 1. 5. Two chords intersect inside a circle to form a pair of vertical angles with measures of 55°. Find the sum of the measures of the arcs intercepted by the two angles. Section 10.5 Angle Relationships in Circles 561 hhs_geo_pe_1005.indds_geo_pe_1005.indd 561561 11/19/15/19/15 22:37:37 PMPM 10.5 Lesson WWhathat YYouou WWillill LLearnearn Find angle and arc measures. Core VocabularyVocabulary Use circumscribed angles. circumscribed angle, p. 564 Finding Angle and Arc Measures Previous tangent TTheoremheorem chord secant Theorem 10.14 Tangent and Intersected Chord Theorem If a tangent and a chord intersect at a point on a circle, B then the measure of each angle formed is one-half the C measure of its intercepted arc. 2 1 A m∠1 = 1 mAB m∠2 = 1 mBCA Proof Ex. 33, p. 568 2 2 Finding Angle and Arc Measures Line m is tangent to the circle. Find the measure of the red angle or arc. a. A b. K m 130° 125° L 1 J B m SOLUTION 1 ២ m∠ = — ° = ° m KJL = ° = ° a. 1 2 (130 ) 65 b. 2(125 ) 250 MMonitoringonitoring PProgressrogress Help in English and Spanish at BigIdeasMath.com Line m is tangent to the circle. Find the indicated measure. ២ ២ 1. m∠1 2. m RST 3. m XY m m S m 1 ° Y 80° T 98 X 210° R CCoreore CConceptoncept Intersecting Lines and Circles If two nonparallel lines intersect a circle, there are three places where the lines can intersect. on the circle inside the circle outside the circle 562 Chapter 10 Circles hhs_geo_pe_1005.indds_geo_pe_1005.indd 562562 11/19/15/19/15 22:37:37 PMPM TTheoremsheorems Theorem 10.15 Angles Inside the Circle Theorem D If two chords intersect inside a circle, then the measure of A sum 1 each angle is one-half the of the measures of the arcs 2 C intercepted by the angle and its vertical angle. B m∠1 = 1 (mDC + mAB ), 2 Proof Ex. 35, p. 568 m∠2 = 1 (mAD + mBC ) 2 Theorem 10.16 Angles Outside the Circle Theorem If a tangent and a secant, two tangents, or two secants intersect outside a circle, then the measure of the angle formed is one-half the difference of the measures of the intercepted arcs. B P X Q A W 1 2 3 Z C R Y m∠1 = 1 (mBC − mAC ) m∠2 = 1 (mPQR − mPR ) m∠3 = 1 (mXY − mWZ ) 2 2 2 Proof Ex. 37, p. 568 Finding an Angle Measure Find the value of x. a. ° b. C D 130 M ° x° B 76 J L x° 178° K A 156° SOLUTION — — a. The chords JL and KM intersect b. The tangent CD៮៮៮⃗ and the secant CB៮៮៮⃗ inside the circle. Use the Angles intersect outside the circle. Use the Inside the Circle Theorem. Angles Outside the Circle Theorem. 1 ២ ២ 1 ២ ២ x° = — m JM + m LK m∠BCD = — m AD − m BD 2 ( ) 2 ( ) 1 1 x° = — ° + x° = — ° − 2 ( 130 156°) 2 ( 178 76°) x = 143 x = 51 So, the value of x is 143. So, the value of x is 51. MMonitoringonitoring PProgressrogress Help in English and Spanish at BigIdeasMath.com Find the value of the variable. 4. y° 5. F A B a° 102° K 44° C G D J H 95° 30° Section 10.5 Angle Relationships in Circles 563 hhs_geo_pe_1005.indds_geo_pe_1005.indd 563563 11/19/15/19/15 22:37:37 PMPM Using Circumscribed Angles CCoreore CConceptoncept Circumscribed Angle A A circumscribed angle is an angle B whose sides are tangent to a circle. circumscribed C angle TTheoremheorem Theorem 10.17 Circumscribed Angle Theorem A The measure of a circumscribed angle is equal to 180° minus the measure of the central angle that intercepts D C the same arc. B Proof Ex. 38, p. 568 m∠ADB = 180° − m∠ACB Finding Angle Measures Find the value of x. a. D b. E A J x° x° ° G 135 ° C H 30 B F SOLUTION a. Use the Circumscribed Angle Theorem to fi nd m∠ADB. m∠ADB = 180° − m∠ACB Circumscribed Angle Theorem x° = 180° − 135° Substitute. x = 45 Subtract. So, the value of x is 45. b. Use the Measure of an Inscribed Angle Theorem (Theorem 10.10) and the Circumscribed Angle Theorem to fi nd m∠EJF. 1 ២ m∠EJF = — m EF 2 Measure of an Inscribed Angle Theorem 1 m∠EJF = — m∠EGF 2 Defi nition of minor arc 1 m∠EJF = — ° − m∠EHF 2 (180 ) Circumscribed Angle Theorem 1 m∠EJF = — ° − ° 2 (180 30 ) Substitute. 1 x = — − 2 (180 30) Substitute. x = 75 Simplify. So, the value of x is 75. 564 Chapter 10 Circles hhs_geo_pe_1005.indds_geo_pe_1005.indd 564564 11/19/15/19/15 22:37:37 PMPM Modeling with Mathematics The northern lights are bright fl ashes of colored C light between 50 and 200 miles above Earth. A BD fl ash occurs 150 miles ២above Earth at point C. What is the measure of BD , the portion of Earth from which the fl ash is visible? (Earth’s radius 4150 mi 4000 mi is approximately 4000 miles.) A E SOLUTION Not drawn to scale 1. Understand the Problem You are given the approximate radius of Earth and the distance above Earth that the fl ash occurs. You need to fi nd the measure of the arc that represents the portion of Earth from which the fl ash is visible. 2. Make a Plan Use properties of tangents, triangle congruence, and angles outside a circle to fi nd the arc measure. — — — — — — 3. Solve the Problem Because CB and CD are tangents, CB ⊥ AB and CD ⊥ AD BC— ≅ DC— by the Tangent Line to Circle Theorem (Theorem 10.1). Also, — — by the External Tangent Congruence Theorem (Theorem 10.2), and CA ≅ CA by the Refl exive Property of Congruence (Theorem 2.1). So, △ABC ≅ △ADC by the Hypotenuse-Leg Congruence Theorem (Theorem 5.9). Because corresponding COMMON ERROR parts of congruent triangles are congruent, ∠BCA ≅ ∠DCA. Solve right △CBA to fi nd that m∠BCA ≈ 74.5°. So, m∠BCD ≈ 2(74.5°) = 149°. Because the value for m∠BCD is an m∠BCD = 180° − m∠BAD Circumscribed Angle Theorem ២ approximation, use the m∠BCD = 180° − m BD Defi nition of minor arc symbol ≈ instead of =. ២ 149° ≈ 180° − m BD Substitute. ២ ២ 31° ≈ m BD Solve for m BD . The measure of the arc from which the fl ash is visible is about 31°. 4. Look Back You can use inverse trigonometric ratios to fi nd m∠BAC and m∠DAC. m∠BAC = cos−1 —4000 ≈ 15.5° ( 4150) 4000 m∠DAC = cos−1 — ≈ 15.5° ( 4150) ២ So, m∠BAD ≈ 15.5° + 15.5° = 31°, and therefore m BD ≈ 31°. Monitoring Progress Help in English and Spanish at BigIdeasMath.com Find the value of x. 6. 7. T K x° P B R N x° 120° M CD Q L 50° 4002.73 mi S A 4000 mi 8. You are on top of Mount២ Rainier on a clear day. You are about 2.73 miles above sea level at point B. Find m CD , which represents the part of Earth that you can see. Not drawn to scale Section 10.5 Angle Relationships in Circles 565 hs_geo_pe_1005.indd 565 3/9/16 9:31 AM 10.5 Exercises Dynamic Solutions available at BigIdeasMath.com VVocabularyocabulary andand CoreCore ConceptConcept CheckCheck ⃖៮៮⃗ ⃖៮៮⃗ 1. COMPLETE THE SENTENCE Points A, B, C, and D are on a circle, and AB intersects CD at point P. 1 ២ ២ m∠APC = — m BD − m AC P If 2 ( ), then point is ______ the circle. 2. WRITING Explain how to fi nd the measure of a circumscribed angle. MMonitoringonitoring ProgressProgress andand ModelingModeling withwith MathematicsMathematics In Exercises 3–6, line t is tangent to the circle.
Load more

Recommended publications
  • Infinitesimal and Tangent to Polylogarithmic Complexes For
    AIMS Mathematics, 4(4): 1248–1257. DOI:10.3934/math.2019.4.1248 Received: 11 June 2019 Accepted: 11 August 2019 http://www.aimspress.com/journal/Math Published: 02 September 2019 Research article Infinitesimal and tangent to polylogarithmic complexes for higher weight Raziuddin Siddiqui* Department of Mathematical Sciences, Institute of Business Administration, Karachi, Pakistan * Correspondence: Email: [email protected]; Tel: +92-213-810-4700 Abstract: Motivic and polylogarithmic complexes have deep connections with K-theory. This article gives morphisms (different from Goncharov’s generalized maps) between |-vector spaces of Cathelineau’s infinitesimal complex for weight n. Our morphisms guarantee that the sequence of infinitesimal polylogs is a complex. We are also introducing a variant of Cathelineau’s complex with the derivation map for higher weight n and suggesting the definition of tangent group TBn(|). These tangent groups develop the tangent to Goncharov’s complex for weight n. Keywords: polylogarithm; infinitesimal complex; five term relation; tangent complex Mathematics Subject Classification: 11G55, 19D, 18G 1. Introduction The classical polylogarithms represented by Lin are one valued functions on a complex plane (see [11]). They are called generalization of natural logarithms, which can be represented by an infinite series (power series): X1 zk Li (z) = = − ln(1 − z) 1 k k=1 X1 zk Li (z) = 2 k2 k=1 : : X1 zk Li (z) = for z 2 ¼; jzj < 1 n kn k=1 The other versions of polylogarithms are Infinitesimal (see [8]) and Tangential (see [9]). We will discuss group theoretic form of infinitesimal and tangential polylogarithms in x 2.3, 2.4 and 2.5 below.
    [Show full text]
  • Lesson 3: Rectangles Inscribed in Circles
    NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 3 M5 GEOMETRY Lesson 3: Rectangles Inscribed in Circles Student Outcomes . Inscribe a rectangle in a circle. Understand the symmetries of inscribed rectangles across a diameter. Lesson Notes Have students use a compass and straightedge to locate the center of the circle provided. If necessary, remind students of their work in Module 1 on constructing a perpendicular to a segment and of their work in Lesson 1 in this module on Thales’ theorem. Standards addressed with this lesson are G-C.A.2 and G-C.A.3. Students should be made aware that figures are not drawn to scale. Classwork Scaffolding: Opening Exercise (9 minutes) Display steps to construct a perpendicular line at a point. Students follow the steps provided and use a compass and straightedge to find the center of a circle. This exercise reminds students about constructions previously . Draw a segment through the studied that are needed in this lesson and later in this module. point, and, using a compass, mark a point equidistant on Opening Exercise each side of the point. Using only a compass and straightedge, find the location of the center of the circle below. Label the endpoints of the Follow the steps provided. segment 퐴 and 퐵. Draw chord 푨푩̅̅̅̅. Draw circle 퐴 with center 퐴 . Construct a chord perpendicular to 푨푩̅̅̅̅ at and radius ̅퐴퐵̅̅̅. endpoint 푩. Draw circle 퐵 with center 퐵 . Mark the point of intersection of the perpendicular chord and the circle as point and radius ̅퐵퐴̅̅̅. 푪. Label the points of intersection .
    [Show full text]
  • Squaring the Circle a Case Study in the History of Mathematics the Problem
    Squaring the Circle A Case Study in the History of Mathematics The Problem Using only a compass and straightedge, construct for any given circle, a square with the same area as the circle. The general problem of constructing a square with the same area as a given figure is known as the Quadrature of that figure. So, we seek a quadrature of the circle. The Answer It has been known since 1822 that the quadrature of a circle with straightedge and compass is impossible. Notes: First of all we are not saying that a square of equal area does not exist. If the circle has area A, then a square with side √A clearly has the same area. Secondly, we are not saying that a quadrature of a circle is impossible, since it is possible, but not under the restriction of using only a straightedge and compass. Precursors It has been written, in many places, that the quadrature problem appears in one of the earliest extant mathematical sources, the Rhind Papyrus (~ 1650 B.C.). This is not really an accurate statement. If one means by the “quadrature of the circle” simply a quadrature by any means, then one is just asking for the determination of the area of a circle. This problem does appear in the Rhind Papyrus, but I consider it as just a precursor to the construction problem we are examining. The Rhind Papyrus The papyrus was found in Thebes (Luxor) in the ruins of a small building near the Ramesseum.1 It was purchased in 1858 in Egypt by the Scottish Egyptologist A.
    [Show full text]
  • 2. the Tangent Line
    2. The Tangent Line The tangent line to a circle at a point P on its circumference is the line perpendicular to the radius of the circle at P. In Figure 1, The line T is the tangent line which is Tangent Line perpendicular to the radius of the circle at the point P. T Figure 1: A Tangent Line to a Circle While the tangent line to a circle has the property that it is perpendicular to the radius at the point of tangency, it is not this property which generalizes to other curves. We shall make an observation about the tangent line to the circle which is carried over to other curves, and may be used as its defining property. Let us look at a specific example. Let the equation of the circle in Figure 1 be x22 + y = 25. We may easily determine the equation of the tangent line to this circle at the point P(3,4). First, we observe that the radius is a segment of the line passing through the origin (0, 0) and P(3,4), and its equation is (why?). Since the tangent line is perpendicular to this line, its slope is -3/4 and passes through P(3, 4), using the point-slope formula, its equation is found to be Let us compute y-values on both the tangent line and the circle for x-values near the point P(3, 4). Note that near P, we can solve for the y-value on the upper half of the circle which is found to be When x = 3.01, we find the y-value on the tangent line is y = -3/4(3.01) + 25/4 = 3.9925, while the corresponding value on the circle is (Note that the tangent line lie above the circle, so its y-value was expected to be a larger.) In Table 1, we indicate other corresponding values as we vary x near P.
    [Show full text]
  • And Are Congruent Chords, So the Corresponding Arcs RS and ST Are Congruent
    9-3 Arcs and Chords ALGEBRA Find the value of x. 3. SOLUTION: 1. In the same circle or in congruent circles, two minor SOLUTION: arcs are congruent if and only if their corresponding Arc ST is a minor arc, so m(arc ST) is equal to the chords are congruent. Since m(arc AB) = m(arc CD) measure of its related central angle or 93. = 127, arc AB arc CD and . and are congruent chords, so the corresponding arcs RS and ST are congruent. m(arc RS) = m(arc ST) and by substitution, x = 93. ANSWER: 93 ANSWER: 3 In , JK = 10 and . Find each measure. Round to the nearest hundredth. 2. SOLUTION: Since HG = 4 and FG = 4, and are 4. congruent chords and the corresponding arcs HG and FG are congruent. SOLUTION: m(arc HG) = m(arc FG) = x Radius is perpendicular to chord . So, by Arc HG, arc GF, and arc FH are adjacent arcs that Theorem 10.3, bisects arc JKL. Therefore, m(arc form the circle, so the sum of their measures is 360. JL) = m(arc LK). By substitution, m(arc JL) = or 67. ANSWER: 67 ANSWER: 70 eSolutions Manual - Powered by Cognero Page 1 9-3 Arcs and Chords 5. PQ ALGEBRA Find the value of x. SOLUTION: Draw radius and create right triangle PJQ. PM = 6 and since all radii of a circle are congruent, PJ = 6. Since the radius is perpendicular to , bisects by Theorem 10.3. So, JQ = (10) or 5. 7. Use the Pythagorean Theorem to find PQ.
    [Show full text]
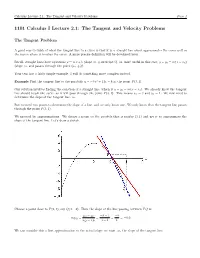
  • 1101 Calculus I Lecture 2.1: the Tangent and Velocity Problems
    Calculus Lecture 2.1: The Tangent and Velocity Problems Page 1 1101 Calculus I Lecture 2.1: The Tangent and Velocity Problems The Tangent Problem A good way to think of what the tangent line to a curve is that it is a straight line which approximates the curve well in the region where it touches the curve. A more precise definition will be developed later. Recall, straight lines have equations y = mx + b (slope m, y-intercept b), or, more useful in this case, y − y0 = m(x − x0) (slope m, and passes through the point (x0, y0)). Your text has a fairly simple example. I will do something more complex instead. Example Find the tangent line to the parabola y = −3x2 + 12x − 8 at the point P (3, 1). Our solution involves finding the equation of a straight line, which is y − y0 = m(x − x0). We already know the tangent line should touch the curve, so it will pass through the point P (3, 1). This means x0 = 3 and y0 = 1. We now need to determine the slope of the tangent line, m. But we need two points to determine the slope of a line, and we only know one. We only know that the tangent line passes through the point P (3, 1). We proceed by approximations. We choose a point on the parabola that is nearby (3,1) and use it to approximate the slope of the tangent line. Let’s draw a sketch. Choose a point close to P (3, 1), say Q(4, −8).
    [Show full text]
  • Circle Theorems
    Circle theorems A LEVEL LINKS Scheme of work: 2b. Circles – equation of a circle, geometric problems on a grid Key points • A chord is a straight line joining two points on the circumference of a circle. So AB is a chord. • A tangent is a straight line that touches the circumference of a circle at only one point. The angle between a tangent and the radius is 90°. • Two tangents on a circle that meet at a point outside the circle are equal in length. So AC = BC. • The angle in a semicircle is a right angle. So angle ABC = 90°. • When two angles are subtended by the same arc, the angle at the centre of a circle is twice the angle at the circumference. So angle AOB = 2 × angle ACB. • Angles subtended by the same arc at the circumference are equal. This means that angles in the same segment are equal. So angle ACB = angle ADB and angle CAD = angle CBD. • A cyclic quadrilateral is a quadrilateral with all four vertices on the circumference of a circle. Opposite angles in a cyclic quadrilateral total 180°. So x + y = 180° and p + q = 180°. • The angle between a tangent and chord is equal to the angle in the alternate segment, this is known as the alternate segment theorem. So angle BAT = angle ACB. Examples Example 1 Work out the size of each angle marked with a letter. Give reasons for your answers. Angle a = 360° − 92° 1 The angles in a full turn total 360°. = 268° as the angles in a full turn total 360°.
    [Show full text]
  • Squaring the Circle in Elliptic Geometry
    Rose-Hulman Undergraduate Mathematics Journal Volume 18 Issue 2 Article 1 Squaring the Circle in Elliptic Geometry Noah Davis Aquinas College Kyle Jansens Aquinas College, [email protected] Follow this and additional works at: https://scholar.rose-hulman.edu/rhumj Recommended Citation Davis, Noah and Jansens, Kyle (2017) "Squaring the Circle in Elliptic Geometry," Rose-Hulman Undergraduate Mathematics Journal: Vol. 18 : Iss. 2 , Article 1. Available at: https://scholar.rose-hulman.edu/rhumj/vol18/iss2/1 Rose- Hulman Undergraduate Mathematics Journal squaring the circle in elliptic geometry Noah Davis a Kyle Jansensb Volume 18, No. 2, Fall 2017 Sponsored by Rose-Hulman Institute of Technology Department of Mathematics Terre Haute, IN 47803 a [email protected] Aquinas College b scholar.rose-hulman.edu/rhumj Aquinas College Rose-Hulman Undergraduate Mathematics Journal Volume 18, No. 2, Fall 2017 squaring the circle in elliptic geometry Noah Davis Kyle Jansens Abstract. Constructing a regular quadrilateral (square) and circle of equal area was proved impossible in Euclidean geometry in 1882. Hyperbolic geometry, however, allows this construction. In this article, we complete the story, providing and proving a construction for squaring the circle in elliptic geometry. We also find the same additional requirements as the hyperbolic case: only certain angle sizes work for the squares and only certain radius sizes work for the circles; and the square and circle constructions do not rely on each other. Acknowledgements: We thank the Mohler-Thompson Program for supporting our work in summer 2014. Page 2 RHIT Undergrad. Math. J., Vol. 18, No. 2 1 Introduction In the Rose-Hulman Undergraduate Math Journal, 15 1 2014, Noah Davis demonstrated the construction of a hyperbolic circle and hyperbolic square in the Poincar´edisk [1].
    [Show full text]
  • Angles ANGLE Topics • Coterminal Angles • Defintion of an Angle
    Angles ANGLE Topics • Coterminal Angles • Defintion of an angle • Decimal degrees to degrees, minutes, seconds by hand using the TI-82 or TI-83 Plus • Degrees, seconds, minutes changed to decimal degree by hand using the TI-82 or TI-83 Plus • Standard position of an angle • Positive and Negative angles ___________________________________________________________________________ Definition: Angle An angle is created when a half-ray (the initial side of the angle) is drawn out of a single point (the vertex of the angle) and the ray is rotated around the point to another location (becoming the terminal side of the angle). An angle is created when a half-ray (initial side of angle) A: vertex point of angle is drawn out of a single point (vertex) AB: Initial side of angle. and the ray is rotated around the point to AC: Terminal side of angle another location (becoming the terminal side of the angle). Hence angle A is created (also called angle BAC) STANDARD POSITION An angle is in "standard position" when the vertex is at the origin and the initial side of the angle is along the positive x-axis. Recall: polynomials in algebra have a standard form (all the terms have to be listed with the term having the highest exponent first). In trigonometry, there is a standard position for angles. In this way, we are all talking about the same thing and are not trying to guess if your math solution and my math solution are the same. Not standard position. Not standard position. This IS standard position. Initial side not along Initial side along negative Initial side IS along the positive x-axis.
    [Show full text]
  • 20. Geometry of the Circle (SC)
    20. GEOMETRY OF THE CIRCLE PARTS OF THE CIRCLE Segments When we speak of a circle we may be referring to the plane figure itself or the boundary of the shape, called the circumference. In solving problems involving the circle, we must be familiar with several theorems. In order to understand these theorems, we review the names given to parts of a circle. Diameter and chord The region that is encompassed between an arc and a chord is called a segment. The region between the chord and the minor arc is called the minor segment. The region between the chord and the major arc is called the major segment. If the chord is a diameter, then both segments are equal and are called semi-circles. The straight line joining any two points on the circle is called a chord. Sectors A diameter is a chord that passes through the center of the circle. It is, therefore, the longest possible chord of a circle. In the diagram, O is the center of the circle, AB is a diameter and PQ is also a chord. Arcs The region that is enclosed by any two radii and an arc is called a sector. If the region is bounded by the two radii and a minor arc, then it is called the minor sector. www.faspassmaths.comIf the region is bounded by two radii and the major arc, it is called the major sector. An arc of a circle is the part of the circumference of the circle that is cut off by a chord.
    [Show full text]
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]
  • Geometry Course Outline
    GEOMETRY COURSE OUTLINE Content Area Formative Assessment # of Lessons Days G0 INTRO AND CONSTRUCTION 12 G-CO Congruence 12, 13 G1 BASIC DEFINITIONS AND RIGID MOTION Representing and 20 G-CO Congruence 1, 2, 3, 4, 5, 6, 7, 8 Combining Transformations Analyzing Congruency Proofs G2 GEOMETRIC RELATIONSHIPS AND PROPERTIES Evaluating Statements 15 G-CO Congruence 9, 10, 11 About Length and Area G-C Circles 3 Inscribing and Circumscribing Right Triangles G3 SIMILARITY Geometry Problems: 20 G-SRT Similarity, Right Triangles, and Trigonometry 1, 2, 3, Circles and Triangles 4, 5 Proofs of the Pythagorean Theorem M1 GEOMETRIC MODELING 1 Solving Geometry 7 G-MG Modeling with Geometry 1, 2, 3 Problems: Floodlights G4 COORDINATE GEOMETRY Finding Equations of 15 G-GPE Expressing Geometric Properties with Equations 4, 5, Parallel and 6, 7 Perpendicular Lines G5 CIRCLES AND CONICS Equations of Circles 1 15 G-C Circles 1, 2, 5 Equations of Circles 2 G-GPE Expressing Geometric Properties with Equations 1, 2 Sectors of Circles G6 GEOMETRIC MEASUREMENTS AND DIMENSIONS Evaluating Statements 15 G-GMD 1, 3, 4 About Enlargements (2D & 3D) 2D Representations of 3D Objects G7 TRIONOMETRIC RATIOS Calculating Volumes of 15 G-SRT Similarity, Right Triangles, and Trigonometry 6, 7, 8 Compound Objects M2 GEOMETRIC MODELING 2 Modeling: Rolling Cups 10 G-MG Modeling with Geometry 1, 2, 3 TOTAL: 144 HIGH SCHOOL OVERVIEW Algebra 1 Geometry Algebra 2 A0 Introduction G0 Introduction and A0 Introduction Construction A1 Modeling With Functions G1 Basic Definitions and Rigid
    [Show full text]