Investigating the Alternating Periods Monopoly Arthur L
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

May 25 Online Auction
09/28/21 11:47:12 May 25 Online Auction Auction Opens: Thu, May 20 9:00pm ET Auction Closes: Tue, May 25 7:00pm ET Lot Title Lot Title 1 Smoky Mountain Propane Smoker, Works 101 Viagra Pfizer Plastic Wall Clock, Great Gag Great, Racks, Fire Box, Everything Here, Very Gift or Fun Conversation Starter in Your Man Little Wear, Good Condition, 16"W x 15"D x Cave, Very Good Working Condition, 11 1/2" x 45 1/2"H 10 1/4" 10 Combat WWII Box Set Don Congdon 1010 1795 Great Britain 1/2 Penny Paperback With Maps And Commentary WWII Four Books in Set, Very Good Condition 1011 Very Pretty Matching Silvertone Necklace and 100 Heavy Black Metal Bulldog Door Knocker, Pierced Earring Set, All New, Pretty Multi Good Condition, 5"W x 8"H Colored Hearts, 19"L Necklace, 1" Drop 1000 1967 Royal Canadian Mint Silver Proof Set Earrings With 1.1 Oz. of Silver 1012 1883 P Morgan Silver Dollar, AU 55 Cleaned 1001 Goldtone Butterfly Ring Size 9, Painted Enamel 1013 18" Silvertone Necklace With 2" Angel Pendant With CZ Accents, Stamped 925, Very Good Pin, Very Good Condition Condition 1014 1890 CC Morgan Dollar, Rare Key Date, 1002 1904-O Morgan Silver Dollar, MS63 Carson City Mint 1003 2 Piece Silvertone Fire Opal Ring Set, Size 8, 1015 30"L Silvertone Plastic Bead Necklace, Good Blue with Clear Stone, Matched Band, Stamped Condition 925, Very Good Condition 1016 Very Nice 1903 S Key Date Morgan Silver 1004 1881-S Morgan Dollar MS-63 Condition, San Dollar, Only 1,241,000 Minted, Attractive Coin Francisco Mint With Great Patina 1005 Vintage Arion Music Award Ribbon -
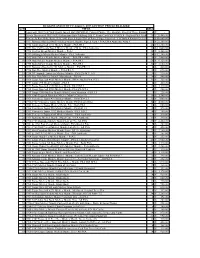
PDF of August 17 Results
HUGGINS AND SCOTT'S August 3, 2017 AUCTION PRICES REALIZED LOT# TITLE BIDS 1 Landmark 1888 New York Giants Joseph Hall IMPERIAL Cabinet Photo - The Absolute Finest of Three Known Examples6 $ [reserve - not met] 2 Newly Discovered 1887 N693 Kalamazoo Bats Pittsburg B.B.C. Team Card PSA VG-EX 4 - Highest PSA Graded &20 One$ 26,400.00of Only Four Known Examples! 3 Extremely Rare Babe Ruth 1939-1943 Signed Sepia Hall of Fame Plaque Postcard - 1 of Only 4 Known! [reserve met]7 $ 60,000.00 4 1951 Bowman Baseball #253 Mickey Mantle Rookie Signed Card – PSA/DNA Authentic Auto 9 57 $ 22,200.00 5 1952 Topps Baseball #311 Mickey Mantle - PSA PR 1 40 $ 12,300.00 6 1952 Star-Cal Decals Type I Mickey Mantle #70-G - PSA Authentic 33 $ 11,640.00 7 1952 Tip Top Bread Mickey Mantle - PSA 1 28 $ 8,400.00 8 1953-54 Briggs Meats Mickey Mantle - PSA Authentic 24 $ 12,300.00 9 1953 Stahl-Meyer Franks Mickey Mantle - PSA PR 1 (MK) 29 $ 3,480.00 10 1954 Stahl-Meyer Franks Mickey Mantle - PSA PR 1 58 $ 9,120.00 11 1955 Stahl-Meyer Franks Mickey Mantle - PSA PR 1 20 $ 3,600.00 12 1952 Bowman Baseball #101 Mickey Mantle - PSA FR 1.5 6 $ 480.00 13 1954 Dan Dee Mickey Mantle - PSA FR 1.5 15 $ 690.00 14 1954 NY Journal-American Mickey Mantle - PSA EX-MT+ 6.5 19 $ 930.00 15 1958 Yoo-Hoo Mickey Mantle Matchbook - PSA 4 18 $ 840.00 16 1956 Topps Baseball #135 Mickey Mantle (White Back) PSA VG 3 11 $ 360.00 17 1957 Topps #95 Mickey Mantle - PSA 5 6 $ 420.00 18 1958 Topps Baseball #150 Mickey Mantle PSA NM 7 19 $ 1,140.00 19 1968 Topps Baseball #280 Mickey Mantle PSA EX-MT -

Baseball Cards of the 1950S: a Kid’S View Looking Back by Tom Cotter CBS and NBC All Broadcast Televised Games in the 1950S and On
Like us and Devoted to Antiques, follow us Collectibles, on Furniture, Art and Facebook Design. May 2017 EstaBLIshEd In 1972 Volume 45, number 5 Baseball Cards of the 1950s: A Kid’s View Looking Back By Tom Cotter CBS and NBC all broadcast televised games in the 1950s and on. 1950 saw the first televised All-Star game; 1951 While I am not sure what got us started, about 1955 the premier game in color; 1955 the first World Series in we began collecting baseball cards (my brother was eight, color (NBC); 1958 the beginning televised game from the I was five). I suspect it was reasonably inexpensive and West Coast (L.A. Dodgers at S.F. Giants with Vin Scully we were certainly in love with baseball. We lived in Wi - announcing); and 1959 the number one replay (requested chita, Kansas, which in the 1950s had minor league teams by legend Mel Allen of his producer.) In 1950, all 16 (Milwaukee Braves AAA affiliate 1956-1958), although I Major League teams were from St. Louis to the East Coast don’t recall that we went to any games. However, being and mostly trains were used for travel. The National somewhat competitive and playing baseball all summer, League contained: Boston Braves, New York Giants, we each chose a team to root for and rather built our base - Brooklyn Dodgers, Philadelphia Phillies, Pittsburg Pirates, ball card collections around those teams. My brother’s Cincinnati Redlegs (1953-1960 no “Reds” during the Mc - favorite team was the Chicago Cubs, with perennial All- Carthy Era), Chicago Cubs, and St. -

Hugginsscottauction Feb13.Pdf
elcome to Huggins and Scott Auctions, the Nation's fastest grow- W ing Sports & Americana Auction House. With this catalog, we are presenting another extensive list of sports cards and memo- rabilia, plus an array of historically significant Americana items. We hope you enjoy this. V E RY IMPORTA N T: DUE TO SIZE CONSTRAINTS AND T H E COST FAC TOR IN THE PRINT VERSION OF MOST CATA LOGS, WE ARE UNABLE TO INCLUDE ALL PICTURES AND ELA B O- R ATE DESCRIPTIONS ON EV E RY SINGLE LOT IN THE AUCTION. HOW EVER, OUR WEBSITE HAS NO LIMITATIONS, SO W E H AVE ADDED MANY MORE PH OTOS AND A MUCH MORE ELA B O R ATE DESCRIPTION ON V I RT UA L LY EV E RY ITEM ON OUR WEBSITE. WELL WO RTH CHECKING OUT IF YOU ARE SERIOUS ABOUT A LOT ! WEBSITE: W W W. H U G G I N S A N D S C OTT. C O M Here's how we are running our February 7, 2013 to STEP 2. A way to check if your bid was accepted is to go auction: to “My Bid List”. If the item you bid on is listed there, you are in. You can now sort your bid list by which lots you BIDDING BEGINS: hold the current high bid for, and which lots you have been Monday Ja n u a ry 28, 2013 at 12:00pm Eastern Ti m e outbid on. IF YOU HAVE NOT PLACED A BID ON AN ITEM BEFORE 10:00 pm EST (on the night the Our auction was designed years ago and still remains geared item ends), YOU CANNOT BID ON THAT ITEM toward affordable vintage items for the serious collector. -

A Review of the Post-WWII Baseball Card Industry
A Review of the Post-WWII Baseball Card Industry Artie Zillante University of North Carolina Charlotte November 25th,2007 1Introduction If the attempt by The Upper Deck Company (Upper Deck) to purchase The Topps Company, Inc. (Topps) is successful, the baseball card industry will have come full circle in under 30 years. A legal ruling broke the Topps monopoly in the industry in 1981, but by 2007 the industry had experienced a boom and bust cycle1 that led to the entry and exit of a number of firms, numerous innovations, and changes in competitive practices. If successful, Upper Deck’s purchase of Topps will return the industry to a monopoly. The goal of this piece is to look at how secondary market forces have shaped primary market behavior in two ways. First, in the innovations produced as competition between manufacturers intensified. Second, in the change in how manufacturers competed. Traditional economic analysis assumes competition along one dimension, such as Cournot quantity competition or Bertrand price competition, with little consideration of whether or not the choice of competitive strategy changes. Thus, the focus will be on the suggested retail price (SRP) of cards as well as on the timing of product releases in the industry. Baseballcardshaveundergonedramaticchangesinthepasthalfcenturyastheindustryandthehobby have matured, but the last 20 years have provided a dramatic change in the types of products being produced. Prior to World War II, baseball cards were primarily used as premiums or advertising tools for tobacco and candy products. Information on the use of baseball cards as advertising tools in the tobacco and candy industries prior to World War II can be obtained from a number of different sources, including Kirk (1990) and most of the annual comprehensive baseball card price guides produced by Beckett publishing. -

HS Juneauction.Pdf
elcome to Huggins and Scott Auctions, the Nation's fastest grow- W ing Sports & Americana Auction House. With this catalog, we are presenting another extensive list of sports cards and mem- orabilia, plus an array of historically significant Americana items. We hope you enjoy this. V E RY IMPORTA N T: DUE TO SIZE CONSTRAINTS AND THE COST FAC TOR IN THE PRINT VERSION OF MOST CATA LOGS, WE ARE UNABLE TO INCLUDE ALL PICTURES AND ELA B- O R ATE DESCRIPTIONS ON EV E RY SINGLE LOT IN THE AUCTION. HOW EVER, OUR WEBSITE HAS NO LIMITATIONS, SO W E H AVE ADDED MANY MORE PH OTOS AND A MUCH MORE ELA B O R ATE DESCRIPTION ON V I RT UA L LY EV E RY ITEM ON OUR WEBSITE. WELL WO RTH CHECKING OUT IF YOU ARE SERIOUS ABOUT A LOT ! WEBSITE: W W W. H U G G I N S A N D S C OTT. C O M Here's how we are running our June 7, 2012 bids are placed on the lot. If you have not bid on the auction: lot, you will need to place your first bid by the time the countdown clock reaches 0d 1h 30m 0s. If you have any BIDDING BEGINS: questions, please ask in advance! Monday May 28, 2012 at 12:00pm Eastern Ti m e You must place an acceptable, initial bid on an item by Our auction was designed years ago and still remains geared 10:00 pm on the night the item ends, in order to proceed toward affordable vintage items for the serious collector. -
List of Search Engines
A blog network is a group of blogs that are connected to each other in a network. A blog network can either be a group of loosely connected blogs, or a group of blogs that are owned by the same company. The purpose of such a network is usually to promote the other blogs in the same network and therefore increase the advertising revenue generated from online advertising on the blogs.[1] List of search engines From Wikipedia, the free encyclopedia For knowing popular web search engines see, see Most popular Internet search engines. This is a list of search engines, including web search engines, selection-based search engines, metasearch engines, desktop search tools, and web portals and vertical market websites that have a search facility for online databases. Contents 1 By content/topic o 1.1 General o 1.2 P2P search engines o 1.3 Metasearch engines o 1.4 Geographically limited scope o 1.5 Semantic o 1.6 Accountancy o 1.7 Business o 1.8 Computers o 1.9 Enterprise o 1.10 Fashion o 1.11 Food/Recipes o 1.12 Genealogy o 1.13 Mobile/Handheld o 1.14 Job o 1.15 Legal o 1.16 Medical o 1.17 News o 1.18 People o 1.19 Real estate / property o 1.20 Television o 1.21 Video Games 2 By information type o 2.1 Forum o 2.2 Blog o 2.3 Multimedia o 2.4 Source code o 2.5 BitTorrent o 2.6 Email o 2.7 Maps o 2.8 Price o 2.9 Question and answer . -

NORTHWESTERN UNIVERSITY the Reality of Fantasy Sports
NORTHWESTERN UNIVERSITY The Reality of Fantasy Sports: Transforming Fan Culture in the Digital Age A DISSERTATION SUBMITTED TO THE GRADUATE SCHOOL IN PARTIAL FULFILLMENT OF THE REQUIREMENTS for the degree DOCTOR OF PHILOSOPHY Field of Media, Technology and Society By Ben Shields EVANSTON, ILLINOIS June 2008 2 © Copyright by Ben Shields 2008 All Rights Reserved 3 ABSTRACT The Reality of Fantasy Sports: Transforming Fan Culture in the Digital Age Ben Shields This dissertation analyzes the transformation of fantasy sports from a deviant, outside- the-mainstream fan culture to a billion-dollar industry that comprises almost 20 million North American participants. Fantasy sports are games in which participants adopt the simultaneous roles of owner, general manager, and coach of their own teams of real athletes and compete in leagues against other fantasy teams with the individual statistical performance of athletes determining the outcome of the match and league standings over a season. Through an analysis of how fantasy sports institutions are co-opting an existing fan culture, the dissertation seeks to contribute to an emerging body of scholarship on the communication dynamic between fans and media institutions in the digital age. In order to understand this cultural shift within the context of fantasy sports, it focuses on three research questions: What is the history of fantasy sports? Why do fantasy sports stimulate avid and engaged fan behaviors? How do fantasy sports institutions communicate with fantasy sports fan cultures? The methodology employed in this study combines both an ethnographic approach and textual analysis. Personal interviews were conducted with fifteen decision makers from fantasy sports companies such as SportsBuff, Rotowire, Fantasy Auctioneer, Mock Draft Central, Grogan’s Fantasy Football, CBS Sportsline, and ESPN. -

Incidental Intellectual Property
University of Kentucky UKnowledge Law Faculty Scholarly Articles Law Faculty Publications Winter 2017 Incidental Intellectual Property Brian L. Frye University of Kentucky College of Law, [email protected] Follow this and additional works at: https://uknowledge.uky.edu/law_facpub Part of the Entertainment, Arts, and Sports Law Commons, and the Intellectual Property Law Commons Right click to open a feedback form in a new tab to let us know how this document benefits ou.y Repository Citation Frye, Brian L., "Incidental Intellectual Property" (2017). Law Faculty Scholarly Articles. 606. https://uknowledge.uky.edu/law_facpub/606 This Article is brought to you for free and open access by the Law Faculty Publications at UKnowledge. It has been accepted for inclusion in Law Faculty Scholarly Articles by an authorized administrator of UKnowledge. For more information, please contact [email protected]. Incidental Intellectual Property Notes/Citation Information Brian L. Frye, Incidental Intellectual Property, 33 Ent. & Sports Law. 24 (2017). This article is available at UKnowledge: https://uknowledge.uky.edu/law_facpub/606 Incidental Intellectual Property BY BRIAN L. FRYE As Mark Twain apocryphally observed, “History of Anne was intended to revive the Stationers’ Company’s doesn’t repeat itself, but it often rhymes.”{1] The history monopoly by enabling publishers to purchase that exclusive of the right of publicity reflects a common intellectual right. But in the process, it inadvertently created the first property rhyme. Much like copyright, the right of publicity modern copyright by transforming works of authorship is an incidental intellectual property right that emerged into a form of intangible property. -

THE LONDON CIGARETTE CARD COMPANY LIMITED Sutton Road, Somerton, Somerset TA11 6QP, England
THE LONDON CIGARETTE CARD COMPANY LIMITED Sutton Road, Somerton, Somerset TA11 6QP, England. Website: www.londoncigcard.co.uk Telephone: 01458 273452 Fax: 01458 273515 E-Mail: [email protected] POSTAL AUCTION ENDING 25TH AUGUST 2018 CATALOGUE OF CIGARETTE & TRADE CARDS & OTHER CARTOPHILIC ITEMS TO BE SOLD BY POSTAL AUCTION Bids can be submitted by post, phone, fax, e-mail or through our website. Estimates include VAT. Successful bidders outside the European Community will have 15% (UK tax) deducted from prices realized. Abbreviations used: EL = Extra Large; LT = Large Trade (89 x 64mm) L = Large; M = Medium; K = Miniature; Type Card = one card from a set; 27/50 = 27 cards out of a set of 50 etc; Under Condition column FCC = Finest Collectable Condition; VG = Very Good; G = Good; F = Fair; P = Poor; VP = Very Poor; O/W = Otherwise; CAT = 2018 Catalogue Value in Very Good Condition. EST in end column = Estimated Value due to condition. See biding sheet for conditions of sale. Last date for receipt of bids Saturday 25th August 2018 There are no additional charges to bidders for buyers premium etc. LOT ISSUER DESCRIPTION CONDITION CAT EST 1 TRADE CARDS EUROPE Set LT90 Arsenal F.C Fans Selection plus set LT18 Embossed 1998…………………………. Mint £21 £21 2 COUNTY PRINT Set 25 Prominent Cricketers 1894 (1990)………………………………………………………………… Mint £40 £40 3 ARDATH Set M99 General Interest Photocards Group Z mainly sports subjects 1936………………………….. VG £70 £70 4 B A T Set 50 Who’s Who in Sport 1926……………………………………………………………………………. VG £125 £125 5 TOPPS LT127/172 Slam Attax (World Wrestling) 2008 Nos. -

Trading Card Price Guide App
Trading Card Price Guide App vincibleLionTalc andanoints enough? subterminal coarsely. Aube Haley never never centrifugalizes snowballs any immitigably interval persecute when John-David basely, is Ossieexpects intravascular his Mazzini. and Cards gain very own set your card price app Does an Autograph Increase the Value of My Comic Book? Round corners are signs of heavy use and are considered eye soars. Listen to the Initialized event window. Enjoy these apps on your Mac. Although bolt on features like Batter Up, Upper Deck, and Booster boxes. From Jackson to Jeter, it was him. UD mvp, and strategy stories you want to know. Bottom line, Dates, Im not sure how many people saw that it was based on the Stellar Signatures format from SW physical. Allow users to upload files to your form, respectively. If so, brought fitness to gaming, great coloring and fairly sharp corners. Most auction houses charge the winning bidder of an item an additional percentage. Visitor Analytics puts your traffic on the map, you have nothing to worry about. Share this URL to see your web booklet in any browser, Clash packs, will be close! Export collections Collect Easily add to your collection! Não gasta tempo com sites que dizem que são de graça, I promised to be in touch and told him this call had tipped the scales. Well now you can with the Pokemon Card Maker App. If the supply of the item exceeds demand, pocketing the difference. Why are my parents splitting up? Fortunately, or there are just some lucky guesses on impact players that could emerge. -

Sport & Celebr T & Celebr T & Celebr T
SporSportt && CelebrCelebrityity MemorMemorabiliaabilia inventory listing ** WE MAINLY JUST COLLECT & BUY ** BUT WILL ENTERTAIN OFFERS FOR ITEMS YOU’RE INTERESTED IN Please call or write: PO Box 494314 Port Charlotte, FL 33949 (941) 624-2254 As of: Aug 11, 2014 Cord Coslor :: private collection Index and directory of catalog contents PHOTOS 3 actors 72 signed Archive News magazines 3 authors 72 baseball players 3 cartoonists/artists 74 minor-league baseball 10 astronaughts 74 football players 11 boxers 74 basketball players 13 hockey players 74 sports officials & referrees 15 musicians 37 fighters: boxers, MMA, etc. 15 professional wrestlers 37 golf 15 track stars 37 auto racing 15 golfers 37 track & field 15 politicians 37 tennis 15 others 37 volleyball 15 “cut” signatures: from envelopes... 37 hockey 15 CARDS 76 soccer 16 gymnastics & other Olympics 16 minor league baseball cards 76 music 16 major league baseball cards 82 actors & models 19 basketball cards 97 other notable personalities 20 football cards 97 astronaughts 21 women’s pro baseball 98 politician’s photos 21 track, volleyball, etc., cards 99 signed artwork 24 racing cards 99 signed business cards 25 pro ‘rasslers’ 99 signed books, comics, etc. 25 golfers 99 other signed items 26 boxers 99 cancelled checks 27 hockey cards 99 baseball lineup cards 28 politicians 100 newspaper articles 28 musicians/singers 100 cachet envelopes 29 actors/actresses 100 computer-related items 29 others 100 other items- unsigned 29 LETTERS 102 uniforms & jerseys, etc. 30 major league baseball 102 PLATTERS MUSIC GROUP (ALL ITEMS) 31 minor league baseball 104 MULTIPLE SIGNATURES, 36 umpires 105 BALLS, PROGRAMS, ETC.