DOCSLIB.ORG

N76 11 0 23 Preceding Page Blank

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
N76 11 0 23 Preceding Page Blank https://ntrs.nasa.gov/search.jsp?R=19760003935 2020-03-20T01:23:55+00:00Z View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by NASA Technical Reports Server N76 11 0 23 8.2(][) Drag of the Complete Configuration Aerodynamic Conslderat ions Jan Roskam University of Kansas Introduct ion The purpose of this part of the paper is to focus on a number of drag items and relate them to the performance of the complete configuration. First, the effect of fuselage camber, wing and nacelle incidence are discussed from a viewpoint of design decision making. Second, the effect of overall cruise drag on the design gross and empty weight of the airplane is discussed. Examples show that cruise drag can have a very important influence on total airplane weight. Third, the effects of usable cruise lift-to-drag ratio and wing-loading are shown to be important. Finally several research needs relating to design of the complete configuration are reviewed. Effect of Fuselage Camber, Wing and Nacelle Incidence in putting together a new airplane1 a number of fundamental geometric choices must be made. Typical examples of such choices are: - extent of fuselage camber; - wing incidence on fuselage; and - nacelle incidence and position relative to the wing. In determ;ning the extent of wind tunnel testing required to "optimize" the configuration, the aerodynamiclst is confronted with a large number of variables. For example, if it is assumed, that two camber shapes, two wing-fuselage incidence angles and two wing-nacelle incidence angles are to be investigated, this alone leads to eight combinations to be tested. Under the economic constraints of the general aviation industry it is usually not feasible to do this much testing. Major aircraft manufacturers, on fighter, bomber and even on some tTans- port programs, obtain significant inputs from NASA in terms of systematic wind tunnel configuration testing. How does the general aviation designer choose the best configuration ? Well, very often he ends up guessin_ or, the shaping decision (for lack of definitive aerodynamic input) is made for him by engineers or managers outside of aerodynamics. Preceding Page Blank Inputs such as tooling costs and marketing opinions outweigh the aerodynamlcist in the decislon making process, primarily because the aerodynamlclst does not have convlnclng arguments one way or the other. To illustrate these points and to point once more to the need for systematic tunnel testing of general aviation research models, the following examples are given. Note from Figure 1 that three different vertical nacelle installations are being used for turbopropeller airplanes. Note also, that all three use rather differing aft fairing shapes. The question arises: can they all be right? Observe from Figure 2 that one manufacturer employs two quite different piston engine nacelle configurations. Figure 3 illustrates two more and again different nacelle shapes. The questions arises again: can they all be rlght? Possible pay-offs of such research are illustrated in Figure 4 taken from Reference 1 (1942). Figure 4 shows a range of wing-body-nacelle drag coefficients of .1250 to .1050, (.0078 to .0066 based on wing areal) dependlng on vertical nacelle location alone. In other words, there are 12 drag counts to be galned by selecting the vertical nacelle location. It would seem that the industry could derive significant beneflts from a series of systematic wind tunnel test to determine the best (lowest drag) shape of such wing-nacelle installations. Such research should also account for the effect of thrustline location and orientation, as well as for the possible beneficial effect of forward propeller shaft extensions, such as used on the hlavajo. Drag Effect on Airplane Weight and Airplane Market Price Aerodynamic drag is not generally thought of in general aviation airplane design as an important factor affecting airplane weight. The reason may be the fact that usually new airplane "designs" consist of adaptations of components which are already in production, to a new alrplane. The term "tinker toying", although not a kind description probably applies to much of general aviation airplane design. However, every now and then a truly new design evolves and then the effect of drag on weight can be important as will be illustrated in the following simplified analysls. Assume that total airplane weight is broken down as follows: W = WpL + W F + W E (1) 338 whe re: WpL - payload weight W F = fuel weight (including reserves) W E = empty weight Fuel weight and empty weight are assumed to be broken down as follows: W F = A + TxSFC x _ and: (2) R W E = B" +'CT + D'WF (3) whe re: A = weight of reserve fuel T = cruise thrust SFC = cruise fuel consumption Ibs/lbs/hr V = cruise speed R = cruise range B = empty weight without power plant and fuel system = weight of power plant per Ibs of cruise thrust D = weight of fuel system per Ibs of cruise fuel In cruise flight: T = W and L = D (4) I ift drag so that T = W(D) (5) Substituting equations (2) through (5) into equation (1) yields: Upon solving for W it is found that: VU_,t. +-A, t !_ .,,. "_ W _ ,,, or 339 By introducing: it is possibleto rewrite equation (7) as: _kJ_ o_ - b//%.j_ D To determine the effect of drag on airplane weight, the differential can be found from equation (10) as: bk_J --4 b = CV=- 0 0 Table 1 presents data from which ;>_/'J_ can be calculated for a typical general aviation piston engine driven twin. So using equation (11): "_ Ud = OI- z L 32- _ - Itq This means that per unit L/D, the airplane gross weight can be lowered by about 120 Ibs, a significant saving when compared to ff_e empty weight, W E- Figures 5 and 6 illustrate similar results obtained in Reference 2 on small two-place turbofan (1200 Ibs max thrust) airplanes. Table 1 and Figure 5 and 6 all show the importance of designing to the maximum possible cruise lift-to-drag ratio, if the lowest possible airplane weight is to be achieved. It should be noted, that lower empty weight, achieved by better aerodynamic design has a very significant effect on the marketing price of an airplane. Table 2 shows typical market prices related to gross and empty weights for general aviation twins. For the example twin of Table 1 the typical market price per pound of empty weight would be about 34 $/Ibs. Attaining a 120 Ibs saving would cut the market price by $4,080, a rather significant competitive advantage l 340 Table 1. Data for Calculation of_/_(,LIzI)_ for a Typical Twin. WE = 3700 Ibs Engines 2 x 300 hp. at 450 Ibs each WF = lO00 Ibs WpL = 1600 Ibs SFChp = .45 Ibs/hp/hrs W = 6300 Ibs Assume propeller and engine weight =llO0 Ibs Assume fuel system weight = lO0 Ibs Assuming a cruise L/D = II and Wave = 5,800 Ibs cruise T cruise = 527 Ibs Assume Vcruise = 216 mph, then HPcruise = 303 Fuel flow in cruise then is 136 Ibs/hr. This yields a range of (1000-200 (reserves)) 216 = 1270 miles The value of SFC is 136 136 5-,27= .26 lbs/Ibs/hr I So, A = 200 Ibs B = 3700-1200 = 2500 Ibs - IlO0 - 1O0 C - 527-" = 2.1 D = 1,000-200 = .13 From equations (8) and (9): a = 1600 + 200 (l + .13) + 2500 = 4326 Ibs b ,26 x T_ (l + .13) + 2.1 = .05 + 2.1 = 2.15 Lift-to-Drag Ratio and Wing Loading Effects Revisited Light airplanes, such as the Cessna 172 typically cruise at lift coefficients in the range of. C. _ .3 -Eo ._-- Figure 7 shows that the corresponding L/D value varies from 10.0 to 13.2. This compares with a maximum L/D value of 13.8 indicating that significant improvements must be attainable by increasing wing loading. Increasing wing loading not only will bring the cruise C L closer to I/D/max on the polar but it will also shift the polar to 341 Table 2. Typical General Aviation Light Twin Airframe Prices, (1975 Flying Annual Data) GrossWeight Empty Weight Price Price Price T Type w (Ibs) wE (Ibs] $/lbs i' $/Ibs Cessna Skymaster 4,630 2,710 63,300 13.7 23.4 Piper Seneca 4,570 2,770 63,995 14.0 23.1 Piper Aztec E 5,200 3,042 88,200 17.0 29.0 Beech Baron B55 5,100 3,155 89,000 17.5 28.2 Cessna 310 5,500 3,251 89,950 16.4 27.7 _J Averages 5,000 2,986 78,889 15.7 26.3 Rockwell Shrike Commander 6,750 4,608 128,150 19.0 27.8 Cessna 402 B 6,300 3,741 138,500 22.0 37.0 Piper Navajo B 6,500 3,930 13g,100 21.4 35.4 Cessna 414 6,350 4,042 17 4,950 27.6 43.3 Beech Duke 6,775 4,265 219,450 32.4 51.5 Averages 6,535 ! 4,117 160,030 24.5 i 39.0 342 the left in the higher C L range (note that CDo actually will increase because it is based on a smaller wing areal). This fact has been previously demonstrated also in such papers as References 3, 4, and 5. Figure 8 illustrates some typical results. Cutting wing area in the chordwlse direction by 30 percent results in a 10 percent reduction in thrust required and therefore _n fuel flow. F_gure 9, shows the relative aerodynamic "cleanness" of 1975 general aviation single engine airplanes compared to what is felt feasible in the future.
Load more

Recommended publications
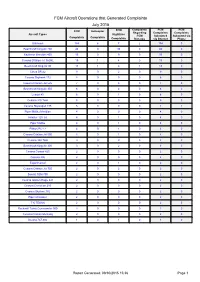
  • FCM Aircraft Operations That Generated Complaints July 2015
    FCM Aircraft Operations that Generated Complaints July 2015 Complaints FCM FCM FCM Helicopter FCM Regarding Complaints Complaints Aircraft Types Nighttime FCM Submitted Submitted via Complaints Complaints Complaints Run-ups via Internet Phone Unknown 184 6 7 2 184 0 Beechcraft King Air 200 46 0 30 0 46 0 Raytheon Beechjet 400 15 0 9 0 15 0 Cessna Citation Jet 560XL 15 1 4 0 15 0 Beechcraft King Air 90 13 1 6 1 13 0 Cirrus SR-22 9 0 2 0 9 0 Cessna Skyhawk 172 8 0 0 0 8 0 Cessna Citation Jet 525 7 0 3 0 7 0 Beechcraft King Air 350 6 0 2 0 6 0 Learjet 45 6 0 1 0 6 0 Cessna 310 Twin 5 0 0 0 5 0 Cessna Skywagon 185 5 0 0 0 4 1 Piper Malibu Meridian 4 0 0 0 4 0 Hawker 125 Jet 4 0 1 0 4 0 Piper Malibu 4 0 1 0 4 0 Pilatus PC-12 4 0 1 0 4 0 Cessna Citation Jet 560 4 0 1 0 4 0 Cessna 340 Twin 3 0 0 0 3 0 Beechcraft King Air 300 3 0 2 0 3 0 Cessna Corsair 425 2 0 0 0 2 0 Cessna 206 2 0 0 0 2 0 Experimental 2 0 1 0 2 0 Cessna Citation Jet 750 2 0 2 0 2 0 Socata TBM 700 2 0 0 0 2 0 Cessna Golden Eagle 421 2 0 0 0 2 0 Cessna Centurion 210 2 0 0 0 2 0 Cessna Skylane 182 2 0 0 0 2 0 Piper Cherokee 2 0 0 0 2 0 T-6 TEXAN 2 0 0 0 2 0 Rockwell Turbo Commander 900 2 0 0 0 2 0 Cessna Citation Mustang 2 0 0 0 2 0 Boeing 737-900 1 0 1 0 1 0 Report Generated: 09/30/2015 15:36 Page 1 Complaints FCM FCM FCM Helicopter FCM Regarding Complaints Complaints Aircraft Types Nighttime FCM Submitted Submitted via Complaints Complaints Complaints Run-ups via Internet Phone Piper Navajo Twin 1 0 0 0 1 0 Mitsubishi MU-2 1 0 0 0 1 0 Beechcraft Debonair/Bonanza 1 0 1 0 1 0
    [Show full text]
  • Top Turboprop Series: We Compare Popular Pre-Owned Models
    FOR THE PILOTS OF OWNER-FLOWN, CABIN-CLASS AIRCRAFT SEPTEMBER 2019 $3.95 US VOLUME 23 NUMBER 9 Top Turboprop Series: We Compare Popular Pre-Owned Models Five Questions The Latest on One Pilot’s with Corporate the Cessna Denali Introduction Angel Network & SkyCourier to Aerobatics Jet It US One year $15.00, two years $29.00 Canadian One year $24.00, two years $46.00 Overseas One Year $52.00, Two Years $99.00 Single copies $6.50 PRIVATE. FAST. SMART. EDITOR Rebecca Groom Jacobs SEPTEMBER2019 • VOL. 23, NO. 9 (316) 641-9463 Contents [email protected] EDITORIAL OFFICE 2779 Aero Park Drive 4 Traverse City, MI 49686 Editor’s Briefing Phone: (316) 641-9463 E-mail: [email protected] 2 A Career Shaped by Turboprops PUBLISHER by Rebecca Groom Jacobs Dave Moore PRESIDENT Position Report Dave Moore 4 What Makes a Turboprop CFO Safer? Answer: You Rebecca Mead PRODUCTION MANAGER by Dianne White Mike Revard PUBLICATIONS DIRECTOR Jake Smith GRAPHIC DESIGNER Marci Moon 6 TWIN & TURBINE WEBSITE 6 Top Turboprop Series: www.twinandturbine.com Pre-Owned Piper Meridian ADVERTISING DIRECTOR and Daher TBM 700C2 John Shoemaker Twin & Turbine by Joe Casey 2779 Aero Park Drive Traverse City, MI 49686 12 Five on the Fly with Phone: 1-800-773-7798 Corporate Angel Network Fax: (231) 946-9588 [email protected] by Rebecca Groom Jacobs ADVERTISING ADMINISTRATIVE COORDINATOR & REPRINT SALES 14 The Latest on the Betsy Beaudoin Cessna Denali and Phone: 1-800-773-7798 [email protected] SkyCourier ADVERTISING ADMINISTRATIVE by Rich Pickett ASSISTANT Jet It Erika Shenk 22 Intro to Aerobatics Phone: 1-800-773-7798 by Jared Jacobs [email protected] SUBSCRIBER SERVICES Rhonda Kelly Diane Smith Jamie Wilson Molly Costilow 22 Kelly Adamson P.O.
    [Show full text]
  • Aerodynamic Analysis and Design of a Twin Engine Commuter Aircraft
    28TH INTERNATIONAL CONGRESS OF THE AERONAUTICAL SCIENCES AERODYNAMIC ANALYSIS AND DESIGN OF A TWIN ENGINE COMMUTER AIRCRAFT Fabrizio Nicolosi*, Pierluigi Della Vecchia*, Salvatore Corcione* *Department of Aerospace Engineering - University of Naples Federico II [email protected]; [email protected], [email protected] Keywords: Aircraft Design, Commuter Aircraft, Aerodynamic Analysis Abstract 1. Introduction The present paper deals with the preliminary design of a general aviation Commuter 11 seat Many in the industry had anticipated 2011 to be aircraft. The Commuter aircraft market is today the year when the General Aviation characterized by very few new models and the manufacturing industry would begin to recover. majority of aircraft in operation belonging to However, the demand for business airplanes and this category are older than 35 years. Tecnam services, especially in the established markets of Aircraft Industries and the Department of Europe and North America, remained soft and Aerospace Engineering (DIAS) of the University customer confidence in making purchase of Naples "Federico II" are deeply involved in decision in these regions remained weak. This the design of a new commuter aircraft that inactivity, nonetheless, was offset in part by should be introduced in this market with very demand from the emerging markets of China good opportunities of success. This paper aims and Russia. While a full resurgence did not take to provide some guidelines on the conception of place in 2011, the year finished with signs of a new twin-engine commuter aircraft with recovery and reason of optimism. GAMA eleven passengers. Aircraft configuration and (General Aviation Manufacturer Association) cabin layouts choices are shown, also compared 2011 Statistical Databook & Industry Outlook to the main competitors.
    [Show full text]
  • Aircraft Library 
    Interagency Aviation Training Aircraft Library Disclaimer: The information provided in the Aircraft Library is intended to provide basic information for mission planning purposes and should NOT be used for flight planning. Due to variances in Make and Model, along with aircraft configuration and performance variability, it is necessary acquire the specific technical information for an aircraft from the operator when planning a flight. Revised: June 2021 Interagency Aviation Training—Aircraft Library This document includes information on Fixed-Wing aircraft (small, large, air tankers) and Rotor-Wing aircraft/Helicopters (Type 1, 2, 3) to assist in aviation mission planning. Click on any Make/Model listed in the different categories to view information about that aircraft. Fixed-Wing Aircraft - SMALL Make /Model High Low Single Multi Fleet Vendor Passenger Wing Wing engine engine seats Aero Commander XX XX XX 5 500 / 680 FL Aero Commander XX XX XX 7 680V / 690 American Champion X XX XX 1 8GCBC Scout American Rockwell XX XX 0 OV-10 Bronco Aviat A1 Husky XX XX X XX 1 Beechcraft A36/A36TC XX XX XX 6 B36TC Bonanza Beechcraft C99 XX XX XX 19 Beechcraft XX XX XX 7 90/100 King Air Beechcraft 200 XX XX XX XX 7 Super King Air Britten-Norman X X X 9 BN-2 Islander Cessna 172 XX XX XX 3 Skyhawk Cessna 180 XX XX XX 3 Skywagon Cessna 182 XX XX XX XX 3 Skylane Cessna 185 XX XX XX XX 4 Skywagon Cessna 205/206 XX XX XX XX 5 Stationair Cessna 207 Skywagon/ XX XX XX 6 Stationair Cessna/Texron XX XX XX 7 - 10 208 Caravan Cessna 210 X X x 5 Centurion Fixed-Wing Aircraft - SMALL—cont’d.
    [Show full text]
  • July2020.Pdf
    The JULY 2020 TWIN CESSNA Flyer FEATURING: THORNTON 310 - Youtube “310 PILOT” INTERIOR RENOVATIONS - PT. 1 FLY LIKE A PRO - TEN TIPS READERS WRITE SupportingSupporting Twin Twin Cessna Cessna Owners Owners Worldwide Worldwide since since 1988 1988 The AdvantageBetter Parts • Better Engines Cessna • Beechcraft • Cirrus Cessna: T206 TSIO-520-M P210 TSIO-520-P, -AF Beechcraft Bonanza: T210 TSIO-520-R 414A TSIO-520-NB 421B GTSIO-520-H F33, A36 IO-520-BB 310R IO-520-MB A36 IO-550-B T310 TSIO-520-BB, EB 421C GTSIO-520-L, -N Stock & Turbo-Normalized T310 TSIO-520-NB A36TC TSIO-520-UB 320 TSIO-520-EB, -NB Beechcraft Baron: B36TC TSIO-520-UB 335 TSIO-520-EB 58 IO-520-CB 340/A TSIO-520-NB 58 IO-550-C Cirrus: 402 B/C TSIO-520-EB/-VB 58 P/ TC TSIO-520-LB SR22 IO-550-N 404 GTSIO-520-M 58 P/ TC TSIO-520-WB Stock & Turbo-Normalized 414 TSIO-520-NB Critical Gears In Stock! NEW Crankcases for: RAM PMA-New gears are back in stock. If you are overhauling an • Beechcraft Baron • Cessna T310 engine (of having someone overhaul yours), contact RAM to get (58, 58P/TC) • Cessna 320 the best parts for your engine at a fraction of the OEM price! • Beechcraft Bonanza • Cessna 335 Large Cam Gear (C33A, E33A/C, F33, S35, • Cessna 340/A Replaces OEM #: 656818, V35/A/B, A36, A36TC, B36TC) • Cessna 402B/C 656031, 655516, 631845 • Cessna 310R • Cessna 414 RAM PN: 2078-1 • Cessna 414A Dealer Price: $850 • Cirrus SR22 Cost-Effective relief from Continental Critical Service Bulletin CSB05-8D Large Crankshaft Gear Replaces OEM #: 656991, 632893 RAM PN: 2074-1 Dealer Price: $896 Small Crankshaft Gear Replaces OEM #: 657175, 656989, 653652, 632892, 629301 RAM PN: 2075-11 AIRCRAFT PARTS STORE Dealer Price: $395 • SINCE 1976 • RAM AIRCRAFT, LP • SINCE 1976 • ©2020 RAM Aircraft, LP TTCF052720 The SM TWIN CESSNA Flyer FEATURES sm The Twin Cessna Flyer Wolter, owner of Air Mod Inc., one of the P.O.
    [Show full text]
  • Business & Commercial Aviation
    JUNE/JULY 2020 $10.00 AviationWeek.com/BCA Business & Commercial Aviation 2020 PURCHASE PLANNING HANDBOOK Production Aircraft Comparison A Look at the Trends and New AND Performance Tables Developments in Avionics ALSO IN THIS ISSUE Bombardier Global 7500 Smoke Signals Under Pressure Mountain Wave Monsters One Too Many Digital Edition Copyright Notice The content contained in this digital edition (“Digital Material”), as well as its selection and arrangement, is owned by Informa. and its affiliated companies, licensors, and suppliers, and is protected by their respective copyright, trademark and other proprietary rights. Upon payment of the subscription price, if applicable, you are hereby authorized to view, download, copy, and print Digital Material solely for your own personal, non-commercial use, provided that by doing any of the foregoing, you acknowledge that (i) you do not and will not acquire any ownership rights of any kind in the Digital Material or any portion thereof, (ii) you must preserve all copyright and other proprietary notices included in any downloaded Digital Material, and (iii) you must comply in all respects with the use restrictions set forth below and in the Informa Privacy Policy and the Informa Terms of Use (the “Use Restrictions”), each of which is hereby incorporated by reference. Any use not in accordance with, and any failure to comply fully with, the Use Restrictions is expressly prohibited by law, and may result in severe civil and criminal penalties. Violators will be prosecuted to the maximum possible extent. You may not modify, publish, license, transmit (including by way of email, facsimile or other electronic means), transfer, sell, reproduce (including by copying or posting on any network computer), create derivative works from, display, store, or in any way exploit, broadcast, disseminate or distribute, in any format or media of any kind, any of the Digital Material, in whole or in part, without the express prior written consent of Informa.
    [Show full text]
  • THE INCOMPLETE GUIDE to AIRFOIL USAGE David Lednicer
    THE INCOMPLETE GUIDE TO AIRFOIL USAGE David Lednicer Analytical Methods, Inc. 2133 152nd Ave NE Redmond, WA 98052 [email protected] Conventional Aircraft: Wing Root Airfoil Wing Tip Airfoil 3Xtrim 3X47 Ultra TsAGI R-3 (15.5%) TsAGI R-3 (15.5%) 3Xtrim 3X55 Trener TsAGI R-3 (15.5%) TsAGI R-3 (15.5%) AA 65-2 Canario Clark Y Clark Y AAA Vision NACA 63A415 NACA 63A415 AAI AA-2 Mamba NACA 4412 NACA 4412 AAI RQ-2 Pioneer NACA 4415 NACA 4415 AAI Shadow 200 NACA 4415 NACA 4415 AAI Shadow 400 NACA 4415 ? NACA 4415 ? AAMSA Quail Commander Clark Y Clark Y AAMSA Sparrow Commander Clark Y Clark Y Abaris Golden Arrow NACA 65-215 NACA 65-215 ABC Robin RAF-34 RAF-34 Abe Midget V Goettingen 387 Goettingen 387 Abe Mizet II Goettingen 387 Goettingen 387 Abrams Explorer NACA 23018 NACA 23009 Ace Baby Ace Clark Y mod Clark Y mod Ackland Legend Viken GTO Viken GTO Adam Aircraft A500 NASA LS(1)-0417 NASA LS(1)-0417 Adam Aircraft A700 NASA LS(1)-0417 NASA LS(1)-0417 Addyman S.T.G. Goettingen 436 Goettingen 436 AER Pegaso M 100S NACA 63-618 NACA 63-615 mod AerItalia G222 (C-27) NACA 64A315.2 ? NACA 64A315.2 ? AerItalia/AerMacchi/Embraer AMX ? 12% ? 12% AerMacchi AM-3 NACA 23016 NACA 4412 AerMacchi MB.308 NACA 230?? NACA 230?? AerMacchi MB.314 NACA 230?? NACA 230?? AerMacchi MB.320 NACA 230?? NACA 230?? AerMacchi MB.326 NACA 64A114 NACA 64A212 AerMacchi MB.336 NACA 64A114 NACA 64A212 AerMacchi MB.339 NACA 64A114 NACA 64A212 AerMacchi MC.200 Saetta NACA 23018 NACA 23009 AerMacchi MC.201 NACA 23018 NACA 23009 AerMacchi MC.202 Folgore NACA 23018 NACA 23009 AerMacchi
    [Show full text]
  • Legacy Vs. Late Model Flying for a Cause: Part 2 Dutch Treat: Flying to “Deadliest Catch” Port Radome TLC
    FOR THE PILOTS OF OWNER-FLOWN, CABIN-CLASS AIRCRAFT MAY 2017 $3.95 US VOLUME 21 NUMBER 5 When Picking Your First Jet Legacy vs. Late Model Flying For a Cause: Part 2 Dutch Treat: Flying to “Deadliest Catch” Port Radome TLC May 2017 CJ FAMILY INNOVATION. PERFORMA N C E . LEADERSHIP. CJ3+ CJ4 M2 Textron Aviation Full Page 4/C Ad GO WHERE YOUR VISION TAKES YOUwww.cessna.com There’s a smarter way to move y our business and your family. From Chicago to Key Largo or anyw here between, the Cessna Citation CJ F amily delivers time-saving mobility and access to t housands of sm all airports. All three aircraft have a common type rating, making it easier and more ecient than ever to grow with your business. Learn more at Cessna.com. U.S. +1.844. 44.TXTAV | INTERNATIO NAL +1.316.517.8270 ©2017 Textron Aviatio n Inc. All rights reserved. Cessna & Design , Citation, M2, CJ3 and CJ4 ar e trademarks or service marks of Textron Aviation Inc. o r a n a liate and may be registered in th e United States. 2 • TWIN & TURBINE May 2017 2 Editor’s Briefing by Dianne White May 2017 • VOL. 21, NO. 5 4 Legally Speaking Contents The Dreaded 709 Re-Examination by Jerry H. Trachtman Jet Journal 6 Legacy vs. Late Model Which One Makes Sense? 6 by Dianne White 7 Why I Love My Legacy Citation by Howard Tobin 10 Why I Love My Mustang by Ken Fielding 14 Flying For a Cause Part 2: The “How” of Charitable Flying 14 by Joe Ratterman 20 Dutch Treat A Visit to "Deadliest Catch" Port by Kevin Ware 26 Five on the Fly 20 by Rebecca Groom Jacobs 28 Tax Talk: Partners in Flight by Phil Crowther 32 Winning the Demo Flight by Rebecca Groom Jacobs Twin Proficiency 26 36 A Decision of Convenience by Thomas P.
    [Show full text]
  • STC / TC KITS CONVERSION CATALOG Mccauley PROPELLERS for YOUR GRAND CARAVAN
    STC / TC KITS CONVERSION CATALOG McCAULEY PROPELLERS FOR YOUR GRAND CARAVAN STC / TC KITS CONVERSION CATALOG [email protected] | 316.831.4021 | WWW.MCCAULEY.TEXTRON.COM Table of Contents Aircraft Manufacturer/Type Beechcraft Jetstream Single-Engine Piston Turboprop Twin-Engine Piston Turboprop Maule Single-Engine Piston Bellanca Single-Engine Piston Micco Single-Engine Piston Cessna Single-Engine Piston Mooney Twin-Engine Piston Single-Engine Piston Turboprop Spinner Kits Navion Single-Engine Piston Cirrus Single-Engine Piston Piper Single-Engine Piston De Havilland Twin-Engine Piston Turboprop Turboprop Grumman Socata Twin-Engine Piston Single-Engine Piston McCauley Propeller Systems 9709 E Central Wichita, KS 67206 (800) 621-7767 (316) 831-4021 www.mccauley.textron.com McCauley Conversion Abbreviation Guide PL-12345 — McCauley STC kit* PL — STC kit 12345 — Kit number BAR512-01PAC — McCauley TC kit** BAR — Relates to the application (BAR = Beech Baron models, CES = Cessna multiple models, 206 = Cessna 206 models, MLE = Maule multiple models, etc.) 512-01 — Abbreviated propeller assembly number (e.g., P5125358-01) P — Polished spinner assembly (if not present, indicates non-polished spinner assembly to be painted by customer) AC — Eligible for installation on aircraft with air-conditioning installed 180203-57-1 – McCauley TC kit** 180 — Cessna 180 models 203-57 — Abbreviated propeller assembly number (e.g., P2033909-57) -1 — Denotes variation with kit contents and/or eligibility (e.g., kits 180203-57-1 and 180203-57-2 contain the same P2033909-57 propeller, but a different spinner assembly is included due to eligibility for different 180 series aircraft) Determining if a kit is provided with or without icing protection.
    [Show full text]
  • 201409 General Aviation Report September 2014
    OCCURRENCE LISTING Aircraft Below 5700kg OCCURRENCES RECORDED BETWEEN 01 September 2014 and 30 September 2014 FIXED WING AIRCRAFT AERO AT3 BOMBARDIER ROTAX Climb to cruising POL 09/08/2014 201410835 level or altitude Infringement of Airway N57A (Class A) by an AT3. Standard separation maintained. I was alerted by CAIT to an infringer West of POL on a EGNH 0450 conspicuity code. I contacted EGNH and they transmitted to the aircraft and he confirmed he was passing 8300ft (base 4500ft), I instructed EGNH to inform the aircraft to descend and turn West immediately, due pending EGNM departures. The aircraft continued to track East and started to descend. A EGNM departure was given a HDG of 180deg to keep clear. The highest observed level of the aircraft was FL86. AMERICAN GENERAL AG5 LYCOMING Cruise 52 58N 02 32W 17/08/2014 201411281 360 FAMILY Infringement of the Daventry CTA (Class A) by an AG5B at FL70. Standard separation maintained. A CAIT return was seen at position 52 58N 02 32W at FL70. No ID was determined from Mode S. The next controller told me the aircraft went to Sleap. Supplementary 27/08/14: The pilot considers that the incident occurred whilst he was avoiding weather/cloud. AVID BOMBARDIER ROTAX En-route Midhurst 13/09/2014 201412938 582 UK Reportable Accident: Aircraft suffered engine failure and made forced landing in a field. One POB, no injuries reported. Subject to AAIB AARF investigation. AVIONS ROBIN DR400 LYCOMING Cruise EGGW (LTN): 16/08/2014 201411332 235 FAMILY London/Luton Infringement of the Luton CTA (Class D) by a DR400 at 3800ft.
    [Show full text]
  • Cessna's Versatile 402 Twin
    FOR THE PILOTS OF OWNER-FLOWN, CABIN-CLASS AIRCRAFT OCTOBER 2015 $3.95 US VOLUME 19 NUMBER 10 Cessna’s Versatile 402 Twin Airspeed, Alpha & Attitude Don’t Drive On The Greens Do We Need A Medical? Quest Aircraft Full Page 4/C Ad 2 • TWIN & TURBINE OCTOBER 2015 Quest Aircraft Full Page 4/C Ad OCTOBER 2015 TWIN & TURBINE • 1 L-3 Communications Full Page 4/C Ad 2 • TWIN & TURBINE OCTOBER 2015 Contents OCTOBER 2015 • VOL. 19, NO. 10 EDITOR FEATURES LeRoy Cook 4 Editorial EDITORIAL OFFICE 2779 Aero Park Drive Do We Need A Third Class Medical? Traverse City, MI 49686 Phone: (660) 679-5650 E-mail: [email protected] 6 The Cessna 402 PUBLISHERS J. Scott Lizenby A Versatile Cabin-Class Twin Dave Moore 6 PRESIDENT Twin Proficiency Dave Moore 16 Confident Go II: CFO J. Scott Lizenby Don’t Drive On The Greens PRODUCTION MANAGER Thomas Turner Mike Revard PUBLICATIONS DIRECTOR Steve Smith 22 The Gray Area GRAPHIC DESIGN Are You Current, Proficient, or Both? 16 Michael McCatty Todd Hotes ADVERTISING DIRECTOR John Shoemaker Twin & Turbine Airspeed, Alpha and Attitude 2779 Aero Park Drive 24 Traverse City, MI 49686 The Basics of Flying Phone: 1-800-773-7798 Fax: (231) 946-9588 [email protected] From The Flight Deck REPRINT SALES DIRECTOR 22 MEDIA COORDINATOR 28 Old-School ADVERTISING ADMINISTRATIVE ASSISTANT Kevin R. Dingman Betsy Beaudoin Phone: 1-800-773-7798 [email protected] 31 En Route: SUBSCRIBER SERVICES Pacific Coast Avionics Upgrades Meridian Rhonda Kelly San Juana Fisher FlightSafety Adding King Air 350 Simulator Diane Chauvin Quest Aircraft Expands P.O.
    [Show full text]
  • TMB 2017 Noise Contours
    | TABLE OF CONTENTS TMB 2017 Noise Contours Page Sections 1.0 Introduction and Overview 1 2.0 TMB ANOMS Aircraft Operations 1 3.0 Aircraft Fleet Mix 2 4.0 Stage Lengths 2 5.0 Time of Day 3 6.0 Runway Use 3 7.0 Flight Track and Flight Track Use Percentages 5 8.0 2017 DNL Noise Contours 13 9.0 2009 versus 2017 DNL Noise Contour Comparison 13 Appendices A Operations Information List of Figures Figure 1: Fixed-Wing AEDT Flight Tracks – East Flow Figure 2: Fixed-Wing AEDT Flight Tracks – West Flow Figure 3: Helicopter and Fixed-Wing Touch-and-Go AEDT Flight Tracks Figure 4: 2017 DNL Contours Figure 5: 2017 and 2009 DNL Contour Comparison Figure 6: Differences in Noise Exposure – 2009 versus 2017 DNL Contours List of Tables Table 1: 2017 Daytime and Nighttime Use Percentages 3 Table 2: 2017 Runway Use Percentages – Fixed-Wing Aircraft 4 Table 3: 2017 Runway Use Percentages – Helicopter Touch-and-Go Operations 4 Table 4: 2017 DNL Contour Areas 13 Table 5: DNL Contour Area Comparison 14 Table 6: Aircraft Operations Comparison with Nighttime-Weighted Operations 14 Table 7: Overall Runway Use Comparison 15 Miami Executive Airport i ESA / Project No. 170069.02 2017 Noise Contours December 2018 Table of Contents This Page Intentionally Blank Miami Executive Airport ii ESA / Project No. 170069.02 2017 Noise Contours December 2018 MIAMI EXECUTIVE AIRPORT 2017 Noise Contours 1.0 Introduction and Overview This report provides an analysis and overview of the noise modeling data preparation and resulting contours for the calendar year 2017 at Miami Executive Airport (TMB).
    [Show full text]