Who Can Name the Bigger Number?
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Busy Beaver Frontier
Electronic Colloquium on Computational Complexity, Report No. 115 (2020) The Busy Beaver Frontier Scott Aaronson∗ Abstract The Busy Beaver function, with its incomprehensibly rapid growth, has captivated genera- tions of computer scientists, mathematicians, and hobbyists. In this survey, I offer a personal view of the BB function 58 years after its introduction, emphasizing lesser-known insights, re- cent progress, and especially favorite open problems. Examples of such problems include: when does the BB function first exceed the Ackermann function? Is the value of BB(20) independent of set theory? Can we prove that BB(n + 1) > 2BB(n) for large enough n? Given BB(n), how many advice bits are needed to compute BB(n + 1)? Do all Busy Beavers halt on all inputs, not just the 0 input? Is it decidable, given n, whether BB(n) is even or odd? 1 Introduction The Busy Beaver1 function, defined by Tibor Rad´o[13] in 1962, is an extremely rapidly-growing function, defined by maximizing over the running times of all n-state Turing machines that eventu- ally halt. In my opinion, the BB function makes the concepts of computability and uncomputability more vivid than anything else ever invented. When I recently taught my 7-year-old daughter Lily about computability, I did so almost entirely through the lens of the ancient quest to name the biggest numbers one can. Crucially, that childlike goal, if pursued doggedly enough, inevitably leads to something like the BB function, and hence to abstract reasoning about the space of possi- ble computer programs, the halting problem, and so on.2 Let's give a more careful definition. -

Grade 7/8 Math Circles the Scale of Numbers Introduction
Faculty of Mathematics Centre for Education in Waterloo, Ontario N2L 3G1 Mathematics and Computing Grade 7/8 Math Circles November 21/22/23, 2017 The Scale of Numbers Introduction Last week we quickly took a look at scientific notation, which is one way we can write down really big numbers. We can also use scientific notation to write very small numbers. 1 × 103 = 1; 000 1 × 102 = 100 1 × 101 = 10 1 × 100 = 1 1 × 10−1 = 0:1 1 × 10−2 = 0:01 1 × 10−3 = 0:001 As you can see above, every time the value of the exponent decreases, the number gets smaller by a factor of 10. This pattern continues even into negative exponent values! Another way of picturing negative exponents is as a division by a positive exponent. 1 10−6 = = 0:000001 106 In this lesson we will be looking at some famous, interesting, or important small numbers, and begin slowly working our way up to the biggest numbers ever used in mathematics! Obviously we can come up with any arbitrary number that is either extremely small or extremely large, but the purpose of this lesson is to only look at numbers with some kind of mathematical or scientific significance. 1 Extremely Small Numbers 1. Zero • Zero or `0' is the number that represents nothingness. It is the number with the smallest magnitude. • Zero only began being used as a number around the year 500. Before this, ancient mathematicians struggled with the concept of `nothing' being `something'. 2. Planck's Constant This is the smallest number that we will be looking at today other than zero. -

The Busy Beaver Competition: a Historical Survey Pascal Michel
The Busy Beaver Competition: a historical survey Pascal Michel To cite this version: Pascal Michel. The Busy Beaver Competition: a historical survey. 2017. hal-00396880v6 HAL Id: hal-00396880 https://hal.archives-ouvertes.fr/hal-00396880v6 Preprint submitted on 4 Sep 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. The Busy Beaver Competition: a historical survey Pascal MICHEL∗ Equipe´ de Logique Math´ematique, Institut de Math´ematiques de Jussieu–Paris Rive Gauche, UMR 7586, Bˆatiment Sophie Germain, case 7012, 75205 Paris Cedex 13, France and Universit´ede Cergy-Pontoise, ESPE, F-95000 Cergy-Pontoise, France [email protected] Version 6 September 4, 2019 Abstract Tibor Rado defined the Busy Beaver Competition in 1962. He used Turing machines to give explicit definitions for some functions that are not computable and grow faster than any computable function. He put forward the problem of computing the values of these functions on numbers 1, 2, 3, . .. More and more powerful computers have made possible the computation of lower bounds for these values. In 1988, Brady extended the definitions to functions on two variables. We give a historical survey of these works. -
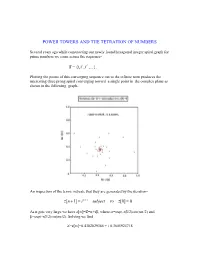
Power Towers and the Tetration of Numbers
POWER TOWERS AND THE TETRATION OF NUMBERS Several years ago while constructing our newly found hexagonal integer spiral graph for prime numbers we came across the sequence- i S {i,i i ,i i ,...}, Plotting the points of this converging sequence out to the infinite term produces the interesting three prong spiral converging toward a single point in the complex plane as shown in the following graph- An inspection of the terms indicate that they are generated by the iteration- z[n 1] i z[n] subject to z[0] 0 As n gets very large we have z[]=Z=+i, where =exp(-/2)cos(/2) and =exp(-/2)sin(/2). Solving we find – Z=z[]=0.4382829366 + i 0.3605924718 It is the purpose of the present article to generalize the above result to any complex number z=a+ib by looking at the general iterative form- z[n+1]=(a+ib)z[n] subject to z[0]=1 Here N=a+ib with a and b being real numbers which are not necessarily integers. Such an iteration represents essentially a tetration of the number N. That is, its value up through the nth iteration, produces the power tower- Z Z n Z Z Z with n-1 zs in the exponents Thus- 22 4 2 22 216 65536 Note that the evaluation of the powers is from the top down and so is not equivalent to the bottom up operation 44=256. Also it is clear that the sequence {1 2,2 2,3 2,4 2,...}diverges very rapidly unlike the earlier case {1i,2 i,3i,4i,...} which clearly converges. -

Attributes of Infinity
International Journal of Applied Physics and Mathematics Attributes of Infinity Kiamran Radjabli* Utilicast, La Jolla, California, USA. * Corresponding author. Email: [email protected] Manuscript submitted May 15, 2016; accepted October 14, 2016. doi: 10.17706/ijapm.2017.7.1.42-48 Abstract: The concept of infinity is analyzed with an objective to establish different infinity levels. It is proposed to distinguish layers of infinity using the diverging functions and series, which transform finite numbers to infinite domain. Hyper-operations of iterated exponentiation establish major orders of infinity. It is proposed to characterize the infinity by three attributes: order, class, and analytic value. In the first order of infinity, the infinity class is assessed based on the “analytic convergence” of the Riemann zeta function. Arithmetic operations in infinity are introduced and the results of the operations are associated with the infinity attributes. Key words: Infinity, class, order, surreal numbers, divergence, zeta function, hyperpower function, tetration, pentation. 1. Introduction Traditionally, the abstract concept of infinity has been used to generically designate any extremely large result that cannot be measured or determined. However, modern mathematics attempts to introduce new concepts to address the properties of infinite numbers and operations with infinities. The system of hyperreal numbers [1], [2] is one of the approaches to define infinite and infinitesimal quantities. The hyperreals (a.k.a. nonstandard reals) *R, are an extension of the real numbers R that contains numbers greater than anything of the form 1 + 1 + … + 1, which is infinite number, and its reciprocal is infinitesimal. Also, the set theory expands the concept of infinity with introduction of various orders of infinity using ordinal numbers. -

The Notion Of" Unimaginable Numbers" in Computational Number Theory
Beyond Knuth’s notation for “Unimaginable Numbers” within computational number theory Antonino Leonardis1 - Gianfranco d’Atri2 - Fabio Caldarola3 1 Department of Mathematics and Computer Science, University of Calabria Arcavacata di Rende, Italy e-mail: [email protected] 2 Department of Mathematics and Computer Science, University of Calabria Arcavacata di Rende, Italy 3 Department of Mathematics and Computer Science, University of Calabria Arcavacata di Rende, Italy e-mail: [email protected] Abstract Literature considers under the name unimaginable numbers any positive in- teger going beyond any physical application, with this being more of a vague description of what we are talking about rather than an actual mathemati- cal definition (it is indeed used in many sources without a proper definition). This simply means that research in this topic must always consider shortened representations, usually involving recursion, to even being able to describe such numbers. One of the most known methodologies to conceive such numbers is using hyper-operations, that is a sequence of binary functions defined recursively starting from the usual chain: addition - multiplication - exponentiation. arXiv:1901.05372v2 [cs.LO] 12 Mar 2019 The most important notations to represent such hyper-operations have been considered by Knuth, Goodstein, Ackermann and Conway as described in this work’s introduction. Within this work we will give an axiomatic setup for this topic, and then try to find on one hand other ways to represent unimaginable numbers, as well as on the other hand applications to computer science, where the algorith- mic nature of representations and the increased computation capabilities of 1 computers give the perfect field to develop further the topic, exploring some possibilities to effectively operate with such big numbers. -

Handout 2: October 25 Three Proofs of Undecidability Of
COS 487: Theory of Computation Fall 2000 Handout 2: October 25 Sanjeev Arora Three proofs of Undecidability of ATM (From G. Chaitin, “G¨o del’s Theorem and Information” International J. Theor. Physics 22 (1982), pp. 941-954.) 1. Define a function F where F (N) is defined to be either 1 more than the value of the Nth computable function applied to the natural number N, or zero if this value is undefined because the Nth computer program does not halt on input N. F cannot be a computable function, for if program M calculated it, then one would have F (M)= F (M) + 1, which is impossible. But the only way that F can fail to be computable is because one cannot decide in general if the Nth program ever halts when given input N. 2. This proof runs along the lines of Bertrand Russell’s paradox of the set of all things that are not members of themselves. Consider programs for enumerating sets of natural numbers, and number these computer programs. Define a set of natural numbers consisting of the numbers of all programs which do not include their own number in their output set. This set of natural numbers cannot be recursively enumerable, for if it were listed by computer program N, one arrives at Russell’s paradox of the barber in a small town who shaves all those and only those who do not shave themselves, and can neither shave himself nor avoid doing so. But the only way that this set can fail to be recursively enumerable is if it is impossible to decide whether or not a program ever outputs a specific natural number, and this is a variant of the halting problem. -

Hyperoperations and Nopt Structures
Hyperoperations and Nopt Structures Alister Wilson Abstract (Beta version) The concept of formal power towers by analogy to formal power series is introduced. Bracketing patterns for combining hyperoperations are pictured. Nopt structures are introduced by reference to Nept structures. Briefly speaking, Nept structures are a notation that help picturing the seed(m)-Ackermann number sequence by reference to exponential function and multitudinous nestings thereof. A systematic structure is observed and described. Keywords: Large numbers, formal power towers, Nopt structures. 1 Contents i Acknowledgements 3 ii List of Figures and Tables 3 I Introduction 4 II Philosophical Considerations 5 III Bracketing patterns and hyperoperations 8 3.1 Some Examples 8 3.2 Top-down versus bottom-up 9 3.3 Bracketing patterns and binary operations 10 3.4 Bracketing patterns with exponentiation and tetration 12 3.5 Bracketing and 4 consecutive hyperoperations 15 3.6 A quick look at the start of the Grzegorczyk hierarchy 17 3.7 Reconsidering top-down and bottom-up 18 IV Nopt Structures 20 4.1 Introduction to Nept and Nopt structures 20 4.2 Defining Nopts from Nepts 21 4.3 Seed Values: “n” and “theta ) n” 24 4.4 A method for generating Nopt structures 25 4.5 Magnitude inequalities inside Nopt structures 32 V Applying Nopt Structures 33 5.1 The gi-sequence and g-subscript towers 33 5.2 Nopt structures and Conway chained arrows 35 VI Glossary 39 VII Further Reading and Weblinks 42 2 i Acknowledgements I’d like to express my gratitude to Wikipedia for supplying an enormous range of high quality mathematics articles. -

Problems in Number Theory from Busy Beaver Competition
Logical Methods in Computer Science Vol. 11(4:10)2015, pp. 1–35 Submitted Mar. 11, 2015 www.lmcs-online.org Published Dec. 14, 2015 PROBLEMS IN NUMBER THEORY FROM BUSY BEAVER COMPETITION PASCAL MICHEL Equipe´ de Logique Math´ematique, Institut de Math´ematiques de Jussieu–Paris Rive Gauche, UMR 7586, Bˆatiment Sophie Germain, case 7012, 75205 Paris Cedex 13, France and Universit´ede Cergy- Pontoise, IUFM, F-95000 Cergy-Pontoise, France e-mail address: [email protected] Abstract. By introducing the busy beaver competition of Turing machines, in 1962, Rado defined noncomputable functions on positive integers. The study of these functions and variants leads to many mathematical challenges. This article takes up the following one: How can a small Turing machine manage to produce very big numbers? It provides the following answer: mostly by simulating Collatz-like functions, that are generalizations of the famous 3x+1 function. These functions, like the 3x+1 function, lead to new unsolved problems in number theory. 1. Introduction 1.1. A well defined noncomputable function. It is easy to define a noncomputable function on nonnegative integers. Indeed, given a programming language, you produce a systematic list of the programs for functions, and, by diagonalization, you define a function whose output, on input n, is different from the output of the nth program. This simple definition raises many problems: Which programming language? How to list the programs? How to choose the output? In 1962, Rado [Ra62] gave a practical solution by defining the busy beaver game, also called now the busy beaver competition. -

Mathematical Constants and Sequences
Mathematical Constants and Sequences a selection compiled by Stanislav Sýkora, Extra Byte, Castano Primo, Italy. Stan's Library, ISSN 2421-1230, Vol.II. First release March 31, 2008. Permalink via DOI: 10.3247/SL2Math08.001 This page is dedicated to my late math teacher Jaroslav Bayer who, back in 1955-8, kindled my passion for Mathematics. Math BOOKS | SI Units | SI Dimensions PHYSICS Constants (on a separate page) Mathematics LINKS | Stan's Library | Stan's HUB This is a constant-at-a-glance list. You can also download a PDF version for off-line use. But keep coming back, the list is growing! When a value is followed by #t, it should be a proven transcendental number (but I only did my best to find out, which need not suffice). Bold dots after a value are a link to the ••• OEIS ••• database. This website does not use any cookies, nor does it collect any information about its visitors (not even anonymous statistics). However, we decline any legal liability for typos, editing errors, and for the content of linked-to external web pages. Basic math constants Binary sequences Constants of number-theory functions More constants useful in Sciences Derived from the basic ones Combinatorial numbers, including Riemann zeta ζ(s) Planck's radiation law ... from 0 and 1 Binomial coefficients Dirichlet eta η(s) Functions sinc(z) and hsinc(z) ... from i Lah numbers Dedekind eta η(τ) Functions sinc(n,x) ... from 1 and i Stirling numbers Constants related to functions in C Ideal gas statistics ... from π Enumerations on sets Exponential exp Peak functions (spectral) .. -

Reihenalgebra: What Comes Beyond Exponentiation? M
Reihenalgebra: What comes beyond exponentiation? M. M¨uller, [email protected] Abstract Addition, multiplication and exponentiation are classical oper- ations, successively defined by iteration. Continuing the iteration process, one gets an infinite hierarchy of higher-order operations, the first one sometimes called tetration a... aa a b = a b terms , ↑ o followed by pentation, hexation, etc. This paper gives a survey on some ideas, definitions and methods that the author has developed as a young pupil for the German Jugend forscht science fair. It is meant to be a collection of ideas, rather than a serious formal paper. In particular, a definition for negative integer exponents b is given for all higher-order operations, and a method is proposed that gives a very natural (but non-trivial) interpolation to real (and even complex) integers b for pentation and hexation and many other operations. It is an open question if this method can also be applied to tetration. 1 Introduction Multiplication of natural numbers is nothing but repeated addition, a + a + a + ... + a = a b . (1) · b terms | {z } Iterating multiplication, one gets another operation, namely exponentiation: b a a a ... a = a =: aˆb . (2) · · · · b terms | {z } Classically, this is it, and one stops here. But what if one continues the iteration process? One could define something like aˆaˆaˆ ... ˆa = a b . ↑ b terms | {z } But, wait a minute, in contrast to eq. (1) and (6), this definition will depend on the way we set brackets, i.e. on the order of exponentiation! Thus, we have to distinguish between the two canonical possibilities aaa.. -

The Strange Properties of the Infinite Power Tower Arxiv:1908.05559V1
The strange properties of the infinite power tower An \investigative math" approach for young students Luca Moroni∗ (August 2019) Nevertheless, the fact is that there is nothing as dreamy and poetic, nothing as radical, subversive, and psychedelic, as mathematics. Paul Lockhart { \A Mathematician's Lament" Abstract In this article we investigate some "unexpected" properties of the \Infinite Power Tower 1" function (or \Tetration with infinite height"): . .. xx y = f(x) = xx where the \tower" of exponentiations has an infinite height. Apart from following an initial personal curiosity, the material collected here is also intended as a potential guide for teachers of high-school/undergraduate students interested in planning an activity of \investigative mathematics in the classroom", where the knowledge is gained through the active, creative and cooperative use of diversified mathematical tools (and some ingenuity). The activity should possibly be carried on with a laboratorial style, with no preclusions on the paths chosen and undertaken by the students and with little or no information imparted from the teacher's desk. The teacher should then act just as a guide and a facilitator. The infinite power tower proves to be particularly well suited to this kind of learning activity, as the student will have to face a challenging function defined through a rather uncommon infinite recursive process. They'll then have to find the right strategies to get around the trickiness of this function and achieve some concrete results, without the help of pre-defined procedures. The mathematical requisites to follow this path are: functions, properties of exponentials and logarithms, sequences, limits and derivatives.