Tides of NE and NY.Pdf
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Partial Class A-2 Response Action Outcome Statement
GeoInsight, Inc. GeoInsight, Inc. GeoInsight, Inc. 75 Gilcreast Road, Suite 210 319 Littleton Road, Suite 105 Corporate Ten Center Londonderry, NH 03053-3566 Westford, MA 01886 1781 Highland Avenue, Suite 207 TEL 603-434-3116 TEL 978-692-1114 Cheshire, CT 06410 FAX 603-432-2445 FAX 978-692-1115 TEL 203-271-8036 www.geoinsightinc.com FAX 203-271-8038 PARTIAL CLASS A-2 RESPONSE ACTION OUTCOME STATEMENT BARGE B120 SPILL BUZZARDS BAY, MASSACHUSETTS RTN 4-17786 Prepared For: Bouchard Transportation Company, Inc. 58 South Service Road, Suite 150 Melville, NY 11747 Prepared By: GeoInsight, Inc. 319 Littleton Road, Suite 105 Westford, Massachusetts 01886 Phone: (978) 692-1114 Fax: (978) 692-1115 www.geoinsightinc.com May 21, 2004 GeoInsight Project 3871-000 File: 3871 RAO FINAL Environmental Solutions at Work GeoInsight, INC. TABLE OF CONTENTS SECTION PAGE 1.0 INTRODUCTION..............................................................................................................1 2.0 RELEASE BACKGROUND.............................................................................................3 2.1 SEGMENT IDENTIFICATION....................................................................................4 2.2 SEGMENT RANKING AND GROUPING..................................................................5 3.0 SUMMARY OF RESPONSE ACTIONS ........................................................................7 3.1 UNIFIED COMMAND INITIAL RESPONSE ACTIONS ..........................................7 3.2 IRAC EVALUATION.................................................................................................10 -

Immediate Response Action Status Report Barge B120
GeoInsight, Inc. GeoInsight, Inc. GeoInsight, Inc. 75 Gilcreast Road, Suite 210 319 Littleton Road, Suite 105 Corporate Ten Center Londonderry, NH 03053-3566 Westford, MA 01886 1781 Highland Avenue, Suite 207 TEL 603-434-3116 TEL 978-692-1114 Cheshire, CT 06410 FAX 603-432-2445 FAX 978-692-1115 TEL 203-271-8036 www.geoinsightinc.com FAX 203-271-8038 IMMEDIATE RESPONSE ACTION STATUS REPORT BARGE B120 SPILL BUZZARDS BAY, MASSACHUSETTS RTN 4-17786 Prepared For: Bouchard Transportation Company, Inc. 58 South Service Road, Suite 150 Melville, NY 11747 Prepared By: GeoInsight, Inc. 319 Littleton Road, Suite 105 Westford, Massachusetts 01886 Phone: (978) 692-1114 Fax: (978) 692-1115 www.geoinsightinc.com September 16, 2004 Environmental Solutions at Work Massachusetts Department of Environmental Protection Bureau of Waste Site Cleanup BWSC105 Release Tracking Number IMMEDIATE RESPONSE ACTION (IRA) TRANSMITTAL FORM Pursuant to 310 CMR 40.0424 - 40.0427 (Subpart D) - A. RELEASE OR THREAT OF RELEASE LOCATION: 1. Release Name/Location Aid: 2. Street Address: 3. City/Town: 4. ZIP Code: 5. Check here if a Tier Classification Submittal has been provided to DEP for this Disposal Site. a. Tier 1A b. Tier 1B c. Tier 1C d. Tier 2 6. Check here if this location is Adequately Regulated, pursuant to 310 CMR 40.0110-0114. Specify Program (check one): a. CERCLA b. HSWA Corrective Action c. Solid Waste Management d. RCRA State Program (21C Facilities) B. THIS FORM IS BEING USED TO: (check all that apply) 1. List Submittal Date of Initial IRA Written Plan (if previously submitted): (MM/DD/YYYY) 2. -

LCSH Section E
E (The Japanese word) E♭ horn Lake Spence (Tex.) [PL669.E] USE Alto horn Spence Reservoir (Tex.) BT Japanese language—Etymology E Ingakyō (Scrolls) BT Lakes—Texas e (The number) UF Kako genzai ingakyō emaki (Scrolls) Reservoirs—Texas UF Napier number BT Painting, Japanese E.V. Wilkins Post Office (Roper, N.C.) Number, Napier Scrolls, Japanese UF Wilkins Post Office (Roper, N.C.) BT Logarithmic functions E-invoices BT Post office buildings—North Carolina Transcendental numbers USE Electronic invoices E-violin Ë (The Russian letter) E. J. Pugh (Fictitious character) USE Electric violin BT Russian language—Alphabet USE Pugh, E. J. (Fictitious character) E-voting E & E Ranch (Tex.) E.J. Thomas Performing Arts Hall (Akron, Ohio) USE Electronic voting UF E and E Ranch (Tex.) UF Edwin J. Thomas Performing Arts Hall (Akron, E-waste BT Ranches—Texas Ohio) USE Electronic waste E.326 (Electric locomotives) (Not Subd Geog) BT Centers for the performing arts—Ohio e World (Online service) BT Electric locomotives E-journals USE eWorld (Online service) E.428 (Electric locomotives) (Not Subd Geog) USE Electronic journals E. Y. Mullins Lectures on Preaching BT Electric locomotives E.L. Kirchner Haus (Frauenkirch, Switzerland) UF Mullins Lectures on Preaching E-605 (Insecticide) USE In den Lärchen (Frauenkirch, Switzerland) BT Preaching USE Parathion E. L. Pender (Fictitious character) E-zines (May Subd Geog) E.626 (Electric locomotives) (Not Subd Geog) USE Pender, Ed (Fictitious character) UF Ezines BT Electric locomotives E-lists (Electronic discussion groups) BT Electronic journals E.1027 (Roquebrune-Cap-Martin, France) USE Electronic discussion groups Zines UF E1027 (Roquebrune-Cap-Martin, France) E. -

Dukes County, Massachusetts (All Jurisdictions)
DUKES COUNTY, MASSACHUSETTS (ALL JURISDICTIONS) COMMUNITY NAME COMMUNITY NUMBER AQUINNAH, TOWN OF 250070 CHILMARK, TOWN OF 250068 EDGARTOWN, TOWN OF 250069 GOSNOLD, TOWN OF 250071 OAK BLUFFS, TOWN OF 250072 TISBURY, TOWN OF 250073 WEST TISBURY, TOWN OF 250074 Dukes County Federal Emergency Management Agency FLOOD INSURANCE STUDY NUMBER 25007CV000B NOTICE TO FLOOD INSURANCE STUDY USERS Communities participating in the National Flood Insurance Program have established repositories of flood hazard data for floodplain management and flood insurance purposes. This Flood Insurance Study (FIS) may not contain all data available within the repository. It is advisable to contact the community repository for any additional data. Selected Flood Insurance Rate Map panels for the community contain information that was previously shown separately on the corresponding Flood Boundary and Floodway Map panels (e.g., floodways, cross sections). In addition, former flood hazard zone designations have been changed as follows: Old Zone New Zone A1 through A30 AE V1 through V30 VE B X C X Part or all of this Flood Insurance Study may be revised and republished at any time. In addition, part of this Flood Insurance Study may be revised by the Letter of Map Revision process, which does not involve republication or redistribution of the Flood Insurance Study. It is, therefore, the responsibility of the user to consult with community officials and to check the community repository to obtain the most current Flood Insurance Study components. Initial Countywide FIS -

The Connecticut Ornithological Association 314 Unquowaroad Non-Profit Org
Winter 1990 Contents Volume X Number 1 January 1990 THE 1 A Tribute to Michael Harwood David A Titus CONNECTICUT 2 Site Guide Birder's Guide to the Mohawk State Forest and Vicinity Arnold Devine and Dwight G. Smith I WARBLER ~ A Journal of Connecticut Ornithology 10 Non-Breeding Bald Eagles in Northwest Con necticut During Late Spring and Summer D. A Hopkins 15 Notes on Birds Using Man-Made Nesting Materials William E. Davis, Jr. 19 Connecticut Field Notes Summer: June 1 -July 31, 1989 Jay Kaplan 24 Corrections The Connecticut Ornithological Association 314 UnquowaRoad Non-Profit Org. Fairfield, cr 06430 U.S. Postage PAID Fairfield, CT Permit No. 275 :.'• ~}' -'~~- .~ ( Volume X No. 1 January 1990 Pages 1-24 j ~ THE CONNECTICUf ORNITHOLOGICAL A TRIBUTE TO MICHAEL HARWOOD ASSOCIATION Michael Harwood (1934-1989) "I remember a lovely May morning in Central Park in New York. ... PreBident Debra M. Miller, Franklin, MA A friend and I heard an unfamiliar song, a string of thin, wiry notes Vice-President climbing the upper register in small steps; we traced it to a tiny yellow Frank Mantlik, S. Norwalk •, bird in a just-planted willow tree. To say that the bird was 'yellow' Secretary does not do it justice. Its undersides were the very essence of yellow, Alison Olivieri, Fairfield and this yellow was set off by the black stripes on the breast, by the Trea.urer •• dramatic triangle of black drawn on its yellow face, and by the Carl J. Trichka, Fairfield chestnut piping on its back, where the yellow turned olive .. -

Updated Conceptual Site Model Barge B120 Spill
GeoInsight, INC. UPDATED CONCEPTUAL SITE MODEL BARGE B120 SPILL BUZZARDS BAY, MASSACHUSETTS RTN 4-17786 Prepared For: Bouchard Transportation Company, Inc. 58 South Service Road, Suite 150 Melville, New York 11747 Prepared By: GeoInsight, Inc. 319 Littleton Road, Suite 105 Westford, Massachusetts 01886 Phone: (978) 692-1114 Fax: (978) 692-1115 www.geoinsightinc.com August 24, 2005 GeoInsight, INC. TABLE OF CONTENTS SECTION PAGE 1.0 INTRODUCTION............................................................................................................. 1 1.1 CONCEPTUAL SITE MODEL OBJECTIVES............................................................. 1 1.2 NUMERICAL MODELING OVERVIEW .................................................................... 2 1.3 LITERATURE OVERVIEW..........................................................................................2 1.4 FIELD OBSERVATIONS OVERVIEW ....................................................................... 2 1.5 INCIDENT OVERVIEW............................................................................................... 3 2.0 RELEASE INFORMATION ........................................................................................... 4 2.1 GENERAL PROPERTIES OF NO. 6 FUEL OIL.......................................................... 4 2.2 PROPERTIES OF THE B120 OIL................................................................................. 5 2.2.1 Physical Characteristics.......................................................................................... 5 2.2.2 -

Appendix III
Appendix III Sample pages from the Center for Operational Oceanographic Products and Services (CO-OPS) tidal prediction web site. Station name and location are listed along with the Mean Range, Spring Range, and Mean Tide Level. The “Predictions” links display the predicted tides (date, day, time, and height) for that location for each day for an entire year. From http://co- ops.nos.noaa.gov/tides03/tab2ec1b.html#8. 1 4/5/2005 Tidal Station Locations and Ranges MASSACHUSETTS, outer coast Mean Spring Mean Tide Range Range Level Station Latitude Longitude (ft) (ft) (ft) Predictions Merrimack River entrance 42° 49' 70° 49' 8.3 9.5 4.4 Predictions Newburyport, Merrimack River 42° 49' 70° 52' 7.8 9.0 4.2 Predictions Plum Island Sound (south end) 42° 43' 70° 47' 8.6 9.9 4.6 Predictions Annisquam 42° 39' 70° 41' 8.7 10.1 4.7 Predictions Rockport 42° 40' 70° 37' 8.6 10.0 4.6 Predictions Gloucester Harbor 42° 36' 70° 40' 8.7 10.1 4.6 Predictions Manchester Harbor 42° 34' 70° 47' 8.8 10.2 4.7 Predictions Beverly 42° 32' 70° 53' 9.0 10.4 4.8 Predictions Salem 42° 31' 70° 53' 8.8 10.2 4.7 Predictions Marblehead 42° 30' 70° 51' 9.1 10.6 4.8 Predictions Broad Sound Nahant 42° 25' 70° 55' 9.0 10.4 4.8 Predictions Lynn Harbor 42° 27' 70° 58' 9.2 10.7 4.9 Predictions Boston Harbor Mean Spring Mean Tide Range Range Level Station Latitude Longitude (ft) (ft) (ft) Predictions Boston Light 42° 20' 70° 53' 9.0 10.4 4.8 Predictions Lovell Island, The Narrows 42° 20' 70° 56' 9.1 10.6 4.8 Predictions Deer Island (south end) 42° 21' 70° 58' 9.3 10.8 4.9 Predictions Belle Isle Inlet entrance 42° 23' 71° 00' 9.5 11.0 5.0 Predictions Castle Island 42° 20' 71° 01' 9.4 10.9 5.0 Predictions BOSTON 42° 21' 71° 03' 9.5 11.0 5.1 Predictions Dover St. -
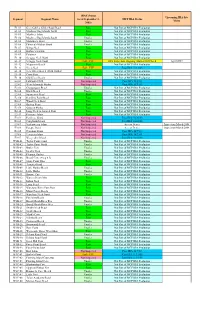
Shoreline Status 02-04
IRAC Status Upcoming IRA Site Segment Segment Name (as of September 3, MCP IRA Status Visits 2003) E1-01 Grey Gables-Gilder Road Beach Pass Not Part of MCP IRA Evaluation E1-02 Mashnee/Hog Islands North Pass Not Part of MCP IRA Evaluation E1-03 Mashnee Island Pass Not Part of MCP IRA Evaluation E1-04 Mashnee/Hog Islands South Unoiled Not Part of MCP IRA Evaluation E1-05 Monument Beach Unoiled Not Part of MCP IRA Evaluation E1-06 Phinney's Harbor South Unoiled Not Part of MCP IRA Evaluation E1-07 Wings Neck Pass Not Part of MCP IRA Evaluation E1-08 Barlow's Landing Pass Not Part of MCP IRA Evaluation E1-09 Patuisset Pass Not Part of MCP IRA Evaluation E1-10 Scraggy Neck North Pass Not Part of MCP IRA Evaluation E1-11 Scraggy Neck South Fail - FTF IRA Inspection Ongoing (Buried Oil Check April 2004 E1-12 Megansett Beach Pass Not Part of MCP IRA Evaluation E1-13 Nye's Neck Fail - FTF Pass IRA 11/11/03 E1-14 New Silver Beach (Wild Harbor) Pass Not Part of MCP IRA Evaluation E1-15 Crow Point Pass Not Part of MCP IRA Evaluation E1-16 Old Silver Beach Unoiled Not Part of MCP IRA Evaluation E2-01 Falmouth Cliffs Not Inspected Pass IRA 11/3/03 E2-02 West Falmouth Harbor Not Inspected Pass IRA 11/3/03 E2-03 Chappaquoit Beach Unoiled Not Part of MCP IRA Evaluation E2-04 Black Beach Unoiled Not Part of MCP IRA Evaluation E2-05 Saconesset Beach Pass Not Part of MCP IRA Evaluation E2-06 Hamlin's Point Beach Pass Not Part of MCP IRA Evaluation E2-07 Wood Neck Beach Pass Not Part of MCP IRA Evaluation E2-08 Racing Beach Pass Not Part of MCP IRA Evaluation -

LCSH Section U
U-2 (Reconnaissance aircraft) (Not Subd Geog) U.S. 29 U.S. Bank Stadium (Minneapolis, Minn.) [TL686.L (Manufacture)] USE United States Highway 29 BT Stadiums—Minnesota [UG1242.R4 (Military aeronautics)] U.S. 30 U.S. Bicycle Route System (May Subd Geog) UF Lockheed U-2 (Airplane) USE United States Highway 30 UF USBRS (U.S. Bicycle Route System) BT Lockheed aircraft U.S. 31 BT Bicycle trails—United States Reconnaissance aircraft USE United States Highway 31 U.S.-Canada Border Region U-2 (Training plane) U.S. 40 USE Canadian-American Border Region USE Polikarpov U-2 (Training plane) USE United States Highway 40 U.S. Capitol (Washington, D.C.) U-2 Incident, 1960 U.S. 41 USE United States Capitol (Washington, D.C.) BT Military intelligence USE United States Highway 41 U.S. Capitol Complex (Washington, D.C.) Military reconnaissance U.S. 44 USE United States Capitol Complex (Washington, U-Bahn-Station Kröpcke (Hannover, Germany) USE United States Highway 44 D.C.) USE U-Bahnhof Kröpcke (Hannover, Germany) U.S. 50 U.S. Cleveland Post Office Building (Punta Gorda, Fla.) U-Bahnhof Kröpcke (Hannover, Germany) USE United States Highway 50 UF Cleveland Post Office Building (Punta Gorda, UF Kröpcke, U-Bahnhof (Hannover, Germany) U.S. 51 Fla.) Station Kröpcke (Hannover, Germany) USE United States Highway 51 BT Post office buildings—Florida U-Bahn-Station Kröpcke (Hannover, Germany) U.S. 52 U.S. Coast Guard Light Station (Jupiter Inlet, Fla.) BT Subway stations—Germany USE United States Highway 52 USE Jupiter Inlet Light (Fla.) U-Bahnhof Lohring (Bochum, Germany) U.S. -

LCSH Section O
O, Inspector (Fictitious character) O-erh-kʾun Ho (Mongolia) O-wee-kay-no Indians USE Inspector O (Fictitious character) USE Orhon River (Mongolia) USE Oowekeeno Indians O,O-dimethyl S-phthalimidomethyl phosphorodithioate O-erh-kʾun River (Mongolia) O-wen-kʻo (Tribe) USE Phosmet USE Orhon River (Mongolia) USE Evenki (Asian people) O., Ophelia (Fictitious character) O-erh-to-ssu Basin (China) O-wen-kʻo language USE Ophelia O. (Fictitious character) USE Ordos Desert (China) USE Evenki language O/100 (Bomber) O-erh-to-ssu Desert (China) Ō-yama (Kanagawa-ken, Japan) USE Handley Page Type O (Bomber) USE Ordos Desert (China) USE Ōyama (Kanagawa-ken, Japan) O/400 (Bomber) O family (Not Subd Geog) O2 Arena (London, England) USE Handley Page Type O (Bomber) Ó Flannabhra family UF North Greenwich Arena (London, England) O and M instructors USE Flannery family BT Arenas—England USE Orientation and mobility instructors O.H. Ivie Reservoir (Tex.) O2 Ranch (Tex.) Ó Briain family UF Ivie Reservoir (Tex.) BT Ranches—Texas USE O'Brien family Stacy Reservoir (Tex.) OA (Disease) Ó Broin family BT Reservoirs—Texas USE Osteoarthritis USE Burns family O Hine Hukatere (N.Z.) OA-14 (Amphibian plane) O.C. Fisher Dam (Tex.) USE Franz Josef Glacier/Kā Roimata o Hine USE Grumman Widgeon (Amphibian plane) BT Dams—Texas Hukatere (N.Z.) Oa language O.C. Fisher Lake (Tex.) O-kee-pa (Religious ceremony) USE Pamoa language UF Culbertson Deal Reservoir (Tex.) BT Mandan dance Oab Luang National Park (Thailand) San Angelo Lake (Tex.) Mandan Indians—Rites and ceremonies USE ʻUtthayān hǣng Chāt ʻŌ̜p Lūang (Thailand) San Angelo Reservoir (Tex.) O.L. -

LCSH Section O
O, Inspector (Fictitious character) O-erh-kʾun Ho (Mongolia) O.T. Site (Wis.) USE Inspector O (Fictitious character) USE Orhon River (Mongolia) USE OT Site (Wis.) O,O-dimethyl S-phthalimidomethyl phosphorodithioate O-erh-kʾun River (Mongolia) O-wee-kay-no Indians USE Phosmet USE Orhon River (Mongolia) USE Oowekeeno Indians O., Ophelia (Fictitious character) O-erh-to-ssu Basin (China) O-wen-kʻo (Tribe) USE Ophelia O. (Fictitious character) USE Ordos Desert (China) USE Evenki (Asian people) O/100 (Bomber) O-erh-to-ssu Desert (China) O-wen-kʻo language USE Handley Page Type O (Bomber) USE Ordos Desert (China) USE Evenki language O/400 (Bomber) O family (Not Subd Geog) Ō-yama (Kanagawa-ken, Japan) USE Handley Page Type O (Bomber) Ó Flannabhra family USE Ōyama (Kanagawa-ken, Japan) O and M instructors USE Flannery family O2 Arena (London, England) USE Orientation and mobility instructors O.H. Ivie Reservoir (Tex.) UF North Greenwich Arena (London, England) Ó Briain family UF Ivie Reservoir (Tex.) BT Arenas—England USE O'Brien family Stacy Reservoir (Tex.) O2 Ranch (Tex.) Ó Broin family BT Reservoirs—Texas BT Ranches—Texas USE Burns family O Hine Hukatere (N.Z.) OA (Disease) O.C. Fisher Dam (Tex.) USE Franz Josef Glacier/Kā Roimata o Hine USE Osteoarthritis BT Dams—Texas Hukatere (N.Z.) OA-14 (Amphibian plane) O.C. Fisher Lake (Tex.) O.K. (The English word) USE Grumman Widgeon (Amphibian plane) UF Culbertson Deal Reservoir (Tex.) USE Okay (The English word) Oa language San Angelo Lake (Tex.) O-kee-pa (Religious ceremony) USE Pamoa language San Angelo Reservoir (Tex.) BT Mandan dance Oab Luang National Park (Thailand) BT Lakes—Texas Mandan Indians—Rites and ceremonies USE ʻUtthayān hǣng Chāt ʻŌ̜p Lūang (Thailand) Reservoirs—Texas O.L. -
U.S. Fish & Wildlife Service Proposed Boundary Notice of Availability: John H. Chafee Coastal Barrier Resources System (CBRS
U.S. Fish & Wildlife Service John H. Chafee Coastal Barrier Resources System (CBRS) Unit C00, Clark Pond, Massachusetts Summary of Proposed Changes Type of Unit: System Unit County: Essex Congressional District: 6 Existing Map: The existing CBRS map depicting this unit is: ■ 025 dated October 24, 1990 Proposed Boundary Notice of Availability: The U.S. Fish & Wildlife Service (Service) opened a public comment period on the proposed changes to Unit C00 via Federal Register notice. The Federal Register notice and the proposed boundary (accessible through the CBRS Projects Mapper) are available on the Service’s website at www.fws.gov/cbra. Establishment of Unit: The Coastal Barrier Resources Act (Pub. L. 97-348), enacted on October 18, 1982 (47 FR 52388), originally established Unit C00. Historical Changes: The CBRS map for this unit has been modified by the following legislative and/or administrative actions: ■ Coastal Barrier Improvement Act (Pub. L. 101-591) enacted on November 16, 1990 (56 FR 26304) For additional information on historical legislative and administrative actions that have affected the CBRS, see: https://www.fws.gov/cbra/Historical-Changes-to-CBRA.html. Proposed Changes: The proposed changes to Unit C00 are described below. Proposed Removals: ■ One structure and undeveloped fastland near Rantoul Pond along Fox Creek Road ■ Four structures and undeveloped fastland located to the north of Argilla Road and east of Fox Creek Proposed Additions: ■ Undeveloped fastland and associated aquatic habitat along Treadwell Island Creek,