Higher Order Information Identifies Tie Strength
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Girl Names Registered in 1996
Baby Girl Names Registered in 1996 # Baby Girl Names # Baby Girl Names # Baby Girl Names 1 Aaliyah 1 Aiesha 1 Aleeta 1 Aamino 2 Aileen 1 Aleigha 1 Aamna 1 Ailish 2 Aleksandra 1 Aanchal 1 Ailsa 3 Alena 2 Aaryn 4 Aimee 1 Alesha 1 Aashna 1Ainslay 1 Alesia 5 Abbey 1Ainsleigh 1 Alesian 1 Abbi 4Ainsley 6 Alessandra 3 Abbie 1 Airianna 1 Alessia 2 Abbigail 1Airyn 1 Aleta 19 Abby 4 Aisha 5 Alex 1 Abear 1 Aishling 25 Alexa 1 Abena 6 Aislinn 1 Alexander 1 Abigael 1 Aiyana-Marie 128 Alexandra 32 Abigail 2Aja 2 Alexandrea 5 Abigayle 1 Ajdina 29 Alexandria 2 Abir 1 Ajsha 5 Alexia 1 Abrianna 1 Akasha 49 Alexis 1 Abrinna 1Akayla 1 Alexsandra 1 Abyen 2Akaysha 1 Alexus 1 Abygail 1Akelyn 2 Ali 2 Acacia 1 Akosua 7 Alia 1 Accacca 1 Aksana 1 Aliah 1 Ada 1 Akshpreet 1 Alice 1 Adalaine 1 Alabama 38 Alicia 1 Adan 2 Alaina 1 Alicja 1 Adanna 1 Alainah 1 Alicyn 1 Adara 20 Alana 4 Alida 1 Adarah 1 Alanah 2 Aliesha 1 Addisyn 1 Alanda 1 Alifa 1 Adele 1 Alandra 2 Alina 2 Adelle 12 Alanna 1 Aline 1 Adetola 6 Alannah 1 Alinna 1 Adrey 2 Alannis 4 Alisa 1 Adria 1Alara 1 Alisan 9 Adriana 1 Alasha 1 Alisar 6 Adrianna 2 Alaura 23 Alisha 1 Adrianne 1 Alaxandria 2 Alishia 1 Adrien 1 Alayna 1 Alisia 9 Adrienne 1 Alaynna 23 Alison 1 Aerial 1 Alayssia 9 Alissa 1 Aeriel 1 Alberta 1 Alissah 1 Afrika 1 Albertina 1 Alita 4 Aganetha 1 Alea 3 Alix 4 Agatha 2 Aleah 1 Alixandra 2 Agnes 4 Aleasha 4 Aliya 1 Ahmarie 1 Aleashea 1 Aliza 1 Ahnika 7Alecia 1 Allana 2 Aidan 2 Aleena 1 Allannha 1 Aiden 1 Aleeshya 1 Alleah Baby Girl Names Registered in 1996 Page 2 of 28 January, 2006 # Baby Girl Names -

Baby Girl Names Registered in 2012
Page 1 of 49 Baby Girl Names Registered in 2012 # Baby Girl Names # Baby Girl Names # Baby Girl Names 1 Aadhira 1 Abbey-Gail 1 Adaeze 3 Aadhya 1 Abbi 2 Adah 1 Aadya 1 Abbie 1 Adaira 1 Aahliah 11 Abbigail 1 Adaisa 1 Aahna 1 Abbigaile 1 Adalayde 1 Aaira 2 Abbigale 3 Adalee 1 Aaiza 1 Abbigayle 1 Adaleigh 1 Aalaa 1 Abbilene 2 Adalia 1 Aaleah 1 Abbrianna 1 Adalie 1 Aaleya 20 Abby 1 Adalina 1 Aalia 8 Abbygail 1 Adalind 1 Aaliah 1 Abbygail-Claire 2 Adaline 33 Aaliyah 1 Abbygaile 8 Adalyn 1 Aaliyah-Faith 3 Abbygale 1 Adalyne 1 Aaliyah-noor 1 Abbygayle 10 Adalynn 1 Aamina 1 Abby-lynn 1 Adanaya 1 Aaminah 1 Abebaye 2 Adara 1 Aaneya 2 Abeeha 1 Adau 1 Aangi 1 Abeer 2 Adaya 1 Aaniya 2 Abeera 1 Adayah 2 Aanya 1 Abegail 1 Addaline 3 Aaralyn 1 Abella 1 Addalyn 2 Aaria 1 Abem 1 Addalynn 3 Aarna 1 Abeni 1 Addeline 1 Aarohi 2 Abheri 1 Addelynn 1 Aarolyn 1 Abida 3 Addie 1 Aarvi 1 Abidaille 1 Addie-Mae 2 Aarya 1 Abigael 3 Addilyn 1 Aaryana 159 Abigail 2 Addilynn 1 Aasha 1 Abigaile 1 Addi-Lynne 2 Aashi 3 Abigale 78 Addison 1 Aashka 1 Abigayl 13 Addisyn 1 Aashna 2 Abigayle 1 Addley 1 Aasiyah 1 Abijot 1 Addy 1 Aauriah 1 Abilleh 9 Addyson 1 Aavya 1 Abinoor 1 Adedamisola 1 Aayah 2 Abrianna 1 Adeena 1 Aayana 2 Abrielle 1 Adela 1 Aayat 2 Abuk 1 Adelade 2 Aayla 1 Abyan 1 Adelae 1 Aayushi 3 Abygail 14 Adelaide 1 Ababya 2 Abygale 1 Adelaide-Lucille 1 Abagail 1 Acacia 2 Adelaine 1 Abagayle 1 Acasia 17 Adele 1 Abaigael 2 Acelyn 1 Adeleah 1 Abba 1 Achan 1 Adelee 1 Abbagail 2 Achol 1 Adeleigh 1 Abbegail 1 Achsa 1 Adeleine 12 Abbey 11 Ada 2 Adelia Page 2 of 49 Baby Girl -

FALL COMMENCEMENT 2020 CELEBRATING the GRADUATING CLASS So Enter That Daily Thou Mayest Grow in Knowledge Wisdom and Love
FALL COMMENCEMENT 2020 CELEBRATING THE GRADUATING CLASS So enter that daily thou mayest grow in knowledge wisdom and love. To the Class of 2020, Congratulations on your graduation from Ohio University! You are one of the fortunate who has experienced the nation’s best transformative learning experience. This year has not been what any of us had planned, as the COVID-19 global pandemic changed all of our lives. I want to thank you for boldly responding to these historic changes by continuing to learn together, work together and support one another. You have shown great resilience as you navigated the many challenges of 2020 and I am very proud of you. Your class is truly special and will always be remembered at Ohio University for your spirit and fortitude. Your time at Ohio University prepared you for your future, and now you and your classmates are beginning your careers, advancing in new academic programs or taking on other challenges. I want you to know, though, that your transformation is not yet complete. For a true education does not stop with a diploma; it continues throughout every day of your life. I encourage you to take the lessons you have learned at Ohio University and expand upon them in the years to come. As you have already learned, the OHIO alumni network is a vast enterprise – accomplished in their respectable professions, loyal to their alma mater, and always willing to help a fellow Bobcat land that next job or find an apartment/realtor in a new city. I urge you to seek out your nearest alumni chapter or a special interest society of alumni and friends, to reach out through social media (#ohioalumni), and to stay connected to Ohio University. -

N O R Th Car O Lina Go Lf Busin
President’s Message March 2019 When you are at a gathering of folks you don’t know, what do you talk about? The weather, of course. Well unfortunately that topic remains pervasive among golf course owners and operators. And save a couple of short-term exceptions, our weather could not be worse. Again we are way ahead on precipitation and we can’t catch a break to capture much revenue. You would think that roulette ball would land on a black number after 10 straight red numbers! As golf course owners and operators, it is critical that we have a business and political climate that is fair and balanced in allowing us to operate our courses. Today’s political landscape is challenging to say the least, and our goal is to make sure that our elected officials are informed about our industry, so they can make good decisions when they involve the business that is our livelihood. Golf not only supports us and our families, it is crucial to our fellow workers, employees and millions of Americans that enjoy the fun and healthy experience of golf. To this end, I will be traveling on May 1 of this year with our Executive Golf Golf Director David Norman to Washington, DC for National Golf Day. We will join a group of hundreds of members of the golf community in our continuing effort to provide relevant information to the members of Congress that form the backbone of our governing process. But as we lament, it’s time to make our own luck. -

Search the List of Unclaimed Child Support
UNCLAIMED CHILD SUPPORT AS OF 02/08/2021 TO RECEIVE A PAPER CLAIM FORM, PLEASE CALL WI SCTF @ 1-800-991-5530. LAST NAME FIRST NAME MI ADDRESS CITY ABADIA CARMEN Y HOUSE A4 CEIBA ABARCA PAULA 7122 W OKANOGAN PLACE BLDG A KENNEWICK ABBOTT DONALD W 11600 ADENMOOR AVE DOWNEY ABERNATHY JACQUELINE 7722 W CONGRESS MILWAUKEE ABRAHAM PATRICIA 875 MILWAUKEE RD BELOIT ABREGO GERARDO A 1741 S 32ND ST MILWAUKEE ABUTIN MARY ANN P 1124 GRAND AVE WAUKEGAN ACATITLA JESUS 925 S 14TH ST SHEBOYGAN ACEVEDO ANIBAL 1409 POSEY AVE BESSEMER ACEVEDO MARIA G 1702 W FOREST HOME AVE MILWAUKEE ACEVEDO-VELAZQUEZ HUGO 119 S FRONT ST DORCHESTER ACKERMAN DIANE G 1939 N PORT WASHINGTON RD GRAFTON ACKERSON SHIRLEY K ADDRESS UNKNOWN MILWAUKEE ACOSTA CELIA C 5812 W MITCHELL ST MILWAUKEE ACOSTA CHRISTIAN 1842 ELDORADO DR APT 2 GREEN BAY ACOSTA JOE E 2820 W WELLS ST MILWAUKEE ACUNA ADRIAN R 2804 DUBARRY DR GAUTIER ADAMS ALIDA 4504 W 27TH AVE PINE BLUFF ADAMS EDIE 1915A N 21ST ST MILWAUKEE ADAMS EDWARD J 817 MELVIN AVE RACINE ADAMS GREGORY 7145 BENNETT AVE S CHICAGO ADAMS JAMES 3306 W WELLS ST MILWAUKEE ADAMS LINDA F 1945 LOCKPORT ST NIAGARA FALLS ADAMS MARNEAN 3641 N 3RD ST MILWAUKEE ADAMS NATHAN 323 LAWN ST HARTLAND ADAMS RUDOLPH PO BOX 200 FOX LAKE ADAMS TRACEY 104 WILDWOOD TER KOSCIUSKO ADAMS TRACEY 137 CONNER RD KOSCIUSKO ADAMS VIOLA K 2465 N 8TH ST LOWER MILWAUKEE ADCOCK MICHAEL D 1340 22ND AVE S #12 WIS RAPIDS ADKISSON PATRICIA L 1325 W WILSON AVE APT 1206 CHICAGO AGEE PHYLLIS N 2841 W HIGHLAND BLVD MILWAUKEE AGRON ANGEL M 3141 S 48TH ST MILWAUKEE AGUILAR GALINDO MAURICIO 110 A INDUSTRIAL DR BEAVER DAM AGUILAR SOLORZANO DARWIN A 113 MAIN ST CASCO AGUSTIN-LOPEZ LORENZO 1109A S 26TH ST MANITOWOC AKBAR THELMA M ADDRESS UNKNOWN JEFFERSON CITY ALANIS-LUNA MARIA M 2515 S 6TH STREET MILWAUKEE ALBAO LORALEI 11040 W WILDWOOD LN WEST ALLIS ALBERT (PAULIN) SHARON 5645 REGENCY HILLS DRIVE MOUNT PLEASANT ALBINO NORMA I 1710 S CHURCH ST #2 ALLENTOWN Page 1 of 138 UNCLAIMED CHILD SUPPORT AS OF 02/08/2021 TO RECEIVE A PAPER CLAIM FORM, PLEASE CALL WI SCTF @ 1-800-991-5530. -
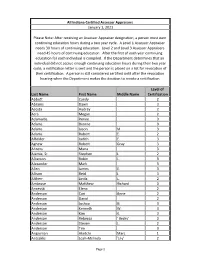
Last Name First Name Middle Name Level of Certification Abbott Candy
All Indiana Certified Assessor Appraisers January 1, 2021 Please Note: After receiving an Assessor Appraiser designation, a person must earn continuing education hours during a two year cycle. A Level 1 Assessor Appraiser needs 30 hours of continuing education. Level 2 and Level 3 Assessor Appraisers need 45 hours of continuing education. After the first of each year continuing education for each individual is compiled. If the Department determines that an individual did not accrue enough continuing education hours during their two year cycle, a notification letter is sent and the person is placed on a list for revocation of their certification. A person is still considered certified until after the revocation hearing when the Department makes the decision to revoke a certification. Level of Last Name First Name Middle Name Certification Abbott Candy 2 Abrams Dawn 3 Acosta Audrey 2 Acra Megan 2 Adamaitis Renee 3 Adams Dionne 3 Adams Jason M. 3 Adams Robert E. 2 Affolder Judith E. 3 Agnew Robert Gray 3 Ahrens Muna 3 Ajamie, Sr. Stephen J. 2 Alberson Robin L. 3 Alexander Mark 3 Allen James E. 3 Allison Reid J. 3 Altherr Linda L. 2 Ambrose Matthew Richard 3 Ancevski Elena 2 Anderson Cori Anne 2 Anderson David 2 Anderson Joshua G. 3 Anderson Kenneth W. 3 Anderson Kim K. 3 Anderson Rebecca ' Becky' 3 Anderson Steven L. 2 Anderson Tim 3 Angniman Aketchi Marc 1 Antsaklis Leah-Melinda 'Lily' 2 Page 1 Archer Joshua T. 2 Archer Richard L. 3 Arion Sandy 2 Armbruster Dale 3 Arnold Kelli 3 Arocho Millie 3 Atkinson Benjamin 2 Aubrey Jennifer ' Jeni' 3 Austgen John K. -

Conroe Warrant Listing Municipal Court Current As of 03/28/2019
Conroe Warrant Listing Municipal Court Current as of 03/28/2019 Name Warrant # Amount Due DUSHA III, ALAN BRUCE MICHAEL 174416831 SPEEDING 62 MPH in a 50 MPH Zone $105.00 # Of Warrants: 1 Amount Due: $105.00 ABADALLAH, KAWAR SAMI 15030077 CAMPING IN PUBLIC OR PRIVATE AREAS PROHIBITED $416.00 15030077W FAIL TO APPEAR $416.00 # Of Warrants: 2 Amount Due: $832.00 ABARCA, ALLAN OSMAN 174804441 SPEEDING 57 MPH in a 45 MPH Zone $278.10 174804442 NO DRIVERS LICENSE $300.00 17480444W1 VIOLATE PROMISE TO APPEAR $383.00 # Of Warrants: 3 Amount Due: $961.10 ABBOTT, DARRELL EVERETTE 175606151 FAIL TO RESTRAIN YOUNGER THAN 8 OR LESSTHAN 4'9"-DRIVER $302.00 17560615W1 VIOLATE PROMISE TO APPEAR $383.00 # Of Warrants: 2 Amount Due: $685.00 ABBOTT, MICHAEL RAY 12320453 SPEEDING 64 MPH in a 45 MPH Zone $449.93 12320453 FMFR 2ND OFFENSE $690.30 12320453 DRIVING WHILE LICENSE INVALID $452.40 12320453W VIOLATE PROMISE TO APPEAR $495.30 # Of Warrants: 4 Amount Due: $2,087.93 ABBOTT, TIMOTHY MARK 12480555 POSSESSION OF DRUG PARAPHERNALIA $413.40 12480555W FAIL TO APPEAR $452.40 # Of Warrants: 2 Amount Due: $865.80 ABBOTT, ZACHARY ATOM 179503061 DRIVING WHILE LICENSE INVALID $350.00 17950306W1 VIOLATE PROMISE TO APPEAR $383.00 # Of Warrants: 2 Amount Due: $733.00 ABBS, CHRISTOPHER DEMONTROND RAY 3482631 CROSS ROAD OUTSIDE CROSSWALK $213.00 348263W1 VIOLATE PROMISE TO APPEAR $497.90 # Of Warrants: 2 Amount Due: $710.90 ABDULLAHI, HALIMAH SADIA 12420260 UNSAFE LANE CHANGE $427.18 12420260 NO DRIVERS LICENSE $384.28 12420260W VIOLATE PROMISE TO APPEAR $456.30 # -

Last Name First Name Birth Yrfather's Last Name Father's
Last Name First Name Birth YrFather's Last Name Father's First Name Mother's Last Name Mother's First Name Gender Aaron 1907 Aaron Benjaman Shields Minnie M Aaslund 1893 Aaslund Ole Johnson Augusta M Aaslund (Twins) 1895 Aaslund Oluf Carlson Augusta F Abbeal 1906 Abbeal William A Conlee Nina E M Abbitz Bertha Dora 1896 Abbitz Albert Keller Caroline F Abbot 1905 Abbot Earl R Seldorff Rose F Abbott Zella 1891 Abbott James H Perry Lissie F Abbott 1896 Abbott Marion Forder Charolotta M M Abbott 1904 Abbott Earl R Van Horn Rose M Abbott 1906 Abbott Earl R Silsdorff Rose M Abercrombie 1899 Abercrombie W Rogers A F Abernathy Marjorie May 1907 Abernathy Elmer Scott Margaret F Abernathy 1892 Abernathy Wm A Roberts Laura J F Abernethy 1905 Abernethy Elmer R Scott Margaret M M Abikz Louisa E 1902 Abikz Albert Keller Caroline F Abilz Charles 1903 Abilz Albert Keller Caroline M Abircombie 1901 Abircombie W A Racher Allos F Abitz Arthur Carl 1899 Abitz Albert Keller Caroline M Abrams 1902 Abrams L E Baker May F Absher 1905 Absher Ben Spillman Zoida M Achermann Bernadine W 1904 Ackermann Arthur Krone Karolina F Acker 1903 Acker Louis Carr Lena F Acker 1907 Acker Leyland Ryan Beatrice M Ackerman 1904 Ackerman Cecil Addison Willis Bessie May F Ackermann Berwyn 1905 Ackermann Max Mann Dolly M Acklengton 1892 Achlengton A A Riacting Nattie F Acton Rebecca Elizabeth 1891 Acton T M Cox Josie E F Acton 1900 Acton Chas Payne Minnie M Adair Elles 1906 Adair Adel M Last Name First Name Birth YrFather's Last Name Father's First Name Mother's Last Name Mother's -

Nurse Aide Employment Roster Report Run Date: 9/24/2021
Nurse Aide Employment Roster Report Run Date: 9/24/2021 EMPLOYER NAME and ADDRESS REGISTRATION EMPLOYMENT EMPLOYMENT EMPLOYEE NAME NUMBER START DATE TERMINATION DATE Gold Crest Retirement Center (Nursing Support) Name of Contact Person: ________________________ Phone #: ________________________ 200 Levi Lane Email address: ________________________ Adams NE 68301 Bailey, Courtney Ann 147577 5/27/2021 Barnard-Dorn, Stacey Danelle 8268 12/28/2016 Beebe, Camryn 144138 7/31/2020 Bloomer, Candace Rae 120283 10/23/2020 Carel, Case 144955 6/3/2020 Cramer, Melanie G 4069 6/4/1991 Cruz, Erika Isidra 131489 12/17/2019 Dorn, Amber 149792 7/4/2021 Ehmen, Michele R 55862 6/26/2002 Geiger, Teresa Nanette 58346 1/27/2020 Gonzalez, Maria M 51192 8/18/2011 Harris, Jeanette A 8199 12/9/1992 Hixson, Deborah Ruth 5152 9/21/2021 Jantzen, Janie M 1944 2/23/1990 Knipe, Michael William 127395 5/27/2021 Krauter, Cortney Jean 119526 1/27/2020 Little, Colette R 1010 5/7/1984 Maguire, Erin Renee 45579 7/5/2012 McCubbin, Annah K 101369 10/17/2013 McCubbin, Annah K 3087 10/17/2013 McDonald, Haleigh Dawnn 142565 9/16/2020 Neemann, Hayley Marie 146244 1/17/2021 Otto, Kailey 144211 8/27/2020 Otto, Kathryn T 1941 11/27/1984 Parrott, Chelsie Lea 147496 9/10/2021 Pressler, Lindsey Marie 138089 9/9/2020 Ray, Jessica 103387 1/26/2021 Rodriquez, Jordan Marie 131492 1/17/2020 Ruyle, Grace Taylor 144046 7/27/2020 Shera, Hannah 144421 8/13/2021 Shirley, Stacy Marie 51890 5/30/2012 Smith, Belinda Sue 44886 5/27/2021 Valles, Ruby 146245 6/9/2021 Waters, Susan Kathy Alice 91274 8/15/2019 -
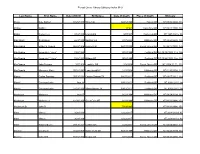
Obituary Index.Xlsx
Forest Grove Library Obituary Index M-O Last Name First Name Date of Birth Birthplace Date of Death Place of Death Obituary Maag Dale Delbert 07/25/1910 Wray CO 04/26/1998 Tigard OR NT 05/06/1998, 17a Mabon Wallace c1961 Coos Bay OR NT 06/21/2000, 18a Mabry Denver Lee 8/14/1913 Lincoln KS 9/7/1987 Cornelius OR NT 1987-09-16, 8A Mac Intosh Scott Osen 6/23/1950 Hanford CA 8/17/2000 Hillsboro OR NT 08/23/2000, 18a MacDonald Esther B Powers 06/22/1906 Denver CO 06/13/1998 Forest Grove OR NT 06/17/1998, 17a MacDonald Jeremiah F "Jerry" 7/22/1923 9/12/1999 Portland OR NT 09/15/1999, 11a, 12a MacDonald Jeremiah F "Jerry" 7/22/1923 Billings MT 9/12/1999 Portland OR NT 09/22/1999, 18a, 19a MacDonald John Bertram 5/7/1906 Leadville CO 2/8/2004 Forest Grove OR NT 2004-02-11, 11A MacDonald Maryanne Marie 05/01/1941 Long Island NY 1/23/2008 Hillsboro OR NT 01/30/2008, 12a Maciel Carlos Sanchez 05/13/1936 Carrizo Springs TX 08/27/2011 Portland OR NT 09/07/2011, 11a Maciel Dominga Lydia Age 75 09/12/2011 Portland OR NT 09/14/2011, 9a Maciel Dominga Lydia 02/23/1936 Winter Haven TX 09/12/2011 Portland OR NT 09/21/2011, 9a MacIntosh Marianne Age 67 8/22/1994 Hillsboro OR NT 08/24/1994, 11a MacIntosh Marianne A 12/26/1926 Great Falls MT 8/22/1994 Hillsboro OR NT 08/31/1994, 15A MacIntosh Sr John D 7/19/1985 NT 08/31/1994, 15A Mack Mary C 3/28/1919 12/22/2017 NT 2018-01-03, A5 Mack Mary C 3/28/1919 12/22/2017 NT 2018-01-10, A8 Mack Raymond Lee 08/13/1924 Guthrie OK 5/29/2007 Forest Grove OR NT 06/06/2007, 17a Mackey Dorothy B 01/22/1909 Myrtle Point OR -

CV 0019 District Civil Family Docket Book.Rdl
CIVIL SETTINGS FOR DISTRICT COURT ON Monday, October 04, 2021, 09:00 AM JURY CIVIL SETTINGS FOR DISTRICT COURT ON Monday, October 04, 2021, 09:00 AM JURY 1 D-1-AG-11-002097 TEXAS DEPARTMENT OF FAMILY AND PROTECTIVE SERVICES vs. SAVANNAH LEE ANNAS 5.00 Days Set By PLAINTIFF JURY 1 Atty PAUL HILL 1 Atty ROBYNN FLETCHER 1 Atty KAREEM MCCULLEY 2 Atty ELIZABETH SCHWARTZ 2 D-1-FM-19-006668 TEXAS DEPARTMENT OF FAMILY AND PROTECTIVE SERVICES vs. SAVANNAH LEE ANNAS 5.00 Days Set By PLAINTIFF JURY 1 Atty PAUL HILL 1 Atty ROBYNN FLETCHER 1 Atty KAREEM MCCULLEY 2 Atty COLIN GAFFNEY 3 D-1-GN-20-000222 JUAN WONG vs. JESUS DIAZ 5.00 Days Set By PLAINTIFF JURY 1 Atty CARL BROOKS SCHUELKE 1 Atty JOSEPH MATTHEW CROSS 2 Atty CARL BROOKS SCHUELKE 2 Atty JOSEPH MATTHEW CROSS 3 Atty ADAM WYMA 4 D-1-GN-20-002895 MICHAEL CONNELL vs. SUNGJUN YOON 3.00 Days Set By DEFENDANT JURY 1 Atty MICHAEL BURKE 1 Atty CATHERINE MARSOLAN 1 Atty PRINCESS CAMPOS 1 Atty CASSANDRA CORREA 5 D-1-GN-18-000196 JUAN URQUIZA vs. ANDREW FAUD DUNA 4.00 Days Set By PLAINTIFF JURY 1 Atty ANDREW SAUL TRAUB 1 Atty MICAH WILLIAMS 6 D-1-GN-18-003355 CARLOS CAMPOS vs. CAPITAL PUMPING LP 5.00 Days Set By PLAINTIFF JURY 1 Atty ROBERT MICHAEL MELENDEZ 1 Atty MICHAEL KIRKLAND 2 Atty ROBERT MICHAEL MELENDEZ 2 Atty MICHAEL KIRKLAND 3 Atty CHARLES JOSEPH CAIN 8 D-1-GN-20-000030 JIMMY ORNELAS vs. -

Executive Branch
EXECUTIVE BRANCH EXECUTIVE OFFICE OF THE PRESIDENT Type Level, Location Position Name of Incumbent of Pay Grade, or Tenure Expires Appt. Plan Pay EXECUTIVE OFFICE OF THE PRESIDENT WHITE HOUSE OFFICE Washington, DC .... Assistant to the President and Chief of Staff Jacob J. Lew ....................... PA AD ................ ................ Do .................... Assistant to the President for Homeland Se- John O. Brennan ................ PA AD ................ ................ curity and Counterterrorism. Do .................... Assistant to the President and Press Sec- James F. Carney ................ PA AD ................ ................ retary. Do .................... Assistant to the President and Deputy Chief Mark B. Childress .............. PA AD ................ ................ of Staff for Planning. Do .................... Assistant to the President and Deputy Chief Nancy-Ann M. DeParle ...... PA AD ................ ................ of Staff for Policy. Do .................... Assistant to the President and National Secu- Thomas E. Donilon ............ PA AD ................ ................ rity Advisor. Do .................... Assistant to the President and Director of Jonathan E. Favreau ......... PA AD ................ ................ Speechwriting. Do .................... Assistant to the President and Deputy Na- Michael B. Froman ............ PA AD ................ ................ tional Security Advisor for International Economics. Do .................... Senior Advisor and Assistant to the President Valerie B. Jarrett